AUTOMATIC APPROACH FOR RECTIFYING BUILDING

FACADES FROM A SINGLE UNCALIBRATED IMAGE

Wenting Duan and Nigel M. Allinson

The Department of Electronic and Electrical Engineering, The University of Sheffield

Mappin Street, Sheffield, U.K.

Keywords: Facade rectification, Vanishing point estimation, Line grouping, Building recognition.

Abstract: We describe a robust method for automatically rectifying the main facades of buildings from single images

taken from short to medium distances. This utility is an important step in building recognition,

photogrammetry and other 3D reconstruction applications. Our main contribution lies in a refinement

technique for vanishing point estimation and building line grouping, since both significantly affect the

location and warping of building facades. The method has been shown to work successfully on 96% of

images from the Zubud-Zurich building database where images frequently contain occlusions, different

illumination conditions and wide variations in viewpoint.

1 INTRODUCTION

The rectification of main building facades to their

fronto-parallel view is of importance in building

recognition, photogrammetry and other 3D

reconstruction applications (Wang et al., 2005). It

can simplify the extraction of metric information and

recover the canonical shape of a building because

the metric rectification allows the scene to be

warped-back using a similarity transformation. In

other words, the rectified view is almost free from

perspective distortion. It should be noted that the

rectification problem addressed here is different

from image rectification for stereo vision, where the

purpose is to match the epipolar projections of

image pairs (Hartley, 1999). How to rectify a single

uncalibrated image is a different challenge; and

various approaches having been proposed and

studied.

As pointed out by Menudet et al. (2008),

“camera self-calibration is intrinsically related to

metric reconstruction”. Therefore, an important

factor for rectification lies in obtaining accurate

calibration parameters and inclusion of appropriate

scene constraints. Menudet et al. (2008) described a

new way of decomposing the scene-to-image

homography, which allows a cost function to assess

how close the rectification is to similarity. However,

to obtain the calibration parameters, at least four

images of the same scene were required. Using only

a single image of a particular scene, Liebowits and

Zisserman (1998) utilised some geometric

constraints such as equal angles for rectification.

Chen and Ip (2005) achieved rectification by using

the vanishing line and an arbitrary circle extracted

from the image to estimate the image of the absolute

conic (IAC). In the context of rectifying building

images, reliable geometric features such as parallel

lines and orthogonal angles can be used as scene

constraints (Hu, Sawyer and Herve, 2006; Robertson

and Cipolla, 2004; David, 2008; Košecká and Zhang,

2005). The estimation of the vanishing line is a

major technique to recover images from perspective

distortion. Hence, improving the accuracy and

efficiency of computing these vanishing points is of

foremost interest. Košecká and Zhang (2002)

proposed a technique of applying the EM algorithm

to detect vanishing points for images taken in

man-made environments. The method achieved

good accuracy with vanishing points being detected,

on average, within 5 pixels of their true position.

However, for building facade rectification, the

following factors can adversely affect the success

rate of detecting vanishing points. Firstly the images

of the building can be taken in different illumination

conditions and from different viewpoints. Secondly

occlusion and scene clutter can obscure the building

image. Finally, not all buildings have facades that

are orthogonal to each other. These issues have not

Duan W. and Allinson N. (2009).

AUTOMATIC APPROACH FOR RECTIFYING BUILDING FACADES FROM A SINGLE UNCALIBRATED IMAGE.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 37-43

DOI: 10.5220/0002191600370043

 SciTePress

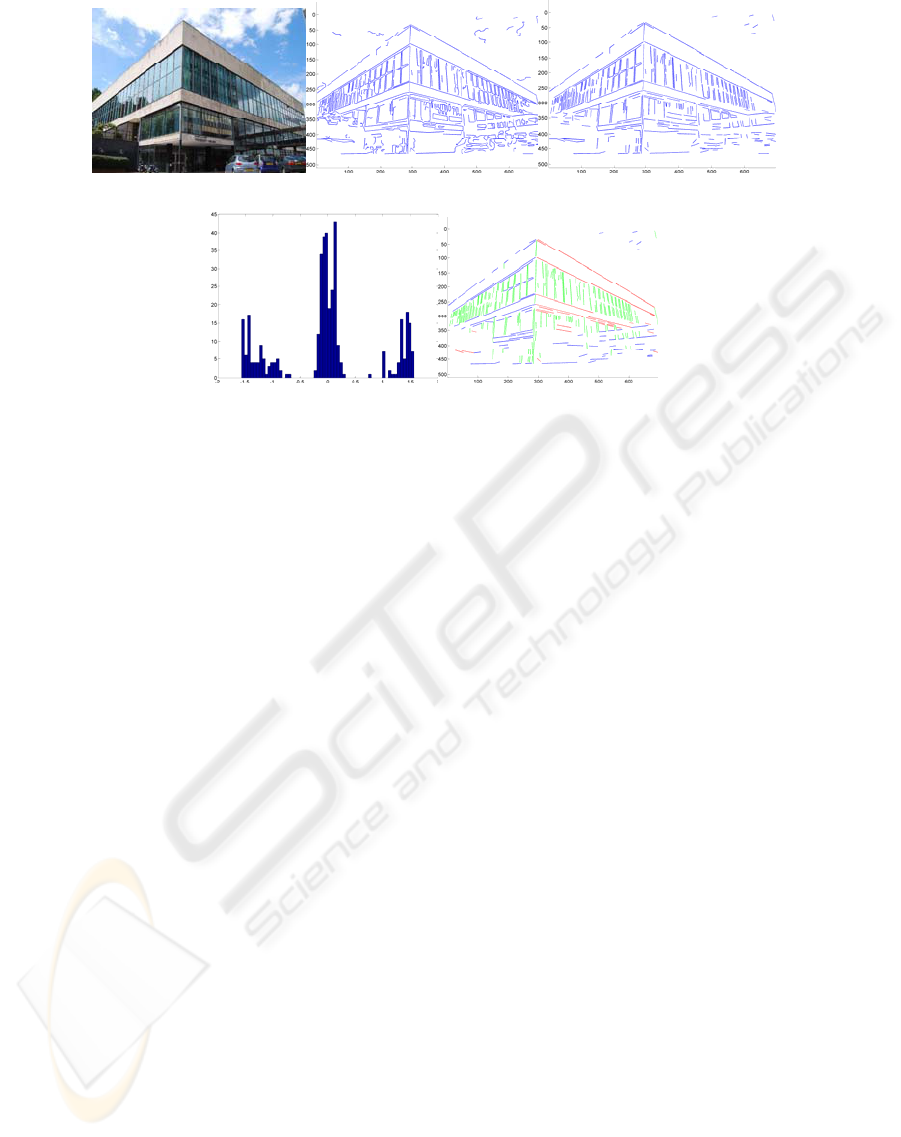
(a) (b) (c)

(d) (e)

Figure 1: (a) Original Image (700×468 pixels) – Main Library of Sheffield University; (b) Line segments fitted to the

connected edge points; (c) Line segments with length > 15 selected; (d) Histogram of line segment directions; (e) Separated

groups of line segments associated with the three principal directions.

been considered by existing methods for building

rectification, and for this reason it is desirable to

develop more robust methods that can handle these

potential problems.

In this paper, we first present a method based on

Expectation-Maximisation (EM) algorithm for

estimating the vanishing points of building images.

Then, we show how to use the appropriate scene

constraints appeared in the image to enable

automatic rectification of the main building facades.

The approach is described in Section 2. In Section 3,

the results are presented and compared to Košecká

and Zhang’s work (2002). Finally, we draw some

conclusions.

2 METHOD

2.1 Line Segments Detection and Initial

Grouping

Lines, derived from local intensity edges, in building

images contain significant and stable geometric

information because the majority are aligned to the

three principal axes. These three axes are associated

with the 3D orthogonal real-world axes. Under

perspective transformation, the parallel lines of

buildings intersect at vanishing points in the image

(though the actual vanishing points may be outside

the area of the captured scene). Hence, first of all,

we need to find those groups of lines that are

associated with these vanishing directions. A

conventional Canny edge detector was used to find

edge strength and orientation followed by

non-maximum suppression. Hysteresis thresholding

was then used to further refine the recovered edges.

We applied the edge-linking function (Kovesi,

2000-2006) to the detected edges to label connected

edge points. The linked points with a length under

15 pixels were discarded since these lengths were

determined experimentally to be inconsequential for

our image sizes (typically 700×468 pixels). A

line-fitting scheme was then utilised to form straight

line segments from these linked edges. At this stage,

a line segment list was produced, which contains the

end point coordinates of all the computed line

segments in the image coordinate frame. A typical

example is shown in Fig. 1(b).

In Fig. 1(b), we can easily see that most short

line segments belong to the background or general

scene clutter. The many short ones belonging to the

building are also not reliable. Hence, the length of

each segment was calculated and again ones longer

than 15 pixels were selected. This small step also

enables us to roughly segment the building region

from the whole scene (Fig. 1(c)). The directions of

all the lines were calculated in order to compute the

histogram shown in Fig. 1(d). The top peaks which

are at least five bins apart were selected after curve

fitting to the histogram. The lines which have

orientation within the range of +/-π/8 around a

particular peak were included in the same group.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

(a) (b) (c)

(d) (e) (f)

Figure 2: (a) Building with occlusion; (b) Detected and initially grouped two sets of lines for image (a); (c) Refined line

groups for (a); (d) Building with confusing line directions; (e) Two initial groups of lines for image (d) – left side of the

image contain lines that do not belong to the expected vanishing direction; (f) Refined line groups of (d).

The resultant three main groups are shown in Fig.

1(e) as separate colours.

For each group of line segments, we can now

compute their initial vanishing point. In Fig. 1(e),

each line segment is plotted by connecting their two

end points x

and x

. In a homogeneous form,

= (x

,1) and x

= (x

,1). Under the 2D

projective plane, the homogeneous line

representation is obtained by:

l = x

×x

(1)

As mentioned above, under perspective

transformations, parallel lines in the real-world

coordinate frame intersect at vanishing points in the

image plane. The two lines l

and l

intersect at the

point v = l

×l

. Alternatively, the relationship

between vanishing points and their associated lines

can be expressed as v

l = 0. However, with so many

pairs of lines available in each principal axis, we can

produce many differing vanishing points. This

requires us to solve the linear least square estimation

problem:

()

∑

min

(2)

where n is the number of lines. This formula (2) can

be written as

min

||Av||

(3)

The rows of matrix A are the grouped lines with

the same vanishing direction.

Before solving the linear least square estimation

problem, we need to normalise the image end-point

coordinates since we are dealing with the case of an

uncalibrated camera. More detailed information of

normalisation can be found in Košecká and Zhang

(2002). The initial vanishing point for each group

was calculated by the closed form solution of (3),

where the estimation of v was the eigenvector

associated with the smallest eigenvalue of A

A. The

initial grouping of lines and estimated vanishing

points are accurate enough for the example image in

Fig. 1(a). However, for images with occlusions or

false groupings such as in Fig. 2(a) and (b), further

refinement is necessary. For example, Fig. 2(a)

shows a building with some occlusions. Its initial

grouped lines (as shown in Fig. 2(b)) causes large

errors in vanishing point detection. The building in

Fig. 2(d) also contains lines that do not belong to the

dominant vanishing directions but are still grouped.

2.2 Further Refinement of Vanishing

Points Locations based on EM

Algorithm

The refinement method is based on the Expectation

Maximisation (EM) algorithm. We first compute the

likelihood of line segments l

belonging to each of

the initially estimated vanishing points v

by the

formula:

()

⎟

⎠

⎞

⎜

⎝

⎛

−

∝

exp)|(

vlp

(4)

AUTOMATIC APPROACH FOR RECTIFYING BUILDING FACADES FROM A SINGLE UNCALIBRATED IMAGE

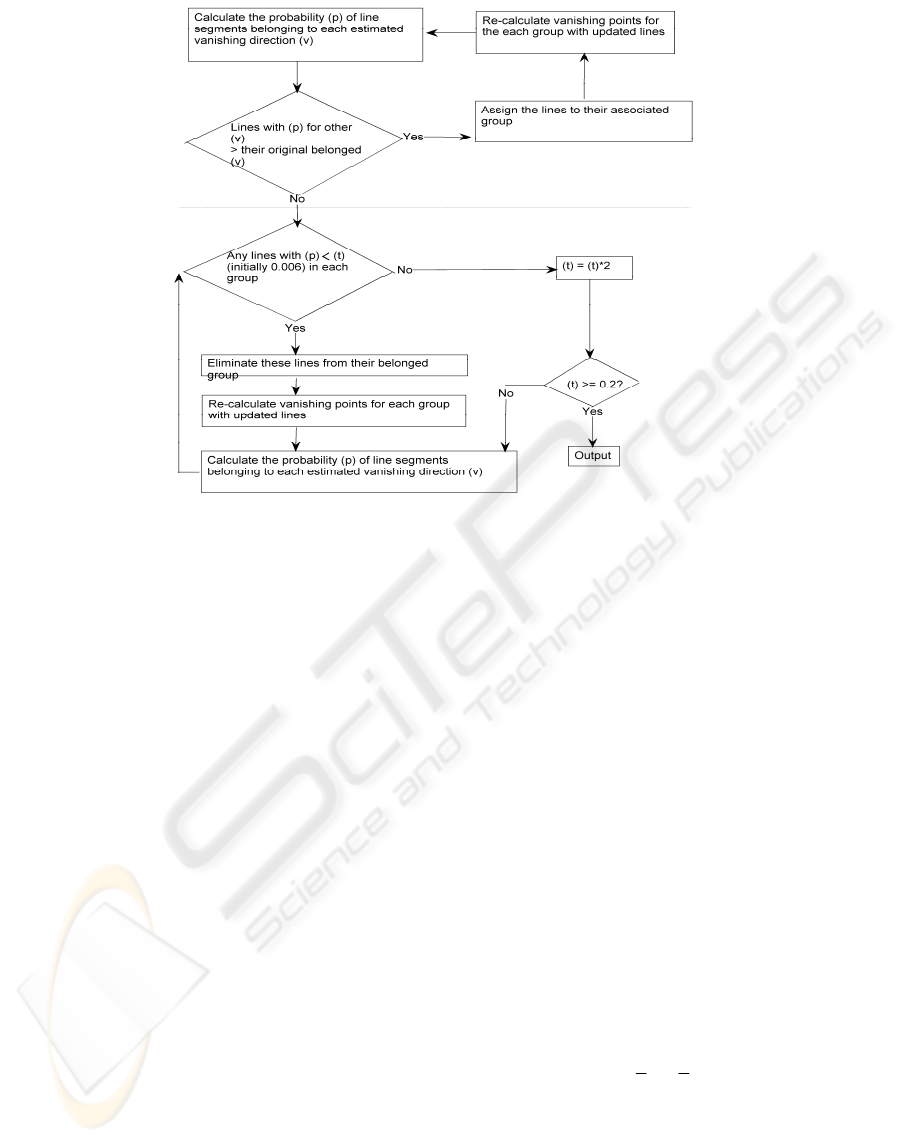
Figure 3: Flow chart of the refining process.

The upper half of the flow chart - Fig. 3 is

mainly used for re-grouping lines and combining

similar vanishing directions. The probabilities for

each line corresponded to every vanishing direction

were compared. The updated line groups were

passed to the lower half of the algorithm when no

lines are found to belong to other directions. The

lower half eliminates lines with low probability for

the direction they belong to so producing more

accurate estimates of vanishing point locations. The

iteration stops when line probabilities for each group

are all above 0.1. In our experiments, t = 0.1

normally is sufficient to give an accurate vanishing

point. The effect of this refining process for Fig. 2(a)

and (d) is shown in Fig.2(c) and (f).

2.3 Automatic Rectification of Main

Building Facades

To automatically warp an image’s main building

facades to the fronto-parallel view, we have to use

the geometric information provided by the image, no

external interaction should be required during the

processing. We followed the approach described by

Liebowitz and Zisserman (1998) as well as Hartley

and Zisserman （2003). Here, we briefly summarize

the method. The homography H which relates the

points x in the image plane to x’ （homogeneous

3-vector ） in the real-world plane can be

decomposed into three transformation matrices: H =

Similarity * Affine * Projective.

The first transformation is a pure projective

transformation obtained with the vanishing line of

the plane:

⎥

⎦

⎤

⎢

⎣

⎡

321

010

001

lll

(5)

where l

, l

and l

are the vector elements of the

vanishing line l

∞

. Since the vanishing line is

computed by the two vanishing points from their

corresponding facade, the vanishing point

corresponds to the vertical lines of the building

normally need to be used twice. For images with

three vanishing points, we decided the vertical

vanishing point by exploiting the location of the

coordinates of all vanishing points with respect to

the image’s principal point.

The affine transformation which enables the

recovery of metric geometry is expressed as:

⎟

⎠

⎞

⎜

⎝

⎛

−

100

010

(6)

where α and β are the two parameters involved in the

transformation of circular points from the metric

plane to the affine plane. When the metric geometry

is restored it includes angles and length ratios of

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

(a) (b) (c)

(d) (e) (f)

Figure 4: (a) Building with facades not aligned with the three orthogonal axes; (b) Initial grouping for image (a); (c)

Refined line groups for (b); (d) Image taken from a critical viewpoint; (e) Plenty of lines grouped falsely; (f) Refined line

groups for (e).

non-parallel line segments. In order to determine α

and β, two constraints for non-parallel line sets must

be supplied. The constraints can be obtained from “a

known angle between lines; Equality of two

(unknown) angles; and a known length ratio”

(Liebowitz and Zisserman, 1998). Each constraint

produces a circle in the complex plane with α and β

indeed its real and imaginary components. The value

of α and β can be found at the intersection points of

two circles. However, for the problem of building

facade rectification, there is only one constraint that

the detected line segments provide with high

confidence — the right angle between the two sets

of lines. Therefore, the parameter β is assumed to be

1. This assumption is based on the fact that under

affine transformations, the circular points with

coordinates

()

i 0,,1 ± in the metric plane are

mapped to

()

i 0,1,

βα

. If no affine distortion

occurred, the value of α and β is (0, 1)

The last similarity transformation matrix is in the

form of:

⎟

⎠

⎞

⎜

⎝

⎛

tsR

s and

⎟

⎠

⎞

⎜

⎝

⎛

−

θθ

cossin

sincos

R (7)

This final stage is used to: (i) adjust the image

centre so that no coordinates of the image points has

a negative value; (ii) rotate the line sets in order to

make sure the majority of the lines in each group are

aligned with the x and y axis directions; and (iii)

scale the image up or down if the warped image size

exceeds our desired value.

3 DISCUSSION

The approach proposed for building facade

rectification was tested on the buildings images from

the Zubud-Zurich buildings database (Shao and

Gool, 2003). The method managed to rectify 96% of

all the images tested. From this test, we found that

the key to properly warp the building facades lies in

the accuracy of the vanishing points and grouping of

real-world parallel lines. The proposed refinement

method was compared with Košecká and Zhang’s

(2002) work on vanishing points detection. Our

experiment shows following improvement in the

context of rectifying building images:

(1) Accuracy of Estimated Vanishing Points.

Instead of assigning probability weights to each line

for the Maximisation step described in [11], the lines

with very low probability to the vanishing point of

the associated group are eliminated or assigned to

other groups. Therefore, lines which could degrade

the estimate of vanishing point are reduced. From

our experiments, the average deviation of vanishing

points from its manually measured true position is

five pixels, (the true position was decided by using

AUTOMATIC APPROACH FOR RECTIFYING BUILDING FACADES FROM A SINGLE UNCALIBRATED IMAGE

Figure 5: Some example images with their associated warped facades.

Figure 6: Deviation errors from being parallel of the projective warped lines (for first three building examples in Fig.5) –

assessing vanishing point accuracy in each line set.

ruler to extend major building lines and locating the

intersection).

(2) Better Grouping of Lines. Buildings can have

facades which do not necessarily align with the three

orthogonal axes as shown in Fig. 4(a). Images of

buildings can also be taken from a critical viewpoint

where false initial groupings occur (Fig. 4(d)). The

problem of false grouping can also easily occur

when the vanishing points’ initial position is decided

by the intersection of lines with similar orientations.

The refinement method solved this by iteratively

adjusting the position of the vanishing points and

line groupings.

(3) Adaptable to Occlusion, Illumination and

Viewpoint Change. These factors need to be

considered when dealing with building images. Fig.

5 shows some of the rectified building facades using

the proposed method that have been successfully

adapted. At the rectification stage, the accuracy of

each vanishing point obtained with the final grouped

line segments in each vanishing direction set can be

also assessed by investigating parallel lines after

applying the projective transformation P. In theory,

the projective matrix P can recover the lines to

affinity. This means that the line direction in each

group should be the same. From the experiment, the

average deviation error was 1.8%. Fig. 6 shows the

plots of parallel deviation errors for the first three

building example of Fig. 5. In addition, instead of

directly applying computed projective, affine and

similarity transformations to the original image, the

three-stage transformations were only applied to

grouped line sets. After the final transformation,

three least-deviating (from parallel to x or y axis)

line segments were selected for final image

registration in order to reduce rectification distortion

introduced by lines with large deviation errors.

4 CONCLUSIONS

In conclusion, our approach for building facade

rectification is generally robust to occlusions,

different illuminations, wide changes in viewpoint

and different camera settings. The method could be

improved further by analysing the peaks detected at

the stage of curve fitting. For example, instead of

selecting the highest two or three peaks for grouping,

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

minor peaks could also be included. Groups with

similar initial estimates could be combined at the

refinement stage. This kind of improvement can also

enable rectification of a collection of buildings

appeared in a single image.

REFERENCES

Chen, Y & Ip, H, H, S 2005, ‘Planar metric rectification

by algebraically estimating the image of the absolute

conic’, In Proc IEEE conf. on Pattern Recognition, vol.

38, pp. 1117-1120.

David, P 2008, ‘Detection of building facades in urban

environments’, In Proc. SPIE conf. on Visual

Information Processing XV!!, vol. 6978, pp.

9780-9780.

Hartley, R, I 1999. ‘Theory and practice of projective

rectification’, International Journal of Computer

Vision, vol. 35, pp. 115-127.

Hu, J, Sawyer, J & Herve, J, Y 2006, ‘Building detection

and recognition for an automated tour guide’, In Proc.

IEEE Conf. on Systems, Man and Cybernetics, vol. 1,

pp. 283-289.

Košecká, J & Zhang, W 2002, ‘Video compass’, In

Computer Vision — ECCV, vol. 2353, pp. 29-32.

Košecká, J & Zhang, W 2005, ‘Extraction, matching, and

pose recovery based on dominant rectangular

structures’, Computer Vision and Image

Understanding, vol. 100, pp. 274-293.

Liebowitz, D & Zisserman, A 1998, ‘Metric rectification

for perspective images of planes’, In Proc. IEEE Conf.

on Computer Vision and Pattern Recognition, pp.

482-488.

Menudet, J, F, Becker, J, M, Fournel, T & Mennessier, C

2008, ‘Plane-based camera self-calibration by metric

rectification of images’, Image and Vision Computing,

vol. 26, pp. 913-934.

Robertson, D & Cipolla, R 2004. ‘An image-based system

for urban navigation’, In Proc. British Machine Vision

Conference.

Wang, G, Hu, Z, Wu, F & Tsui, H, T 2005, ‘Single view

metrology from scene constraints’, Image and Vision

Computing, vol. 23, pp. 831-840.

Kovesi, P 2000-2006,

http://www.csse.uwa.edu.au/~pk/research/matlabfns/

Shao, T, S, H & Gool, L, V (2003), ‘Zubud-zurich

buildings database for image based recognition’,

Technical report No. 260, Swiss Federal Institute of

Technology,

http://www.vision.ee.ethz.ch/showroom/zubud/

Hartley, R, & Zisserman, A 2003, Multiple View

Geometry in Computer Vision, Cambridge University

Press, Second Edition, Chapter 8.

AUTOMATIC APPROACH FOR RECTIFYING BUILDING FACADES FROM A SINGLE UNCALIBRATED IMAGE