A DECENTRALIZED COLLISION AVOIDANCE ALGORITHM FOR

MULTI-ROBOTS NAVIGATION

Michael Defoort, Arnaud Doniec and Noury Bouraqadi

Ecole de Mines de Douai, 941 rue Charles Bourseul, BP 10838, 59508 Douai, France

Keywords:

Decentralized intelligence, Real-time path planning, Collision avoidance, Receding horizon, Nonholonomic

mobile robots.

Abstract:

This paper presents a distributed strategy for the navigation of multiple autonomous robots. The proposed

planning scheme combines a decentralized receding horizon motion planner, in which each robot computes its

own planned trajectory locally, with a fast navigation controller based on artiﬁcial potential ﬁelds and sliding

mode control technique. This algorithm solves the collision avoidance problem. It explicitly accounts for

computation time and is decentralized, making it suited for real time applications. Simulation studies are

provided in order to show the effectiveness of the proposed approach.

1 INTRODUCTION

The research effort in multi-robots systems (MRS) re-

lies on the fact that multiple robots have the possibil-

ity to perform a mission more efﬁciently than a sin-

gle robot. Among all the topics of study in this ﬁeld,

the issue of conﬂict resolution becomes an increas-

ingly important point. Many cooperative tasks such

as surveillance, search, rescue or area data acquisi-

tion need the robots to autonomously navigate with-

out collision.

Solving conﬂicts in MRS consists in introduc-

ing some coordination mechanisms in order to give

a coherence between the robot acts (Kuchar and

Yang, 2000). For motion planning, three coordination

mechanisms are identiﬁed:

• The Coordination by Adjustment, where each

robot adapts its behavior to achieve a common ob-

jective (Tomlin et al., 1998). However, most of the

planning algorithms are centralized, which often

limit their applicability in real systems.

• The Coordination by Leadership (or supervision)

where a hierarchical relationship exists between

robots (Das et al., 2002). Such an approach is easy

to implement. However, due to the lack of an ex-

plicit feedback from the followers to the leader,

the collision avoidance cannot be guaranteed if

followers are perturbed (during obstacle avoid-

ance for instance). Another disadvantage is that

the leader is a single point of failure.

• The Standardization where procedures are prede-

ﬁned to solve some particular interaction cases

(Pallatino et al., 2007). While this approach can

lead to straightforward proofs, it also tends to be

less ﬂexible with respect to changing conditions.

Here, the problem of interest is the decentralized

navigation for autonomous robots through a coordi-

nation by adjustment. Each vehicle is modeled as

an unicycle with a limited sensing range in order

to capture the essential properties of a wide range

of vehicles. They are dynamically decoupled but

have common constraints that make some conﬂicts.

Indeed, each robot has to avoid collision with the

other entities. Furthermore, the proposed framework

allows moving (and static) obstacles to be avoided

since they can be modeled as non cooperative enti-

ties.

Motion planning consists in generating a

collision-free trajectory from the initial to the ﬁnal

desired positions for a robot. Since the environment

is partially known and further explored in real

time, the computation of complete trajectories from

start until ﬁnish must be avoided. Therefore, the

trajectories have to be computed gradually over time

while the mission unfolds. It can be accomplished

using an online receding horizon planner (Mayne

et al., 2000), in which partial trajectories from an

initial state toward the goal are computed by solving

optimal control problems over a limited horizon.

Two strategies for motion planning in MRS

Michael D., Doniec A. and Bouraqadi N. (2009).

A DECENTRALIZED COLLISION AVOIDANCE ALGORITHM FOR MULTI-ROBOTS NAVIGATION.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 44-51

DOI: 10.5220/0002194900440051

 SciTePress

are the centralized and decentralized (distributed)

approaches. Although the centralized one has been

used in different studies (see (Dunbar and Murray,

2002) for instance), its computation time which

scales exponentially with the number of robots, its

communication requirement and its lack of security

make it prohibitive. To overcome these limitations,

one can use a distributed strategy which results in be-

haviors closed to what is obtained with a centralized

approach. Recently, some decentralized receding

horizon planners have been proposed. In (Dunbar

and Murray, 2006), a distributed solution is provided

for the rigid formation stabilization problem.

In (Kuwata et al., 2006), the navigation problem is

solved through a coordination by leadership. Indeed,

the robots update their trajectory sequentially. In

(Defoort et al., 2007), a decentralized algorithm

based on a coordination by adjustment is proposed

to solve the navigation problem for MRS. However,

the large amount of information exchanged between

robots and the addition of several constraints make

this strategy prohibitive when the number of vehicles

increases.

One of other collision avoidance algorithm is

potential ﬁeld method, where an artiﬁcial potential

function treats each robot as a charged particle

that repels all the other entities (Latombe, 1991;

De-Gennaro and Jadbabaie, 2006). However, most of

them are only based on relative position information

and do not consider coordination between coopera-

tive robots.

In this paper, we proposed a practical decentral-

ized scheme, based on a coordination by adjustment,

for real time navigation of large-scale MRS. As

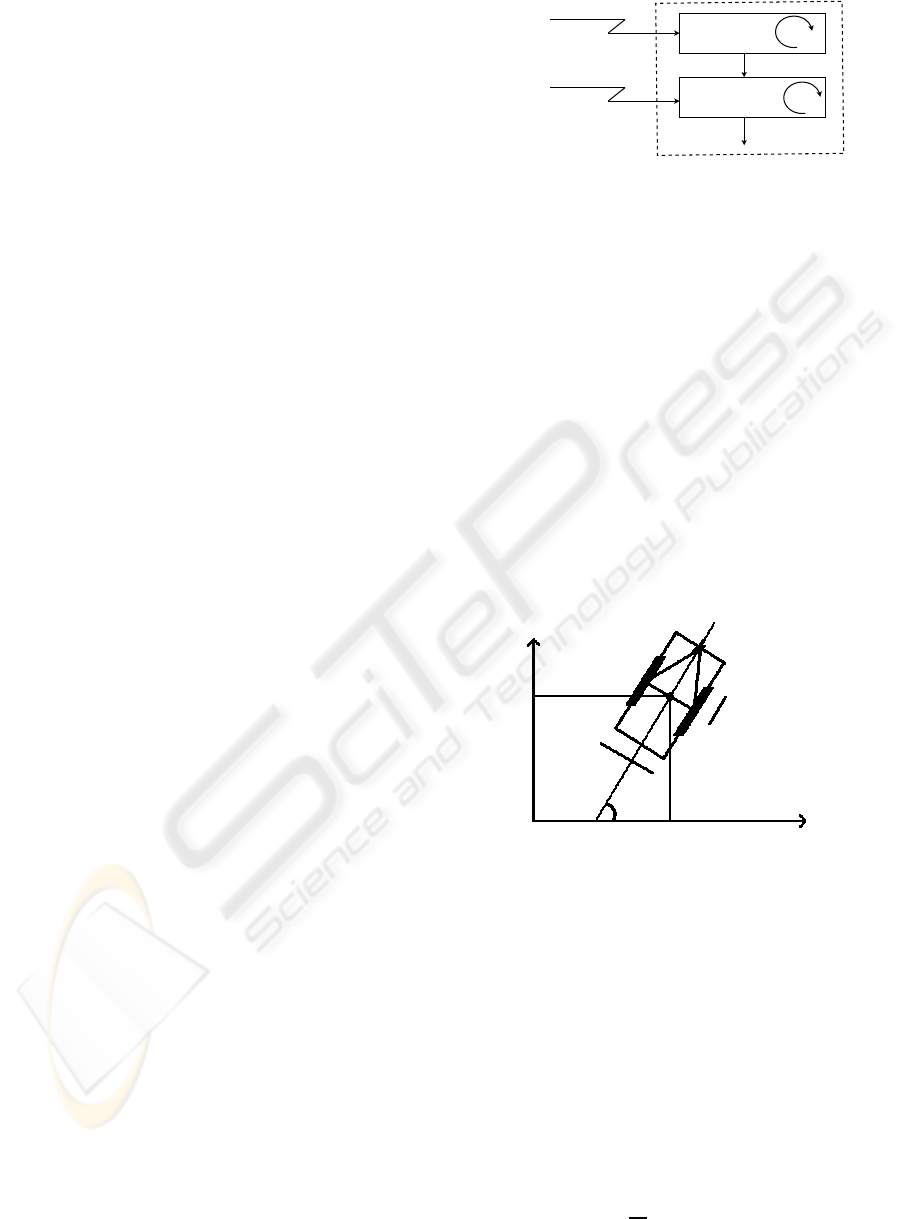
illustrated in Fig. 1, the scheme consists of two

parallel processes:

• a distributed receding horizon planner, in which

each robot computes its own planned trajectory

locally, for the coordination between cooperative

robots,

• a reactive approach, which combines artiﬁcial po-

tential ﬁelds and sliding mode control technique,

for simultaneously tracking the planned trajectory

while avoiding collision with unexpected entities

(i.e. non cooperative entities).

The main advantages of the proposed strategy, espe-

cially for large-scale MRS, are the small amount of in-

formation exchanged between cooperative robots and

the robustness.

The outline of this paper is as follows. In Section

2, the problem setup is described. In Section 3, the

navigation algorithm is presented. Finally, numerical

results illustrate the effectiveness of the strategy.

Robot A

Receding horizon

planner

planned trajectory

real control inputs

Reactive navigation

controller

planned velocity

of cooperative robots

actual position and velocity

Process 1

Process 2

of non cooperative entities

actual position and velocity

(obstacles, moving objects)

Figure 1: Proposed navigation algorithm.

2 PROBLEM STATEMENT

2.1 Dynamic Model of the Robots

Each robot A

(n ∈ (1, ..., N) with N ∈ N), shown

in Fig. 2, is of unicycle-type. Its two ﬁxed driving

wheels of radius r

, separated by 2ρ

, are indepen-

dently controlled by two actuators (DC motors) and

the passive wheel prevents the robot from tipping over

as it moves on a plane. Its conﬁguration is given by:

= [x

,θ

]

where (x

) is the position of its mass center C

and

is its orientation in the global frame.

2ρ





Figure 2: Unicycle-type robot.

The dynamic model of robot A

is given as in (Do

et al., 2004):

= J(η

(1)

+ D

= τ

(2)

where

• M

is a symmetric positive deﬁnite inertia matrix

• D

is a symmetric damping matrix

• the transformation matrix J(η

) is

J(η

) =





cosθ

sinθ

−1

−ρ

−1





(3)

A DECENTRALIZED COLLISION AVOIDANCE ALGORITHM FOR MULTI-ROBOTS NAVIGATION

• z

= [z

]

where z

, z

are the angular veloci-

ties of the right and left wheels. The relationship

between z

and the linear and angular velocities,

denoted v

, w

, is





= B





with B



1 ρ

1 −ρ



(4)

• τ

= [τ

,τ

]

where τ

,τ

are the control torques

applied to the wheels of the robot

Remark 1. System (1)-(2) is ﬂat (see (Fliess et al.,

1995) for details about ﬂatness) since all system vari-

ables can be differentially parameterized by x

, y

well as a ﬁnite number of their time derivatives. For

instance, θ

, v

and w

can be expressed as

= arctan

˙y

˙x

, v

˙x

+ ˙y

, w

¨y

˙x

− ¨x

˙y

˙x

+ ˙y

Remark 2. Speed u

= [ ˙x

, ˙y

]

of A

is restricted to

lie in a closed interval S



∈ R

| ku

k ≤ u

n,max



(5)

2.2 Assumptions and Control Objective

Assumption 1. The following assumptions are made:

• A

knows its position p

= [x

]

and its veloc-

ity u

= [ ˙x

, ˙y

]

• A

has a physical safety area, which is centered

at C

with a radius R

, and has a circular com-

munication area which is also centered at C

with

a radius

. Note that

is strictly larger than

+ R

, j ∈ (1, .. ., N), j 6= n

• A

broadcasts (p

) and receives (p

)

broadcasted by other cooperative robots A

, in its

communication area

• A

can compute the relative position and velocity

obs

) of non cooperative entities within a

given sensing range

• At the initial time t

ini

≥ 0, each robot starts at a

location outside of the safety areas of other enti-

ties

The objective is to ﬁnd the control inputs τ

for

each robot A

such that, under Assumption 1,

• A

is stabilized toward its desired point p

n,des

, i.e.

lim

t→∞

(t) − p

n,des

k = 0 (6)

• collisions are avoided

• all computations are done on board in a decentral-

ized cooperative way

Remark 3. It should be noted that for collision avoid-

ance, one can distinguish two kinds of entities, i.e.

• cooperative robots which are involved in a de-

tected potential collision

• non cooperative entities which cannot cooperate

in the collision avoidance process. They represent

the moving objects and static obstacles.

3 DISTRIBUTED ALGORITHM

In order to solve the multi-robots navigation problem,

a decentralized algorithm combining two parallel pro-

cesses is proposed. First, a receding horizon planner,

in which each robot computes its own planned trajec-

tory locally, achieves middle-term objectives, i.e. co-

ordination between cooperative robots which are in-

volved in a detected potential collision. Then, a reac-

tive navigation controller is proposed to fulﬁll short-

term objectives, i.e. trajectory tracking while taking

into account non cooperative entities.

3.1 Conﬂicts and Collisions

Deﬁnition 1. (conﬂict) A conﬂict occurs between two

cooperative robots A

and A

at time t

∈ R

if they

are not in collision at t

, but at some future time, a

collision may occur.

The following proposition, based on the well-

known concept of velocity obstacle (Fiorini and

Shiller, 1998), is useful to check the presence of con-

ﬂicts.

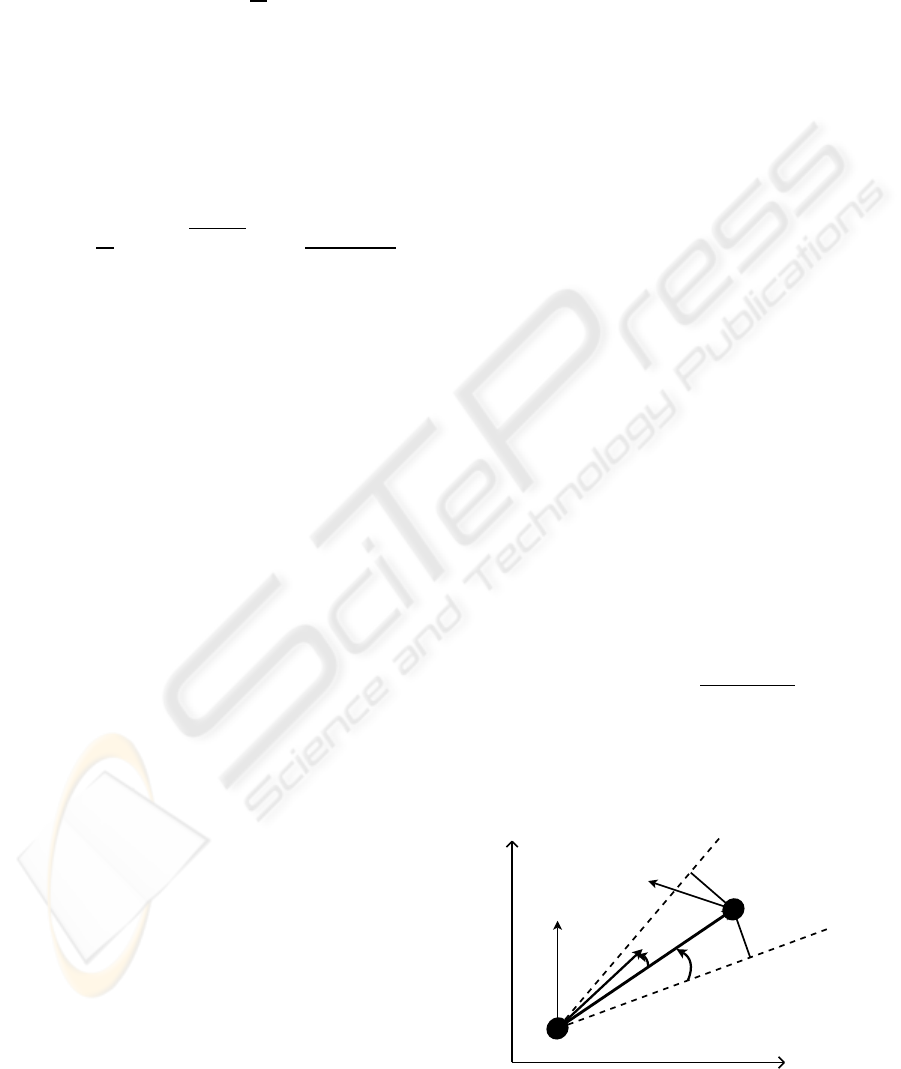
Proposition 1. Let us deﬁne for each pair (A

the following variables depicted in Fig. 3:

) = arg(u

) −u

)) −arg(p

) − p

))

) = arcsin



)−p



(7)

A necessary and sufﬁcient condition for no conﬂict be-

tween A

and A

at t

is:

|β

)| ≥ α

) (8)

+ R

− u

Figure 3: Velocity obstacle concept.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

Deﬁnition 2. (conﬂict subset) For each A

, the con-

ﬂict subset N

) at time t

∈ R

is the set of all co-

operative robots which are in the communication area

of A

and in conﬂict with A

3.2 Receding Horizon Planner

The purpose of the distributed receding horizon plan-

ner is to decompose the overall problem into a family

of simple receding horizon planning problems which

are implemented in each robot A

In every problem, the same planning horizon T

∈

and update period T

∈ R

< T

) are used.

The receding horizon updates are

= t

ini

+ (k − 1)T

, k ∈ N

∗

(9)

Remark 4. During the initialization step, that is to

say before robots move, we denote t

= t

ini

At each update t

, robots in conﬂict exchange in-

formation about each others (position, velocity, .. .).

Then, in parallel, every robot A

computes an antic-

ipated trajectory, denoted

(t,t

) and an anticipated

velocity

(t,t

), over the overall horizon, for all A

belonging to N

). These trajectories are obtained

without taking the collision avoidance constraint into

account. Therefore, by design, the anticipated trajec-

tory is the same in every receding horizon planning

problem in which it occurs. At last, in parallel, ev-

ery robot A

computes only its own planned trajec-

tory p

∗

(t,t

) and planned velocity u

∗

(t,t

), over the

planning horizon T

, in order to integrate the colli-

sion avoidance between cooperative robots. From the

planned trajectory and velocity associated to the plan-

ning horizon T

, only the part which corresponds to

the update horizon T

is stored.

Remark 5. Note that the ﬁrst argument of p

∗

and

denotes time. The second argument is only

added to distinguish at which receding horizon update

the trajectory and velocity are computed.

The collection of distributed receding horizon

planning problems is formally deﬁned as Problems 1-

2 for each robot A

Problem 1. For each robot A

and at any update t

k ∈ N:

Given

: the actual positions p

), p

) and the ac-

tual velocities u

), u

) of robot A

and robots A

belonging to N

), respectively.

Find

: the anticipated trajectory and velocity pairs

(

(t,t

)), ∀i ∈



i ∈ N | A

∈ N

) ∪ {A

}



subject to the following constraints:







) = p

)

) = u

)

(t,t

) ∈ S

, ∀t ≥ t

(10)

The anticipated trajectories are computed without

taking the collision avoidance constraint into account.

That is why, to integrate the path planning with local

collision avoidance, the following problem is solved.

Problem 2. For each robot A

and at any update t

k ∈ N:

Given

: the anticipated pairs (

(t,t

)), ∀i ∈



i ∈ N | A

∈ N

) ∪ {A

}



Find

: the planned trajectory and velocity pairs

∗

(t,t

),u

∗

(t,t

)) that minimizes

k+1

∑

nj,rep

(t) + kp

∗

(t,t

) −

(t,t

(11)

subject to the following constraints:







∗

k+1

) = p

∗

k+1

k−1

)

∗

k+1

) = u

∗

k+1

k−1

)

∗

(t,t

) ∈ S

, ∀t ∈



k+1

+ T



(12)

where

nj,rep

(t) =

(

0 if

(t) ≥ b



(t)

−



else

(t) = kp

∗

(t,t

) −

(t,t

)k −(R

+ R

)

(13)

and b

are strictly positive factors which can vary

among robots to reﬂect differences in aggressiveness

< 1, b

≪ 1) and shyness (a

> 1, b

≫ 1).

One can note that the ﬁrst part of cost (11) is de-

signed to enforce the collision avoidance between co-

operative robots. The cost term kp

∗

(t,t

) −

(t,t

in (11) is a way of penalizing the deviation of the

planned trajectory p

∗

(t,t

) from the anticipated tra-

jectory

(t,t

), which is the trajectory that other

robots rely on. In previous work, this term was incor-

porated into the decentralized receding horizon plan-

ner as a constraint (Defoort et al., 2007). The formu-

lation presented here is an improvement over this past

formulation, since the penalty yields an optimization

problem that is much easier to solve.

Remark 6. One can note that constraints (12) which

guarantee the continuity of the planned trajectory and

velocity need p

∗

k+1

k−1

) and u

∗

k+1

k−1

) com-

puted in the previous step. Therefore, the proposed

planner is not able to reject external disturbances or

inherent discrepancies between the model and the real

process. However, it takes the real time constraint

into account. Indeed, each robot has a limited time

to plan its trajectory. The time allocated to make its

decision depends on its perception sensors, its com-

putation delays and is less than the update period T

(see Fig. 4).

The discussed claim for robustness in trajectory track-

ing will be achieved hereafter.

A DECENTRALIZED COLLISION AVOIDANCE ALGORITHM FOR MULTI-ROBOTS NAVIGATION

k+1

Anticipated trajectory

Planned trajectory

∗

(t, t

k−1

)

∗

(t, t

)

∗

(t, t

)

Comput.

∗

(t, t

k+1

)

Figure 4: Implementation of the receding horizon planner.

Remark 7. A compromise must be done between re-

activity and computation time. Indeed, the planning

horizon must be sufﬁciently small in order to have

good enough results in terms of computation time.

However, it must be higher than the update period to

guarantee enough reactivity.

Remark 8. To numerically solve Problems 1-2, a

nonlinear trajectory generation algorithm (Defoort

et al., 2009) is applied. It is based on ﬁnding tra-

jectory curves in a lower dimensional space and pa-

rameterizing these curves by B-splines. A constrained

feasible sequential quadratic optimization algorithm

is used to ﬁnd the B-splines coefﬁcients that optimize

the performance objective while respecting the con-

straints.

3.3 Reactive Navigation Controller

Hereafter, a reactive approach, which combines arti-

ﬁcial potential ﬁelds and sliding mode control tech-

nique, for simultaneously tracking the planned trajec-

tory while avoiding collision with unexpected entities

(i.e. non cooperative entities), is proposed.

Since the robot dynamics (1)-(2) is of strict feed-

back systems (see (Krstic et al., 1995) for details

about strict feedback systems) with respect to the

robot linear and angular velocities (i.e. v

and w

), a

backstepping procedure is used to design the control

input τ

. That is why the control design is divided

into two main steps.

3.3.1 Step 1 based on Artiﬁcial Potential Fields

Let us introduce the following notations:



= θ

− γ

= v

− γ

(14)

where γ

and γ

are auxiliary variables used to avoid

collisions. Replacing expressions (14) into the ﬁrst

two equations of (1) and using (4) yield:



cosγ

sinγ



+ ∆

(15)

with ∆

= γ



(cosθ

− 1)cosγ

− sinθ

sinγ

sinθ

cosγ

+ (cosθ

− 1)sinγ



and ∆

= v



cosθ

sinθ



The objective is to design the auxiliary variables

and γ

such that robot A

robustly tracks its

planned trajectory p

∗

while avoiding unexpected col-

lisions. Here, artiﬁcial potential functions are used in

order to design an attractive force between the robot

and its planned trajectory and a repulsive force to

avoid collisions.

In conventional potential ﬁeld method (Latombe,

1991), the planned robot velocity u

∗

is assumed to

be zero and the obstacle velocity u

obs

is not consid-

ered. However, to make robot A

track the planned

trajectory among moving obstacles, velocities u

∗

and

obs

play key roles. This issue will be addressed

by extending the results given in (Huang, 2009).

Let us consider the conventional potential function

(Latombe, 1991):

= U

n,att

n,rep

(16)

where U

n,att

and U

n,rep

are, respectively, the attractive

potential deﬁned to track the planned trajectory p

∗

and the repulsive potential related to collision avoid-

ance, speciﬁed as follows:

• The attractive potential is designed such that it

puts penalty on the tracking error and is equal to

zero when the robot is at its desired position, i.e.

n,att

− p

∗

(17)

• The repulsive potential is designed such that it

equals to inﬁnity when a collision occurs with A

and decreases according to the relative distance

between A

and an obstacle, i.e.

n,rep

= c

∑

ni,rep

(18)

with

ni,rep

(

0 if ρ

≥ d



−



else

(19)

where

is the minimum distance between robot A

and

the obstacle i. c

and d

are strictly positive fac-

tors which have similar properties as a

and b

Proposition 2. If the errors θ

and v

are asymptot-

ically stable, A

robustly tracks its planned trajectory

∗

while avoiding collisions using the auxiliary vari-

ables:

[(ku

∗

kcos(θ

∗

− ψ

) − c

∑

obs

kcos(θ

obs

− ψ

)

+kp

− p

∗

+ ku

∗

sin

(θ

∗

−

)]

0.5

+ arcsin



∗

k sin(θ

∗

−

)



(20)

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

with

∗

= arg(u

∗

)

obs

= arg(u

obs

)

= arg(p

∗

− p

)

= arg(p

obs

− p

)

= arctan



sinψ

−c

∑

sinψ

cosψ

−c

∑

cosψ



(

0 if ρ

≥ d



−



(ρ

)

−p

∗

else

Proof. Let us differentiate U

with respect to time in

equation (16), i.e.:

n,att

n,rep

(21)

Substituting (20) into (21) yields after some geomet-

ric manipulations:

= kp

∗

− p

k(ku

∗

kcos(θ

∗

− ψ

) − γ

cos(γ

− ψ

)

−c

∑



obs

kcos(θ

obs

− ψ

) + γ

cos(γ

− ψ

)



)



− p

∗

)

− c

∑

−p

∗

−p

obs

− p

obs

)



(∆

+ ∆

)

= kp

∗

− p

k(ku

∗

kcos(θ

∗

− ψ

) − γ

cos(γ

−

)

−c

∑



obs

kcos(θ

obs

− ψ

)



)



− p

∗

)

− c

∑

−p

∗

−p

obs

− p

obs

)



(∆

+ ∆

)

= kp

∗

− p

k(ku

∗

kcos(θ

∗

− ψ

) −

− ku

∗

sin

(θ

∗

−

)

−c

∑



obs

kcos(θ

obs

− ψ

)



)



− p

∗

)

− c

∑

−p

∗

−p

obs

− p

obs

)



(∆

+ ∆

)

Assuming that the errors θ

and v

are asymptoti-

cally stable (i.e. ∆

= ∆

= 0), one can get from

(20):

≤ −kp

∗

− p

(22)

Since U

≥ 0 and

≤ 0, U

is bounded. That is

why A

robustly tracks its planned trajectory p

∗

while

avoiding collisions.

3.3.2 Step 2 based on Sliding Mode Technique

Now, the objective is to force the motion of robot A

such that the errors θ

and v

are asymptotically sta-

ble. The proposed strategy is based on the so-called

second order sliding mode control (SMC) approach.

The SMC methodology (Utkin et al., 1999) is cho-

sen because it is a robust technique to control non-

linear systems operating under uncertainty conditions

(Fridman and Levant, 2002). Furthermore, second or-

der SMC can reduce the chattering phenomenon (high

frequency vibrations of the controlled system which

degrade the performances). Indeed, instead of inﬂu-

encing the ﬁrst sliding variable time derivative, the

signum function acts on its second time derivative.

This method can also achieve a better convergence

accuracy with respect to discrete sampling time than

conventional SMC (see (Fridman and Levant, 2002)

for a survey).

Let us apply to system (1)-(2) the following pre-

liminary feedback:

= (M

)

−1

(τ

− D

) (23)

where

= [

]

is the auxiliary control input.

Thus, system (1)-(2) can be expressed as follows:

= J(η





(24)



˙v

˙w



(25)

Since the relative degree of system (24)-(25) with

respect to the sliding variable v

is only one, a dy-

namic extension is done before designing the control

(see (Isidori, 1989) for further details). Thus, an inte-

grator chain is added on the input variable

There are several algorithms to ensure the ﬁnite

time stabilization of the sliding variables θ

and v

towards the origin. Among them, the sampled twist-

ing algorithm (Fridman and Levant, 2002) has been

developed for systems with relative degree two. This

algorithm provides good convergence accuracy and

robustness properties. It does not require the knowl-

edge of the time derivative of the sliding variables and

takes into account some practical constraints such as

the sampling of the measurement and the control.

Proposition 3. Consider system (1)-(2). The errors

and v

are stable in ﬁnite time under the nonlin-

ear controller deﬁned in (23) where



−λ

1,M

sign(θ

) if θ

∆

> 0

−λ

1,m

sign(θ

) if θ

∆

≤ 0



−λ

2,M

sign(v

) if v

∆

> 0

−λ

2,m

sign(v

) if v

∆

≤ 0

(26)

with

∆



0 if k = 0

(kT

) − θ

((k− 1)T

) else

∆



0 if k = 0

(kT

) − v

((k− 1)T

) else

(27)

is the sampling period, k ∈ N is related to the time

of the process and λ

i,m

, λ

i,M

, i = 1,2 are positive con-

stants high enough to enforce the sliding motion.

Proof. It can be shown that this controller ensures

a ﬁnite time convergence of the trajectories onto

the manifold {v

= ˙v

= 0} and



= 0



(see (Fridman and Levant, 2002) for further details).

Hence, the application of the control input (26) re-

sults in the robust ﬁnite time stabilization of θ

and

Remark 9. We would like to emphasize that although

not explicitly considered here the procedure based

on sliding mode control guarantees proper behavior

even in the presence of uncertainties in the mass and

inertia of the robots and additive disturbances to the

linear and angular velocities which constitute very re-

alistic assumptions.

A DECENTRALIZED COLLISION AVOIDANCE ALGORITHM FOR MULTI-ROBOTS NAVIGATION

Once the sliding mode occurs on all the surfaces

(which happens in ﬁnite time), based on Proposition

2, the global control objectives, deﬁned in Section

2.2, are fulﬁlled.

Some speciﬁc advantages of the proposed decentral-

ized algorithm are enumerated below:

• robustness with respect to uncertainties and dis-

turbances (sliding mode controller),

• reactivity (potential ﬁeld functions),

• low communication bandwidth, i.e. small amount

of information is locally exchanged,

• reduction of deadlocks due to local minima in po-

tential ﬁeld (anticipation and coordination mech-

anism through the receding horizon planner).

4 SIMULATION RESULTS

This section demonstrates the performance of the pro-

posed decentralized algorithm. The following simula-

tions showcase two different scenarios for which the

environment is partially known (i.e. the range of sen-

sors of each robot is of radius 1.5m).

The main parameters of the robots are: ∀n, R

0.25m,

= 4m and u

n,max

= 1m/s. For the decen-

tralized algorithm, the following parameters are used:

= 3s, T

= 0.5s, a

= c

= 1, b

= 2, d

= 0.5,

1,M

= λ

2,M

= 10, λ

1,m

= λ

2,m

= 1 and T

= 0.01s.

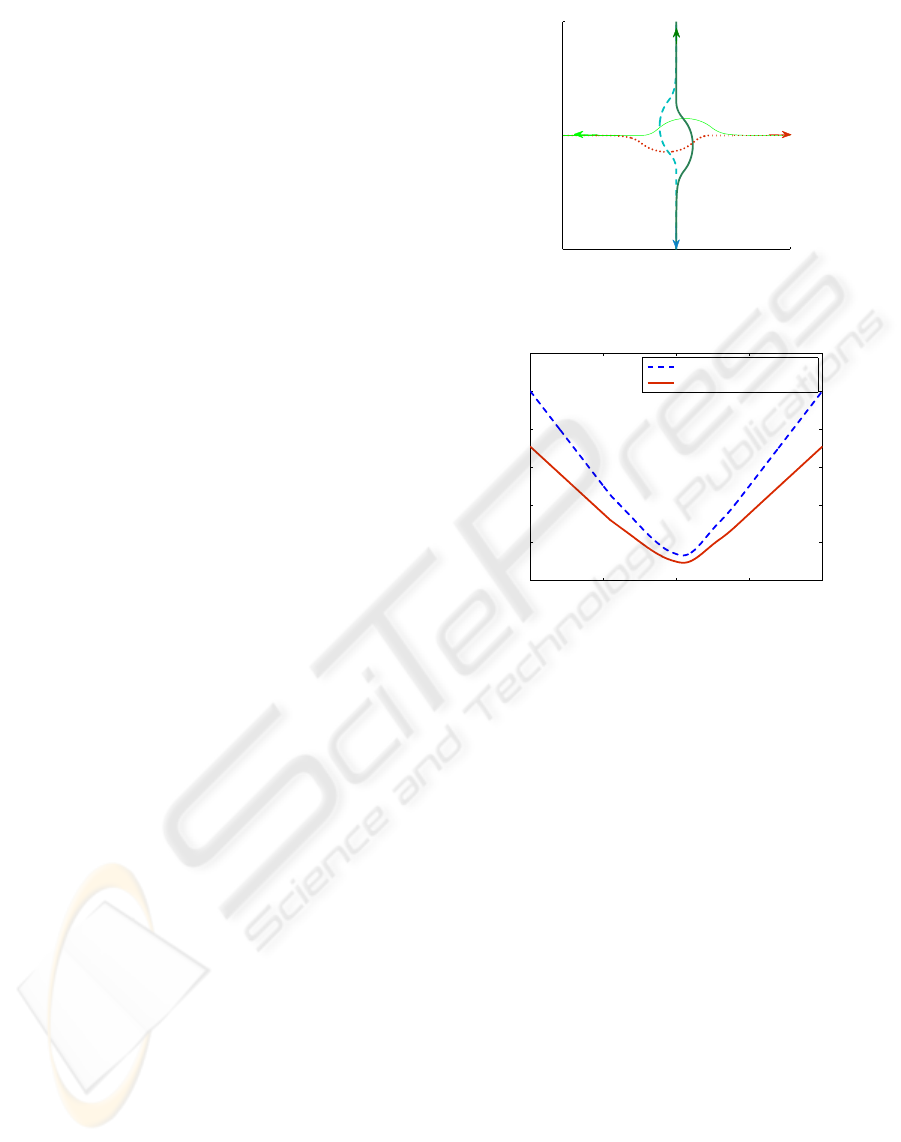
4.1 Scenario 1: Crossing

In this scenario, there are four robots (N = 4) start-

ing at p

ini

) = [5,0]

, p

ini

) = [15, 0]

, p

ini

) =

[10,5]

and p

ini

) = [10,− 5]

respectively, with ve-

locities equal to zero. These robots must cross each

other in order to reach their desired conﬁguration

1,des

= [15,0]

, p

2,des

= [5,0]

, p

3,des

= [10,−5]

and p

4,des

= [10,5]

. One can note that this problem

is not trivial due to its symmetry properties.

The simulation results are given in Fig. 5. One

can see that each robot modiﬁes its trajectory in order

to avoid collision. Figure 5(b) depicts the evolution

of the distance between robots. Since it is higher than

0.5m, the collision avoidance is guaranteed.

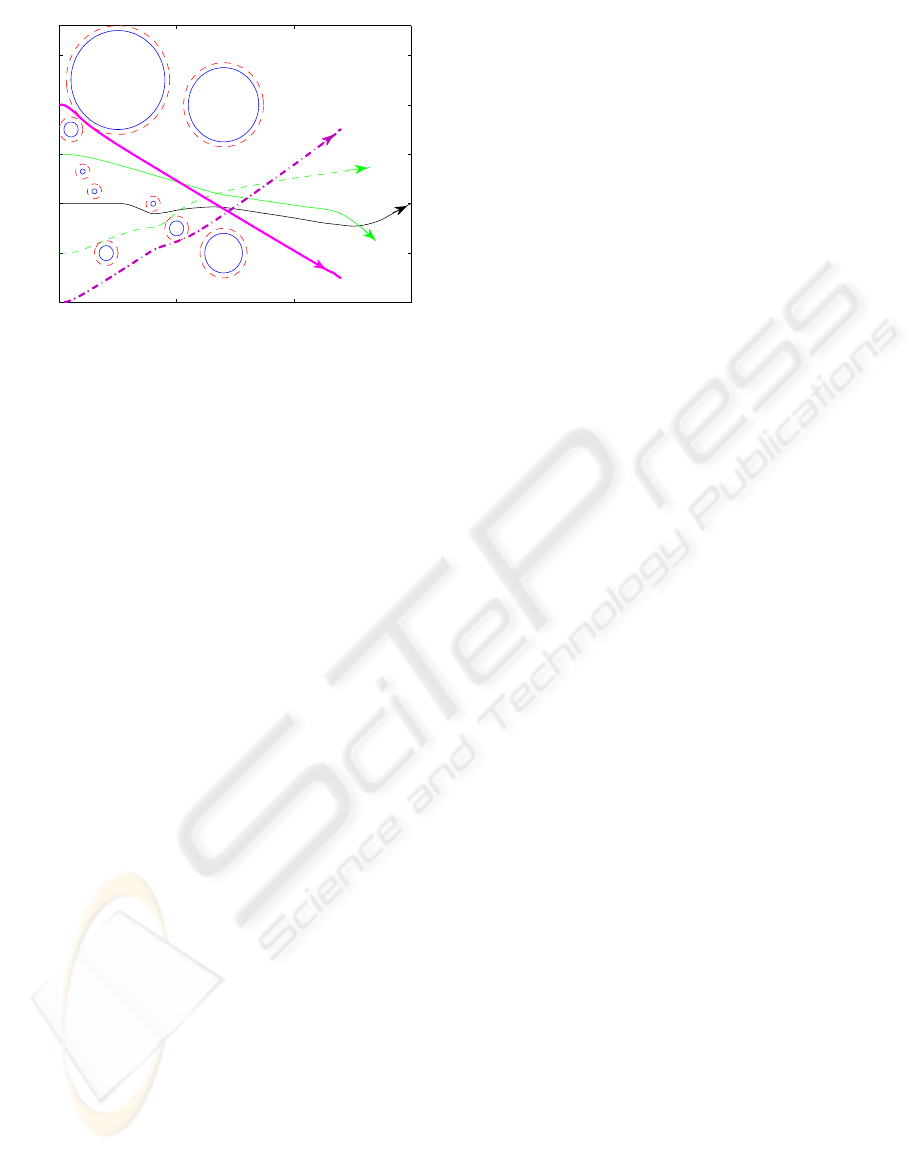
4.2 Scenario 2: Reconﬁguration with

Collision Avoidance

In this scenario, a swarm of ﬁve robots (N = 5) recon-

ﬁgures its geometric shape (from “linear” to “triangu-

lar”) while avoiding collisions with obstacles. The

5 10 15

−5

x(m)

y(m)

(a)

0 5 10 15 20

t(s)

(m)

p

− p



p

− p

 = p

− p



(b)

Figure 5: Four vehicles simulation: (a) Robot trajectories.

(b) Relative distances between A

and other robots.

proposed decentralized controller has only a limited

knowledge of the obstacles (initially unknown). It

simply keeps the robots spaced out using the proposed

potential ﬁeld technique. The ﬁve robots make deci-

sions in order to avoid collisions. One can note that

the number of potential conﬂicts is high.

One can see in Fig. 6 that under the proposed de-

centralized algorithm, the robots meet the objective

deﬁned in Section 2.2. Note that the radius of obsta-

cles is increased by 0.25m (dotted lines around obsta-

cles) to take the size of robots into account.

5 CONCLUSIONS

A new distributed strategy for the navigation of mul-

tiple autonomous robots is presented. The pro-

posed scheme combines a decentralized receding

horizon motion planner to satisfy middle-term objec-

tives (coordination between cooperative robots) with

a fast navigation controller based on artiﬁcial poten-

tial ﬁelds and sliding mode control technique to sat-

isfy short-term objectives (collision avoidance and

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

0 5 10

−4

−2

x (m)

y (m)

obstacle

Figure 6: Collision avoidance of ﬁve robots.

trajectory tracking). The fact that there is no leader

increases the security and the robustness of the mis-

sions. Simulation studies are provided in order to

show the effectiveness of the proposed approach.

Experimental testing on WiﬁBot is under way. In

the future, it is planned to design real time observers

to estimate the relative velocities between robots.

REFERENCES

Das, A., Fierro, R., Kumar, V., Ostrowski, J., Spetzer, J.,

and Taylor, C. (2002). A vision-based formation con-

trol framework. IEEE T. Robotic Autom., 18(5):pp.

813–825.

De-Gennaro, M. and Jadbabaie, A. (2006). Formation con-

trol for a cooperative multi-agent system using decen-

tralized navigation functions. In American Control

Conf.

Defoort, M., Floquet, T., Kokosy, A., and Perruquetti, W.

(2007). Decentralized robust control for multi-vehicle

navigation. In European Control Conf.

Defoort, M., Palos, J., Kokosy, A., Floquet, T., and Perru-

quetti, W. (2009). Performance based reactive nav-

igation for nonholonomic mobile robots. Robotica,

27(2):pp. 281–290.

Do, K., Jiang, Z., and Pan, J. (2004). A global output-

feedback controller for simultaneous tracking and sta-

bilization of unicycle-type mobile robots. IEEE T. Au-

tomat. Contr., 20(3):pp. 589–594.

Dunbar, W. and Murray, R. (2002). Model predictive con-

trol of coordinated multi-vehicle formation. In IEEE

Conf. on Decision and Control.

Dunbar, W. and Murray, R. M. (2006). Distributed receding

horizon control for multi-vehicle formation stabiliza-

tion. Automatica, 42(4):pp. 549–558.

Fiorini, P. and Shiller, Z. (1998). Motion planning in dy-

namic environments using velocity obstacles. Int. J.

Robot. Res., 17(7):pp. 760–772.

Fliess, M., Levine, J., Martin, P., and Rouchon, P. (1995).

Flatness and defect of nonlinear systems: introductory

theory and examples. Int. J. Control, 61(6):pp. 1327–

1361.

Fridman, L. and Levant, A. (2002). Higher order sliding

mode modes. Sliding mode control in Engineering,

Ed W. Perruquetti, J. P. Barbot, pages 53–101.

Huang, L. (2009). Velocity planning for a mobile robot

to track a moving target - a potential ﬁeld approach.

Robot. Auton. Syst., 57(1):pp. 55–63.

Isidori, A. (1989). Nonlinear control systems. Springer,

New York, 2nd edition.

Krstic, M., Kanellakopoulos, I., and Kokotovic, P. (1995).

Nonlinear and adaptative control design. Wiley, N. Y.

Kuchar, J. and Yang, L. (2000). A review of conﬂict detec-

tion and resolution modeling methods. IEEE T. Intell.

Transp., 1(4):pp. 179–189.

Kuwata, Y., Richards, A., Schouwenaraars, T., and How, J.

(2006). Decentralized robust receding horizon con-

trol. In American Control Conf.

Latombe, J. (1991). Robot Motion Planning. Kluwer Aca-

demic Publishers, Norwell, MA.

Mayne, D., Rawlings, J., Rao, C., and Scokaert, P. (2000).

Constrained model predicitive control: Stability and

optimality. Automatica, 36(6):pp. 789–814.

Pallatino, L., Scordio, V., Bicchi, A., and Frazoli, E.

(2007). Decentralized cooperative policy for conﬂict

resolution in multivehicle systems. IEEE T. Robot.,

23(6):pp. 1170–1183.

Tomlin, C., Pappas, G., and Sastry, S. (1998). Conﬂict res-

olution for air trafﬁc management: a study in mul-

tiagent hybrid systems. IEEE T. Automat. Contr.,

43(4):pp. 509–521.

Utkin, V., Guldner, J., and Shi, J. (1999). Sliding Modes

Control in Electromechanical Systems. Taylor and

Francis, New York.

A DECENTRALIZED COLLISION AVOIDANCE ALGORITHM FOR MULTI-ROBOTS NAVIGATION