
INTERFERENCE REDUCTION THROUGH TASK PARTITIONING
IN A ROBOTIC SWARM
Or: “Don’t you Step on My Blue Suede Shoes!”
Giovanni Pini, Arne Brutschy, Mauro Birattari and Marco Dorigo
IRIDIA, CoDE, Universit
´
e Libre de Bruxelles, Brussels, Belgium
Keywords:
Swarm robotics, Foraging, Self-organized task allocation, Task partitioning, Swarm intelligence.
Abstract:
This article studies the use of task partitioning as a way to reduce interference in a spatially constrained
harvesting task. Interference is one of the key problems in large cooperating groups. We present a simple
method to allocate individuals of a robotic swarm to a partitioned task, and show that task partitioning can
increase system performance by reducing sources of interference. The method is experimentally studied, both
in an environment with a narrow area and an environment without this constraint. The results are analyzed
and compared to the case in which task partitioning is not employed.
1 INTRODUCTION
In collective robotics, interference is a critical prob-
lem limiting the growth of a group: the time each
robot spends in non-task-relevant behaviors such as
obstacle avoidance increases when the density of indi-
viduals rises—see e.g., (Lerman and Galstyan, 2002).
The performance on tasks that suffer from physical
interference can typically be improved by spatial par-
titioning; for example, by keeping each robot in its
own “working area”. A known approach that uses this
rationale is the so called bucket-brigade (Font
´
an and
Matari
´
c, 1996; Shell and Matari
´
c, 2006). In this ap-
proach, robots hand over objects to robots working in
the following area, until the objects reach their des-
tination. As tasks usually cannot be partitioned ar-
bitrarily, this approach effectively limits the number
of robots that can be employed in the task. A pos-
sible solution to this problem, treating working areas
as non-exclusive, raises other problems: How should
individuals be allocated to tasks? How can such an al-
location help in limiting the amount of interference?
In this paper, we study how task partitioning can
help in reducing sources of interference. Additionally,
we show a simple way to achieve self-organized allo-
cation to such a task partition when using a robotic
swarm.
We use the foraging problem, one of the canon-
ical testbeds for collective robotics, as a base for
our studies. In our experiments, a swarm of homo-
geneous robots has to harvest prey objects from a
source area and transport them to a home area. In
this study, we limit ourselves to a harvesting task that
is pre-partitioned by the designer into two subtasks
with a sequential interdependency. We study a sim-
ple threshold-based model of self-organized alloca-
tion and focus on two questions: Under which en-
vironmental conditions is it advantageous to partition
the task? Can this partition reduce interference be-
tween group members? These questions are studied
in two experiments using a simulated robot swarm.
The paper is organized as follows. We first review
related works in Section 2. In Section 3 we explain the
task partitioning and the allocation method employed
in this study. Section 4 gives the methods used in the
experiments by describing the environments, the sim-
ulated robots, and the controller. In Section 5 the re-
sults of the experiments are given and discussed. Sec-
tion 6 draws some conclusions and discusses future
work.
2 RELATED WORK
Interference has long been acknowledged as being
one of the key issues in multi-robot cooperation
(Goldberg and Matari
´
c, 2003). (Lerman and Gal-
styan, 2002) devised a mathematical model that al-
lows a quantification of the interference and its effect
on group performance. Probably, the most thorough
study was published by (Goldberg, 2001), who iden-
tified several types of multi-robot interactions. Gold-
52
Pini G., Brutschy A., Birattari M. and Dorigo M. (2009).
INTERFERENCE REDUCTION THROUGH TASK PARTITIONING IN A ROBOTIC SWARM - Or: "Don’t you Step on My Blue Suede Shoes!".
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 52-59
DOI: 10.5220/0002195200520059
Copyright
c
SciTePress

berg notes that one of the most common types of in-
terference is physical interference in a central area,
for example the nest. This kind of interference results
from resource conflicts, in this case physical space,
and can be arbitrated by either making sure that robots
stay in different areas all the time or by employing a
scheduling mechanism to ensure that robots use the
same space only at different times.
A simple method for reducing interference by us-
ing the first arbitration method mentioned is the so-
called bucket-brigade: robots are forced to stay in
exclusive working areas and to pass objects to the
following robot as soon as they cross the bound-
aries of their area (Font
´
an and Matari
´
c, 1996; Shell
and Matari
´
c, 2006). Recently, this has been ex-
tended to work with adaptive working areas by (Lein
and Vaughan, 2008). To the best of our knowledge,
current works concerned with bucket brigading only
studied the influence of interference due to obstacle
avoidance. Other sources of interference (e.g., ob-
ject manipulation) were never studied, although they
might have a critical impact on the performance of
any task partitioning approach. To quote (Shell and
Matari
´
c, 2006): “If the cost of picking up or dropping
pucks is significant [. . . ], then bucket brigading may
not be suitable.”
Task allocation for multi-robot systems is a wide
field, which can be divided in intentional and self-
organized task allocation. Intentional task allocation
relies on negotiation and explicit communication to
create global allocations, whereas in self-organized
task allocation global allocations result from local,
stochastic decisions. A formal analysis and taxon-
omy that covers intentional task allocation has been
proposed by (Gerkey and Matari
´
c, 2004). (Kalra
and Martinoli, 2006) recently compared the two best-
known approaches of intentional and self-organized
task allocation.
The field of self-organized task allocation is in
its early stages, as most studies tackle simple prob-
lems without task interdependencies. Studies in
self-organized task allocation are mostly based on
threshold-based approaches, taking inspiration from
division of labor in social insects. (Krieger and Bil-
leter, 2000) were among the first to propose threshold-
based approaches in multi-robot task allocation. (La-
bella et al., 2006) used threshold-based task alloca-
tion in a multi-foraging task. Similarly, (Campo and
Dorigo, 2007) used a notion of the group’s internal
energy to allocate individuals to a multi-foraging task.
Finally, (Liu et al., 2007) studied a multi-foraging task
while focusing on the influence of the use of different
social cues on the overall group performance.
3 TASK PARTITIONING
AND ALLOCATION
In this work, we study a collective foraging task. By
spatially partitioning the environment, the global for-
aging task is automatically partitioned into two sub-
tasks: 1) harvesting prey objects from a harvesting
area (source) and 2) transporting them to a home area
(nest). Robots working on the first subtask harvest
prey objects from the source and pass them to the
robots working on the second subtask, which store the
objects in the nest. These subtasks have a sequential
interdependency in the sense that they have to be per-
formed one after the other in order to complete the
global task once: delivering a prey object to the home
area.
Robots can decide to switch from one subtask to
the other, thus creating a task allocation problem: in-
dividual robots have to be allocated to subtasks and
different allocations yield different performance. As
a prey object has to be passed directly from one robot
to the other, a robot usually has to wait some time be-
fore passing a prey object to or receiving a prey object
from a robot working on the other subtask. This wait-
ing time can therefore give an indication of the alloca-
tion quality for the respective subtask: if the waiting
time is very long, there might not be enough robots al-
located to the other subtask. Thus, the robots can use
this waiting time to decide whether to switch subtask
or not. Ideally, the waiting time should be the same
for the two subtasks in order for the system to reach a
stable state and deliver optimal performance.
Our robots exploit a simple threshold-based model
to decide when to switch task: when the waiting time
t
w
is higher than a threshold Θ, a robot switches its
subtask. The robot’s waiting time is a function of the
average time the robots working in the other subtask
need to complete their task. The task-completion time
of a robot depends on two factors: 1) round-trip-time
(i.e., distance to travel) and 2) time lost due to interfer-
ence. Thus, the robot’s threshold Θ is a function of the
round-trip-time and the interference of the robots in
the other subtask. Therefore, the optimal task switch-
ing threshold depends on the task (i.e., time to harvest
a prey object) and the environment (i.e., distance be-
tween the source and the nest). As the parameters
of the environment are not pre-programmed into the
robots, determining the optimal threshold can be a
complex problem. In this work, we limit ourselves
to a simple method for setting this threshold: at the
start of the experiment, each robot draws a random
threshold that is used as its task switching threshold
throughout the experiment.
In the following, we study the properties of this
INTERFERENCE REDUCTION THROUGH TASK PARTITIONING IN A ROBOTIC SWARM - Or: "Don't you Step
on My Blue Suede Shoes!"
53

simple self-organized task allocation strategy, com-
pare this strategy to a strategy without task partition-
ing, and analyze how it can help to reduce interfer-
ence. We refer to the two strategies as partitioned and
non-partitioned, respectively.
4 METHODS
This section describes the environments in which the
experiments are carried out, the simulated robots, and
the robot’s controller. Additionally, we describe how
we run the experiments and we introduce some met-
rics that we use to evaluate the properties of the sys-
tem.
4.1 Environments
We study task allocation in two different environ-
ments. In these two environments, the nest is marked
by a light source that can be perceived by all robots,
thus providing directional information. The environ-
ment is spatially partitioned in two parts: the source
is located on the left and the nest is located on the
right side of the arena. We refer to the two sides
of the arena as harvest area and store area, respec-
tively. The exchange zone is located between these
two areas. Robots working on the left side, called
harvesters, gather prey objects in the source and move
them to the exchange zone, where they pass them to
the robots working on the other side. These are re-
ferred to as storers: their role is to transport prey
objects to the nest and store them there. The nest,
the source, and the exchange zone can be detected
through environmental cues (ground color).
At time t = 0, the robots are randomly placed
in the harvest area. The experiments run for t
max
=
18,000 time steps (a simulated time of one hour, with
a time step length of 200 ms). The experiments are run
in two different arenas (see Figure 1). The first arena
(Figure 1a) is 4.125m long with a width of 1.6m at
the source and exchange zone, whereas the nest is
0.4m wide. The exchange zone is located 3.125m
away from the source. This arena is characterized by
the presence of an area, critical for the task, in which
high interference between robots can be expected (the
nest). Thus, this arena is referred to as the narrow-
nest environment.
The second arena (Figure 1b) has a rectangular
shape: it is 3.75 m long and 1.6 m wide. Here as well
the exchange zone is located 3.125m from the source.
The arena shape does not suggest the presence of any
zone where interference can be higher than in other
Figure 1: Depiction of (a) the narrow-nest environment
used in the first experiment and (b) the wide-nest environ-
ment used in the second experiment. The gray stripes are
the source (left), and the nest (right), each 0.25 m deep. The
black stripe is the exchange zone, that is 0.5 m deep. The
light source is marked with “L”.
places. This arena is referred to as the wide-nest en-
vironment.
The area of both arenas is 6 m
2
, 5 m
2
for the har-
vest area and 1m
2
for the store area. The overall area
is the same in the two arenas, so that the same group
size results in the same robot density. Thus, results
are comparable across the two environments.
4.2 Simulation
The experiments are carried out in a custom simula-
tion environment that models geometries and func-
tional properties of simple objects and robots. Our
robots’ model is purely kinematic. Prey objects are
simulated as an attribute a robot can posses and not as
physical entities. Although the experiments are con-
ducted in simulation only, the simulated robots have
a real counterpart: the swarm-bot robotic platform
(Mondada et al., 2004). The platform consists of a
number of mobile autonomous robots called s-bots,
which have been used for several studies, mainly in
swarm intelligence and collective robotics—see for
instance (Groß et al., 2006) and (Nouyan et al., 2008).
The simulated s-bots are of round shape, with a diam-
eter of 0.116 m. Each of them is equipped with 16
infrared proximity sensors, used to perceive obstacles
up to a distance of 0.15 m. Eight ambient light sensors
can be used to perceive light gradients up to a distance
of 5.0 m. The robots are equipped with 4 ground sen-
sors used to perceive nest, source and exchange zone.
A 8 LEDs ring is used to signal when a prey object
is carried. An omnidirectional camera allows the per-
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
54
ception of LEDs in a circle of radius 0.6m surround-
ing the robot. A uniform noise of 10% is added to all
sensor readings at each simulation step. The robots
can move at a maximum speed of 0.1
m
/s by means of
a differential drive system.
4.3 Controller
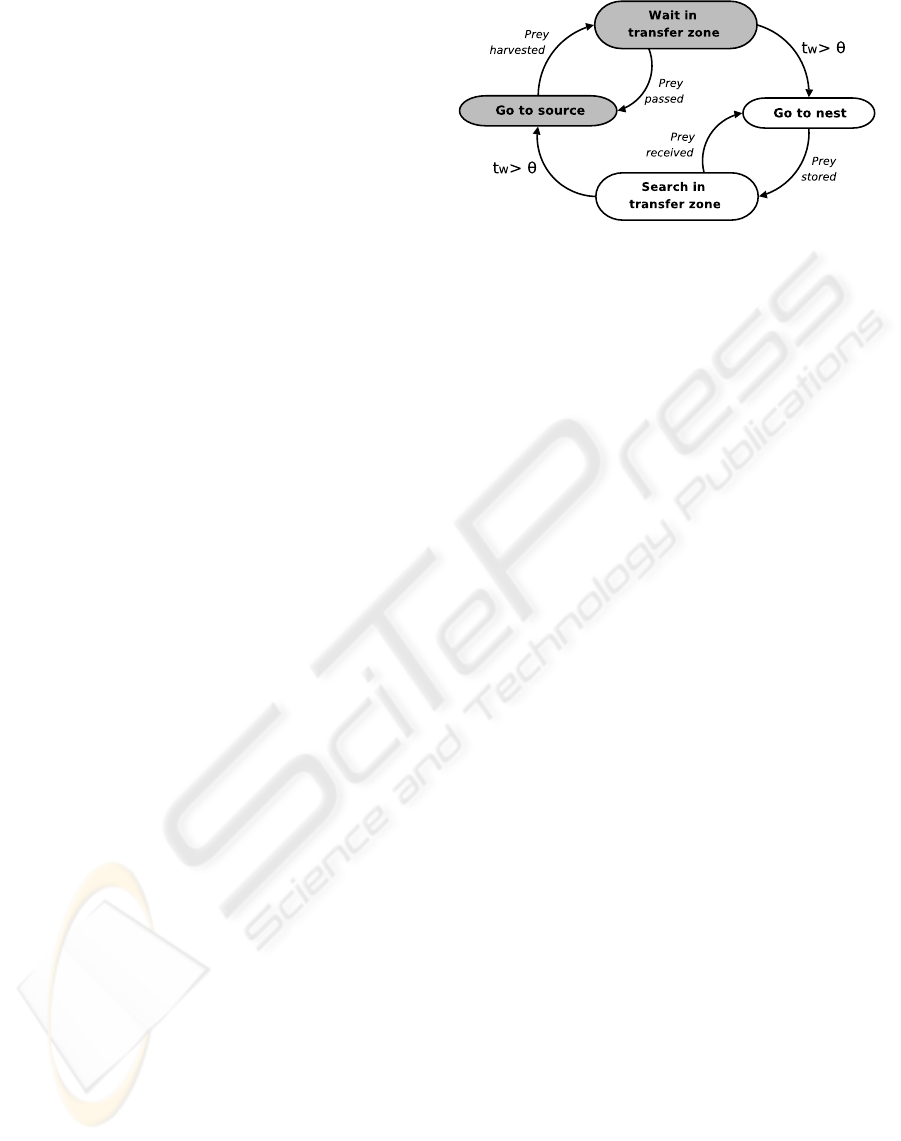
All the robots share the same, hand coded, finite state
machine controller depicted in Figure 2. The con-
troller consists of two parts, each corresponding to a
possible subtask a robot can perform. Gray states re-
fer to the harvest subtask, white states to the store
subtask. Since all the robots start in the harvest
area, their controller is initially set to perform anti-
phototaxis. In this way they will reach the source,
where they can start retrieving prey objects. The be-
havior of each robot is a function of the task it is per-
forming. Harvesters not carrying a prey object move
towards the source, where they can find prey. Har-
vesters carrying a prey object, move to the exchange
zone and wait for a free storer. Upon arrival of such
a storer, the harvester passes the prey object to it.
Storers carrying a prey object move towards the nest,
where they can deposit the object. Storers not car-
rying a prey object head to the exchange zone and
search for a harvester with a prey object. Robots can
detect other robots carrying a prey on the basis of the
color of their LED ring. While moving, each robot
avoids obstacles (walls and other robots).
Task switches can occur: a harvester carrying a
prey object can decide to become a storer, and a storer
not carrying a prey object can decide to become a har-
vester. As mentioned before, robots switch task de-
pending on an internal threshold Θ, representing the
maximum amount of control cycles they can spend in
the transfer zone waiting to pass (harvesters) or re-
ceive (storers) a prey object. If a robot remains in the
transfer zone longer than its threshold without pass-
ing or receiving prey objects (t
w
> Θ), it switches its
task. The optimal threshold value is not trivial to de-
termine. In the work presented here, we use a sim-
ple method to set the threshold Θ: at the beginning
of the experiment, each robot draws a random thresh-
old, sampled uniformly in the interval [0, 1000]. We
chose this method because it is independent of the en-
vironment and does not rely on complex approxima-
tion techniques. The threshold value does not change
during the experiment. In case of the non-partitioned
strategy, the threshold is set to Θ = 0, causing the
robots to switch subtask immediately as soon as they
reach the exchange zone.
Figure 2: Simplified state diagram of the controller of the
robots. Gray states belong to the harvest task, white states
to the store task. The obstacle avoidance state has been
omitted for clarity, as it is applicable in all states of the
robot. t
w
is the time spent in the exchange zone and Θ is
the threshold.
4.4 Experiments
The goal of the experiments is to investigate whether
task partitioning can reduce interference in task-
critical zones, and how to allocate a robotic swarm to
partitions. As pointed out by (Lerman and Galstyan,
2002), interference is related to the number of indi-
viduals in the system. Additionally, the physical in-
terference between robots is also a function of the en-
vironment the robots act in. The higher the group size,
the higher the density, resulting in a higher amount of
physical interference. Thus, in order to study interfer-
ence in our experiments, we increase the size of the
group in each of the two environments shown in Fig-
ure 1, while using both strategies (non-partitioned and
partitioned). We study the performance of the system
when the group size N ranges in the interval [1,40].
We run 50 repetitions for each value of N and each
experimental settin.
4.5 Metrics
In order to quantify the influence of interference, we
measure the group performance P by the number of
prey objects collected by the swarm at the end of the
experiment (t
max
= 1 hour). From the group perfor-
mance measure we can derive the individual efficiency
as follows:
I
eff
= P/N, (1)
where N is the size of the group. Individual efficiency
can help to understand the effect of interference on
the performance.
In order to measure the influence of environmen-
tal features on the interference, we define an inter-
ference measure taking inspiration from (Rosenfeld
et al., 2005). In their work, interference is measured
INTERFERENCE REDUCTION THROUGH TASK PARTITIONING IN A ROBOTIC SWARM - Or: "Don't you Step
on My Blue Suede Shoes!"
55
0 10 20 30 40
0 100 200 300 400
Prey objects retrieved (P)
●
non−partitioned
partitioned
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
0 10 20 30 40 50
Number of robots (N)
Prey objects retrieved
by individual robot (I
eff
)
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
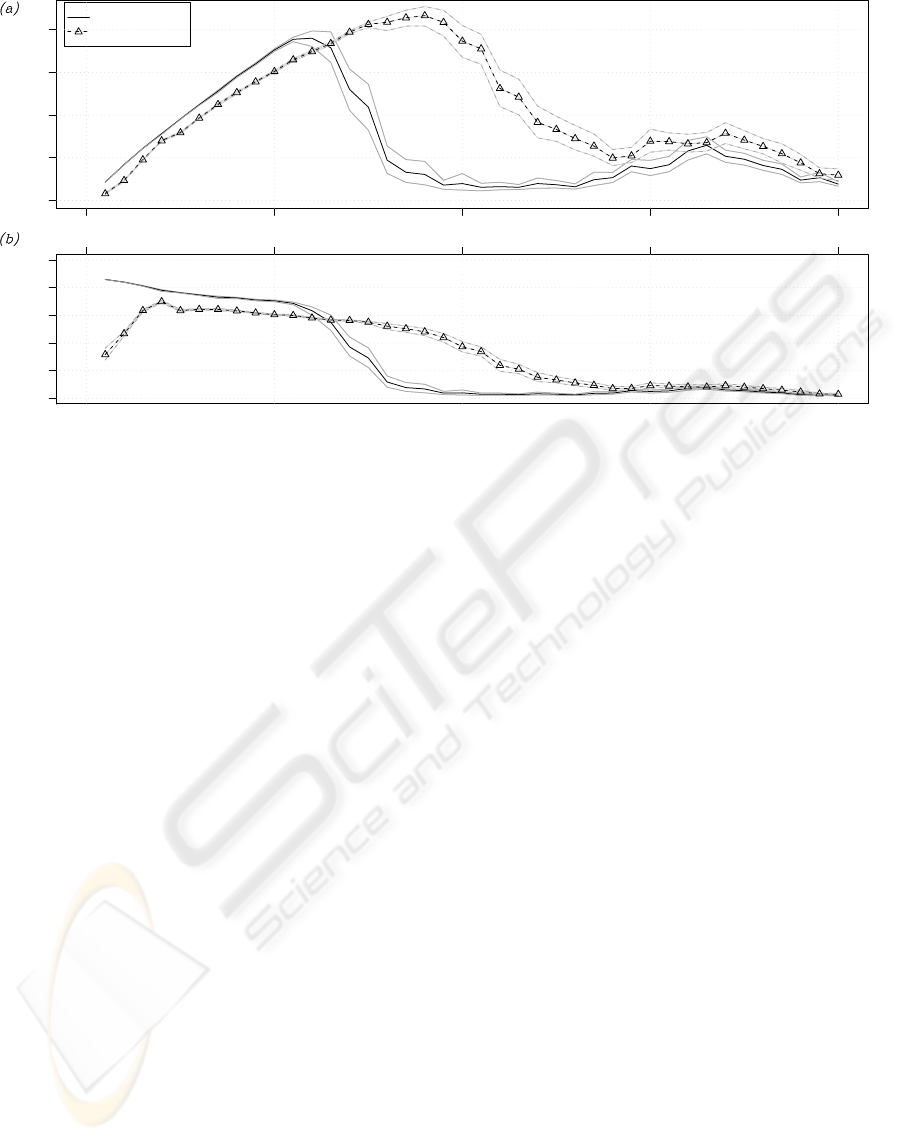
Figure 3: (a) Performance P and (b) individual efficiency I
eff
for increasing number of robots in the narrow-nest environment.
The black continuous line refers to the case of no task partitioning, the black dashed line to the case of partitioning. Gray
lines indicate the 95% confidence interval on the expected value.
as the time spent performing actions not strictly re-
lated to the task, but rather lost due to negative inter-
actions with the environment (e.g., obstacle avoidance
maneuvers). By registering the number of collisions
for each area of the arena, we can draw conclusions
about where physical interferences happen most of-
ten. We measure interference through the state of the
controller: in our case a robot is experiencing inter-
ference each time its controller perceives an obstacle.
In case of a partitioned task, there is another
source of inefficiency that adds to interference: the
time lost in the exchange zone. We define the strat-
egy cost C as the sum of time lost because of physical
interference and time lost in the exchange zone:
C = T
int
+ T
part
, (2)
where T
int
is the amount of time steps during which
the controller perceives an obstacle, and T
part
is the
total amount of time steps spent in prey passing
maneuvers. By using this metric, the cost of the
non-partitioned strategy is purely due to interference
(T
part
= 0), while in case of the partitioned strategy,
prey passing costs add to interference costs. In a way,
passing a prey object produces another kind of inter-
ference in the system. The strategy cost captures this
effect, thus allowing for a comparison of strategies.
5 RESULTS AND DISCUSSION
The graphs in Figures 3a and 4 show the perfor-
mance P for different group sizes in the narrow-nest
and wide-nest environment respectively. Figure 3b
shows the individual efficiency I
eff
of the robots in
the narrow-nest environment. Black curves are the
average computed over the 50 repetitions of each set-
ting, gray curves indicate the 95% confidence inter-
val on the expected value. The performance graph
in Figure 3a shows that the partitioned strategy im-
proves performance in the narrow-nest environment.
The graph shows that the non-partitioned strategy per-
forms better than the partitioned strategy for small
group sizes (up to N = 13 robots). However, increas-
ing the group size makes the non-partitioned strategy
collapse: the number of gathered prey objects drops
dramatically for groups larger than 13. The individual
efficiency graph (Figure 3b) can explain the behavior
of the system. The robots employing the partitioned
strategy are less efficient, for small group sizes, than
those performing the non-partitioned strategy. How-
ever, the addition of more individuals affects the ef-
ficiency of the non-partitioned group in a more dra-
matic way. At a certain point, the drop in efficiency
becomes very steep for the non-partitioned strategy.
On the other hand, the partitioned strategy scales bet-
ter: individual efficiency drops smoothly. This ex-
plains why a group using the partitioned strategy per-
forms better: it can benefit from the work of more
individuals and therefore collects more prey objects.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
56

0 10 20 30 40
0 200 400 600 800
Number of robots (N)
Prey objects retrieved (P)
●
non−partitioned
partitioned
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
Figure 4: Performance P for increasing number of robots in the wide-nest environment. The black continuous line refers
to the case of no task partitioning, the black dashed line to the case of partitioning. Gray lines indicate the 95% confidence
interval on the expected value.
Strategy cost (C)
0 5000 10000 15000 20000
Collision costs
Partition costs
Strategy cost (C)
0 5000 10000 15000 20000
0 5 10 15 20 25 30 35 40
Number of robots (N)
partitioned strategy
non−partitioned strategy
Figure 5: Cost of interference in the narrow-nest environ-
ment. Bars represent the cost C, sum of interference time
T
int
and partition time T
part
(i.e., waiting times). For easy
reference, the outline of the bars of the respective other
graph has been added to each graph. (a) Costs for the par-
titioned strategy, where interference cost stem from waiting
times and collisions. (b) Cost in case of the non-partitioned
strategy, where only physical interference through colli-
sions exists.
These considerations do not hold in the wide-nest en-
vironment. The performance graph in Figure 4 shows
that the non-partitioned strategy performs better than
the partitioned strategy for group sizes N < 33. In
both the environments, independently of the strat-
egy used to accomplish the task, the system collapses
when the area is saturated by the swarm.
Figure 5 shows the effect on the cost of increas-
ing the number of robots in the narrow-nest environ-
ment. The graph compares the cost C of each of the
two strategies for different group sizes. In case of the
partitioned strategy (Figure 5a), the graph shows each
component of the cost (T
int
and T
part
). Clearly, task
partitioning has the effect of reducing the cost due
to interference but has the disadvantage of increasing
the cost due to time lost. The probability of two or
more robots encountering each other increases with
the robot density. Although this determines a higher
interference cost (i.e., T
int
), it decreases the cost due to
lower waiting time (i.e., T
part
) in the case of the parti-
tioned strategy. Partitioning performs better when the
gain from interference reduction is greater than the
loss of performance due to partitioning inefficiencies.
These considerations hold in the narrow-nest environ-
ment, where the likelihood of physical interference in
a task-critical zone is very high. In the wide-nest en-
vironment, interference in the nest is as likely as inter-
ference in the exchange zone. Thus, it is not benefi-
cial to pay the cost of waiting and the non-partitioned
strategy performs better for any group size.
The mechanism by which partitioning reduces in-
terference costs can be deduced by comparing the in-
terference graphs in Figure 6. The graphs show the
number of times that physical interference (as de-
fined in Section 4.5) was registered in each region
of the narrow-nest environment. The total area was
discretized in squares of 1 cm
2
. Figure 6 shows the
results obtained with 18 robots, in the case of the
non-partitioned strategy (Figure 6a) and in the case
of the partitioned strategy (Figure 6b). The graphs
show that the use of the non-partitioned strategy leads
to high interference in the nest, which becomes con-
INTERFERENCE REDUCTION THROUGH TASK PARTITIONING IN A ROBOTIC SWARM - Or: "Don't you Step
on My Blue Suede Shoes!"
57

x
−2
−1
0
1
y
−0.5
0.0
0.5
Interference
0
20
40
60
80
100
partitioned
strategy
x
−2
−1
0
1
y
−0.5
0.0
0.5
Interference
0
20
40
60
80
100
non−partitioned
strategy
Figure 6: Mean interference values registered for (a) the partitioned strategy and (b) the non-partitioned strategy, both in the
narrow-nest environment. Shown values are observation means of 50 repetitions with N = 18 robots. Coordinates on the x-
and y-axis are given in meters. The arena is stretched along the y-axis for better visualization. The dashed white line marks
the location of the exchange zone.
gested. Partitioning the task reduces the robot den-
sity in the nest, thus spreading the interference more
uniformly across the arena. In addition, the overall
interference diminishes because the exchange zone is
wider: the robots have more freedom of movement
and collide less often. Although the graphs show only
data collected with 18 robots, experiments with dif-
ferent group sizes produced similar results.
6 CONCLUSIONS AND FUTURE
WORK
Interference can be an issue when working with
swarms of robots. In this work, we used task parti-
tioning and allocation to reduce interference between
robots sharing the same physical space. We manu-
ally partitioned the environment and employed a sim-
ple self-organized strategy for allocating individuals
to subtasks. Results show that a partitioning strategy
improves performance in a constrained environment.
Additionally, we identified cases in which partition-
ing is not advantageous and a non-partitioned strategy
should be used. The proposed strategy is fairly simple
and far from being an optimal solution, nevertheless
we improved the performance of the swarm when in-
terference was costly.
Future work will concern the identification of the
optimal allocation in the studied environments as well
as the development and study of a strategy that can
find this optimal allocation in a self-organized and
adaptive way. In addition, the interference metric pro-
posed in Section 4.5 could be used by the robots to
decide whether to partition the task. In this way, we
could achieve even better performance, since parti-
tioning would be employed only when strictly needed.
Finally, the goal is to validate the system using the
real robots.
ACKNOWLEDGEMENTS
This work was supported by the SWARMANOID
project, funded by the Future and Emerging Tech-
nologies programme (IST-FET) of the European
Commission, under grant IST-022888 and by the
VIRTUAL SWARMANOID project funded by the
Fund for Scientific Research F.R.S.–FNRS of Bel-
gium’s French Community. The information provided
is the sole responsibility of the authors and does not
reflect the European Commission’s opinion. The Eu-
ropean Commission is not responsible for any use that
might be made of data appearing in this publication.
Marco Dorigo and Mauro Birattari acknowledge sup-
port from the Fund for Scientific Research F.R.S.–
FNRS of Belgium’s French Community, of which
they are a research director and a research associate,
respectively.
REFERENCES
Campo, A. and Dorigo, M. (2007). Efficient multi-foraging
in swarm robotics. In Advances in Artificial Life: Pro-
ceedings of the VIIIth European Conference on Artifi-
cial Life, Lecture Notes in Artificial Intelligence LNAI
4648, pages 696–705, Berlin, Germany. Springer Ver-
lag.
Font
´
an, M. S. and Matari
´
c, M. J. (1996). A study of territo-
riality: The role of critical mass in adaptive task divi-
sion. In From Animals to Animats 4: Proceedings of
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
58

the Fourth International Conference of Simulation of
Adaptive Behavior, pages 553–561, Cambridge, MA.
MIT Press.
Gerkey, B. P. and Matari
´
c, M. J. (2004). A formal analysis
and taxonomy of task allocation in multi-robot sys-
tems. The International Journal of Robotics Research,
23(9):939–954.
Goldberg, D. (2001). Evaluating the Dynamics of Agent-
Environment Interaction. PhD thesis, University of
Southern California, Los Angeles, CA.
Goldberg, D. and Matari
´
c, M. J. (2003). Maximizing reward
in a non-stationary mobile robot environment. Au-
tonomous Agents and Multi-Agent Systems, 6(3):287–
316.
Groß, R., Bonani, M., Mondada, F., and Dorigo, M. (2006).
Autonomous self-assembly in swarm-bots. IEEE
Transactions on Robotics, 22(6):1115–1130.
Kalra, N. and Martinoli, A. (2006). A comparative study
of market-based and threshold-based task allocation.
In Proceedings of the 8th International Symposium
on Distributed Autonomous Robotic Systems (DARS),
Minneapolis, Minnesota, USA.
Krieger, M. J. B. and Billeter, J.-B. (2000). The call of
duty: Self-organised task allocation in a population of
up to twelve mobile robots. Journal of Robotics and
Autonomous Systems, 30:65–84.
Labella, T. H., Dorigo, M., and Deneubourg, J.-L. (2006).
Division of labor in a group of robots inspired by ants’
foraging behavior. ACM Transactions on Autonomous
and Adaptive Systems, 1(1):4–25.
Lein, A. and Vaughan, R. (2008). Adaptive multi-robot
bucket brigade foraging. In Proceedings of the
Eleventh International Conference on Artificial Life
(ALife XI), pages 337–342, Cambridge, MA. MIT
Press.
Lerman, K. and Galstyan, A. (2002). Mathematical model
of foraging in a group of robots: Effect of interference.
Auton. Robots, 13(2):127–141.
Liu, W., Winfield, A., Sa, J., Chen, J., and Dou, L. (2007).
Towards energy optimization: Emergent task alloca-
tion in a swarm of foraging robots. Adaptive Behavior,
15(3):289–305.
Mondada, F., Pettinaro, G. C., Guignard, A., Kwee, I. V.,
Floreano, D., Deneubourg, J.-L., Nolfi, S., Gam-
bardella, L. M., and Dorigo, M. (2004). SWARM-
BOT: A new distributed robotic concept. Autonomous
Robots, 17(2–3):193–221.
Nouyan, S., Campo, A., and Dorigo, M. (2008). Path for-
mation in a robot swarm. Self-organized strategies to
find your way home. Swarm Intelligence, 2(1):1–23.
Rosenfeld, A., Kaminka, G. A., and Kraus, S. (2005). A
study of scalability properties in robotic teams. In Co-
ordination of Large-Scale Multiagent Systems, pages
27–51, New York. Springer Verlag.
Shell, D. and Matari
´
c, M. J. (2006). On foraging strate-
gies for large-scale multi-robot systems. In Intelligent
Robots and Systems, 2006 IEEE/RSJ International
Conference on, pages 2717–2723, Beijing, China.
INTERFERENCE REDUCTION THROUGH TASK PARTITIONING IN A ROBOTIC SWARM - Or: "Don't you Step
on My Blue Suede Shoes!"
59
