NOISE POWER ESTIMATION USING RAPID ADAPTATION AND

RECURSIVE SMOOTHING PRINCIPLES

Franc¸ois Xavier Nsabimana, Udo Z

olzer

Department of Signal Processing and Communications, Helmut Schmidt University

Holstenhofweg 85, 22043 Hamburg, Germany

Vignesh Subbaraman

Information and Communication Systems, Technische Universit

at Hamburg-Harburg

Schwarzenbergstr. 95, 21073 Hamburg, Germany

Keywords:

Noise estimation, Recursive averaging, Speech presence probability, Smoothing, Bias correction and normal-

ized mean square error.

Abstract:

In this paper we present an algorithm for the robust estimation of the noise power from the speech signals

contaminated by high non stationary noise sources for speech enhancement. The noise power is ﬁrst estimated

by minimum statistics principles with a very short window. From the resulting noise power excess, the over-

estimation is accounted for using recursive averaging techniques. The performance of the proposed technique

is ﬁnally compared with the different existing approaches using various grading tests.

1 INTRODUCTION

Speech Enhancement is a technique to improve the

quality as well as the intelligibility of the corrupted

speech. The improvement of quality and intelligibil-

ity is very important because it provides accurate in-

formation exchange and contributes to reduce listener

fatigue in highly disturbed environments. In order to

enhance a corrupted speech, two activities need to be

done ﬁrst. These are noise estimation and noise re-

duction techniques. In this paper an algorithm for

the noise estimation technique is proposed. Basically

the noise estimators can be classiﬁed into two types

(Loizou, 2007). These are minima tracking and re-

cursive averaging algorithms.

In minima tracking algorithms, the spectral mini-

mum is continuously updated or tracks within a ﬁnite

window. Optimal Smoothing and Minimum statistics

algorithm is an example for the minima tracking type

(Martin, 2001). In recursive averaging algorithms the

noise power in the individual bands is updated recur-

sively, whenever the probability of speech presence is

very low. Minima controlled and recursive averaging

for robust speech enhancement (Cohen and Berdugo,

2002) and Rapid adaptation for highly non stationary

environments (Rangachari and Loizou, 2006) are ex-

amples for the recursive averaging type.

There are also several noise estimation techniques

proposed in literature (Martin, 1994; Cohen, 2003;

Rangachari et al., 2004; Erkelens and Heusdens,

2008a; Erkelens and Heusdens, 2008b). Continuous

Spectral Minima Tracking in Subbands (SMTS) pro-

posed by Doblinger (Doblinger, 1995) is one of the

classical noise estimation technique. It is very sim-

ple but its performance suffers from pronounced over-

estimation. Optimal Smoothing and Minimum Stati-

stics (OSMS) proposed by Martin (Martin, 2001) is

one of the most commonly used algorithms for noise

estimation in speech enhancement techniques. The

noise power estimated by this approach is very good

but the algorithm fails to track quickly the rapid in-

crease of the noise power in the corrupted speech.

Rapid Adaptation for Highly Non-Stationary Envi-

ronments (RAHNSE) as proposed by Loizou (Ran-

gachari and Loizou, 2006) tracks quickly the sudden

changes in the noise power. But this algorithm still

suffers from some overestimation, as it partially relies

on the SMTS approach.

The motivation for this new algorithm is to have

a noise estimator which provides a minimum overes-

timation and a small adaptation time for increasing

noise power. In this work a method to update the

noise power recursively with minimum speech leak-

age is proposed. The adaptation time of this approach

is comparable to the one of RAHNSE (0.5 sec). The

objective grading tests and the subjective spectrogram

Xavier Nsabimana F., Zölzer U. and Subbaraman V. (2009).

NOISE POWER ESTIMATION USING RAPID ADAPTATION AND RECURSIVE SMOOTHING PRINCIPLES.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 13-18

DOI: 10.5220/0002197100130018

 SciTePress

comparison reveal that the proposed algorithm per-

forms better than the simulated OSMS and RAHNSE

approaches.

The rest of paper is organised as follows. Sec-

tion 2 presents some preliminary deﬁnitions. Section

3 discusses the proposed noise estimation algorithm.

Section 4 compares the proposed technique with the

two existing approaches and Section 5 concludes.

2 PRELIMINARY DEFINITIONS

Let consider the spectrum of a corrupted speech sig-

nal to be deﬁned as

X(k, m) = S(k, m)+N(k, m), (1)

where S(k, m) and N(k, m) are the short-time DFT

coefﬁcients at frequency bin k and frame number m

from the clean speech and additive noise respectively.

S(k, m) and N(k, m) are assumed to be statistically in-

dependent and zero mean. The adjacent frames of the

corrupted speech x(n) overlap by 75 % in time do-

main.

The power level of the clean speech R

(k, m), of

the additive true noise R

(k, m) and of the corrupted

speech R

(k, m) are obtained by squaring their respec-

tive magnitude spectrum. In this paper an algorithm

to estimate R

(k, m) from R

(k, m) is proposed. The

estimated noise power is represented by R

˜n

(k, m).

3 PROPOSED RARS APPROACH

Figure 1 presents the ﬂow diagram of the Rapid Adap-

tation and Recursive Smoothing (RARS) which is the

proposed noise estimation technique in this paper.

In the RARS approach (s. Figure 1), ﬁrst the

noise power is estimated using Optimal Smoothing

and Minimum Statistics (OSMS) approach (Martin,

2001) with a very short window. This yields an over-

estimation of the estimated noise power. Based on

the smoothed posteriori SNR from the OSMS noise

power a VAD index I is derived to compute the speech

presence probability P and a smoothing parameter η.

This smoothing parameter is ﬁnally applied to the

unbiased estimated noise power R

from OSMS ap-

proach to account for the overestimation. In order to

improve the adaptation time for the estimated noise

power, a condition BC is used to track quickly the

fast changes in the noise power. The proposed al-

gorithm is not an optimal solution, yet practically it

gives very good results. Optimization of the proposed

approach is possible. In the followings the main steps

Figure 1: RARS approach. Power Spectrum Smoothing

(PSS), Bias Correction (BC), Noise Update (NU), Smooth-

ing Parameter (SP), Speech Presence Probability (SPP),

Voice Activity Detector (VAD), Smoothed SNR (SSNR).

of the RARS approach (s. Figure 1) are individual

described.

3.1 Rough Estimate with OSMS

In the ﬁrst step of the RARS approach, the noise

power is estimated using OSMS approach with very

short window length ( 0.5 - 0.6 sec). This causes

an overestimate of the noise power since the window

length is very small. The estimated noise power with

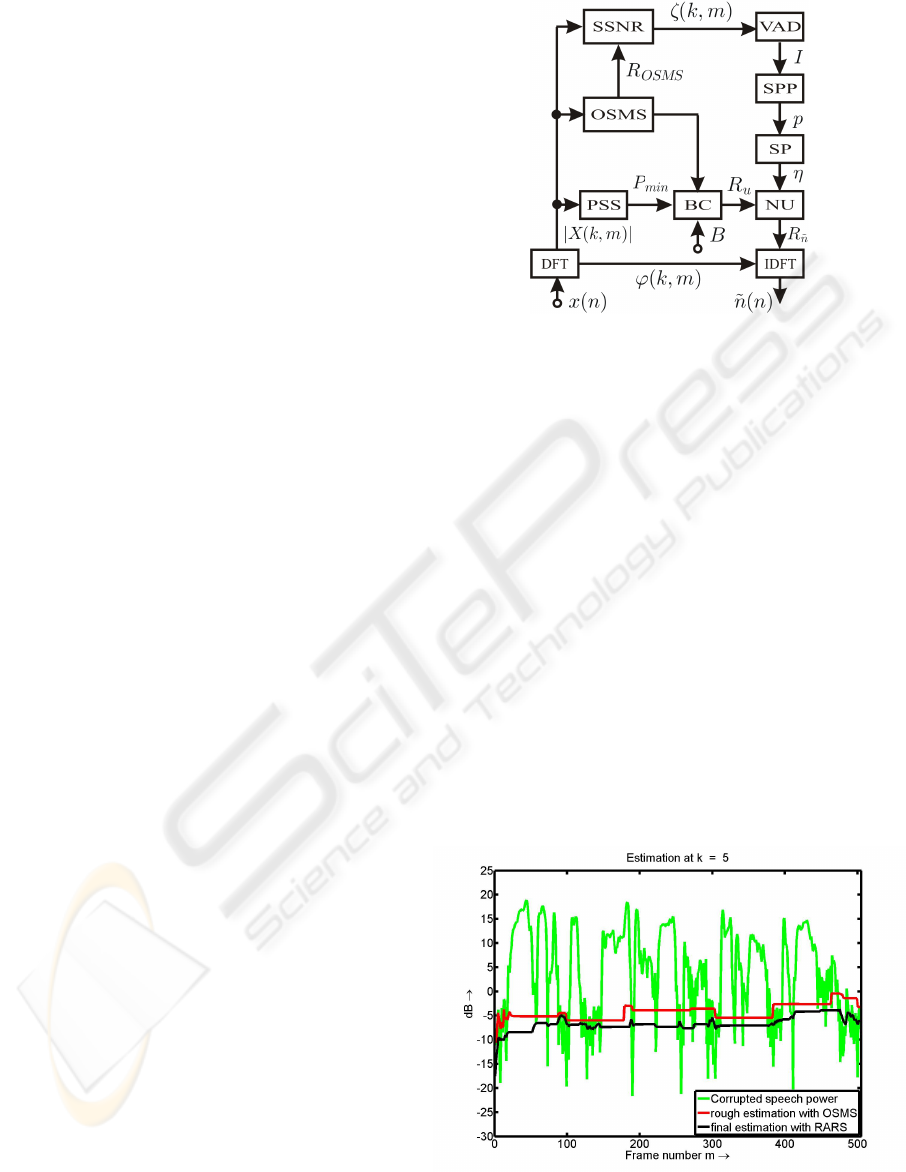
OSMS using small window and the ﬁnal estimate with

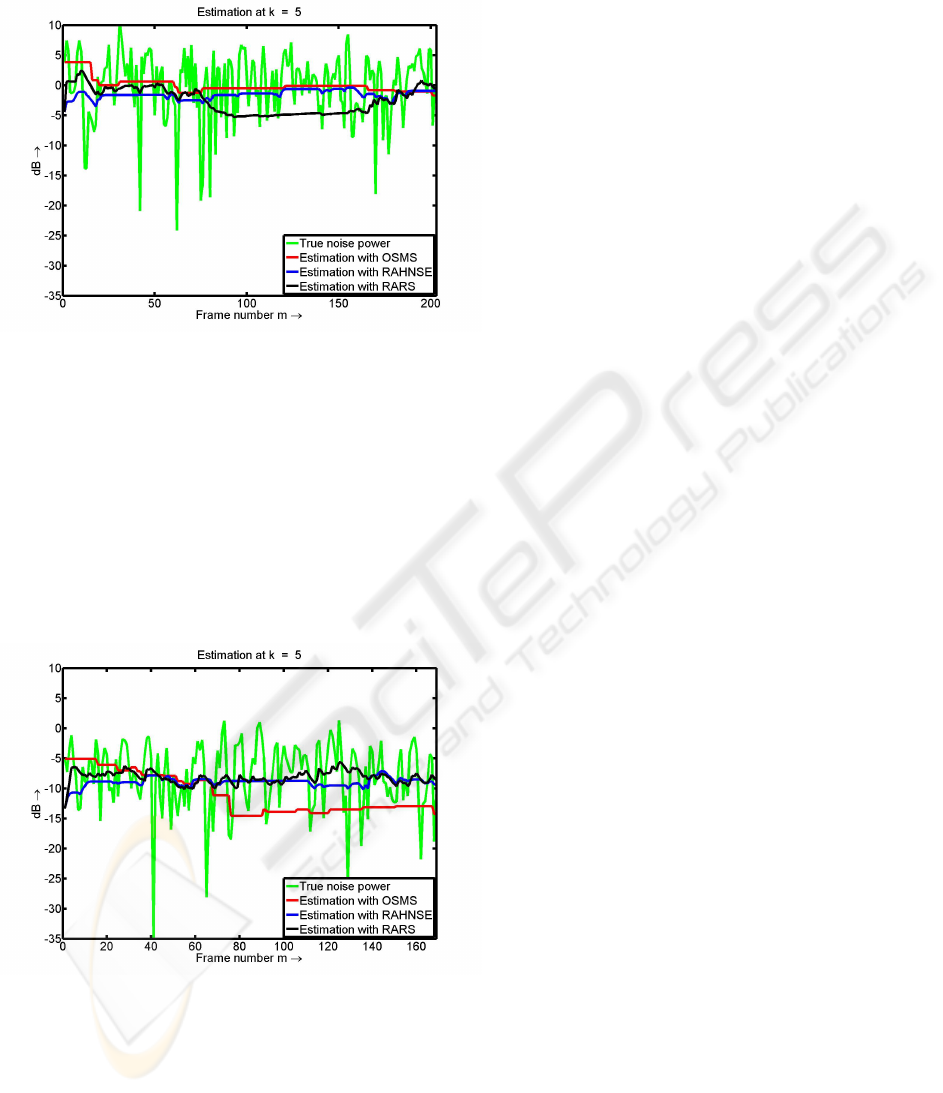
RARS can be seen in Figure 2-3, where green curve

depicts the power spectrum of the corrupted speech,

while red and black curve represent respectively the

estimated noise power with OSMS and RARS ap-

proach. From Figure 2 to Figure 3 the aforementioned

overestimation is clearly observed.

Figure 2: Rough estimate with OSMS vs. ﬁnal estimate

with RARS. Results for frequency bin k=5.

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications

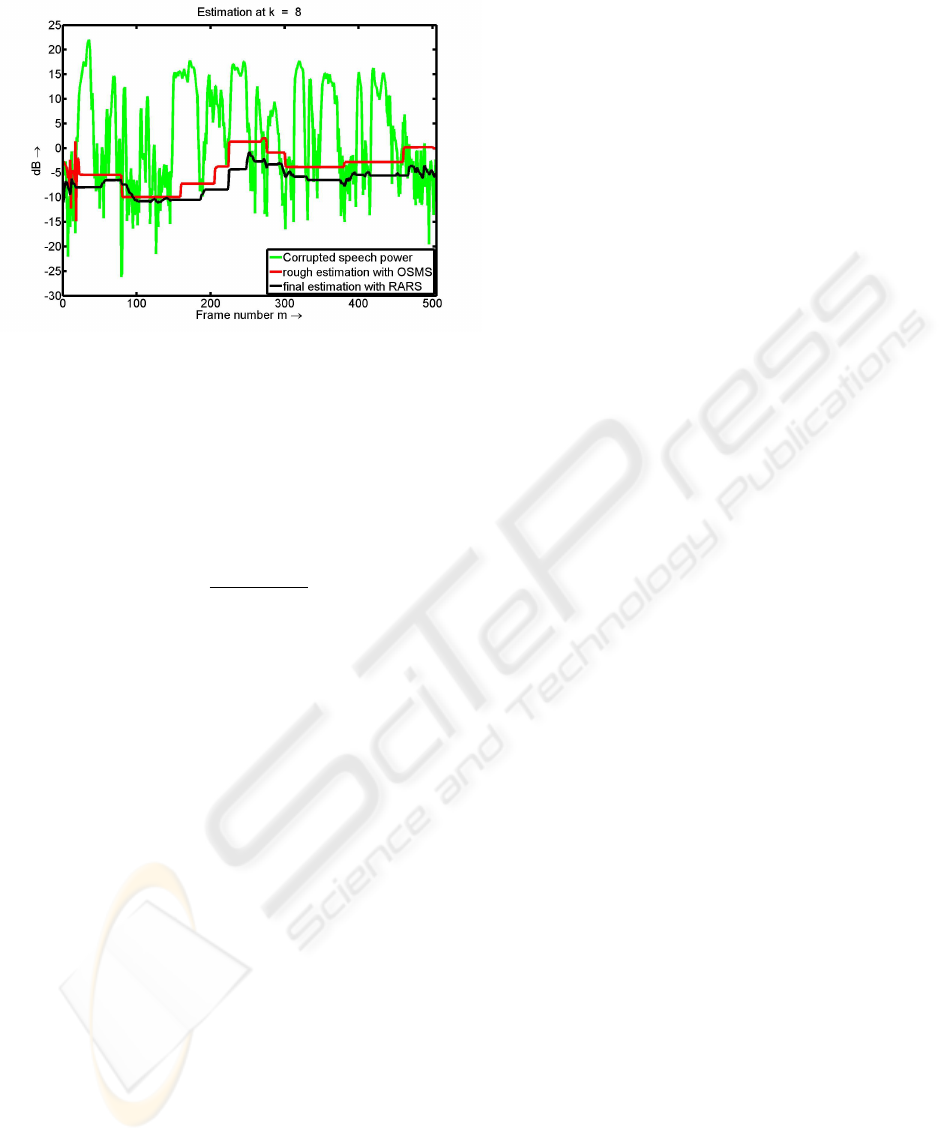
Figure 3: Rough estimate with OSMS vs. ﬁnal estimate

with RARS. Results for frequency bin k=8.

3.2 Speech Presence Probability

In order to calculate the speech presence probabil-

ity the idea proposed by Cohen (Cohen and Berdugo,

2002) is used. Firstly the a posteriori SNR is calcu-

lated using the OSMS estimated noise power as

ζ(k, m) =

(k, m)

OSMS

(k, m)

. (2)

Since ζ(k, m) is computed using overestimated noise

power, it cannot be used directly. To overcome this ef-

fect the a posteriori SNR is smoothed over the neigh-

boring frequency bins to take into account the strong

correlation of speech presence across the frequency

bins in the same frame (Cohen and Berdugo, 2002).

Smoothed SNR is given by

ζ(k, m) =

i= j

∑

i=− j

w(i) · ζ(k − i, m) (3)

where,

i= j

∑

i=− j

w(i) = 1 (4)

and 2 j + 1 is a window length for the frequency

smoothing.

ζ(k, m) is then compared with a thresh-

old ∆ to derive a VAD index I(k, m) as follows,

I(k, m) =



1 , if

ζ(k, m) > ∆

0 , otherwise,

(5)

where ∆ is an empirically determined threshold and

I(k, m) = 1 represents speech present bin. ∆ = 4.7

was proposed by Cohen (Cohen and Berdugo, 2002).

Based on the VAD index the speech presence proba-

bility is then given by

p(k, m) = γ · p(k, m − 1)+ (1 − γ) · I(k, m), (6)

where γ is a constant determined empirically. Values

of γ ≤ 0.2 are suggested for a better estimate (Cohen

and Berdugo, 2002). p(k, m) is the probability for the

bin to be speech. If I(k, m) = 1, then value of p(k, m)

increases, else if I(k, m) = 0, the value of p(k, m) de-

creases. It should be pointed out that Eq. (3) implic-

itly takes correlation of speech presence in adjacent

bins into consideration. Note also that the threshold

∆ in Eq. (5) plays an important role in speech detec-

tion. If the threshold ∆ is low, speech presence can be

detected with higher conﬁdence thus avoiding overes-

timation (Cohen and Berdugo, 2002).

3.3 Smoothing Parameter

With the help of the above derived speech presence

probability a time frequency dependent smoothing

parameter

η(k, m) = β + (1 − β) · p(k, m) (7)

is updated, where β is a constant. Values of β ≥ 0.85

yield a better estimate of η as proposed in (Cohen

and Berdugo, 2002). If p(k, m) is high, then value

of η(k, m) will be high. Else if p(k, m) is low, then

value of η(k, m) will be low. η(k, m) takes value in

the range β ≤ η(k, m) ≤ 1 . It is expected that the

smoothing parameter will be close to 1 during speech

presence regions.

3.4 Tracking Fast Changes

An algorithm to track the fast changes in noise power

is proposed here. The adaptation time for the pro-

posed algorithm is around 0.5 sec, thus close to that of

Rapid Adaption for Highly Non-Stationary Environ-

ments (RAHNSE approach) (Rangachari and Loizou,

2006). A simple and effective idea as proposed

in (Erkelens and Heusdens, 2008a) is applied here,

which ensures that the proposed approach can track

quickly changes in the noise power. First a refer-

ence noise power estimate using OSMS with a short

window (0.5 sec) is computed. The corrupted speech

power is smoothed with a low value smoothing con-

stant. The idea here is to push the noise estimate

into the right direction when there is an increase in

noise power. The smoothed corrupted speech power

is given by

P(k, m) = α · P(k − 1, m)+(1 − α) · R

(k, m), (8)

where values of α ≤ 0.2 are suggested for better

smoothing. From the smoothed power spectrum,

min

is found for a window length of at least 0.5

sec. Because of small smoothing constant, smoothed

spectrum power almost follows the corrupted speech

NOISE POWER ESTIMATION USING RAPID ADAPTATION AND RECURSIVE SMOOTHING PRINCIPLES

power. To account for biased estimate the following

condition

if BP

min

(k, m) > R

OSMS

(k, m), then

(k, m) = BP

min

(k, m) (9)

is tested, where B > 1 is a bias correction factor. For

the RARS approach B = 1.5 yields good bias cor-

rection. If the above condition fails then R

(k, m) =

OSMS

(k, m). In case of increase in noise power

min

(k, m) will be greater than R

OSMS

(k, m). The

value for R

OSMS

(k, m) is thus replaced by BP

min

(k, m).

For this case the probability is updated to p(k, m) = 0

and the smoothing parameter for noise update is then

recomputed (s. Eq. (7)). Observations (Erkelens and

Heusdens, 2008a) reveal that the value of B and win-

dow length is not critical, but a window length of at

least 0.5 sec is necessary for good performances.

3.5 Noise Power Update

Finally with the frequency dependent smoothing fac-

tor η(k, m) from Eq. (7), the spectral noise power

from RARS approach is updated using

˜n

(k, m) = η· R

˜n

(k, m− 1)+ (1− η)· R

(k, m). (10)

The key idea of this algorithm is that instead of

using the corrupted speech power R

(k, m) to updated

the noise estimate (Rangachari and Loizou, 2006),

the unbiased estimate R

of noise power from OSMS

algorithm is used. Since R

(k, m) has minimum

speech power as compared to corrupted speech power

(k, m), the speech power leakage into noise power

in this approach is minimized. Whenever the speech

presence probability is low, the estimated noise power

will follow R

(k, m). But when the speech presence

probability is high, estimated noise power will follow

the noise power in the previous frame. Thus, as shown

in Figure 3, the proposed algorithm avoids the over-

estimated values observed in the rough OSMS esti-

mation from Figure 2.

4 SIMULATION RESULTS

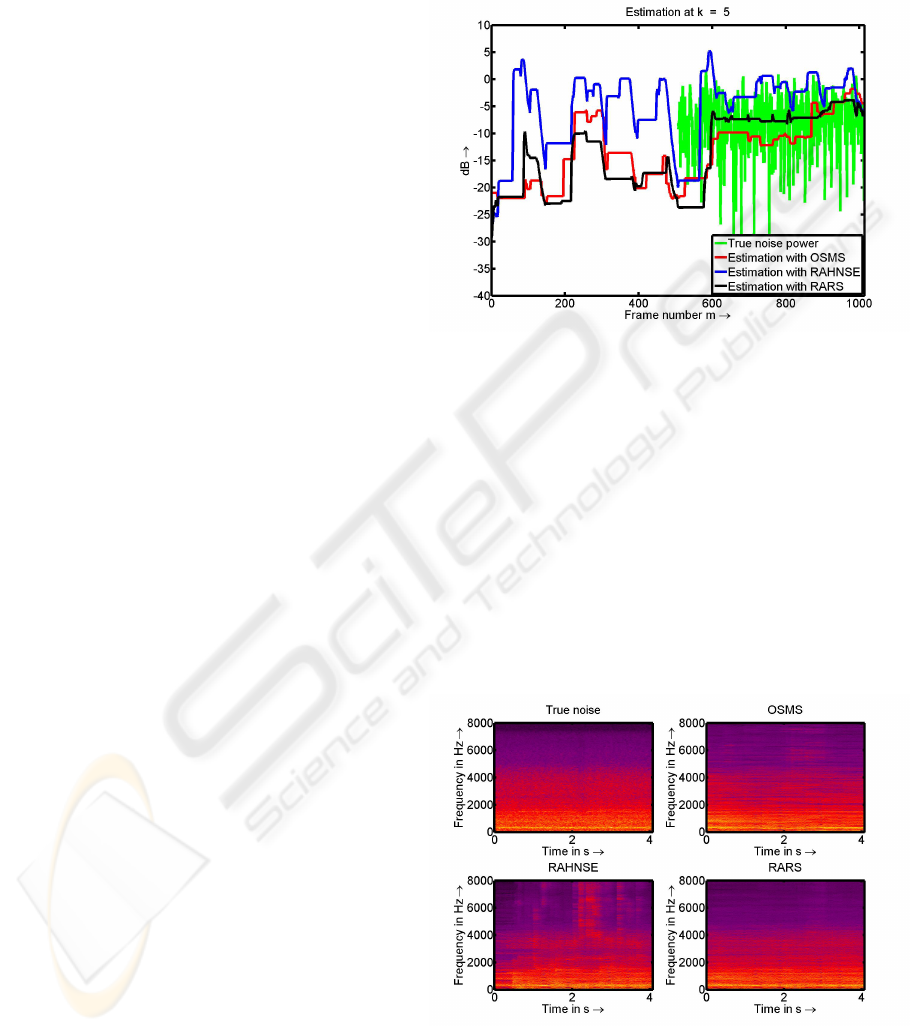
Figure 4 presents the comparison between OSMS,

RAHNSE and RARS approach in terms of rapid

adaption and true minimum estimate. This simula-

tion was run for a mixed signal where the ﬁrst 500

frames consist of only clean speech and the last 500

frames consist of the same clean speech but corrupted

with car noise at 5 dB SNR. The estimation for both

parts of the mixed signal reveals the best minimum

estimate for the RARS approach followed by OSMS.

Best rapid adaptation is observed by RAHNSE fol-

lowed by RARS approach. The adaptation time for

the proposed approach is also around 0.5 to 0.6 sec

as in RAHNSE approach. A comparison at only

Figure 4: Comparison in terms of true noise estimate and

rapid adaptation time. True car noise (green), RAHNSE

(blue), OSMS (red) and RARS (black).

one speciﬁed frequency bin may not be sufﬁcient to

state about the performances of the three approaches.

Figure 5 thus presents a subjective study of the esti-

mated noise in terms of spectrograms. Obviously the

result with the RARS approach (s. Figure 5 lower plot

right) is close to the true noise (s. Figure 5 upper plot

left). Some pronounced overestimations are observed

in the RAHNSE approach (s. Figure 5 lower plot left)

especially for high frequency bands. The OSMS re-

sult in Figure 5 upper plot right can be found close to

the RARS result than to the RAHNSE one.

Figure 5: Subjective study of spectrograms for the esti-

mated noise. True car noise (upper plot left), OSMS (upper

plot right), RAHNSE (lower plot left) and RARS (lower

plot right).

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications

4.1 Normalized Mean Square Error

The results obtained for the estimated noise with three

compared approaches have been graded also in terms

of Normalized Mean Square Error (NMSE) given by

NMSE =

M−1

∑

m=0

L−1

∑

k=0

(k, m)− R

˜n

(k, m)]

L−1

∑

k=0

(k, m)]

, (11)

where R

(k, m) is the true noise power and R

˜n

(k, m)

represents the estimated noise power. Ideally the

value for NMSE lies in the interval [0 1], where 0

represents true estimation and 1 represents very poor

estimation. But practically the NMSE value can be

greater than 1 due to overestimation. Whenever there

is an overestimation in the algorithm, the value for

˜n

(k, m) can be twice greater than R

(k, m) therefore

the ratio in Eq. (11) can be greater than 1. All the sig-

nals used for the simulation in this paper are from the

Noisex-92 database taken from Sharon Gannot and

Peter Vary web pages. Table 1 to 3 show NMSE re-

sults for three kinds of corrupting noise. These results

reveal that the RARS approach is graded best.

Table 1: NMSE for the estimated noise power from a speech

signal corrupted by car noise at 5 dB SNR.

Algorithm NMSE

OSMS 0.740

RAHNSE 0.692

RARS 0.601

Table 2: NMSE for the estimated noise power from a speech

signal corrupted by room noise at 9 dB SNR.

Algorithm NMSE

OSMS 0.211

RAHNSE 0.391

RARS 0.061

Table 3: NMSE for the estimated noise power from a speech

signal corrupted by white noise at 9 dB SNR.

Algorithm NMSE

OSMS 0.023

RAHNSE 0.011

RARS 0.007

While Table 1 and 3 reveal that the RAHNSE ap-

proach is graded second for these two kinds of cor-

rupting noise, Table 1 clearly shows that OSMS ap-

proach remains close to RARS approach for that cor-

rupting noise. In general the NMSE values remain

close for these three approaches.

4.2 Subjective Comparison using Plots

The results of the three approaches have been also

compared subjectively in terms of plots. The follow-

ing ﬁgures presents the results of the comparison be-

tween true noise and estimated noise for speech sig-

nal corrupted by car noise at 5dB, room noise at 9

dB and white noise at 9 dB. In the following ﬁgures,

the green, red, blue and black curve represent respec-

tively the true noise power, the estimated noise power

from the OSMS, RAHNSE and RARS approaches.

For the sake of completeness, the comparison is pre-

sented for the simulation of the estimated noise power

at frequency index k = 5.

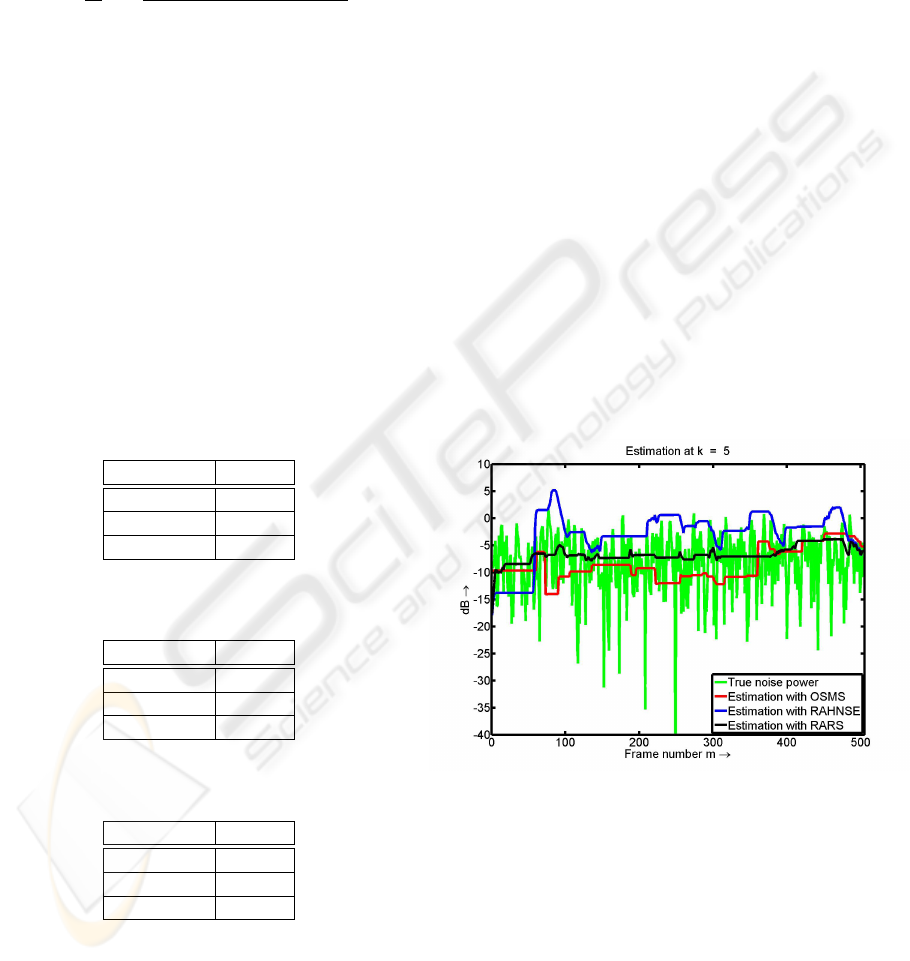
Figure 6 presents the plot of true noise power and

the estimated noise power from a speech signal cor-

rupted by car noise at 5dB. The purpose of the estima-

tor is to ﬁnd the mean value of the green curve from

the corrupted speech power. It can be noticed that the

red curve is below the mean value of the green curve.

The blue curve (noise power estimated by RAHNSE)

is instead pretty high. It clearly reveals some over-

estimation. It is obvious that the black curve (esti-

mated noise power by the RARS approach) clearly

follows here the mean of the true noise power (see

green curve).

Figure 6: Estimated noise power for speech signal corrupted

by car noise at 5dB. Results for frequency index k=5.

Figure 7 depicts the plot of true noise power

against the estimated noise power from a speech sig-

nal corrupted by room noise at 9dB at 5dB. The green

curve still represents here the true noise power. The

black curve (noise power from RARS) reveals some

underestimation of the noise power in the region of

frame number 75 to 150. Outside this region it fol-

lows the mean of the true noise power. Blue (noise

power from RAHNSE) and red curves (noise power

from OSMS) are pretty close and they follow the

NOISE POWER ESTIMATION USING RAPID ADAPTATION AND RECURSIVE SMOOTHING PRINCIPLES

mean value pretty well in this case.

Figure 7: Estimated noise power for speech signal corrupted

by room noise at 9dB. Results for frequency index k=5.

Figure 8 shows the plot of true noise power and the

estimated noise power from a speech signal corrupted

by white noise at 9dB. The green curve still depicts

here the true noise power. The red curve (noise power

from OSMS) represents the underestimated power.

Blue (noise power from RAHNSE) and Black curves

(noise power from RARS) are pretty close. But an in-

dept view states that the black curve really follows the

mean of green curve.

Figure 8: Estimated noise power for speech signal corrupted

by white noise at 9dB. Results for frequency index k=5.

5 CONCLUSIONS

A robust noise estimation technique based on mini-

mum statistics and recursive averaging is presented

here. The proposed approach (RARS) relies on the

OSMS approach with very short window. But the

RARS approach addresses the subsequent overesti-

mation and adapts fast to rapid changes in noise power

than the OSMS approach. The results of the RARS

approach has been compared to the results of OSMS

and RAHNSE approach subjectively in terms of plots

(spectrograms) and objectively in terms of NMSE. A

Comparison in terms of true noise estimate and rapid

adaptation time reveals that the RARS approach is

performing best. A subjective study of spectrograms

for the estimated noise also reveals that the RARS es-

timated noise is close to the true noise.

REFERENCES

Cohen, I. (2003). Noise spectrum estimation in adverse

environments: improved minima controlled recursive

averaging. In IEEE Trans Speech Audio Processing,

volume 411.

Cohen, I. and Berdugo, B. (2002). Noise estimation by min-

ima controlled recursive averaging for robust speech

enhancement. In IEEE Signal Proc. Letters.

Doblinger, G. (1995). Computationally efﬁcient speech en-

hancement by spectral minima tracking in subbands.

In Proc. of Eurospeech, volume 2.

Erkelens, J. and Heusdens, R. (2008a). Fast noise tracking

based on recursive smoothing of mmse noise power

estimates. In Proc. of ICASSP.

Erkelens, J. and Heusdens, R. (2008b). Tracking of non-

stationary noise based on data-driven recursive noise

power estimation. In IEEE Trans. on Audio, Speech,

and Language Processing, volume 16, pages 1112–

1123.

Loizou, P. (2007). Speech Enhancement Theory and Prac-

tice. Taylor and Francis Group, New York, 1rst edi-

tion.

Martin, R. (1994). Spectral subtraction based on minimum

statistics. In Proc. of EUSIPCO.

Martin, R. (2001). Noise power spectral density estima-

tion based on optimal smoothing and minimum statis-

tics. In IEEE Trans. on Speech, Audio Processing,

volume 9.

Rangachari, S. and Loizou, P. (2006). A noise estimation

algorithm for highly non stationary environments. In

Proc. of Speech Communications, volume 48.

Rangachari, S., Loizou, P., and Hu, Y. (2004). A noise

estimation algorithm with rapid adaptation for highly

nonstationary environments. In Proc. of ICASSP, vol-

ume 1.

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications