THE EXTRACTION OF KNOWLEDGE RULES FROM ARTIFICIAL

NEURAL NETWORKS APPLIED IN THE ELECTRIC LOAD

DEMAND FORECAST PROBLEM

How Artiﬁcial Neural Networks Retain Knowledge and Make Reliable Forecasts

Tarcisio R. Steinmetz, Adelmo L. Cechin and Jose V. Canto dos Santos

PIPCA - UNISINOS, Av. Unisinos, Sao Leopoldo, Brazil

Keywords:

Rule extraction from Artiﬁcial Neural Networks, Fuzzy Set Theory, Principal Components Analysis, Electric

Load Demand Forecast.

Abstract:

We present a methodology for the extraction of rules from Artiﬁcial Neural Networks (ANN) trained to fore-

cast the electric load demand. The rules have the ability to express the knowledge regarding the behavior of

load demand acquired by the network during training process. The rules are presented to the user in an easy

to read format, such as IF premise T HEN consequence. Where premise relates to the input data submitted

to the network (mapped as fuzzy sets), and consequence appears as a linear equation describing the output to

be presented by the network, should the premise part holds true. Experimentation demonstrates the method’s

capacity for acquiring and presenting high quality rules from neural networks trained to forecast electric load

demand for several amounts of time in the future.

1 INTRODUCTION

One important issue concerning the requirements of

proper load demand forecast methods is the ever in-

creasing dependency of electricity supply for today’s

industrial societies. Hence, the last decades have

shown large investments from energy supply compa-

nies in order to improve operation security of electric

networks and to ensure quality of service of energy

supply for the costumers (Ghods and Kalantar, 2008).

These objectives could be achieved through the use of

a better knowledge of the load demand behavior for

the area supplied by energy supply companies. Such

knowledge can even be used to guide the company’s

tactical and strategic decision making within the com-

pany’s administrative areas.

This work presents a methodology designed for

the extraction of rules form Artiﬁcial Neural Net-

works trained to forecast electric load demand for

several amounts of time in the future. The rules ob-

tained describe the knowledge acquired by the net-

work during the training phase. The rules provide

insight about the load demand behavior for the area

where the training data have been gathered (a city,

for instance), such as the impact that each of the in-

put variables cause on the load demand, under what

circumstances occurs drastic changes in the load de-

mand pattern, among other important information to

support tactical and strategic decisions throughout the

energy supply company. This paper proceeds as fol-

lows: in the next section we discuss some theoretical

aspects. Section 3 details FAGNIS, the rule extraction

method used in this work. Section 4 demonstrates the

methodology proposed for the proper rule extraction

from the trained ANNs. Section 5 shows some of the

experiments used to validate the method and the re-

sults obtained. In Section 6 we ﬁnish the document,

presenting our conclusions.

2 THEORY

This section deals with the theoretical concepts used

in this paper. Fuzzy Set Theory and Principal Com-

ponents Analysis are used in this work, however, due

to space limitations they are not covered here. The

reader should refer to (Angelov, 2002) and (Hastie

et al., 2009) to read about these topics.

2.1 Electric Load Demand Forecast

The electricity demand or system load encompasses

the summation of electric usage at each consumption

point (users) supplied by an electric supply facility.

195

R. Steinmetz T., L. Cechin A. and V. Canto dos Santos J. (2009).

THE EXTRACTION OF KNOWLEDGE RULES FROM ARTIFICIAL NEURAL NETWORKS APPLIED IN THE ELECTRIC LOAD DEMAND FORECAST

PROBLEM - How Artiﬁcial Neural Networks Retain Knowledge and Make Reliable Forecasts .

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,

pages 195-200

DOI: 10.5220/0002198201950200

 SciTePress

Its behavior is highly dynamic and difﬁcult to com-

prehend. The amount of variables involved in the

characterization of the load demand curve is large in-

deed, and different effects are perceived by the same

variables in different regions of the globe. However,

works such as (Gross and Galiana, 1987), (Srinivasan

et al., 1995), (Srinivasan et al., 1999) and (Ghods and

Kalantar, 2008) show that certain factors are com-

monly responsible for affecting the load demand.

2.2 Rule Extraction from Trained

Neural Networks

The reason for the successful application of AANs in

ﬁelds as diverse as academia, industry and commerce

is its generalization capabilities. However, this high

power of generalization comes at a price: it prevents

the network from expressing the knowledge acquired

during the training phase. Thus the network can be

seen as a black box, presenting to the user the pre-

dicted output based on the input data, while impor-

tant knowledge about the problem studied remains en-

crypted within the network’s weight matrix, never to

be discovered.

In order to solve this problem, rule extraction tech-

niques can be used to acquire the knowledge em-

bedded in the network’s weight matrix, and then to

present it to the user in a clear interface. As men-

tioned before, rules have a IF premise THEN conse-

quence structure, where premise somehow deﬁnes the

vector of input data presented to the network and con-

sequence describes the output to be obtained should

the premise part holds true. Mostly of the rule ex-

traction methods used today rely on Fuzzy Sets con-

cepts to describe the premise part of the rules (Cechin,

1998), (Benitez et al., 1997).

In an important survey concerning several rule ex-

traction methods, Andrews et al. (Andrews et al.,

1995) present several interesting features displayed

by transparent neural networks, that is, ANN capable

of describing their knowledge to the user. In this work

the authors mention that ANNs with explanatory ca-

pabilities are capable of (among others): (1) operating

in conjunction with symbolic intelligent systems; (2)

controlling critical applications such as air trafﬁc con-

trol and support scientiﬁc theory formulation.

3 FAGNIS - RULE EXTRACTION

FROM SIGMOID NETWORKS

This section describes FAGNIS (Cechin, 1998), the

rule extraction method selected for this work. FAG-

NIS has been considered because of its ability to

extract rules from standard feedforward neural net-

works, with or without shortcut connections, and

heaving one or more hidden layers. Further, since

FAGNIS performs on an already trained network, it

has no dependency on its training algorithm. In fact,

any training algorithm can be used, from the stan-

dard backpropagation to algorithms yet to be created.

Requirements such as special ANN architectures and

special or adapted learning algorithms are mandatory

in the majority of rule extraction methods, namely

(Jang et al., 1997) and (Nauck et al., 1994).

FAGNIS begins its extraction procedure by split-

ting the sigmoid curve within the hidden neurons in

three regions. These regions are then transformed in

straight lines, which are mapped by very simple equa-

tions, as illustrated in Figure 1.

Figure 1: Separation of the sigmoid curve within the hidden

neurons performed by FAGNIS.

Next, the training data are once more submitted

to the network, where FAGNIS veriﬁes the resulting

activation of the hidden neurons for each of the data

points. The data points are then grouped according to

the activation regions (as shown in Figure 1) gener-

ated within the network’s hidden neurons.

To assemble the premise part of the rules, FAG-

NIS transforms each group of data points found in the

previous step in fuzzy sets. The fuzzy sets are rep-

resented by the midpoint of each group. The conse-

quence part of the rule is deﬁned as a linear equation

that represents the output dependence of the network

on the input data. The expressions below show two

rules acquired from a ﬁctitious neural network

IF (x

, x

) is G

THEN y = x

i j

+ x

i j

+ k

IF (x

, x

) is G

THEN y = x

i j

+ x

i j

− k

where G

and G

are fuzzy sets (with membership

functions µ

and µ

respectively), w

i j

is the weight

linking the i-th neuron to the j-th neuron and k is the

intercept value for the equation.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

196

4 METHOD

The ﬁrst step of the process is to prepare the ANN

to be used as the forecaster model. Some consoli-

dated techniques, such as variable selection method

and cross-validation technique were used to improve

the model, as well as to decide on key issues concern-

ing the ANN’s architecture. The Mean Absolute Per-

centage Error (MAPE) metric was selected to mea-

sure the ANN’s accuracy, as shown in Equation (1):

MAPE =

∑

i = 1



− F



(1)

where n is the number of data points, A

is the actual

value and F

is the forecast value. Once the dataset is

composed, each data point is normalized as shown in

Equation (2):

− µ

(2)

where nd

is the normalized data, d

is the actual data

(from the dataset), µ

is the mean of the data column

and σ is the standard deviation for the data column.

Principal Components Analysis (PCA) is then ex-

ecuted on the dataset, and the resulting dataset is then

used to train the neural network. The principal com-

ponents are selected based on Jolliffe’s criterion (Jol-

liffe, 2002).

Once the neural network is properly built and

trained, FAGNIS can be used to extract knowledge

rules from it.

The algorithm is executed as detailed in Section

3. Once the execution is terminated, the rules can be

analyzed and interpreted. The equations on the con-

sequence part of the rules explain the load demand

behavior for the data assigned to the fuzzy sets de-

scribed in the premise part. To determine which of

the input variables is the most important, that is, the

one that has the major inﬂuence on the load demand,

the user needs simply to identify which of the inde-

pendent variables of the equation has the highest ab-

solute coefﬁcient value.

5 EXPERIMENTS AND RESULTS

This section describes the results obtained from two

experiments used to evaluate the proposed methodol-

ogy. The ﬁrst experiment concerns the extraction of

rules from ANN trained to predict the average load for

the next hour. In the second experiment, the forecast

window is expanded to the next month.

5.1 Experiment 1

The load demand forecast for the next hour constitutes

a classical problem within this ﬁeld, and the adoption

of neural networks techniques usually leads to excel-

lent results. Regardless of the triviality of this prob-

lem, the energy supply companies should not under-

estimate the value of such information: the load de-

mand for the next hour provides support to several of

the company’s tactical decisions like the expansion of

transmission lines, equipment maintenance schedule

and other routine activities.

The dataset used in this experiment corresponds

to the hourly load recorded from 2003 to 2007, For

a capital city holding approximately 1.4 million of

citizens. The data has been arranged in such a way

that daily, weekly, monthly and annually load pat-

terns could be learned by the neural network. The

list below represents the structure of the dataset prior

to PCA application:

• load demand for the last twenty-four hours (24

columns),

• load demand for the forecast hour registered in the

last six days (6 columns),

• load demand for the same day and forecast hour

registered in the last three weeks (3 columns),

• load demand for the forecast hour and day regis-

tered in the last month (1 column),

• dependent variable: average load demand for the

next hour.

After data processing, the principal components were

extracted. Jolliffe’s Criterion informed that the ﬁrst

eight components should be used as the input layer of

the neural network. The data belonging to the remain-

ing components were discarded from the experiment.

The neural network selected by tenfold cross-

validation method has eight neurons in the input layer,

four in the hidden layer and one in the output layer.

The network’s accuracy, measured by the MAPE met-

ric, is of 0,027%.

Some of the rules extracted by FAGNIS appear in

table 1. Not all the thirty-four rules were displayed

due to space reasons. The rules show that the three

ﬁrst principal components have an increasing effect

on the load (their coefﬁcient values are positive in all

the thirty-four rules). On the other hand, the fourth

principal component has a decreasing effect on the

load demand (it has negative coefﬁcient value in all

the rules).

The rules are arranged in the following format:

IF (PC

is F

) AND (PC

is F

) ... AND (PC

is F

)

THEN y = int + KPC

+ KPC

+ ... + KPC

THE EXTRACTION OF KNOWLEDGE RULES FROM ARTIFICIAL NEURAL NETWORKS APPLIED IN THE

ELECTRIC LOAD DEMAND FORECAST PROBLEM - How Artificial Neural Networks Retain Knowledge and Make

Reliable Forecasts

197

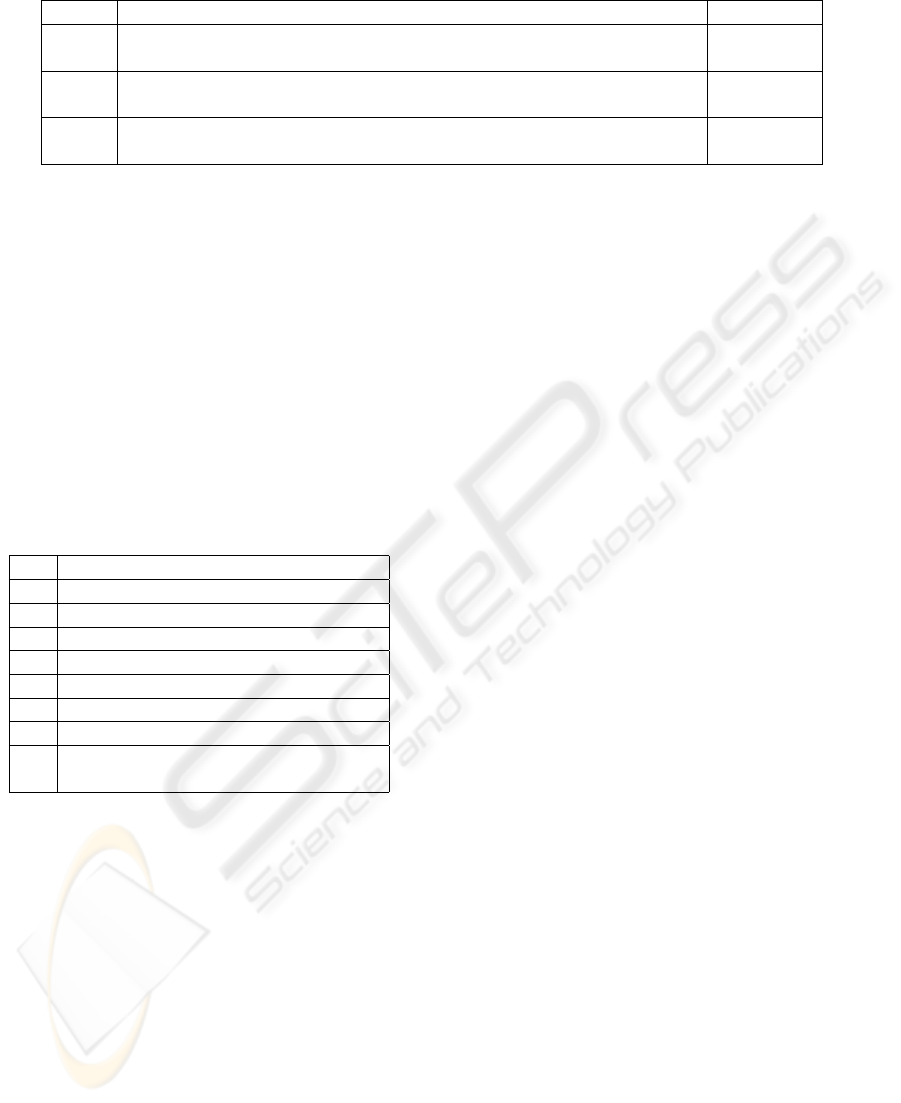
Table 1: Some of the rules found by FAGNIS in experiment 1.

Rule # Rule description Data points

1 IF x = (0.319 -1.272 -0.431 -0.091 0.275 -0.349 -0.159 -0.312) 8946

THEN y = (0.036 0.189 0.174 0.128 -0.175 0.159 0.047 0.038 -0.093)

2 IF x = (1.913 1.350 0.327 -1.651 -0.609 0.923 0.301 0.317) 3948

THEN y = (-0.004 0.208 0.191 0.179 -0.096 0.204 -0.001 0.237 0.131)

3 IF x = (1.179 -0.652 1.299 0.420 0.080 0.006 0.867 0.390) 3556

THEN y = (-0.085 0.215 0.207 0.156 -0.183 0.136 0.111 0.192 0.162)

where PC

is the principal components used as the

input layer of the neural network, F

are the fuzzy sets

representing the data being submitted to the ANN’s

input layer, K are the coefﬁcient values of the linear

equation and int is the point where the straight line

deﬁned by the equation intercepts the Y axis.

Figure 2 depicts the ﬁrst column of the rotation

matrix resulted from PCA application. It says that

the ﬁrst principal component is composed mainly by

the load of the forecast hour registered one day ago.

Table 2 presents the results of the same analysis for

the remaining principal components.

Table 2: Most important variables used for principal com-

ponents characterization.

PC Description

1 Load for the forecast hour, 1 day ago

2 Load for the forecast hour, 5 days ago

3 Load registered 24 hours ago

4 Load for the forecast hour, 1 week ago

5 Load registered 14 hours ago

6 Load registered 11 hours ago

7 Load for the forecast hour, 4 days ago

8 Load for the forecast day and hour,

1 month ago

Based on the rules found and the information de-

tailed on table 2, the following assertions can be

made:

1. the load demand registered in the last twenty-four

hours before the forecast, as well as one day be-

fore and ﬁve days before have an increasing effect

on the load demand

2. the load demand for the same time of the fore-

cast, registered one week ago, decreases the load

demand for the next hour

5.2 Experiment 2

The load demand forecast for the next month is a task

much more difﬁcult than that of the previous experi-

ment. As the window of forecast expands to such a

long time, economic factors begin to play a more im-

portant role in shaping the load demand curve (Srini-

vasan et al., 1999). The load demand for the next

month consists in strategic information to energy sup-

ply companies. It supports the company to purchase

an amount of energy very close to the amount to be

used by its costumers, thus increasing the company’s

proﬁt.

In this experiment, electric demand and climatic

data were used to determine the load demand for the

next month for a small city with a large number of

industries. The data have been stored on a daily ba-

sis, for the period of 2005 to 2007. The ﬁle structure

before PCA is shown below:

• residential load demand registered for 120, 90, 60

and 30 days prior to forecast (4 columns),

• industrial load demand registered for 120, 90, 60

and 30 days prior to forecast (4 columns),

• commercial load demand registered for 120, 90,

60 and 30 days prior to forecast (4 columns)

• average temperature registered for 120, 90, 60 and

30 days prior to forecast (4 columns),

• average relative air humidity registered for 120,

90, 60 and 30 days prior to forecast (4 columns),

• dependent variable: average load demand for the

next 30 days.

The ﬁrst seven principal components were used to

build the training dataset to the neural network. The

reason for the separation of the load in three different

categories relies on the city’s economic structure: it is

mainly industrial. However, the commerce sector has

shown rapid increase in the last decades. Thus, it is

expected that the rules found show high dependency

of industrial load to forecast the average monthly load

for this city.

The neural network selected via tenfold cross-

validation has seven neurons in the input layer, thirty-

two in the hidden layer and one in the output layer.

Shortcut connections were not used. This architec-

ture resulted in a MAPE of 3.26%, however, due to

the elevated quantity of hidden neurons, more than

300 rules were extracted. It means that many fuzzy

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

198

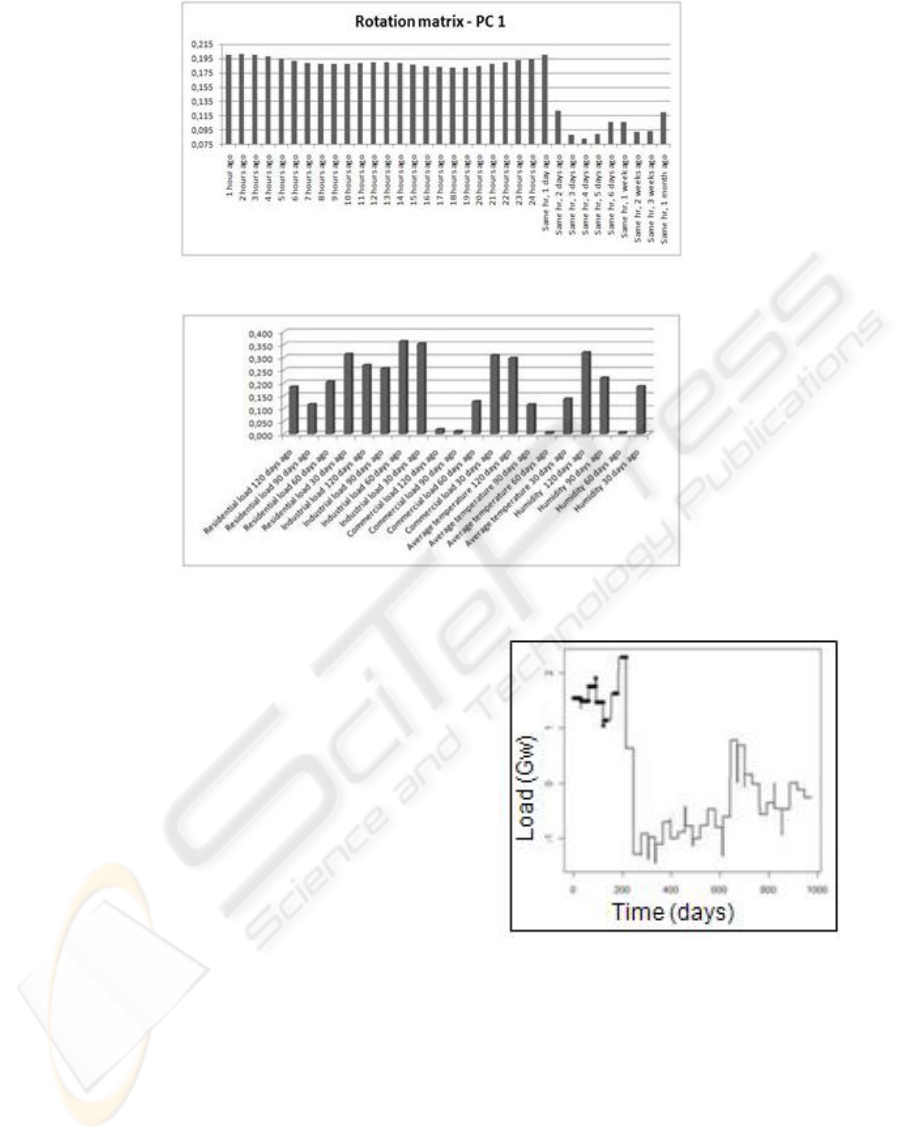
Figure 2: Quantity of information from original dataset used to create the ﬁrst principal component.

Figure 3: Quantity of information from original dataset used to create the ﬁrst principal component.

sets were necessary to map the knowledge acquired

by the network, and these sets refer to very few data

points in the training data. To solve this problem, a

new network structure was used in the rule extrac-

tion procedure: it has eight hidden neurons, and its

MAPE value is of 6.53%. This neural network pro-

duced thirty rules.

Table 3 shows the most important rules extracted

by FAGNIS. They can be read by the same manner as

those shown in the previous experiment. Again, not

all the rules could be presented due to space reasons.

Figure 3 details the data on the ﬁrst column of the ro-

tation matrix resulted from PCA application. It shows

that the industrial load registered sixty days ago has a

strong relation to the load for the next month. How-

ever, it is clear that the industrial load registered thirty

days ago has also a signiﬁcant participation in shap-

ing the overall monthly load. Table 4 presents the

quantity of information given by the original dataset

to build the remaining principal components.

Based on the analysis of the ﬁrst rule found and

the rotation matrix resulted from PCA application

(Table 4), it is possible to verify that the industry load

demand has high impact on the general monthly load

demand of the considered city.

Figure 4 shows the monthly load demand curve

for the city. The dots represent the data points asso-

Figure 4: Monthly load demand and data explained by Rule

ciated with rule number 1. This shows that the Fuzzy

Sets of the ﬁrst rule have elevated energy consump-

tion. The analysis described in this experiment can

be replicated to the other rules, so that all knowledge

learned by the neural network can be acquired.

THE EXTRACTION OF KNOWLEDGE RULES FROM ARTIFICIAL NEURAL NETWORKS APPLIED IN THE

ELECTRIC LOAD DEMAND FORECAST PROBLEM - How Artificial Neural Networks Retain Knowledge and Make

Reliable Forecasts

199

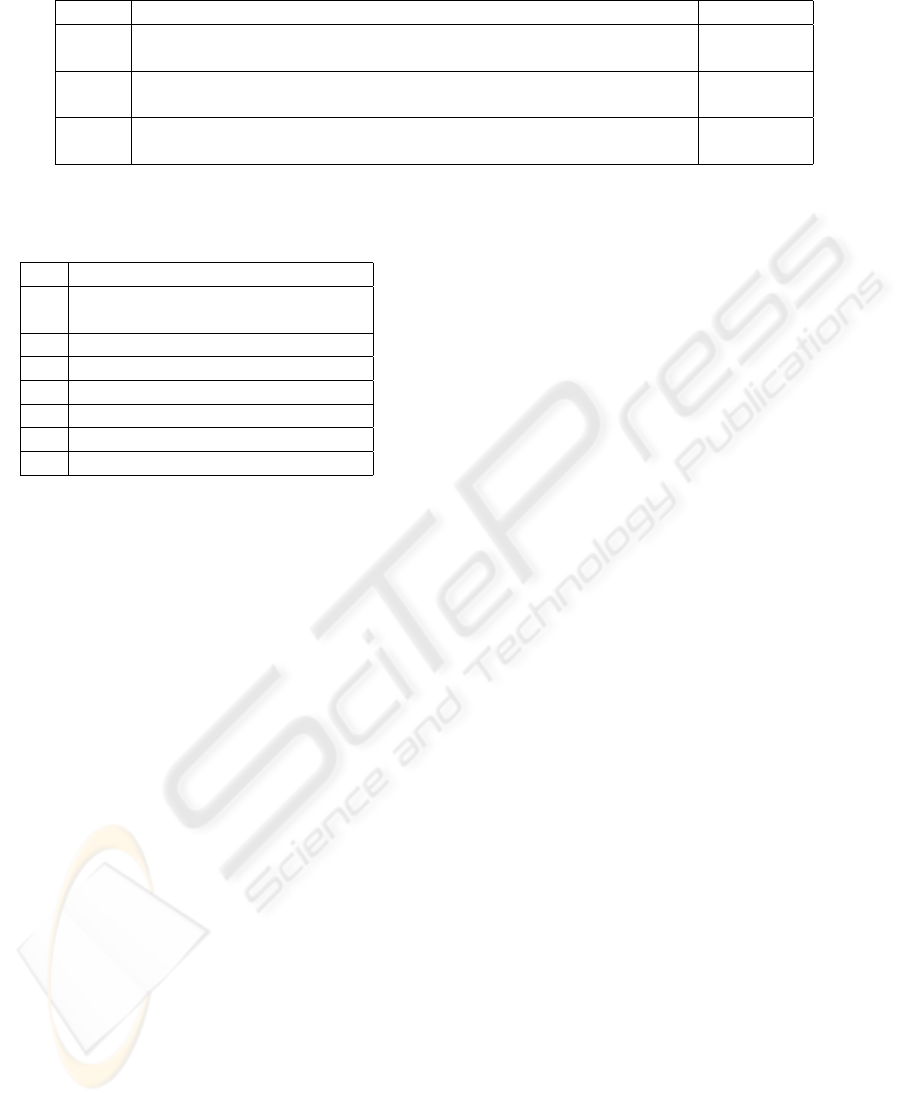
Table 3: Rules found by FAGNIS in experiment 2.

Rule # Rule description Data points

1 IF x = (-2.863 -0.715 1.839 -0.294 0.264 -0.014 0.035) 110

THEN y = (1.442 -0.024 0.001 0.032 -0.033 0.005 -0.004 -0.003)

2 IF x = (2.554 -1.616 -1.161 0.165 0.154 -0.095 -0.022) 68

THEN y = (-0.290 -0.002 -0.378 -0.117 -0.392 0.006 -0.005 -0.235)

3 IF x = (4.356 0.069 2.064 -0.852 -0.152 -0.221 0.596) 42

THEN y = (-2.804 0.874 0.339 -0.386 0.737 -0.027 0.001 0.127)

Table 4: Most important variables used for principal com-

ponents characterization.

PC Description

1 Industrial load, 60 days ago and

Industrial load, 30 days ago

2 Average temperature, 60 days ago

3 Average temperature, 120 days ago

4 Industrial load, 30 days ago

5 Average humidity, 60 days ago

6 Average humidity, 90 days ago

7 Average humidity, 120 days ago

6 CONCLUSIONS

A methodology for the acquisition of rules from neu-

ral networks trained to forecast electric load demand

has been presented here. Results found through sev-

eral experiments (been two of them shown in this

paper) attest the methodology’s efﬁciency in extract

and present high quality rules for different amounts

of time in the future.

Throughout the execution of many experiments, it

was made clear that there is a need to differentiate the

neural networks of load forecast from those used to

rule extraction: the former needs several training cy-

cles in order to obtain a perfect ﬁt to the load demand

curve; the latter requires only a few training cycles to

obtain the overall knowledge about the load demand,

that is, so that a small number of rules can be used to

refer to a large quantity of data points.

Both the forecast model and the rules acquired can

be used as decision support tools for energy supply

companies. For example, several simulations could

be used for the executives to better understand load

demand behavior in different scenarios, such as future

climatic changes.

REFERENCES

Andrews, R., Diederich, J., and Tickle, A. (1995). Survey

and critique of techniques for extracting rules from

trained neural networks. Elsevier Knowledge-Based

Systems.

Angelov, P. (2002). Evolving Rule-based Models: A Tool

for Design of Flexible Adaptive Systems (Studies in

Fuzziness and Soft Computing). Physica-Verlag, Hei-

delberg, ﬁrst edition.

Benitez, J., Castro, J., and Requena, I. (1997). Are artiﬁcial

neural networks black boxes? Neural Networks, IEEE

Transactions on.

Cechin, A. (1998). The Extraction of Fuzzy Rules from Neu-

ral Networks. Shaker Verlag, Tubingen.

Ghods, L. and Kalantar, M. (2008). Methods for long-term

electric load demand forecasting; a comprehensive in-

vestigation. Industrial Technology, 2008. ICIT 2008.

IEEE International Conference on.

Gross, G. and Galiana, F. (1987). Short-term load forecast-

ing. Proceedings of the IEEE.

Hastie, T., Tibshirani, R., and Friedman, J. (2009). The

Elements of Statistical Learning: Data Mining, In-

ference, and Prediction. Springer Series in Statistics,

New York, second edition.

Jang, J., Sun, T., and Mizutani, E. (1997). Neuro-Fuzzy and

Soft Computing. A Computational Approach to Learn-

ing and Machine Intelligence. Prentice-Hall, New Jer-

sey.

Jolliffe, I. (2002). Principal Component Analysis. Springer

Series in Statistics, New York.

Nauck, D., Klawonn, F., and Kruse, R. (1994). Neuronale

Netze und Fuzzy-Systeme. Vieweg and Sohn.

Srinivasan, D., Chang, C., and Liew, A. (1995). Demand

forecasting using fuzzy neural computation, with spe-

cial emphasis on weekend and public holiday forecast-

ing. Power Systems, IEEE Transactions on.

Srinivasan, D., Tan, S. S., Cheng, C., and Chan, E. K.

(1999). Parallel neural network-fuzzy expert system

strategy for short-term load forecasting: system im-

plementation and performance evaluation. Power Sys-

tems, IEEE Transactions on.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

200