
NEURO-FUZZY CONTROL OF NONLINEAR SYSTEMS
Application in a Ball and Beam System
Marconi Cˆamara Rodrigues, F´abio Meneghetti U. Ara´ujo and Andr´e Laurindo Maitelli
Departamento de Engenharia de Computac¸˜ao e Automac¸˜ao
Universidade Federal do Rio Grande do Norte, Natal, RN, Brazil
Keywords:
Control, Hybrid Systems, Fuzzy Systems, Artificial Neural Networks, NEFCON, ANFIS.
Abstract:
This study shows both the development and characteristics of some of the main techniques used to control
nonlinear systems. Starting from a fuzzy controller, it was possible to apply similar learning techniques to
those used in Artificial Neural Networks (ANNs), and evolve to ANFIS and NEFCON neurofuzzy models.
These neurofuzzy models were applied to a real ball and beam plant and both their adaptations and their results
were discussed. For each controller developed the input variables, the parameters used to adapt the variables
and the algorithms applied in each one are specified. The tests were performed in a ball and beam plant and
the results are directed toward obtaining a comparison between the initial and final evolution phase of the
neuro-fuzzy controllers, as well as the applicability of each one according to their intrinsic characteristics.
1 INTRODUCTION
Controllers such as PIDs and those based on the re-
alignment of states, are simple to implement and in-
expensive to operate. However, adjusting their pa-
rameters can take considerable time and their per-
formance is usually limited. A number of automatic
adjustment techniques for PID controller parameters
were developed (Oliveira, 1994; Coelho and Coelho,
1999). These techniques, in addition to raising opera-
tional cost, do not enable PID controllers to resolve
problems, such as controlling nonlinear systems or
maintaining their performance in the presence of un-
certainties or parametric variations.
The need for more encompassing techniques in
the control area led to the emergence of intelligent
techniques such as artificial neural networks, fuzzy
systems, genetic algorithms and other techniques
based on reinforcement learning.
The fuzzy systems and Artificial Neural Networks
(ANNs) are very useful tools for nonlinear systems
control, with or without mathematical models. These
two techniques will be the main focus of this paper,
since it was from their structures that the hybrids pre-
sented here were developed.
ANNs attempt to reproduce the capacity of learn-
ing and generalizing the knowledge of the cerebral
structure of living beings. Based on simple known
structures such as artificial neurons, the data prop-
agate from neuron to neuron via synapses, whose
weights can be adjusted over the course of the learn-
ing process (Haykin, 2001).
Around thirty years after the introduction of the
fuzzy set theory by Lotfi Zadeh (Zadeh, 1965), the
researcher Jyn-Shing Roger Jang published an article
in which fuzzy parameters were calculated using the
backpropagation technique, widely used to adjust the
synaptic weights of ANNs (Jang and S., 1995). This
technique of associating fuzzy with artificial neu-
ral networks became known as neuro-fuzzy and the
model implemented by Jang was called the Adaptive-
Network-Based Fuzzy Inference System, or ANFIS.
Other neuro-fuzzy models were also developed and,
among these, the NEFCON model (neuro-fuzzy con-
troller) stands out for having easy-to-implement char-
acteristics in real time.
This study was developed because of the potential
applicability of ANFIS and NEFCON hybrid intelli-
gent controllers, and showed characteristics of imple-
mentation and of use, the intrinsic characteristics of
each model, as well as a number of advantages and
disadvantages.
This study is divided as follows: section 2, dis-
cusses the neuro-fuzzy implementation approaches
proposed by the ANFIS (Qiang et al., 2008) and NE-
FCON (Shujaec et al., 2002) models. Section 3,
presents the control structure used to obtain the re-
sults of the application, in real time, of the hybrid
201
Câmara Rodrigues M., Meneghetti U. Araújo F. and Laurindo Maitelli A. (2009).
NEURO-FUZZY CONTROL OF NONLINEAR SYSTEMS - Application in a Ball and Beam System.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,
pages 201-206
DOI: 10.5220/0002202502010206
Copyright
c
SciTePress

techniques in a beam and ball plant. The last sec-
tion, 4, contains the conclusions about the techniques
presented and possible future studies.
2 NEURO-FUZZY
CONTROLLERS
Neuro-Fuzzy controllers can aggregate different char-
acteristics of fuzzy controllers and artificial neural
networks in a single structure. Thus, the controller
based on neuro-fuzzy models will have easy-to-
interpret control actions, promoted by the fuzzy con-
trollers, and a learning stage, which is the main char-
acteristic of neural networks. This section presents
two neuro-fuzzy controllers, ANFIS and NEFCON.
2.1 ANFIS Model
The ANFIS model uses a fuzzy controller as its basic
structure, which can be interpreted as a 6-layer neural
network, in which learning techniques such as back-
propagation can be applied (Jang et al., 1997).
To simplify, consider a fuzzy system with two in-
puts (x and y), two membership functions (MFs) for
each input variable and one output z. Figure 1 illus-
trates the structure of the ANFIS model considered.
Layers:0
1
2
1 1
1
z
N
N
N
W
1
W
2
W
3
W
1
W
2
W
3
1
1
3 4
5
X
X
Y
N
W
4
W
4
Y
Figure 1: ANFIS with two inputs (x and y) and one output
(z).
Data flow can be analyzed layer by layer, as shown
below:
• Layer 0: Represents the inputs of the model.
• Layer 1: The neurons of this layer represent the
MFs of the input; that is, the fuzzification phase.
• Layer 2: Represents the number of rules. The
outputs of the previous layer are operated accord-
ing to the inference phase of the fuzzy system con-
sidered. Multiplication is an interesting option,
since it is easy to derive and simple to implement.
• Layer 3: The output of this layer will be the
output of normalized neurons from the previous
layer; that is, the output of each neuron of the pre-
vious layer divided by the sum of the output of all
the neurons in this same layer.
• Layer 4: The function associated to the neurons
of this layer will be the function f(x, y), used by
the Sugeno model, in which x and y are the system
inputs and p, q and r are the adjustable parameters
of the Sugeno function.
• Layer 5: In this layer the sum of the neuron out-
puts of the previous layer occurs, obtaining thus
the control signal for the system.
From the neural network presented, it can be
clearly observed that the neurons that need learning
are present in layers 1 and 4, since layer 1 contains the
input MFs and layer 4 the Sugeno polynomial, which
define the implications of the rules.
The adjustment of controller parameters in the
ANFIS model can be obtained using adaptive tech-
niques such as the backpropagation algorithm. The
derivatives of equations are found in (Jang et al.,
1997). To improve the convergence speed of the al-
gorithm, the η-adaptive technique was used (Rezende
and Maitelli, 1999), in addition to backpropagation.
2.2 NEFCON Model
NEFCON is a neuro-fuzzy controller model based on
the generic architecture of an ANN, but specifically
of a 3-layer perceptron network (figure 2). Making a
parallel between the 3-layer perceptron networks and
the fuzzy systems, we have (Nrnberger et al., 1999):
Layer0
x
y
Layer1
Layer2
f(a,b)=T (a,b)
f(.)=(a,b,c,d)
z
T
Antecedent
Consequent
A1 A2
B1 B2
C1C2C3
Figure 2: NEFCON with 2 inputs (x and y) and 1 output (z).
• Layer 0: This layer represents the inputs. The
MFs are found in the synapses that link this layer
to the following layer and it is in these synapses
that fuzzification occurs.
• Layer 1: This layer (intermediary layer) abstracts
the fuzzy system rules and it is where the actu-
ation level of each output membership function
(MF) is found. In the synapses between this layer
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
202

and the following layer, the actuation level found
acts on the consequent MFs.
• Layer 2: Layer 2 is responsible for defuzzifica-
tion. The algorithm proposed by (Nrnberger et al.,
1999), suggests the use of the mean of the maxi-
mums method for the defuzzification stage, which
reduces the consequent MFs to simple impulses
located in their maximums.
The learning algorithm of the NEFCON model is
based on the idea of reinforcement learning (Sutton
and Barto, 1998). This algorithm can be divided into
two main phases: creating rules and optimizing the
MFs (Rodrigues et al., 2004; Rodrigues et al., 2006).
To create rules the algorithm may or not receive
a set of initial rules. If a set of initial rules is re-
ceived, then the rule creation phase will optimize it.
It is necessary to specify both the actuation intervals
for each input and the actuation interval for the out-
put, since these intervals enable the interval to com-
pare different-sized inputs and create a rule to reduce
the input of greatest error.
To illustrate this idea, consider the actuation inter-
vals of two inputs (E1 and E2) are [5, 5] and [-0.5,
0.5], respectively. The input E1 error is 1, and the E2
error is 0.3. To calculate the error of an input in terms
of its actuation interval, the value of the input error is
divided by the size of the actuation interval. Thus, the
error of E1 will be 0.1, whereas the error of E2 will be
0.3. Observe that even though it has a smaller abso-
lute value, the value of input E2 is greater than that of
input E1, a situation that leads the algorithm to create
a rule with a tendency to minimize the error of input
E2. Thus, the algorithm will discover which rule from
the set of rules is activated with greatest strength and
greatest µ. This rule will activate an output MF that
will be obtained by comparing the input in its actua-
tion interval and the output interval divided into out-
put MFs.
Different from that suggested by the algorithm
that inspired this work (Nrnberger et al., 1999), a pre-
viously created rule can be modified at any moment if
a different rule is found for the situation. There is also
no need to modify the structure of the MFs, given that
they will be treated in a later phase.
To optimize the MFs, the algorithm uses a strategy
similar to that used by reinforcement learning. When
an input MF is activated, it contributes to reducing or
increasing the error. If the action produced provokes
an increase in system error, this MF has its actuation
field reduced. Otherwise, the MF has its actuation in-
terval increased. A similar situation occurs with the
output MFs. However, with these, the gain or loss
occurs in their intensity; that is, the MF that collab-
orates with the increased error will have its intensity
reduced; otherwise, the intensity will be increased.
Mathematically, we have that the plant E error
is found according to the insertion of inputs into the
plant. The contribution, tr, of each rule for the output
is estimated and error Er is calculated for each rule
unit, according to the following equation,
Er = µ · E · sgn(tr) (1)
in which:
sgn(tr) = tr signal
With these data, the consequent modifications can
be represented by:
∆b
i
= η· µ · E (2)
And the antecedent modifications by:
∆a
(i)
j
= −η· Er · (b
(i)
j
− a
(i)
j
) (3)
∆c
(i)
j
= η· Er· (c
(i)
j
− b
(i)
j
) (4)
in which:
η = Learning coefficient
a, b, c = Vertices of the membership functions
It can be easily observed that the algorithm does
not alter the position of the MF of the antecedents. Its
base is only increased or decreased proportionally on
both sides; that is, if the MF has a positive contribu-
tion, there will be greater likelihood of its occurring
again.
A number of restrictions were inserted to avoid
the overlapping of more than two MFs and to avoid
the emergence of gaps between them. Therefore, an
overlap between zero and 50% must be guaranteed;
that is, the vertices of a triangle must be contained in
the interval corresponding to the middle of the base of
neighboring triangles.
3 APPLICATION IN THE BALL
AND BEAM SYSTEM
The ball and beam system, in which the controllers
were tested, is composed basically of a beam-ball sys-
tem, a servo motor with a reducer gearbox and a ruler
with a ball of reference. There are three sensors, one
to measure the position of the reference ball, another
for the position of the ball to be controlled and one to
measure the angular position of the servo motor (fig-
ure 3).
The aim of the controller is to makethe ball placed
on the beam to follow the pathway specified by the
reference ball. Thus, a control system is designed to
NEURO-FUZZY CONTROL OF NONLINEAR SYSTEMS - Application in a Ball and Beam System
203
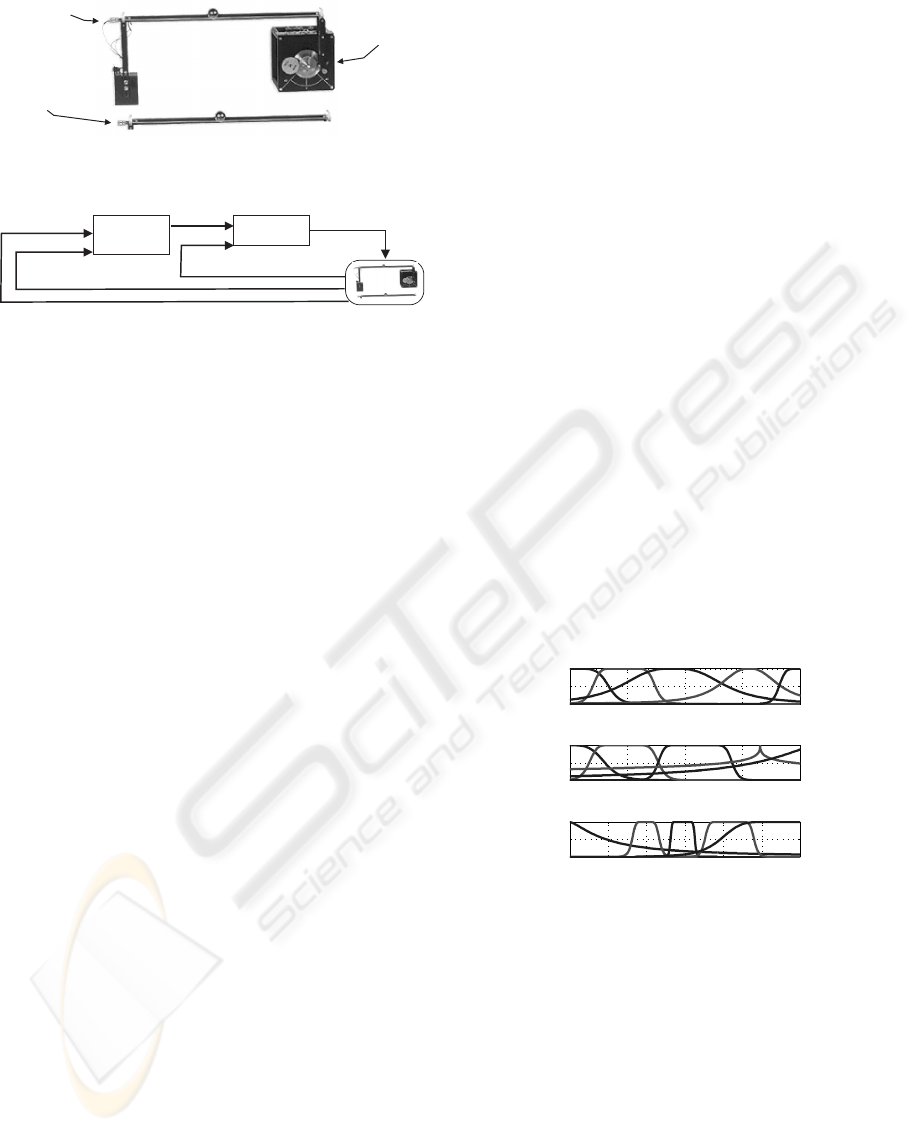
Referenceball
sensor
Controlledball
sensor
Servomotor
sensor
Figure 3: Sensor location in the ball and beam system.
Ball-Beam
Intelligent
Controller
PID
Ball
Reference
Ref Ang
Angle
Motor Tension
Figure 4: Flowchart illustrating the ball and beam control
loops.
send a voltage to the servo motor, which, upon mov-
ing, raises or lowers one of the ends of the beam, caus-
ing the ball to move.
The control system designed for the ball and beam
is divided into two loops (figure 4): one external,
where an intelligent controller is responsible for re-
ceiving the position of the ball to be controlled and
the position of the reference ball and from this, pro-
vide the reference angle for the second loop, where a
PID controller generates a control signal, which is re-
quired for the servo motor to position itself according
to the reference angle supplied by the first controller.
The use of the intelligent controller to substitute
the two control loops of the plant is a considerable
challenge. Thus, it was decided to use hybrid tech-
niques to substitute only the external loop, given that
the internal loop functions sufficiently well with the
PID designed and the external loop is a sufficient chal-
lenge for the proposal.
3.1 Results with ANFIS
The ANFIS model will be optimized by backpropaga-
tion. To achieve this, training pairs (points) must be
obtained. A PID (Proportional Integrative Derivative)
controller was used to obtain the training pairs, substi-
tuting the intelligent controller (figure 4). The choice
of three inputs for the ANFIS model was based on the
characteristics of the controller to be copied, namely
the PID. The three inputs considered were the errors:
current and previous of the ball to be controlled with
respect to the reference ball, and the previous refer-
ence angle.
The training point capture stage was followed by
the training stage of the ANFIS model. The training
algorithm used the input-output pairs obtained with
the PID controller to adapt the adjustable parameters
of the system.
Seen as a fuzzy system, it has 5 bell-shaped MFs
for each input variable. Thus, the intersections be-
tween the MFs form 125 possible rules that reference
first-order polynomials (px+ qy + rz+ s), as a func-
tion of input variables x = current error, y = previous
error and z = previous reference angle. The variables
p, q, r and s are the adjustable parameters of the poly-
nomials and all were initiated with a value of 0 (zero).
The learning coefficient for this system was ini-
tiated with η = 10
−6
, the initial values for the MFs
were uniformly distributed within the intervals and
the sample period considered was 0.05 s.
The initial value for variable η and the intervals in
which the MFs were distributed were two of the great-
est difficulties in implementing the model. When the
η value was elevated (around 10
−4
for this model) or
when the intervals were very different from the real-
ity of the system to be controlled, the programbecame
unstable.
An association with the fuzzy system shows that
the equivalent neural network will have the following
number of neurons in each layer: 3 - layer 0; 15 -
layer 1; 125 -layers 2, 3 and 4; 1 - layer 5.
For training, a total of 800 points were collected
from the PID of the external loop of the control sys-
tem that acts on the ball and beam. After training, the
input MFs have optimized shapes, as shown in fig. 5.
−10 −5 0 5 10
0
0.5
1
Fuzzy error
−10 −5 0 5 10
0
0.5
1
Previous fuzzy error
−6 −4 −2 0 2 4 6
0
0.5
1
Previous reference angle
Figure 5: Membership functions after ANFIS adjust.
For an effective learning validation, the controller
trained in the ball and beam plant was used for a se-
quence of preestablished reference points, which dis-
pensed with the use of the reference beam. The ef-
fect of the controller on the plant can be observed
in figure 6. First, the reference received a pseudo
ramdom signal (figure 6). Notice that in the signal
changes, the reference is not followed with much per-
fection by the neuro-fuzzy controller. Analysis of the
control signal from ANFIS showed that the beam re-
ceives the angle which, in theory, would take the ball
to the position of reference. However, the influence of
dry attrition causes the ball to be controlled to remain
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
204

0 10 20 30 40 50 60 70
0
10
20
30
40
Time (s)
Position on the beam (cm)
Figure 6: Neuro-fuzzy controller of the ANFIS model
(dashed), reference (solid) and PID (dashdot).
immobile. The PID controller has a control signal
with many more oscillations than does ANFIS and,
thus, manages to avoid interference from dry attrition.
When the reference received a sine signal, the neuro-
fuzzy controller follows the reference as well as the
PID controller and sometimes more accurately. How-
ever, at low velocities (extremes above and below the
graphs), accuracy is reduced by dry attrition.
3.2 Results with NEFCON
For this model two inputs with five triangular func-
tions each were used, and one output, the angle of
reference, with seven singleton-type MFs. The input
MFs are initiated with 50% overlap and symmetri-
cally divided within their actuation interval, which is
supplied by the designer. The maximum number of
active rules for the system is 25. The learning con-
stant for the controller was considered to be 10
−3
and
the sampling period for this model was 0.02 seconds.
This value is due to the fact that the NEFCON model
has a lower computational cost than that of the ANFIS
model.
The position error of the ball and its variation were
defined as system inputs. The value desired for both
inputs was defined as zero and the execution range
used for these variables was between -20 and 20 cm
for the error and between -0.6 and 0.6 cm/s for the er-
ror variation. With respect to the output variable, the
reference angle can vary from -45 to 45 degrees. The
initial rule base was considered empty, except for the
central rule, which received the output value equiva-
lent to the zero reference angle.
As previously mentioned, NEFCON has its learn-
ing phase in real time. To show the development of
this learning while the algorithm attempts to control
the plant, a sine wave in the reference beam was used
as a learning sequence. The rule creation phase was
the first to enter into operation and its result is pre-
sented in table 1, where NH = Negative high, NL =
Negative low, ZE = Zero, PL = Positive low, PH =
Positive high, NE = Negative and PO = Positive.
Table 1: Rules found after 35 seconds of rule creation.
Error variation
NH NL ZE PL PH
E NH - - - - -
R NL NH - NE PO PH
R ZE NH NL ZE PL -
O PL NH NL PL PH PH
R PH - - - - -
−20 −10 0 10 20
0
0.5
1
1.5
Fuzzy error
−0.4 −0.2 0 0.2 0.4 0.6
0
0.5
1
1.5
Fuzzy error variation
−50 0 50
0
0.5
1
1.5
Fuzzy outputs
Figure 7: Membership functions after NEFCON adjust.
The second part of the algorithm functions as a
fine adjustment of the fuzzy parameters by only mov-
ing the MFs while searching for an optimal adjust-
ment. The MFs have the shape illustrated in fig. 7.
Observe that a situation of non symmetry occurred
in the central MF (corresponding to membership ZE)
of the second input (Error variation) of the neuro-
fuzzy controller. Even though the algorithm tends to
adjust the two sides symmetrically, the restrictions to
gap formation between the MFs enable this asymmet-
ric condition. We can observe also the compensation
supplied by the algorithm for the output MF to cali-
brate the zero angle of the plant.
The result obtained with the reference sequence is
shown in figure 8.
A numerical comparison between the results ob-
tained for this second reference sequence is presented
in table 2.
This table, despite showing the superiority of the
0 10 20 30 40 50 60 70
0
10
20
30
40
Time (s)
Position on the beam (cm)
Figure 8: Neuro-fuzzy controller of the NEFCON model
(dashed) and reference (solid).
NEURO-FUZZY CONTROL OF NONLINEAR SYSTEMS - Application in a Ball and Beam System
205

Table 2: Numerical comparison between the controllers.
METHOD NEFCON ANFIS PID
IAE 2.13 5.55 5.29
ISE 10.82 49.12 41.94
controller that used the NEFCON model, does not
serve as a comparison parameter,since ANFIS copied
the PID and NEFCON is optimal by its own structure.
4 CONCLUSIONS
This study showed how to implement and apply two
neuro-fuzzy techniques to generate controllers (AN-
FIS and NEFCON). A number of applications were
developed and discussed in such a way that both tech-
niques could be applied successfully.
The controller based on the ANFIS model was de-
veloped with learning based on the backpropagation
algorithm, using training pairs extracted from a PID
controller and, in addition to controlling the ball and
beam system, eliminated the high control signal vari-
ations in the learning stage. This fact makes ANFIS
more susceptible to the effects of dry attrition present
in the system. The controller based on the NEFCON
model used a learning technique based on reinforce-
ment learning with a number of alterations, and also
achieved satisfactory results, since it successfully im-
plemented the task of controlling the ball and beam
system.
When compared to ANFIS, NEFCON is less com-
plex to use, requiring it only to inform the algorithm
on the admissible intervals for the input and output
variables of the controller. This greater facility en-
ables learning that is more directed toward user needs.
Optimization techniques such as genetic algo-
rithms and ant colonies, among others, are some other
techniques that may promote an even greater im-
provement in the hybrid models and might include
future characteristics such as the mutation or evolu-
tion of the various forms associated to the structures.
Another factor that could be analyzed is the compati-
bility of the models developed, in order to apply both
in a same plant, in such a way that these models would
collaborate or agree with each other.
ACKNOWLEDGEMENTS
The authors would like to thank CAPES-Brasil and
CENPES-Petrobras for the financial support.
REFERENCES
Coelho, L. S. and Coelho, A. A. R. (1999). Algoritmos evo-
lutivos em identificao e controle de processos: uma
viso integrada e perspectivas. SBA Controle & Au-
tomao, 10(1):13–30.
Haykin, S. (2001). Redes Neurais Artificiais: Princpios e
prtica. Bookman, 2 edition.
Jang, J. R. and S., C.-T. (1995). Neuro-fuzzy modeling and
control. Proceedings of the IEEE, 83(3):378–406.
Jang, J.-S. R., Sun, C.-T., and Mizutani, E. (1997). Neuro-
Fuzzy and Soft Computing, A Computational Ap-
proach to Learn and Machine Intelligence. Prentice-
Hall, 1 edition.
Nrnberger, A., Nauck, D., and Kruse, R. (1999). Neuro-
fuzzy control based on the nefcon-model: Recent de-
velopments. Soft Computing 2, pages 168–182.
Oliveira, J. P. B. M. (1994). Review of auto-tuning tech-
niques for industrial pi controllers. Master’s thesis,
University of Salford.
Qiang, S., Zhou, Q., Gao, X. Z., and Yu, S. (2008). Anfis
controller for double inverted pendulum. The IEEE
International Conference on Industrial Informatics,
pages 475–480.
Rezende, J. A. D. and Maitelli, A. L. (1999). Um esquema
de neurocontrole com treinamento em tempo real apli-
cado ao posicionamento de um servomotor. Simpsio
Brasileiro de Automao Inteligente.
Rodrigues, M. C., de Arajo, F. M. U., and Maitelli, A. L.
(2006). Controladores neuro-fuzzy para sistemas no-
lineares. Congresso Brasileiro de Automtica.
Rodrigues, M. C., Maitelli, A. L., and de Arajo, F. M. U.
(2004). Controle neuro-fuzzy com treinamento em
tempo real aplicado a um sistema ball and beam. Con-
gresso Brasileiro de Automtica.
Shujaec, K., Sarathy, S., Nicholson, R., and George, R.
(2002). Neuro-fuzzy controller and convention con-
troller: a comparison. World Automation Congress,
13:207–213.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement Learn-
ing, An Introduction. Bradford Book, 1 edition.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control,
8:338–353.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
206
