Systematic Formulation and Computation of Subjective

Spatiotemporal Knowledge Based on Mental Image

Directed Semantic Theory: Toward a Formal

System for Natural Intelligence

Masao Yokota

Department of System Management, Faculty of Information Engineering

Fukuoka Institute of Technology

3-30-1, Wajiro-higashi, Higashi-ku, Fukuoka-shi, 811-0295, Japan

Abstract. The author has been challenging to model natural intelligence as a

formal system based on his original semantic theory “Mental Image Directed

Semantic Theory (MIDST)”. As the first step for this purpose, this paper

presents a brief sketch of the attempt on systematic representation and compu-

tation of subjective spatiotemporal knowledge in natural language based on cer-

tain hypotheses of mental image in human.

1 Introduction

The author and his co-workers have been studying integrated multimedia understand-

ing for intuitive human-robot interaction, that is, interaction between non-expert or

ordinary people and home robots [1, 2]. In such a situation, natural language is the

leading information medium for their communication as well as for the communica-

tion between ordinary people because it can convey the exact intention of the sender

to the receiver due to its syntax and semantics common to its users, which is not nec-

essarily the case for another medium such as gesture or so. For such an intuitive hu-

man-robot interaction intended here, it is essential to develop a systematically com-

putable knowledge representation language (KRL) as well as representation-free

technologies such as neural networks for processing unstructured sensory/motory data.

This type of language is indispensable to knowledge-based processing such as under-

standing sensory events, planning appropriate actions and knowledgeable communi-

cation with ordinary people in natural language, and therefore it needs to have at least

a good capability of representing spatiotemporal events that correspond to hu-

man/robotic sensations and actions in the real world. Most of conventional methods

have provided robotic systems with such quasi-natural language expressions as

‘move(Velocity, Distance, Direction)’, ‘find(Object, Shape, Color)’ and so on for

human instruction or suggestion, uniquely related to computer programs to deploy

sensors/ motors [3, 4]. These expression schemas, however, cannot provide a firm

bridge between natural language and programs [5], and what is worse is that they are

Yokota M. (2009).

Systematic Formulation and Computation of Subjective Spatiotemporal Knowledge Based on Mental Image Directed Semantic Theory: Toward a Formal

System for Natural Intelligence.

In Proceedings of the 6th International Workshop on Natural Language Processing and Cognitive Science , pages 133-142

DOI: 10.5220/0002203701330142

 SciTePress

too linguistic or coarse to represent and compute sensory/motory events in such an

integrated way as intended here.

In order to solve this problem, the author has employed the formal language so

called ‘Language for Mental-image Description (L

)’ proposed in his original se-

mantic theory ‘Mental Image Directed Semantic Theory (MIDST)’ [1, 2]. The key

idea of MIDST is the model of human attention-guided (i.e. active) perception yield-

ing omnisensory images that inevitably reflect certain movements of the focus of

attention of the observer (FAO) scanning certain matters in the world, either inside or

outside of the mind. More analytically, these omnisensory images are associated with

spatiotemporal changes (or constancies) in certain attributes of the matters scanned by

FAO and modeled as temporally parameterized “loci in attribute spaces”, so called, to

be formulated in the formal language L

. This language has already been imple-

mented on several types of computerized intelligent systems including IMAGES-M

[1, 2]. The most remarkable feature of L

is its capability of formalizing spatiotem-

poral matter concepts grounded in human/robotic sensation while the other similar

KRLs are designed to describe the logical relations among conceptual primitives

represented by lexical tokens [6, 7] with the risk of “predicate drift” [8]. The final

goal of this study is to build a formal system for natural intelligence so as to facilitate

intuitive but coherent interaction between ordinary people and robots. A formal sys-

tem is defined as a pair of a formal language and a deductive system consisting of the

axioms and inference rules employed for theorem derivation. L

is a formal lan-

guage for many-sorted predicate logic with 5 types of terms specific to the mental

image model. Therefore, the deductive system intended here is to be based on the

deductive apparatus for predicate logic.

The remainder of this paper is organized as follows. Section 2 introduces the for-

mal system intended here, presenting a number of postulates of human subjective

knowledge pieces about space and time. Conclusions and planned future work are

given in the final section.

2 Formal System for Natural Intelligence

The symbols of L

for the deductive system are listed as (i)-(ix) below. These sym-

bols are possibly subscripted just like A

, G

, etc.

(i) logical connectives: ~, ∧, ∨, ⊃, ≡

(ii) quantifiers : ∀, ∃

(iii) auxiliary constants : ., (, )

(iv) sentence variables : χ

(v) predicate variables : ψ

(vi) individual variables

a) matter variables : x, y, z

b) attribute variables : a

c) value variables : p, q, r, s, t

d) pattern variables : g

e) standard variables : k

(vii) sentence constants : N

134

(viii) predicate constants : L, =, ≠, >, < (and others to be introduced where needed)

(ix) individual constants

a) matter constants : to be introduced where needed

b) attribute constants : A, B

c) value constants : to be introduced where needed

d) pattern constants : G

e) standard constants : K

(x) function constants: arithmetic operators such as +, -, etc. (and others to be intro-

duced where needed)

(xi) meta-symbols: ⇔, →, ↔ (and others to be introduced where needed)

(xii) others: to be defined by the symbols above.

The system is a many-sorted predicate logic with five kinds of individuals em-

ployed for one special predicate constant ‘L’ so called ‘Atomic Locus’. Except this

point, the syntactic rules and the theses of the system are the same as those of the

conventional predicate logic. The predicate ‘L’ is such a seven-place predicate as is

given by expression (1).

L(ω

, ω

)

(1)

Expression (1) is a well-formed formula (i.e. wff) called ‘Atomic locus formula’ if

and only if the conditions below are satisfied. A well-formed formula consisting of

atomic formulas and logical connectives is called simply ‘Locus formula’.

(a)

is a matter term (variable or constant)

(b)

is a matter term

(c)

is a value or a matter term

(d)

is a value or a matter term

(e)

is an attribute term

(f)

is a pattern term

(g)

is a standard (or matter) term

The intuitive interpretation of (1) is given as follows.

“Matter ω

causes Attribute ω

of Matter ω

to keep (ω

= ω

) or change (ω

≠

) its values temporally (ω

=Gt) or spatially (ω

=Gs) over a certain absolute

time-interval, where the values ω

and ω

are relative to the standard ω

.”

Here, Matter terms at Values or Standard represent their values in each place at the

time or over the time-interval. When

, the locus indicates monotonic change (or

constancy) of the attribute in time domain, and when

, that in space domain.

The former is called ‘temporal event’ and the latter, ‘spatial event’. For example, the

motion of the ‘bus’ represented by S1 is a temporal event and the ranging or exten-

sion of the ‘road’ by S2 is a spatial event whose meanings or concepts are formulated

as (2) and (3), respectively, where ‘A

’ denotes the attribute ‘Physical Location’.

These two formulas are different only at the term ‘Pattern’.

(S1) The bus runs from Tokyo to Osaka.

(S2) The road runs from Tokyo to Osaka.

135

(∃x,y,k)L(x,y,Tokyo,Osaka,A

,k)∧bus(y)

(2)

(∃x,y,k)L(x,y,Tokyo,Osaka,A

,k)∧road(y) (3)

It has been often argued that human active sensing processes may affect perception

and in turn conceptualization and recognition of the physical world while such cogni-

tive processes or products have seldom been formulated for computation [9-12]. The

author has hypothesized that the difference between temporal and spatial event con-

cepts can be attributed to the relationship between the Attribute Carrier (AC) (i.e. the

matters at

) and the Focus of the Attention of the Observer (FAO). To be brief, it is

hypothesized that FAO is fixed on the whole AC in a temporal event but runs about

on the AC in a spatial event. Consequently, the bus and FAO move together in the

case of S1 while FAO solely moves along the road in the case of S2. That is, all loci

in attribute spaces are assumed to correspond one to one with movements or, more

generally, temporal events of FAO. The duration of a locus corresponds to an abso-

lute time-interval over which FAO is put on the corresponding phenomenon outside

or inside the mind. Such an absolute time-interval is suppressed in an atomic locus

formula because it is assumed that people cannot measure the absolute time by any

chronograph but a certain relative time (Actually, people do not always consult a

chronograph even if they can). MIDST has employed ‘tempo-logical connectives

(TLCs)’, to be introduced later, denoting both logical and temporal relations between

loci by themselves because these must be considered simultaneously in locus articula-

tion. The attribute spaces for humans correspond to the sensory receptive fields in

their brains. At present, about 50 attributes (i.e. Attribute Constants) have been ex-

tracted exclusively from Japanese and English words [13]. Correspondingly, 6 cate-

gories of standards (i.e. Standard Constants) [1, 2] have been extracted after the con-

ventional categorization [9] assumed necessary for representing values of each

attribute. In general, the attribute values represented by words are relative to certain

standards. These standards are to be utilized exclusively for coping with vagueness

and controlling granularity of attribute values.

The deductive system employs ‘tempo-logical connectives (TLCs)’ with which to

represent both temporal and logical relations between two loci over certain time-

intervals. Therefore, TLCs are for interval-based time theories with relative temporal

relations but are generalized for all the binary logical connectives (i.e. conjunction

‘∧’, disjunction ‘∨’, implication ‘⊃’ and equivalence ‘≡’) unlike the conventional

ones exclusively for the conjunction [14, 15]. The definition of a tempo-logical con-

nective C

is given by D1, where

and C refer to one of pure temporal relations

indexed by an integer ‘i’, a locus, and an ordinary binary logical connective such as

the conjunction ‘∧’, respectively. The definition of each τ

discriminates 13 types of

temporal relations by the integer suffix ‘i’ ranging from –6 to 6, respectively corres-

ponding to ‘overlapped-by’

, ‘after’, ‘finished-by’, ‘contains’, ‘started-by’, ‘met-by’,

‘equals’, ‘meets’, ‘starts’, ‘during’, ‘finishes’ ‘before’, and ‘overlaps’. This is in

accordance with the conventional notation [15] which, to be strict, is for ‘temporal

conjunctions (=∧

)’ but not for pure ‘temporal relations (=

)’. The TLCs used most

frequently are ‘SAND (∧

)’ and ‘CAND (∧

)’, standing for ‘Simultaneous AND’ and

‘Consecutive AND’ and conventionally symbolized as ‘Π’ and ‘•’, respectively.

136

D1.

⇔ (χ

C χ

) ∧ τ

(χ

, χ

)

where τ

-i

(χ

, χ

) ≡ τ

(χ

, χ

) (∀i∈{0,±1,±2,±3,±4,±5, ±6})

In order for explicit indication of absolute time elapsing, ‘Empty Event’ denoted

by ‘ε’ is introduced as D2 with the attribute ‘Time Point (A

)’ and the Standard of

absolute time ‘K

’, where R and

denote the total sets of real numbers and absolute

time intervals, respectively. (Usually people can know only a certain relative time

point by a clock that is seldom exact and that is to be denoted by another Standard in

the L

.) According to this scheme, the suppressed absolute time-interval [t

, t

] of a

locus χ can be indicated as (4).

D2.

ε([t

])⇔(∃x,y,g)L(x,y, t

,g,K

)

where [t

]∈

={[t

, t

] | t

, t

∈R)}

χΠε([t

]) (4)

People can transform their mental images in several ways such as mental rotation

[16]. Here are introduced and defined two kinds of such mental operations, namely,

‘reversal’ and ‘duplication’. For example, people can easily imagine the reversal of an

event just like ‘rise’ versus ‘sink’. This mental operation is here denoted as ‘R’ and

recursively defined as D3, where χ

stands for a locus. The reversed values p

and q

depend on the properties of the attribute values p and q. For example, p

=p, q

=q for

; p

=-p, q

=-q for A

D3.

(χ

•χ

)

⇔χ

•χ

(χ

Πχ

)

⇔ χ

Πχ

(x,y,p,q,a,g,k) ⇔ L(x,y,q

,a,g,k)

For another example, people can easily imagine the duplication or repetition of an

event just like ‘visit twice’ versus ‘visit once’. This operation is also recursively de-

fined as D4, where ‘n’ is an integer representing the frequency of a locus formula χ.

D4.

⇔ χ

(n=1)

⇔ χ•χ

n-1

(n>1)

An event here, usually referred by a verb, preposition, adjective or so in natural

language, is defined as a spatiotemporal relation among certain matters in the world,

which is to be conceptualized as a generalization of a perceptual locus, namely, a

combination of atomic loci articulated by tempological conjunctions (i.e. ∧

) with the

abstraction operator ‘λ’. For example, the English verb concepts ‘carry (=convey)’

and ‘shuttle’ are to be defined as (5) and (6), respectively. These can be depicted as

Fig.1-a and b, respectively. In turn, the expression (7) is the definition of the English

verb concept ‘fetch’ depicted as Fig.1-c. This implies such a temporal event that ‘x’

goes for ‘y’ and then comes back with it. In the same way, the English verb concept

‘hand’ or ‘receive’ depicted as Fig.1-d is defined equivalently as (8) or its abbrevia-

137

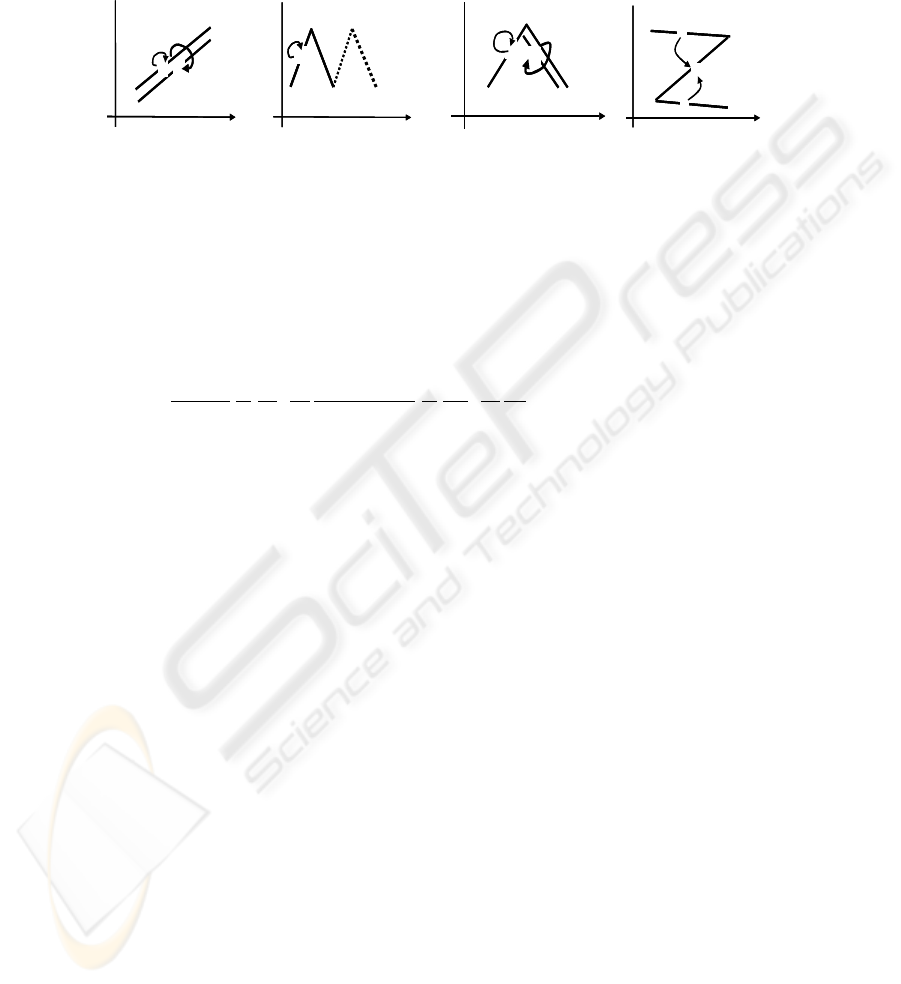
tion (9) where Event Causers (i.e. the matters at ω

) are merged into a set. Such locus

formulas as correspond with natural event concepts are called ‘Event Patterns’ and

about 40 kinds have been found concerning the attribute ‘Physical Location (A

)’

[1,2].

A12

Time

A12

Time

A12

Time

A12

Time

A12

Time

A12

Time

A12

Time

A12

Time

A12

Time

(a) (b) (c) (d)

Fig.1. Pictorial interpretation of (a) ‘carry’, (b) ‘shuttle’, (c) ‘fetch’ and (d) ‘hand/receive’.

(λx,y)carry(x,y)⇔(λx,y)convey(x,y)⇔(λx,y)(∃p,q,k)L(x,x,p,q,A

,k)Π

L(x,y,p,q,A

,k)∧x≠y∧p≠q

(5)

(λx)shuttle(x)⇔(λx)(∃p,q,k)(L(x,x,p,q,A

,k)•L

(x,x,p,q,A

,k))

∧p≠q

∧n≥1⇔(λx)(∃p,q,k)(L(x,x,p,q,A

,k)•L(x,x,q,p,A

,k))

∧p≠q∧n≥1

(6)

(λx,y)fetch(x,y)⇔(λx,y)(∃p

,k)L(x,x,p

, A

,k)

•((L(x,x,p

,k) ΠL(x,y,p

, A

,k)) ∧x≠y∧p

≠p

(7)

(λx,y,z)hand(x,y,z)⇔(λx,y,z)receive(z,y,x)

⇔(λx,y,z)(∃k)L(x,y,x,z,A

,k)ΠL(z,y,x,z,A

,k)∧x≠y∧y≠z∧z≠x

(8)

⇔(λx,y,z)(∃k)L({x,z},y,x,z,A

,k)∧x≠y∧y≠z∧z≠x

(9)

Employing TLCs, tempo-logical relationships between miscellaneous event con-

cepts can be formulated without explicit indication of time intervals. For example, an

event ‘fetch(x,y)’ is necessarily finished by an event ‘carry(x,y)’ as indicated by the

underline at (7). This fact can be formulated as (10), where ‘⊃

-4

’ is the ‘implication

(⊃)’ furnished with the temporal relation ‘finished-by (τ

-4

)’. This kind of formula is

not an axiom but a theorem deducible from the definitions of event concepts in the

deductive system intended here.

(∀x,y) fetch(x,y) ⊃

-4

carry(x,y)

(10)

A matter, usually referred to by a noun in natural language, is to be conceptualized

as a conjunction of the mental images of itself and its relations with others that in turn

are to be reduced to certain loci in attribute spaces. In the formal system, a matter

concept ‘ψ’ is introduced in such a context as (11), where ‘ψ

’ and ‘ψ

’ are to

represent the conceptual images of itself and its relations with others, respectively,

and in turn to be reduced to atomic locus formulas of all the attributes.

(λz)ψ(z)⇔(λz)ψ

(z)∧ψ

(z)

(11)

138

Whereas ψ(z) must be a total description of all the attributes, for simplicity here is

to be given only its important part with the symbol ‘%’ representing its abbreviated

part. The part ψ

(z) is given as a combination of atomic locus formulas for the

Attribute Carrier ‘z’ without any other specific matter involved unlike the other part

(z). For example, the matter called ‘ice’ can be conceptualized as (12). This reads

that ice is always 0°C cold or less, is always of no vitality and melts into water (or is

something from that H

O) changes into water)’. In turn, the matter ‘snow’ can be

conceptualized as (13), reading ‘Snow is powdered ice attracted from the sky by the

earth’. ‘A

’, ‘A

’ and ‘A

’ refer to ‘Temperature’, ‘Vitality’ and ‘Quality’, respec-

tively. The special symbol ‘_’, defined by (14), is a variable bound by an existential

quantifier but does not refer to any specific matter or so in the context while ‘*’ and

‘φ’ represent ‘always’ and ‘no value (or matter)’, respectively, defined by (15) and

(16).

(λx)ice(y)⇔(λx)ice

(z)∧ice

(x)

(λx)ice

(x)⇔(λx)((∃p,q)L(_,x,p,q,A

,_)

∧p≤0°C∧q≤0°C)*∧L*(φ,x,φ,φ,A

,φ)∧%

(λx)ice

(x)⇔(∃z,x

)L(_,z,x,x

,_)∧water(x

)

(∧H

O(z))∧%

(12)

(λx)snow(x)⇔(λx)(∃x

)((L(_,x,x

,_)

∏L(Earth,x,Sky,Earth,A

,_)) ∧powder(x

)∧ice(x

)∧% (13)

L(…,ω

,_,ω

,…)⇔(∃ω)L(…,ω

,ω,ω

,…) (14)

χ*⇔(∀[p,q]) χ Π ε([p,q]) (15)

L(…,ω

,φ,ω

,…)⇔~(∃p)L(…,ω

,p,ω

,…) (16)

All knowledge pieces resulted from an individual's everyday experience are inevit-

ably subjective (to him/her), that is, not necessarily intelligible to others. In this sense,

the formal system is subjective (to the author) as far as it employs (domain-specific)

constants other than logical ones such as logical connectives (generally assumed to be

objective). This section focuses on subjective or empirical laws, so called “post-

ulates”, of space and time in order for spatiotemporal language understanding. These

postulates are to be treated as equivalents to axioms.

The postulates P1 and P2 state that a matter never has different values of an

attribute with a standard at a time. These are called “Postulates of Identity in As-

signed Values”. P1 is employed exclusively to detect semantic anomaly in such a

sentence as “The red box is black” while P2 is useful to detect event gaps in such a

context as “Tom was in London yesterday and he is in Paris today.”

The syntax of L

allows Matter terms to appear at Values and Standard in order to

represent their values in each place at the time and over the time-interval, respectively.

This rule can be formulated as P3 and P4. The postulate P3 is to be utilized for such

inference as “Mary went to Tom when he was in the garden. Therefore, Mary went to

the (same) garden.” while P4 is for such inference as “Jim is taller than Tom. Tom is

2m tall. Therefore, Jim is taller than 2m.”

139

P1.

L(x,y,p

,a,g,k)ΠL(z,y,p

,a,g,k).⊃. p

∧q

P2.

L(x,y,p

,a,g,k)•L(z,y,p

,a,g,k)⊃. q

P3.

L(x

,y,z

,a,g,k)ΠL(x

,a,g,k).

⊃

.L(x

,y,p

,a,g,k)

P4.

L(x

,y,p

,a,g,z)ΠL(x

,z,q,q,a,g,k).⊃

.L(x

,y,p

,a,g,q)

It is quite subjective how to articulate a locus, which can be formulated as P5 and

P6, so called, ‘Postulates of Arbitrariness in Locus Articulation’. These postulates

affect the process of conceptualization on a word based on its referents in the world

and moreover they are very useful for spatiotemporal inference in such a context as

“Tom flied from Tokyo to Nagoya and consecutively from Nagoya to Osaka. There-

fore, he moved from Tokyo to Osaka” and “Tom moved from Tokyo to Osaka.

Therefore, he passed somewhere (between the two places)”, respectively.

P5.

(∀p,q,r,k)(∃k’)L(y,x,p,q,a,g,k)•L(y,x,q,r,a,g,k).⊃

.L(y,x,p,r,a,g,k’)∧k’≠k

P6.

(∀p,r,k)(∃q,k’)L(y,x,p,r,a,g,k).⊃

.L(y,x,p,q,a,g,k’)•L(y,x,q,r,a,g,k’)∧k’≠k

A perceptual locus can be formulated with atomic locus formulas and temporal

conjunctions such as SAND (

∧

or Π) and CAND (∧

or •). This is not necessarily the

case for a conceptual locus corresponding to such a generalized mental image or

knowledge piece. For example, people usually interpret the construction ‘B happens

before A happens’ as a general causality, namely, as ‘If A happens, B happens in

advance’. Whereas this should be formulated with logical connectives other than

conjunctions also involved, D1 is exclusively for perceptual loci so far as it is because

there is no interpreting a negated locus formula as a locus with a unique time-interval

necessary to determine a unique temporal relation

Considering such a definition as ‘A⊃B ⇔ ~A∨B (.≡.~(A∧~B))’ in standard logic,

it is not unnatural to assume the identity of a locus formula with its negative in abso-

lute time-interval, that is, negation-freeness of absolute time passing under a locus

referred to by its suppressed absolute time-interval. Therefore, in order to make D1

valid also for conceptual loci, we introduce a meta-function

defined by D5 and its

related postulates P7 and P8 as follows, where

is to extract the suppressed absolute

interval of a locus formula

D5.

δ(χ)=[t

](∈

), where χΠε([t

]).

P7.

δ(~α)=δ(α), where

is an atomic locus formula.

P8.

δ(χ)=[t

min

, t

max

], where t

min

and t

max

are respectively the minimum and the

maximum time-point included in the absolute time-intervals of the atomic

locus formulas, either positive or negative, within

140

These postulates lead to T1 (Theorem of absoluteness of time passing) below. This

theorem can read that absolute time passes during an objective event whether it may

be perceived subjectively as χ or as ~χ.

T1.

δ(~

)=δ(

)

(Proof) According to P7 and P8, the time-interval of each atomic locus formula

involved in

is negation-free and therefore so is for [t

min

, t

max

] of

(

[Q.E.D.]

The counterpart of the contrapositive in standard logic (i.e. A⊃B.≡.~B⊃~A) is giv-

en as T2 (Tempo-logical Contrapositive) whose rough proof is as follows immediate-

ly below, where the left hand of ‘:’ refers to the theses (e.g., PL is a subset of those in

pure predicate logic) employed at the process indicated by the conventional meta-

symbol ‘→’ or ‘↔’ for entailment (left-to-right or bi-directional).

T2.

⊃

.≡.~χ

⊃

-i

~χ

(Proof)

D1: χ

⊃

↔ (χ

⊃χ

)∧τ

(χ

,χ

)

PL: ↔ (~χ

⊃~χ

)∧τ

(χ

,χ

)

T1: ↔ (~χ

⊃~χ

)∧τ

(~χ

,~χ

)

D1: ↔ (~χ

⊃~χ

)∧τ

-i

(~χ

,~χ

)

D1: ↔ ~χ

⊃

-i

~χ

[Q.E.D.]

Therefore, S3 and S4 are proved to be paraphrases each other by employing T2

while S5 and S6 are proved so by the definition of tempological conjunctions (i.e.

∧

(S3) It gets cloudy before it rains.

=If it rains, it gets cloudy in advance. (≡Raining⊃

-5

Getting_Cloudy)

(S4) It does not rain after it does not get cloudy.

=Unless it gets cloudy, it does not rain later. (≡~Getting_Cloudy ⊃

~Raining)

(S5) It got cloudy before it rained. (≡Raining

∧

-5

Getting_Cloudy)

(S6) It rained after it got cloudy. (≡Getting_Cloudy

∧

Raining)

All loci in attribute spaces are assumed to correspond one to one with movements

or, more generally, temporal events of the FAO. Therefore, the L

expression of an

event is compared to a movie film recorded through a floating camera because it is

necessarily grounded in FAO’s movement over the event. And this is why S7 and S8

can refer to the same scene in spite of their appearances, where what ‘sinks’ or ‘rises’

is the FAO and whose conceptual descriptions are given as (17) and (18), respective-

ly, where ‘A

’, ‘↑’ and ‘↓’ refer to the attribute ‘Direction’ and its values ‘upward’

and ‘downward’, respectively.

(S7) The path sinks to the brook.

(S8) The path rises from the brook.

(∃y,z,p)L(_,y,p,z,A

,_)ΠL(_,y,↓,↓,A

,_)∧path(y)∧brook(z)∧z≠p

(17)

(∃y,z,p)L(_,y,z,p,A12,G

,_)ΠL(_,y,↑,↑,A

,_)∧path(y)∧brook(z)∧z≠p (18)

141

Such a fact is generalized as P9 (Postulate of Reversibility of Spatial Event (PRS)),

where χ

and χ

are a perceptual locus and its ‘reversal’ for a certain spatial event,

respectively, and they are substitutable with each other because of the property of

‘≡

’. This postulate can be one of the principal inference rules belonging to people’s

common-sense knowledge about geography.

P9.

.≡

Any matter is assumed to consist of its parts in a structure (i.e. spatial event), which

is generalized as P10 (Postulate of Partiality of Matter) here, reading that a matter x

can be perceived or deemed as a complex of matters x

and x

P10.

L(y,x

,p,q,a,G

,k)•L(y,x

,q,r,a,G

,k).≡

. L(y,x

,p,q,a,G

,k)ΠL(y,x

,q,r,a,G

,k)

This postulate and P9 are utilized for translating such a paradoxical sentence as

“The Andes Mountains run north and south.” into such a plausible interpretation as

“One part of the Andes Mountains runs north (from somewhere) and the other part

runs south”.

3 Conclusions

The deductive system is one kind of applied predicate logic (i.e., pure predicate logic

with certain domain-specific constants [14, 17-19]), but the domain-specificity in its

syntax and semantics is exclusively related to atomic locus formulas and the essential

part of its semantics is subject to their interpretation controlled by the family of do-

main-specific constants, namely, Attributes, Values, Patterns and Standards intended

to correspond well with human sensory systems. The author has found the implemen-

tation so far a success and come to have such a perspective that the scheme presented

here is applicable to various mind models for humans or humanoid robots of different

competences and performances simply by controlling such a family [20]. The expres-

sive power of L

was demonstrated with linguistic or pictorial manifestations

throughout this paper. Its most remarkable point in comparison with other KRLs

resides in that it can provide terms of the physical world such as carry, snow, etc.

with precise semantic definitions that are normalized by atomic locus formulas and

visualized as loci in attribute spaces in both temporal and spatial extents (i.e. temporal

and spatial events), which leads to good computability and intuitive readability of L

expressions. Future work will include further elaboration and validation of the formal

system and the most important problems remaining unsolved are how to provide each

attribute space and how to build its corresponding atomic performance. These prob-

lems concern neuroscience as well as psychology and therefore the author will con-

sider employment of soft computing theories such as neural network, genetic algo-

rithm, fuzzy logic, etc. for their self-organization in the near future.

At last of this paper, the author would like to acknowledge that this work was par-

tially funded by the Grants from Computer Science Laboratory, Fukuoka Institute of

142

Technology and Ministry of Education, Culture, Sports, Science and Technology,

Japanese Government, numbered 14580436 and 17500132.

References

1. Yokota,M.: An Approach to Natural Language Understanding Based on Mental Image

Model. In Sharp,B. (ed.), Natural Language Understanding and Cognitive Science.

INSTICC PRESS (2005) 22-31.

2. Yokota,M.& Capi,G.: Cross-media Operations between Text and Picture Based on Mental

Image Directed Semantic Theory. WSEAS Trans. on Information Science and Applica-

tions, 10-2 (2005)1541-1550.

3. Coradeschi,S. & Saffiotti,A.: An introduction to the anchoring problem. Robotics and

Autonomous Systems, 43 (2003) 85–96.

4. Drumwright,E. Ng-Thow-Hing,V. & Mataric,M.J.: Toward a vocabulary of primitive task

programs for humanoid robots. Proceedings of International Conference on Development

and Learning (ICDL), Bloomington, IN (May 2006).

5. Woods,W.A.: What's in a Link: Foundations for Semantic Networks. In Representation and

Understanding, Studies in Cognitive Science. New York: Academic Press (1975) 35-82.

6. Dorr,B.& Bonnie,J.: Large-Scale Dictionary Construction for Foreign Language Tutoring

and Interlingual Machine Translation. Machine Translation, 12-4 (1997) 271-322.

7. Zarri,G.P.: NKRL, a Knowledge Representation Tool for Encoding the Meaning of Com-

plex Narrative Texts, Natural Language Engineering. Special Issue on Knowledge Repre-

sentation for Natural Language Processing in Implemented Systems, 3 (1997) 231-253.

8. Lenat, D.: CyC: A Large-Scale Investment in Knowledge Infrastructure, Communications

of the ACM (1996).

9. Leisi,E.: Der Waltinhalt-Seine Struktur im Deutschen und Englischen-, Quelle & Meyer,

Heidelberg (1961).

10. Noton,D.: A Theory of Visual Pattern Perception, IEEE Trans. on Systems Science and

Cybernetcs, SSC-6,4 (1970) 349-357.

11. Gardenfors,P: Conceptual Space, MIT Press (2000).

12. Langacker,R.: Dynamicity, fictivity, and scanning: The imaginative basis of logic and

linguistic meaning. In Precher, Diane and Rudolf A. Zwaan (eds.), Grounding Cognition:

The Role of Perception and Action in Memory, Language and Thinking. Cambridge: Cam-

bridge University Press (2005) 164-197.

13. Roget,P.: Thesaurus of English Words and Phrases, J.M.Dent & Sons Ltd., London (1975).

14. McDermott,D.V.: A temporal logic for reasoning about processes and plans. Cognitive

Science, 6 (1982) 101-155.

15. Allen, J.F.: Towards a general theory of action and time. Artificial Intelligence, 23-2

(1984) 123-154.

16. Shepard, R.& Metzler. J.: Mental rotation of three dimensional objects. Science, 171(972):

701-3 (1971).

17. Shoham,Y.: Time for actions: on the relationship between time, knowledge, and action.

Proceedings of IJCAI\89, Detroit, MI (1989) 954-959.

18. Kabanza,F., 1995. Synchronizing multiagent plans using temporal logic specifications,

Proceedings of 1st International Conf. on Multi-Agent Systems (ICMAS-95), pp.217-224.

19. Haddawy,P.: A logic of time, chance, and action for repesenting plans. Artificial Intelli-

gence, 80-2 (1996) 243-308.

20. Shiraishi,M, Capi,G.& Yokota,M.: Human-robot communication based on a mind model.

Artificial Life and Robotics (2005) 136-140.

143