A HYBRID SET-UP OPTIMIZATION MODEL

FOR TANDEM COLD ROLLING MILL

Mohammad Hadi Mirmohammadi, Hossein Haddad

Department of CRM Automation Engineering, Mobarakeh Steel Company, Isfahan, Iran

Seyed Mehdi Naghavi

Department of Tandem Cold Rolling Mill, Mobarakeh Steel Company, Isfahan, Iran

Keywords: Hybrid optimization, Real-coded genetic algorithm, Nelder and Mead simplex method, Set-up optimization

model, Tandem cold rolling.

Abstract: Set-up optimization of the rolling process involves several parameters that may lead to complex multi

objective optimization problem. Also, it is well known that experience is playing a vital role in the selection

of operating parameters in rolling mill. This paper presents a combination of two optimization procedure for

a multi objective optimization problem. The first optimization phase is based on Nelder and Mead simplex

method which focus on balance of power, force and reduction distribution in set-up planning. Then, a real-

coded genetic algorithm based optimization procedure applies on the system as an outer loop to optimize

energy consumption and productivity. An experimental result of application to five stand tandem cold

rolling mill is presented.

1 INTRODUCTION

Process optimization is the discipline of adjusting a

process so as to optimize some specified set of

parameters without violating some constraint. The

most common goals are minimizing cost,

maximizing throughput, and/or efficiency. This is

one of the major goals in industrial automation

systems.

The optimization of manufacturing and product

quality is possible when the effect of each process

stage and its influence on the process parameters are

known as a process model and an advanced

architecture of optimization mechanism apply on

this model to achieve optimized parameters.

Recently, a lot of attention has been devoted

toward advanced techniques of computational

intelligence for Process optimization. However it is

well known that experience is playing a vital role in

modelling and optimization of complex industrial

processes (Venkata & Suryanarayana, 2001).

The tandem cold rolling of metal strip is a

complex nonlinear multivariable process whose

optimization presents significant challenges to the

control design.

Set-up optimization and Scheduling for tandem

cold mills has been frequently investigated in the

last few years, motivated by the benefits they can

provide in terms of quality and productivity

improvements (Pires, et. al., 2006). Reductions,

speeds, tensions and forces, which must be followed

by the control loops, form the main part of the mill

set-up (Bryant, 1973). Reduction and tension

distribution is the major point for set-up calculation

that usually obtains by look-up table or some simple

formula based on experience. Therefore by this

distribution, optimal set-up may not be achieved.

Optimal schedules should result in maximized

throughput and minimized operating cost (Wang, et

al., 2000).

In the present work, recent developments will be

discussed concerning to set-up optimization applied

to a continues five stand tandem cold mill at

Mobarakeh Steel plant in Iran, which, due to more

high quality and productivity market demand, was

totally revamped in 2004. The proposed algorithm is

composed of two step optimization architecture. The

first part is an inner loop which calculates stand

reductions and inter-stand tensions based on

reduction balance, power balance and force balance.

Mirmohammadi M., Haddad H. and Naghavi S. (2009).

A HYBRID SET-UP OPTIMIZATION MODEL FOR TANDEM COLD ROLLING MILL.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,

pages 49-54

DOI: 10.5220/0002204700490054

 SciTePress

For the optimization of the set-up, Nelder and Mead

simplex algorithm has been employed. The major

goal of this part is to balance of power, force and

reduction according to rolling condition and

experience. The second part is an outer loop which

optimizes rolling productivity by using genetic

algorithm. In fact, the outer loop evaluates some

coefficient of inner optimization loop to maximize

throughput and minimized energy consumption.

The study is organized in the following manner.

First, section 2 delivers a brief introduction to the

architecture of set-up optimization based on Nelder

and Mead simplex algorithm. In section 3, we

discuss a productivity optimizer as an outer

optimization loop that applies on set-up optimization

structure described in section 2. Experimental results

are explained in section 4. finally, section 5 presents

the main conclusions.

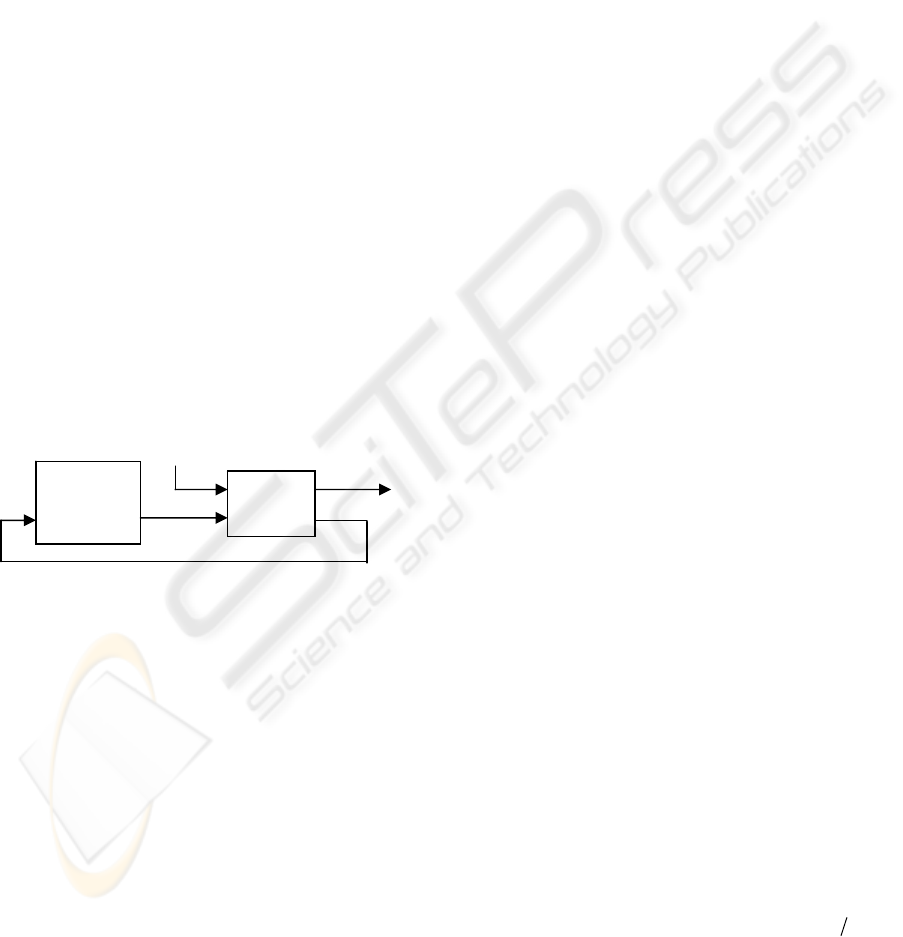
2 PRESET BALANCE MODEL

The structure of the inner loop set-up model is

presented in figure 1. The preset balance optimizer

receives the power and force of each stand and

calculates reductions and tensions. In this work the

Bryant model is considered for rolling mill process

model (Bryant, 1973).

Figure 1: Inner loop set-up model.

The process of set-up calculation consists of

power balancing, force balancing and reduction

balancing. To balance the power, the required per

unit power of each stand should be the same, taken

the total available power of the rolling mill as the

base power. Thus, the total set-up power should not

be greater than the nominal power of the rolling

mill. In force balancing the applied forces should be

smoothly distributed through the first stands in order

to avoid flatness problems. Furthermore, the last

stand force is critical due to imposed quality

purposes like roughness and flatness. The reduction

balancing is based on experience and usually is

formed as a look-up table.

The specific tension applied to the strip on each

zone should not be greater than one third of the yield

strength of the strip on that zone (Bryant, 1973).

Furthermore, the distribution of specific tension

through the zones should follow the same law as the

distribution of reduction through the stands in order

to avoid unbalancing of back and front tension on

any stand. Also, it is desirable that the stand

maximum set-up speed be achieved using the total

available power of that stand (Pires, et al., 2006).

To achieve the goals which described we should

define a suitable objective function and employ a

powerful optimization algorithm. Nelder and Mead

simplex method is one of the best algorithm for

optimization that is applied in several application

related to cold mill set-up optimization.

A detailed description of the simplex method can

be found in the work of Pires, et al. (2006). The

simplex method, considers the unconstrained

minimization of a nonlinear cost function

(

)

xxxfJ ,,,

…

of n variables, without

evaluating its derivatives. The minimization step is

variable according to the cost function. Briefly

speaking, disturbances are introduced in the initial

values of

x and new values of the cost function are

calculated, corresponding to each disturbance. Three

operations may be accomplished, according to the

following steps: reflection, contraction and

expansion.

The iterative process is initiated sorting the

points

xx , and

x for which the function has its

maximum value

J , the second maximum value

J , and the minimum value

J , respectively.

The average point or centroid

x is determined

finding the average of all points

, except

. From

equation 1 and assuming the minimization step

b ,

it results

xx =

, known as reflection of

with

respect to

x .

(

)

WCC

xxbxx −+= (1)

The following four cases can then occur:

 If

J <

J , then

x is replaced by

and the process is restarted;

 If

J <

J , then set 2=b and get

known as expansion of

x with respect to

x .

is replaced by

and a new

process is started;

 If

, a contraction is made,

generating a vertex

xx = for which 21=b . If

J <

J ,

x is replaced by

x and a

new process is started;

Reductions,

Tensions

Process

Model

Preset

Balance

Optimizer

Powers, Forces

Set-up

PDI

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

 If

, a contraction with change in

direction must be done, generating a vertex

xx = for which 21

−

b . If

J <

J ,

x is

replaced by

and a new process is started.

The simplex method requires a starting point not

so distant of the optimum point as a condition to

converge; the use of empirical laws during

initialization or using beta factor algorithm which is

described in Pires, et al. (2006) help to reach this

objective. From this point, the simplex method

calculates the initial cost function and allow for

disturbance in reductions and tensions, which result

in new values of power, forces and tensions and

subsequently in new value for the cost function.

In order to define a suitable objective function

for the tandem mill, power, force, reduction and

tension were assumed to be the most important

variables to form the objective function. Therefore,

the objective function was then conceived as:

∑∑∑∑

====

+++=

1ij

JJkJkJkJ (2)

Where

is the power balance cost function,

J is force balance cost function and

J is the

reduction balance cost function of stands i = 1, 2, 3,

4, 5, respectively.

J is the tension balance cost

function of zones

j = 1, 2, 3, 4 between two

consecutives stands.

k ,

k and

k present the weight of each cost

function of the objective function. We will see later

that these coefficients come from the outer

optimization loop.

The cost function of power, force, reduction and

tension are given by

⎟

⎠

⎞

⎜

⎝

⎛

−

minmax

(3)

⎟

⎠

⎞

⎜

⎝

⎛

−

minmax

(4)

⎟

⎠

⎞

⎜

⎝

⎛

−

minmax

(5)

⎟

⎠

⎞

⎜

⎝

⎛

−

minmax

(6)

N ,

N and

K ,

K are exponents

and coefficients of cost functions of power, force

and tension, respectively. The maximum and

minimum limits for power (

max

P and

min

P ), force

(

max

F and

min

F ), reduction (

max

R and

min

R ), and

tension (

max

T and

min

T ), are normally defined

based on the process analyst knowledge. The

objective function is strongly penalized if

P <

min

or P >

max

P for power and also there is the same

situation for force, reduction and tension.

The algorithm described above is executed

several times until a minimum value for the cost

function is reached. The criterion for stopping this

process is the number of iterations or a given

incremental reduction of cost function between two

consecutive iterations. Consequently one set of

reduction and tension distribution will be achieved

that will be used in other set-up values calculation.

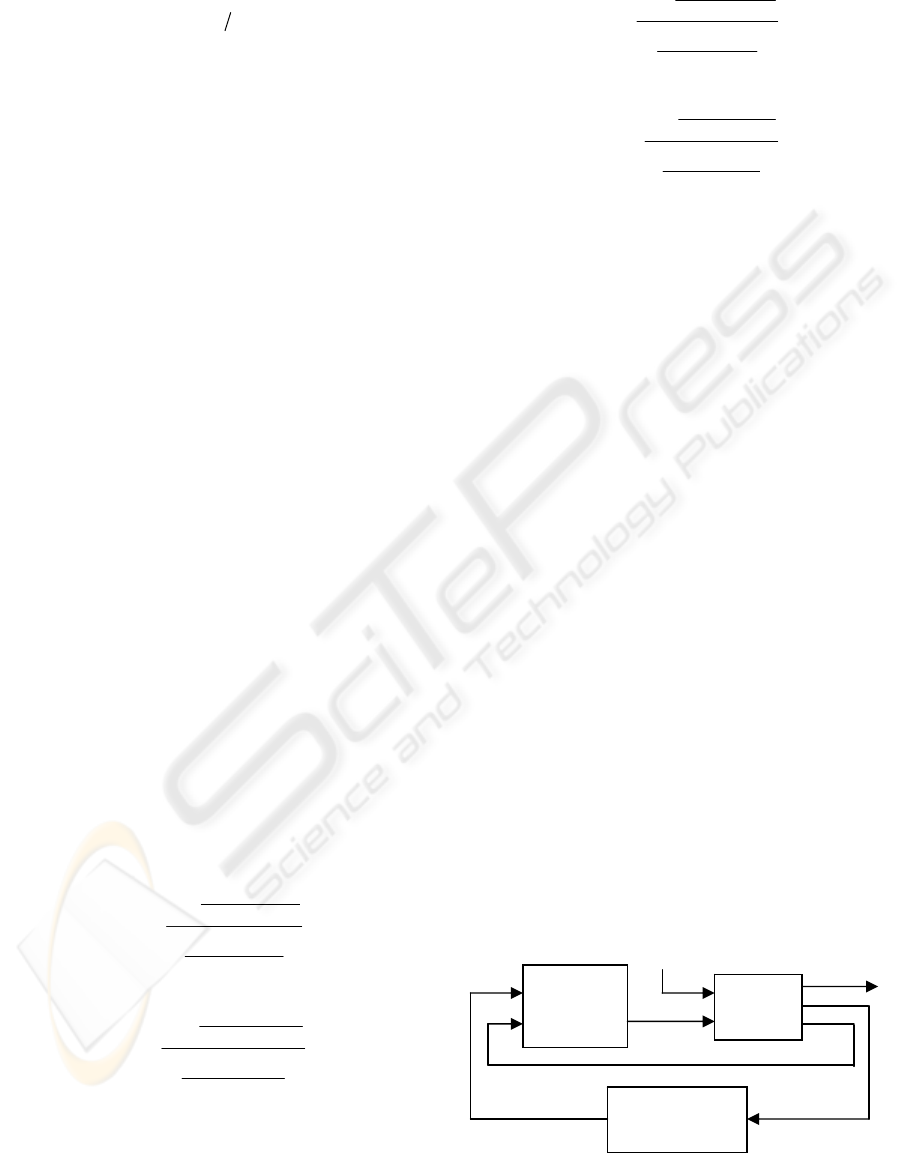
3 HYBRID SET-UP MODEL

In section 2, the optimization was done to balance

the main parameters of rolling but it doesn’t

guarantee to maximize throughput and efficiency. So

in this paper, we present an additional optimization

loop as an outer loop using genetic algorithm to

optimize energy consumption and rolling speed.

Figure 2: Hybrid set-up model.

Productivity

Optimizer

Reductions,

Tensions

Process

Model

Preset

Balance

Optimizer

Powers, Forces

Energy, Speed

KKK ,,

Set-up

PDI

A HYBRID SET-UP OPTIMIZATION MODEL FOR TANDEM COLD ROLLING MILL

Figure 2 shows the structure of hybrid

optimization method. The required energy and

rolling speed are feedback parameters from process

model and is used in productivity optimizer. The

outputs of this optimizer are

k ,

k and

k which

is used as coefficients of objective function in

balance optimization. To minimize energy

consumption and maximize rolling speed we

consider the objective function as:

(

)

(

)

∑

−+=

max

. vvEJ

βα

(7)

In this equation,

E demonstrate required energy

consist of reduction and tension energy and evaluate

by rolling energy model. The parameter

v is the

maximum allowable rolling speed corresponding to

reduction distribution and power of motors.

Genetic algorithms (GAs) are gradient free

parallel-optimization algorithms that use a

performance criterion for evaluation and a

population of possible solutions to search for a

global optimum. These structured random search

techniques are capable of handling complex and

irregular solution spaces (Setnes & Roubos, 2000).

GAs are inspired by the biological process of

Darwinian evolution where selection, mutation, and

crossover play a major role. Good solutions are

selected and manipulated to achieve new and

possibly better solutions. The manipulation is done

by the genetic operators

that work on the

chromosomes in which the parameters of possible

solutions are encoded. In each generation of the GA,

the new solutions replace the solutions in the

population that are selected for deletion.

We consider real-coded GAs. Binary coded or

classical GAs are less efficient when applied to

multidimensional, high-precision or continuous

problems. The bit strings can become very long and

the search space blows up. Furthermore, central

processing unit (CPU) time is lost to the conversion

between the binary and real representation. Other

alphabets like the real coding can be favourably

applied to variables in the continuous domain. In

real-coded GAs, the variables appear directly in the

chromosome and are modified by special genetic

operators. Various real-coded GAs were recently

reviewed in Herrera and Lozano (1998).

The chromosome representation determines the

GA structure. We encode the parameters of outer

loop in a chromosome as Eq. (8) where

Ll ,,1 

and

is the size of chromosomes population.

[]

RlFlPll

KKKS ,,=

(8)

The selection function is used to create well-

performing chromosomes which have a higher

chance to survive. The roulette wheel

selection

method is used to select

chromosomes for

operation.

Two classical operators, simple arithmetic

crossover and uniform mutation

and four special

real-coded operators are used in the GA. These

operators have been successfully applied in the work

of Setnes and Roubos (2000) and

Michalewicz (1994).

For crossover operations, the chromosomes are

selected in pairs. In Simple arithmetic crossover two

chromosomes are crossed over at the random

position. Whole arithmetic crossover creates a linear

combination of two chromosomes as:

()

SrSrS

.1.

−+=

(9)

In this section,

[

]

1,0

∈

r and is a random number.

Heuristic crossover is another kind of a pair

chromosomes combination such that:

(

)

()

SSrSS

−+=

(10)

For mutation operations, single chromosomes

are selected. In Uniform mutation a random selected

element is replaced by a random number in the range

of element. Multiple uniform mutations is uniform

mutation of

randomly selected elements and in

Gaussian mutation all elements of a chromosome are

mutated such that a random number drawn from a

Gaussian distribution with zero mean will be added

to each element.

In this paper the chance that a selected

chromosome is used in a crossover operation is 95%

and the chance for mutation is 5%. When a

chromosome is selected for crossover (or mutation)

one of the used crossover (or mutation) operators are

applied with equal probability. The search space of

elements in chromosomes is determined in the range

between 0 and 1.

4 EXPERIMENTAL RESULTS

As an experimental work, we implemented the

described algorithm on five stand tandem mill of

Mobarakeh Steel plant, Iran. In the first step, the

Preset Balance Model was implemented to produce

optimal set-up values based on objective function

presented in Eqs. (2)-(6) by using the values for the

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

Table 2: Optimization results using Preset Balance Model and Hybrid Set-up Model.

Preset Balance Model Hybrid Set-up Model

Red.

(%)

Tens.

(ton)

Speed

(mpm)

Force

(ton)

Power

(kw)

Energy

(kwh/t)

Red.

(%)

Tens.

(ton)

Speed

(mpm)

Force

(ton)

Power

(kw)

Energy

(kwh/t)

Zone 0 13 273 13 288

Stand 1 28.8 865 1724 4.29 32.4 949 2656 6.26

Zone 1 25.9 383 22.7 427

Stand 2 28.4 890 4560 11.35 26.7 1074 4560 10.74

Zone 2 19.4 535 18.85 582

Stand 3 26.1 854 4487 11.18 24 846 4300 10.12

Zone 3 16.83 723 16.82 766

Stand 4 21.1 876 4481 11.15 20.1 795 4375 10.29

Zone 4 16.72 917 16.95 957

Stand 5 5.36 570 1831 4.58 7 623 2103 4.95

Zone 5 2.86 969 2.85 1029

Total 42.55 42.36

coefficients and exponents adjusted for each stand

that are presented in Table 1. Adjustment of these

coefficients has been done by focus on a regular

distribution of reductions, power and forces based

on rolling situation and experience.

Table 1: Exponents and coefficients of cost functions.

Std.1 Std.2 Std.3 Std.4 Std.5

1 1 1 1 1

18 18 18 18 10

0.001 0.001 0.001 0.001 1

18 18 18 18 18

1 0.1 0.1 0.1 1

10 10 10 10 10

1 1 1 1 -

5 5 5 5 -

For the second phase, the hybrid set-up model

with proposed objective function in Eq. (7) was

implemented. We apply a real-coded GA with the

population size (

) equal to 20 and 5

n for

operation in each iteration. The chance of crossover

operation is 95% and for mutation is 5%.

The values summarized in Table 2 show the final

result of set-up calculation according to the preset

balance model in the right side and hybrid set-up

model in the left side of table.

By using preset balance model, the balance of

power, force and reduction is obtained after

approximately 100 iteration but the maximum

obtained speed value will be 969 (m/min) while the

total required energy is equal to 42.55 (kwh/t).

The implementation of the hybrid set-up model

produced, as shown in the right part of Table 2, a

significant improvement for the global performance.

The rolling speed will increase to 1029 (m/min) and

the required energy will decrease to 42.36 (kwh/t).

However the balance of power, force and reduction

is a little changed but we can obtain more

throughputs by using less energy that provide higher

productivity.

5 CONCLUSIONS

In this paper we have described a hybrid

optimization procedure for set-up generation of

tandem cold rolling mill. In order to complexity of

rolling process and the role of experience in this

process, we should solve a multi objective problem

to calculate optimum set-up values. So, we has

presented a hybrid algorithm consists of two

optimization model.

The preset balance optimization model is based

on Nelder and Mead simplex method which

optimizes the balance of power, force and reduction

of stands. The simplex method, considers the

unconstrained minimization of a nonlinear cost

function, without evaluating its derivatives. By using

empirical laws and beta factor algorithm we can find

starting point not so distant of the optimum point

which helps us to reach the optimum solution in a

few iteration.

The hybrid set-up model appears as an outer loop

which minimizes the energy consumption and

maximizes rolling speed through evaluation of

coefficient of objective function related to preset

balance model.

The optimization algorithm used in this model is

based on Genetic algorithm and to increase the

A HYBRID SET-UP OPTIMIZATION MODEL FOR TANDEM COLD ROLLING MILL

efficiency and decrease the processing time, we have

proposed a real-coded genetic algorithm which

employs some special kind of crossover and

mutation operation to reduce the calculation time.

The proposed optimization approach was

successfully applied to five stand tandem cold

rolling mill, located at mobarakeh steel plant of Iran.

Experimental results show that the obtained set-up

leads to high quality and productivity in the tandem

cold mill.

REFERENCES

Pires, C. T. A., Ferreira, H.C., Sales, R.M., and Silva,

M.A., (2006) ‘Set-up optimization for tandem cold

mill: A case study’, Journal of Materials Processing

Technology, vol. 173, pp.368-375, ELSEVIER Press.

Setnes, M., Roubos, H., (2000) ‘GA-Fuzzy Modelling and

Classification: Complexity and Performance’, IEEE

Transactions on Fuzzy Systems, vol. 8, no. 5, October,

pp. 509-522.

Michalewicz, Z., (1994) Genetic Algorithms + Data

Structures = Evolution Programs, 2nd edition, New

York: Springer-Verlag.

Herrera, F., Lozano, M. and Verdegay, J. L., (1998)

‘Tackling real-coded genetic algorithms: Operators

and tools for behavioural analysis’, Artificial

Intelligence Rev., vol. 12, pp. 265–319.

Venkata, R.N., Suryanarayana, G., (2001) ‘A set-up model

for tandem cold rolling mills’, Journal of Materials

Processing Technology, vol. 116, October, pp. 269-

277, ELSEVIER Press.

Wang, D. D., Tieu, A. K., De Boer, F.G., Yuen, W. Y. D.,

(2000) ‘Toward a heuristic optimum design of rolling

schedules for tandem cold rolling mills’, Engineering

Applications of Artificial Intelligence, vol. 13, August,

pp. 397-406, ELSEVIER Press.

Bryant, G. F., (1973) Automation of Tandem Mills,

London: Iron and Steel Institute.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics