COOPERATIVE UAVS MAPPING COMPLEX ENVIRONMENT

USING 2D SPLINEGON

Samuel B. Lazarus, Antonios Tsourdos, Brian A. White, Rafał

Zbikowski and Peter Silson

Department of Informatics & Sensors, Cranﬁeld University

Defence Academy of the United Kingdom, Shrivenham, U.K.

Keywords:

Multiple sensor fusion, Circle Packing, Path planning, Integrated GPS/INS navigation, Obstacle and collision

avoidance, Splinegon, Boundary estimation and Data association.

Abstract:

This paper presents a novel approach which enables multiple UAVs to efﬁciently explore an unknown envi-

ronment and incrementally build the map of the area and its complex shaped obstacles, represented here as

concave and convex in shape. The task is achieved by a improved performance of sensor based searching,

navigation and mapping of these complex shaped obstacles in an unknown environment. The improved per-

formance is quantiﬁed by explicit bounds of navigating the UAVs using an extended Kalman ﬁlter and to build

the map of the complex shaped obstacles using the 2-D Splinegon. The circle packing search algorithm is used

for the completeness of coverage in searching the unknown obstacles regions and the UAVs trajectories are

generated by the Dubins path planning algorithm. This novel proposed algorithm results in a robust approach

to search and map the obstacles using multiple UAVs that is also computational attractive.

1 INTRODUCTION

This paper focusses on swarm of UAVs deployed for

a mission of searching an unknown region to detect

obstacles and to extract their shape. The circle pack-

ing search algorithm (Kershner, 1939), (Guo and Qu,

2005) is implemented where the search is carried out

by a sequence of “looks” each of which covers a circle

corresponding to the footprint of the sensor on board.

This circle pacing algorithm covers the plane by pack-

ing each circles into the unknown environment. The

centers of each of this packed circles represent the

way points to be used on path planning of the UAVs.

A mission planning algorithm is described which en-

ables the UAVs to switch between the searching mode

and the mapping of the detected obstacle. Since the

swarm of UAVs ﬂy around an unknown environment,

a sense and avoid system is developed so the UAVs

autonomously replan their paths when they approach

an obstacle or predict intersection of air trafﬁc. Thus

the system presented here provides a safe surveillance

of unknown areas by swarm of UAVs. Furthermore

the proposed mission planning not only enables the

swarm of UAVs to switch from searching mode into

mapping mode, but also ensures the allocation of the

required number of UAVs to map that obstacle with

in searched region.

In the fulﬁllment part of the mapping task, the

measurements from laser sensor that are mounted on

the UAVs is the only source to construct the map of

the detected obstacle. This strongly suggests that the

most efﬁcient way in modelling approach should be to

deﬁne these measurement points as vertices that can

form a polygon with line segments. This raises an is-

sue as to how to represent the curved nature of these

obstacles. One such promising approachis introduced

in this paper that uses a generalization of polygons

that produces a set of vertices that are connected by

line segments of constant curvature. This is a sub-

set of a class of objects named as splinegons (Dobkin

et al., 1988), (Dobkin and Souvaine, 1990).

In the mapping process the fused EKF estimated

positions are used with the limited number of mea-

surements (i.e. required number of the the interpola-

tion points) from the laser sensors to build the map.

As the vehicles ﬂy around the obstacle, sensors such

as laser sensors are used to measure the distance to

the obstacles. Out of all these measurements, only a

carefully selected number of measurements are cho-

sen which represent the required vertices to construct

a simple polygon. The data association algorithm is

implemented to select a limited number of vertices

and to uniformly distribute these vertices around the

obstacle in a computationally efﬁcient way. This se-

413

Tsourdos A., White B., Lazarus S., Silson P. and

Zbikowski R. (2009).

COOPERATIVE UAVS MAPPING COMPLEX ENVIRONMENT USING 2D SPLINEGON.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 413-416

DOI: 10.5220/0002204804130416

 SciTePress

lection of maximum number of vertices that can form

a polygon is limited from sixteen to twenty vertices.

This selection of vertices is accomplished by calcu-

lating the length and the curvatures between each of

the vertices and to eliminate the vertex that has a min-

imum length and curvature. The selection process is

based on the size and the curved nature of the obsta-

cle. Thus, the constructed polygon is generalised to

produce a set of vertices that are connected by line

segments of constant curvature called splinegon. This

splinegon is a set of vertices that have constant cur-

vature line segments deﬁned with C

contact at the

vertex points.

1. The prediction of next way points for the search

algorithm and prediction of a new way points

when obstacle/collision avoidance algorithm is

activated.

2. Switching between the search mode into the map-

ping the unknown obstacle and predict the way

points and its orientation to get the measurements.

3. The prediction of the required number of vehicle

to accomplish the mapping task (How many vehi-

cle is needed to complete the mission?)

4. If more then one UAV is used for the mapping

task,

(a) Find a shortest way points for the other UAVs

to reach the mapping region.

(b) Whether the UAVs needs to exchange the infor-

mation with one to another, and

single or multiple, depending upon the intersec-

tion detection between the local updates. Even-

tually, the global update is performed between

the intersection detected UAVs.

5. The prediction of required number of measure-

ment for the mapping from each of the detected

obstacles.

This newly proposed algorithm gives a solution that

has a highly richness in building the curved nature

of the unknown obstacle in an unknown environment.

This proposed approach is a computationally attrac-

tive one resulting in information driven mission plan-

ning and the mapping of unknown environments with

limited measurements.

The development of this algorithm is shown in the

functional block diagram in ﬁgure 1.

EKF based

Localisation

INS

Measurements

GPS

Measurements

Vertex Selection and

Data Association

TOF Laser sensor

Measurements

Constructing the Polygon

with Line Segments

Mapping the obstacle

using 2-D Splinegon

Yes

Predicting the next way

points for mapping

Unknown Environment

with Unknown Obstacles

Circle Packing

Algorithm

Prediction of

way points

Initial position

of the vehicles

Trajectory Generation

using Dubins Algorithm

Obstacle\Collision

Avoidance Algorithm

Search for obstacles

Decision Making

Algorithm

Switch Between

Searching & Mapping

Required number of the

vehicles for Mapping

Prediction of next

way points for search

Choosing the shortest way

points for mapping

Required number of the

measurements for Mapping

Prediction of new

way points

Sensor Fusion

Figure 1: The functional block diagram.

2 PATH PLANNING AND CIRCLE

PACKING ALGORITHM

The path planning algorithm generates a ﬂyable and

safe path to the UAVs to ﬂy from one location to an-

other. The locations are predeﬁned by the way-points.

The starting location is called base and the ﬁnal loca-

tion to be reached is called target. The Dubins set of

paths is used to connect the base and target by a se-

quence of successive way-points. The base and the

target are characterized by the poses, in a set of posi-

tion coordinates (x,y) and orientation θ of the UAVs.

Considered that an initial pose P

,θ

) at the base

and a ﬁnal pose at the target P

,θ

) are given,

the path r(t) connecting the two poses can be a sin-

gle or a composite curve. A path represented by a

curve in 2D is completely determined by its curvature

(Kreyszig, 1991) and the maximum curvature bound

of the UAV by κ

max

and other constraints by

∏

; then

the path planning can be mathematically represented

as:

,θ

)

r(t)

−→P

,θ

), κ(t) < κ

max

∏

(1)

Extending the equation (1) for a group of UAVs, this

changes into:

,θ

)

(t)

−→ P

,θ

)

(t) < κ

i,max

and

∏

(2)

where κ

(t) is the curvature, κ

i,max

is the maximum

curvature bound of i

path, and i = 1...N, N is the

number of UAVs. This path planning algorithm is in-

tegrated with an obstacle and Collision avoidance sys-

tem to generated the trajectories for each UAVs and

to protect the ﬂying UAVs from any collision with the

surrounded obstacles or with the on coming UAVs.

This algorithm is applied online while the UAVs are

in motion.

The circle packing algorithm (Washburn, 1981) is

to attempt to cover the given plane by packing the

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

414

circles of radius R. In other words ﬁnding a mini-

mum number of circles with the radius of R to com-

pletely cover in the given area of search. This is ac-

complished by ﬁxing the coverage range or the sensor

range are represented as a circle. The key problem

is to determine the required number of circles with a

radius R to cover the given area. This in turn pro-

duced many solutions to this problem. But the objec-

tive is to ﬁnd an optimal solution to minimise the re-

peated search. One such algorithm that was reported

in (Kershner, 1939) and (Guo and Qu, 2005) is imple-

mented here so as to covert the whole area to perform

the searching task.

The solution to optimally place the minimum

number of circles can be described as the circle has

the radius of R

and the ares to covered with this cir-

cle is denoted as W. A pattern is composed of a string

of circles with radius R

that has to placed along the

vertical line, and the distance between the centers of

any of the two adjacent circles is

√

. The m col-

umn of circles are place that are oriented parallel to

the Y −axis and the in the same way the distance be-

tween the centers of any of the two adjacent circles is

1.5R

. The origin [x

] is chosen at the left bottom

of the given areaW. This in turn enable to place the m

circles that are parallel to the y−axis which contains

the n number of circles to completely cover the given

area. So the center [x

] of the k

row (1 ≤ k ≤n)

and the l

column (1 ≤ l ≤ m) can be deﬁned viz:

] =











+ (l −1)3/2R

, y

+ (k −1)

√

]

if l is an odd integer

+ (l −1)3/2R

, y

√

3/2R

+(k−1)

√

]

if l is an even integer

(3)

So, the required number of circles needed in each

of the column and row m and n can be deﬁned as fol-

lows:

m =







Int



1.5R



+ 1, if Rem



1.5R



≤

Int



1.5R



+ 2, if Rem



1.5R



(4)

n =











Int



√



+ 1, if Rem



1.5R



≤

Int



√



+ 2, if Rem



1.5R



(5)

Where, x

and y

is the length of the environment

along X −axis and Y −axis respectively. I is an in-

teger number and Rem is the reminder of the number,

in which Rem = x−Int(x). So by applying the above

equations the required number of circles for each of

the row and column is obtained (Kershner, 1939). The

prediction of a set next way-points to start the map-

ping task is performed that would generate a set of

way points for each UAVs from its current location to

reach the starting point of the mapping task.

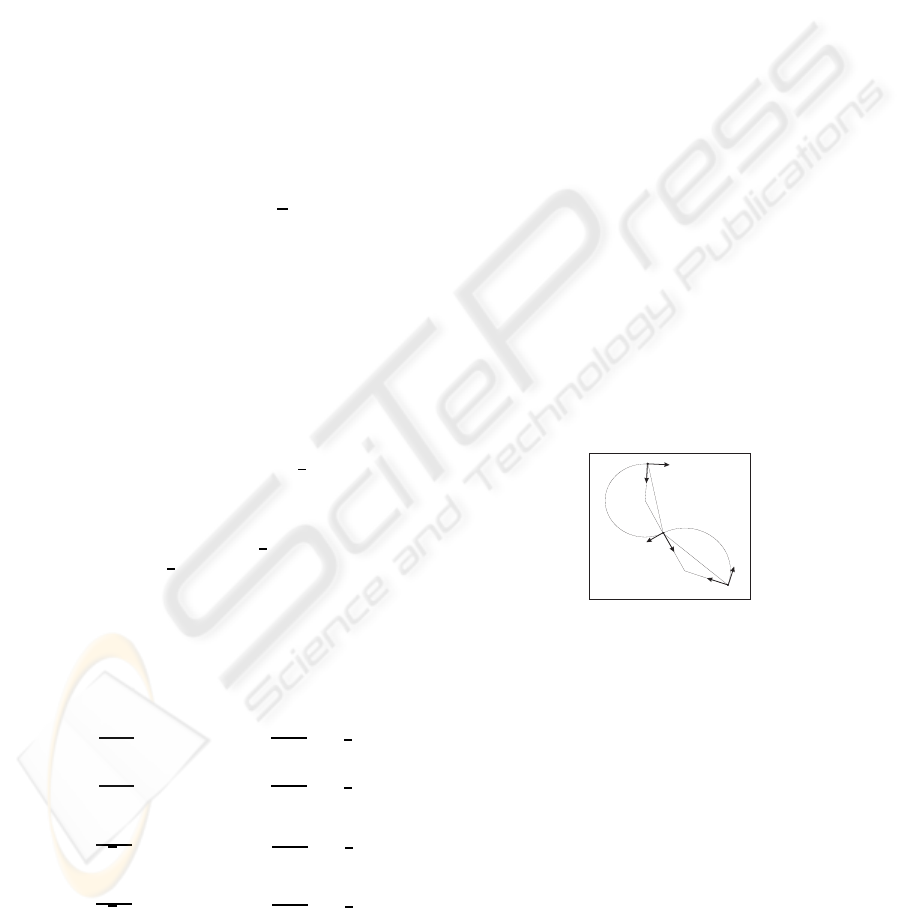
3 DEFINITION OF 2D

SPLINEGON

A Splinegon with constant curvature line segments

can be deﬁned with C

contact at the vertices. This

implies that the line segments share both a common

vertex and that the tangents at the vertices are also

the same. In order to ensure C

contact between ver-

tices, the line segments must meet both position and

tangent end point constraints. A single arc segment

between vertices only has one degree of freedom: the

arc curvature. This is not enough to be able to match

the tangent constraint at both end vertices, as at least

two degrees of freedom are necessary. Extra degrees

of freedom are thus required to ensure the C

con-

straints were both line segments end vertices can be

met. One solution to increasing the degrees of free-

dom is to introduce an intermediate vertex such that

the line segment is replaced by two arc segments of

different curvature, as shown in ﬁgure 2. Hence two

Figure 2: Arc segment with C

contact intermediate vertex.

arcs of differing curvatures will connect the UAV ver-

tices via the intermediate vertex. In order to develop

the deﬁning equations for such a solution, the inter-

section of two constant curvature arcs at a point with

contact is considered.

4 IMPLEMENTATION

AND RESULTS

The primary objective of the current work is to be

able to search the given unknown environment with

a swarm of UAVs to detect the region of the un-

known obstacles and to extract the shape of the ob-

stacle using 2-D Splinegon technique. Initially the

COOPERATIVE UAVS MAPPING COMPLEX ENVIRONMENT USING 2D SPLINEGON

415

circle packing algorithm is implemented that would

pack the required number of circles to ﬁt in the given

environment. The search algorithm is employed with

the swarm of UAVs that would predict the next way

points in online using the neighboring way points or

it will follow the given set of POI to detect the obsta-

cles where the path of the vehicle is dictated by the

Dubins path planning algorithm. By ﬁxing the de-

tecting sensor range, if any of the UAV is not able

to reach any given next way point, or if the obstacle

avoidance algorithm is activated so as to prevent the

UAV not reaching the given way point then that cir-

cle is added into the obstacle region. Once the search

is ﬁnished, depending upon the search region each of

the following requirements are taken by the decision

making algorithm.

• Find the area of the obstacle region.

• Find the required number of UAVs to accomplish

the mapping task. This can be done based on the

area of the obstacle region.

• Generate the way point for each of the UAVs to

perform the mapping task.

• Finally, ﬁnd the shortest way points to each UAVs

to reach the starting point of the mapping task

from its current location.

As the vehicle moves each of the vehicle is localised

with an EKF. At the end of the each cycle (i.e., at

the completion of one way point) a local updated map

is constructed using the Splinegon technique. In the

case of more than one UAV is used in mapping, then

an intersection detection algorithm is implemented so

as to identify the state of the obstacle and to share the

sensor information with the other UAVs. Finally the

−100 −50 0 50 100 150

−100

−80

−60

−40

−20

100

x−coordinate in k.meters

y−coordinate in k.meters

X and Y coordinate in the map

1 2 3 4 5

66 67 68 69 70

Figure 3: The results of the circle packing algorithm.

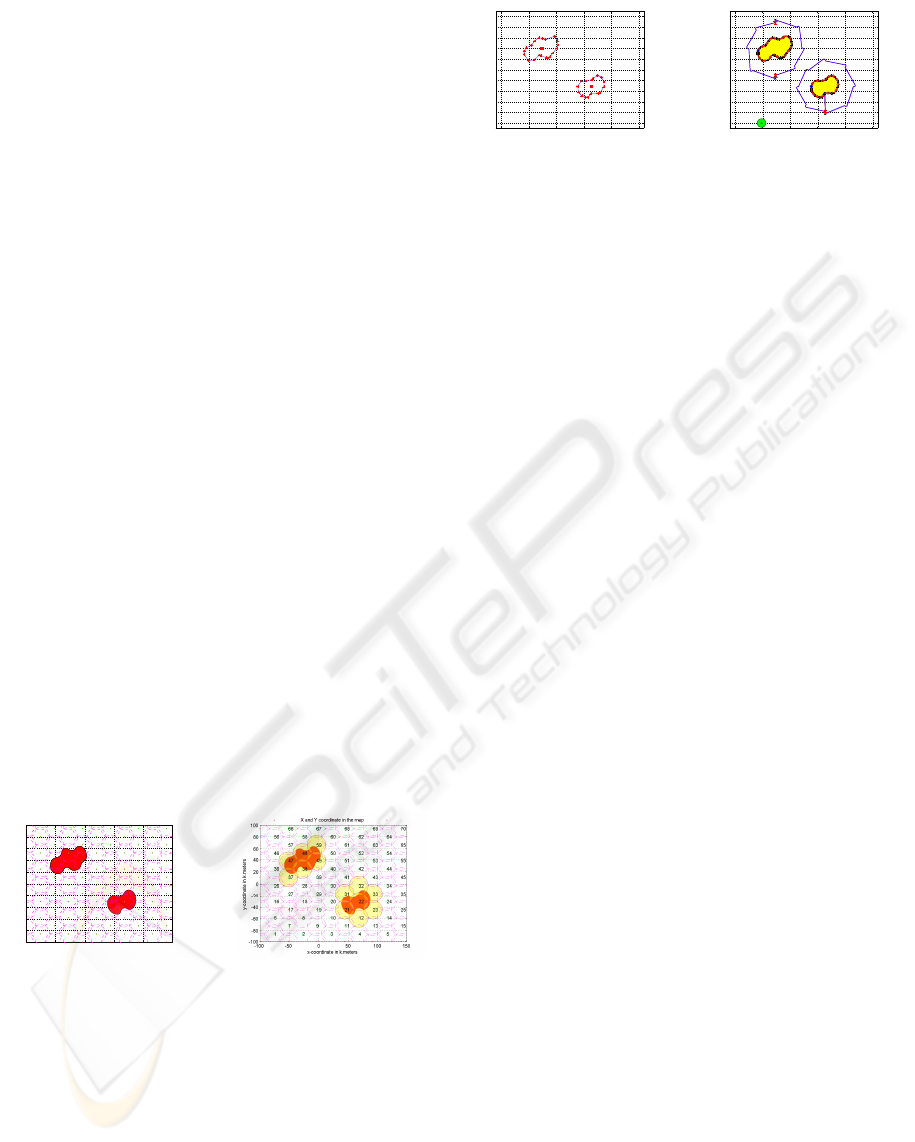
global updated map is constructed to get the map of

the unknown environment. The circles with radius R

which are packed in using circle packing algorithm

is shown in ﬁgure 2 (a). Then the search algorithm

is carried out by giving a set of point of intrust(POI)

way points to each of the UAVs so as to ﬁnd the obsta-

cle region. The shaded circles where the UAVs could

not reach are known as the obstacle region which is

shown in ﬁgure 2 (b). At the end of the search algo-

rithm, the vehicle are switched from searching mode

−100 −50 0 50 100 150

−100

−80

−60

−40

−20

100

−100 −50 0 50 100 150

−100

−80

−60

−40

−20

100

x−coordinate in k.meters

y−coordinate in k.meters

X and Y coordinate in the map

Figure 4: The ﬁnal updated map using Splinegon.

to the mapping the shape of the complex obstacle.

The local update is performed at the end of the each

way points. Finally the set of vertices that forms a

polygon with line segments in the ﬁnal update and

the global updated map of the given unknown envi-

ronment is shown in ﬁgures 4 (a) and 4 (b).

5 CONCLUSIONS

In this paper the authors have described a novel, com-

putationally attractive, approach in estimating the lo-

calisation and mapping for curvilinear objects using

multiple UAVs. It enables to map obstacles of curvi-

linear shape, the data association for the networked

sensor platforms and the reactive tasking the UAVs.

Future work will extend the Splinegon technique to

3D in the robotic network that will enable the ﬂight

paths to have even greater ﬂexibility and will enable

the complex 3D shapes to be represented by a small

set of parameters.

REFERENCES

Dobkin, D. P. and Souvaine, D. L. (1990). Computational

geometry in a curved world. Algorithmica, 5(3):421–

457.

Dobkin, D. P., Souvaine, D. L., and Wyk, C. J. V. (1988).

Decomposition and intersection of simple splinegons.

Algorithmica, 3:473–485.

Guo, Y. and Qu, Z. (2005). Coverage control for a mobile

robot patrolling a dynamic and uncertain environment.

Proceedings of the 5th world Congress on Intelligent

Control and Automation, pages 4899–4903.

Kershner, R. (1939). The number of circles covering a set.

American Journal of Mathematics, 61(3):665–671.

Kreyszig, E. (1991). Differential geometry. Dover Publica-

tions, Inc., New York.

Washburn, A. R. (1981). Search and Detection. Millitry

Applications Section Operations Research Socitey of

America.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

416