
MODELING OF CONTINUOUS FERTILIZER
GRANULATION-DRYING CIRCUIT FOR COMPUTER
SIMULATION AND CONTROL PURPOSES
Gediminas Valiulis and Rimvydas Simutis
Department of Process Control, Kaunas University of Technology, Studentų St. 48, Kaunas, Lithuania
Keywords: Granulation, Modeling, Simulation, Control.
Abstract: The paper presents the model-based approach to process simulation and advanced control in the industrial
granulation circuit of fertilizer production. Different knowledge sources, such as physical phenomena,
statistical analysis of process parameters, expert information cover different cognition domains of the
process. The mechanistic growth model developed is based on particle coating phenomena, mass and energy
transfer. The model partially takes into account the main process parameters, features and the equipment
used. Simulation has been executed to test the model performance. The model built can be used for the
evaluation of plant control methods and staff training.
1 INTRODUCTION
Drum granulation is a commonly used process in a
commercial fertilizer production. Many continuous
granulation plants operate well below design
capacity, suffering from high recycle rates and even
periodic instabilities (Wang and Cameron, 2002).
The main reasons are related to raw material
properties, process equipment and control problems.
The process control still depends on the
experience and skills of process operators, namely
experts. Diagnostic systems show potential to apply
systems engineering approaches to complex
operational problems such that operators are well
informed, are able to quickly diagnose abnormal
conditions, test quickly possible solutions via detailed
simulations and then proceed to apply corrective
actions (Salmon et al., 2007). However, a number of
interacting process variables (some of them are
stochastic in nature) lead to a complex dynamic
system that might be hard to predict and optimize
just by intuition, especially for unskilled operators.
Fortunately, it is possible to use granulation process
simulations provided by PC for the investigation of
such complex problems.
The aim of this paper is to propose the process
simulator based on an extended modeling approach
for continuous drum granulation-drying processes,
focused on simulation and control. This approach
involves the dynamic process model built from
heterogeneous knowledge sources such as physical
principles, empirical (measured) data and expert
information.
The mechanistic part incorporates the
understanding of physics and underlying
mechanisms (e.g. mass and energy balances, growth
kinetics).
The empirical part uses raw and/or filtered
process sensors’ data, their storage, retrieval and
parameter identification techniques in addition to the
mechanistic (white box) model.
The expert component involves the process
experts’ recommendations, which are of great value
due to the lack of other knowledge mentioned above.
2 MAIN PROCESS DETAILS
Drum granulation is a particle size enlargement
process often obtained by spraying a liquid binder or
slurry onto fine particles as they are agitated in a
rotary drum (Wang and Cameron, 2002). The
particle circulation is achieved mechanically (by the
action of the rotating drum and lifters). Granules are
cycled many times through the spray zone and the
liquid layer attached is pre-dried before the particle
returns to the spray zone again (Figure 1).
98
Valiulis G. and Simutis R. (2009).
MODELING OF CONTINUOUS FERTILIZER GRANULATION-DRYING CIRCUIT FOR COMPUTER SIMULATION AND CONTROL PURPOSES.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 98-103
DOI: 10.5220/0002206300980103
Copyright
c
SciTePress

Figure 1: View of the coating phenomenon.
The desired mode of granule growth is layering
(coating), resulting in very tight granule size
distributions.
A commercial continuous granulation circuit for
granulated diammonium phosphate fertilizer
(formed by the reaction of phosphoric acid and
ammonia) production consists of the following
major parts: a pipe reactor, spray nozzle system,
drum granulator-dryer, granule classifier (screens),
crusher and nuclei feed system (Figure 2).
Drum Granulator - Drier
Pipe reactor
Natural gas
Air
Furnace
External
Nuclei feed
Screens
Crusher
motor
Slurry
Product Size
Recycle feed
Undersize
Oversize
Exhaust gas
Internal
Nuclei feed
Neutralizer (H
3
PO
4
)
Gaseous NH
3
Liquid NH
3
Figure 2: Typical drum granulation-drying circuit utilized
in the diammonium phosphate (DAP) production industry.
A granulation drum is made of an inclined
cylinder with simultaneous drying (there is no
separate drying device). Drying is performed by the
heat of burned natural gas and/or reaction heat of
phosphoric acid and ammonia. Liquid DAP feed
(slurry) is sprayed onto the tumbling bed of seeds
via spraying nozzles. The drum is tilted lengthwise a
few degrees to provide the flow of granules through
the drum length. The backward screw sends a part of
granules (internal nuclei) back to the spraying zone.
Granules from the granulator-drier are transmitted to
the classifier and split into three fractions: undersize,
oversize, and marketable product size. The oversize
fraction is crushed and sent back to the granulator
together with undersize granules.
Fortunately, nowadays some important granule
size distribution variables can be measured on-line
using advanced particle size analysis systems.
Detailed and more accurate information provides the
producers of granulated materials with more data to
improve product quality and to control production
processes. Size Guide Number (SGN), related to the
median of granule population, and Uniformity Index
(UI), which shows the dispersion of population, can
be evaluated. A part of important granule size
distribution intervals can be also provided.
However, some process variables connected with
material and equipment properties can not be
evaluated and controlled directly. In such a situation
the process model can provide information about
important process states, such as recycle size flow
rate and distribution, drum system jamming factor,
granule moisture content, size evolution of single
granule inside the granulator-dryer. This information
can help to predict future process states and prevent
abnormal situations, which can initiate process
stoppage and loss of productivity.
3 MODELING
The model presented here is essentially based on
fundamental conservation principles, with partial
consideration of equipment properties and the
stochastic nature of the process. For modeling
purposes, it is necessary to divide the granulation
circuit into several balance areas with the central
component of the model – the drum granulator-drier.
There are two main processes inside the granulator-
drier: the growth of particles and moisture
evaporation (drying).
Basic modeling assumptions are:
• granule shape is spherical;
• each granule in the granulation circuit is
analyzed;
• stochastic nature of the process is estimated;
• preferred growth is by layering;
• granule agglomeration is an unacceptable mode
of operation;
• growth rate is a function of initial granule size,
slurry flow rate, temperature inside the
granulator, granule position in the drum, number
of particles in the granule bed;
• mechanical attrition of granules inside the
granulator-drier is defined by attrition function;
• presumable nucleation (formation of new seeds)
occurs during slurry spraying;
• external classification of granules into three
fractions (undersize, marketable and oversize) is
defined by classification function;
MODELING OF CONTINUOUS FERTILIZER GRANULATION-DRYING CIRCUIT FOR COMPUTER
SIMULATION AND CONTROL PURPOSES
99

• external crushing of oversize granules is
characterized by grinding function;
• residence and transportation delays in the plant
are considered;
• internal and external seeds serve as nuclei for new
granules.
3.1 White Box Modeling
There are two basic granule growth mechanisms that
act independently or in combination (Findlay et al.,
2005). A successive layering of binding material on
an initial nucleus is termed layering, coating or
‘‘onion-skin’’ growth mechanism. Another
mechanism is an agglomeration or coalescence
process that occurs upon particle collision. Whereas
growth by agglomeration mostly occurs when a
binder is added, layered growth is the result of
particle coating by the feed material, followed by
solidification of the material on the particle surface
(
Degreve et al., 2006).
The granulation regime depends on some factors
such as slurry viscosity and purity, N:P mole ratio,
granule curtain density, temperature of slurry and
seed to be coated, granule density, air temperature
inside the granulator-dryer, etc. Some of these
parameters can be observed and controlled, some of
them are not.
The design and control scheme of the drum
granulator-dryer normally force layered growth or
coating and block coalescence or agglomeration.
Sometimes the formation of undesirable
agglomerates indicates a shift of granulation regime
from layering to coalescence, which is not a normal
case of operation and must be avoided.
Granule growth by spraying the slurry onto the
previously formed seed is shown in Figure 3.
Initial seed dispersed slurry granule with added layer
Figure 3: Granule growth by layering.
To model the layering phenomenon, the
thickness of a new layer applied is determined by the
diameter of the initial particle and the volume of the
slurry applied. Assuming a spherical primary
particle and a uniform distribution of all sprayed
slurry applied onto the particle, the volume of the
added layer V
l
is calculated from the difference in
the volumes of the layered particle and the initial
one:
The thickness of the applied layer:
23
3
00
11
(6)
22
l
adVd
ππ
π
=+−
(1)
here d
0
– initial width of granule (seed), a – thickness of
the applied layer.
The explicit mass and energy balance model with
its wide and quite complex mathematical and
physical features is beyond the scope of this paper.
Hence, the following is the simplified version of the
model developed.
The overall mass balance inside the granulator in
liquid phase:
,,
L
L
in L out e c
dM
F
FFm
dt
=
−−−
(2)
here M
L
– accumulated mass of liquid solution, F
L,in
– flow
of liquid solution into the granulator, F
L,out
– flow of liquid
solution out of the granulator, F
e
– flow of evaporated
liquid solution, m
c
– mass of crystallized solution (solid
material).
The overall mass balance inside the granulator in
solid phase:
,,
S
S in S out c g att
dM
F
Fmmm
dt
=− ++−
(3)
here M
S
– accumulated mass of solid material, F
S,in
– flow
of solids into the granulator, F
S,out
– flow of solids out of
the granulator, m
g
– mass due to growth, m
att
– mass due to
attrition.
The overall energy balance inside the granulator:
in f r e l out
dE
EEEEEE
dt
=++−−−
(4)
here E – overall energy, E
in
– energy provided into the
granulator, E
out
– energy removed from the granulator, E
f
–
energy due to gas furnace action, E
r
– energy of reaction
heat, E
e
– energy for moisture evaporation, E
l
– loss of
energy from the granulator to environment.
The model presented is placed in stochastic
background, which can better suit the growth
kinetics, heat and mass transfer phenomena that
actually happen in the real plant, with addition of
uncertainty and plant equipment properties.
This section has presented only a part of the
general model, which is in nature a grey box.
Complementary models from measured process data
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
100
have been also built and expert information used to
enrich the model presented.
3.2 Statistical Analysis for Modeling
Nowadays it is possible to measure, store and retrieve
process sensors’ data and afterwards perform
statistical analysis to “mine” some knowledge. For
this purpose, descriptive and inferential statistics need
to be used.
Taking different combinations of data sets of the
essential process variables, the following results have
been obtained:
(1) Scatter plots of the parameters.
(2) Reduced linear correlation matrix with
entries of defined correlation degree (used for fast
determination of parameter combinations which have
a strong linear correlation).
(3) Linear models of the first order polynomial
(application of stepwise regression, which is a
technique for choosing variables, i.e. terms, to include
in a multiple regression model).
(4) Residuals, confidence intervals of
parameters, t-statistic, p-value, R
2
calculated for the
generated linear models.
(5) Plots of cross-correlation function for
probable lead/lag determination.
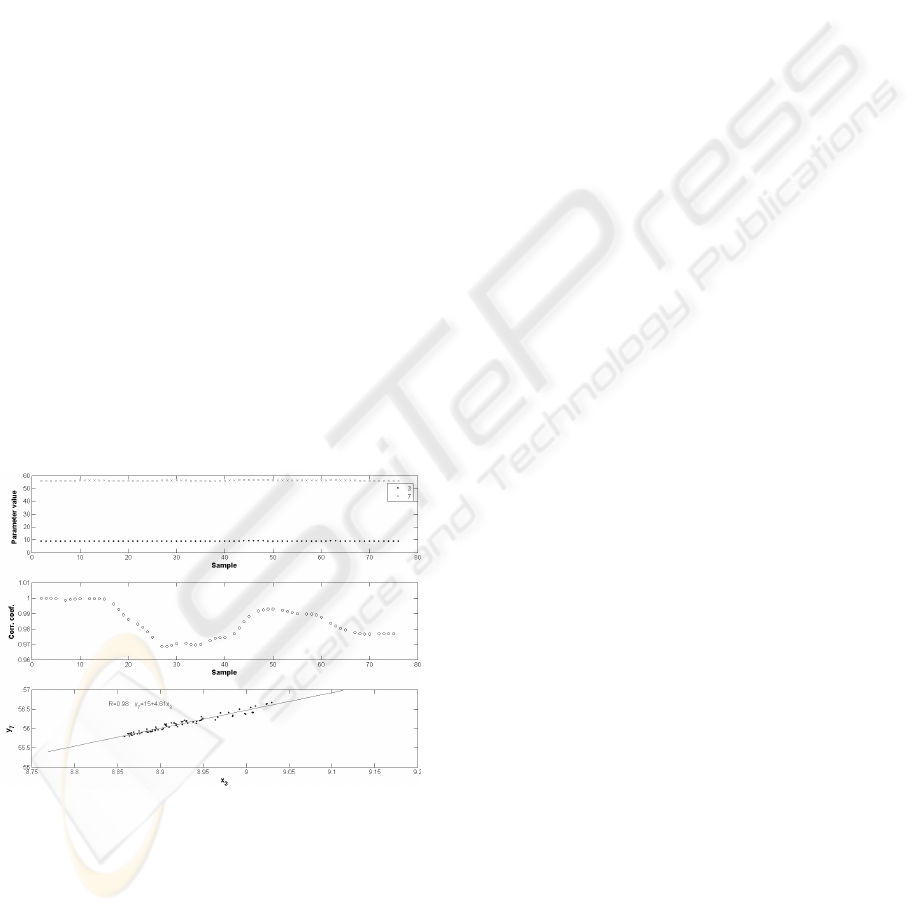
Figure 4 presents the fragment correlation and
regression analysis of two process parameters (
3 and
7).
Figure 4: Results of the regression analysis of process
parameters.
These findings are significant for determination
of process parameters and their relationship. They
can also provide additional knowledge for the plant
diagnostics. A more detailed statistical analysis of
granulation process can be found in (Valiulis and
Simutis, 2007).
Mere statistical analysis is rarely helpful. Some
heuristic knowledge should be also applied to make it
work.
3.3 Knowledge-based Modeling
Complex multiscale process systems which are
difficult to model properly (such as granulation)
require a combination of various analytical and
heuristic techniques. Effective solutions are often
based on information from heterogeneous
knowledge sources. One of them is knowledge-
based systems built on the methods and techniques
of Artificial Intelligence.
The expert knowledge of the process is an
invaluable source of knowledge, especially, when
there is a lack of reliable physical description and
suitable measurement equipment. Rule-based expert
systems use “if…then…” rules to represent human
expert knowledge, which is often a mix of
theoretical knowledge, heuristics derived from
experience, and special-purpose rules for dealing
with abnormal situations (Shang, 2004).
An example of the “if…then…” rule of new seed
formation inside the drum granulator-dryer is
presented as follows:
If
granule curtain in the spray zone is poor and
gas temperature in the spray zone is high, then new
small nuclei formation rate is high.
In the proposed modeling approach, the expert
knowledge is represented by the rule set. The rules
involve variables such as “poor”, “high”, dealing
with fuzziness, which is very common in real world
problems. Unlike conventional expert systems,
which are mainly symbolic reasoning engines, fuzzy
expert systems are oriented toward numerical
processing (Hemmer, 2008). These principles can be
applied for the future development of the granulation
process model and simulator for automated guidance
and diagnostic purposes.
4 SIMULATOR
Increasing capabilities of computer hardware and
software ensure the incorporation of complex
knowledge (models) represented by differential and
algebraic equations, measured process data, process
experts’ information, etc. But to be of use for the
day-to-day work of the engineer these models have
to become more user friendly, than the one that the
scientist is dealing with (Ihlow et al., 2004). A new
“GrowSim” simulation package for granulation
process modeling and simulation is under
MODELING OF CONTINUOUS FERTILIZER GRANULATION-DRYING CIRCUIT FOR COMPUTER
SIMULATION AND CONTROL PURPOSES
101

Figure 5: Graphical user interface of “GrowSim” simulator.
development to realize this concept. The simulator is
intended to be used by novice process operators to
improve their skills in process control and to acquire
knowledge of underlying mechanisms. The
graphical user interface (Figure 5) has been built to
mimic the process control environment available to
the process operator in the real plant, with important
additional information provided.
The simulation environment is composed of
sections where the operator can change the
manipulative process parameters, observe the
current or past output parameters, get some advice
on how the process in the current state should be
controlled by the skilled operator. The manual or
automatic process control modes are available. The
operator can take a challenge to manage the process
by hand or leave all or part of the job to PID or
Fuzzy controller. The simulation time is much
shorter compared to the real process and can be
easily adjusted if the computing resources are
sufficient. It is important to note that simulation can
be paused at any moment, to make it possible to
weigh one’s decisions. The main process parameters
are stored and can be observed during the simulation
or even later. The simulator is provided with routine
to compare the simulated and real measured process
data.
5 VALIDATION EXAMPLES
Some experiments have been carried out to validate
model performance against measured plant data in
prediction of the granule size distribution.
Experimental data have been obtained using particle
image analysis system.
Figure 6 presents the impact of slurry feed rate
on the cumulative granule size distribution.
In
phase A the process is kept in some steady
state, with the median granule size nearly 2.65 mm.
In
case B the slurry feed rate is increased
approximately by 35 %. In this situation the granule
median size is nearly 2.9 mm. Change in the slurry
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
102
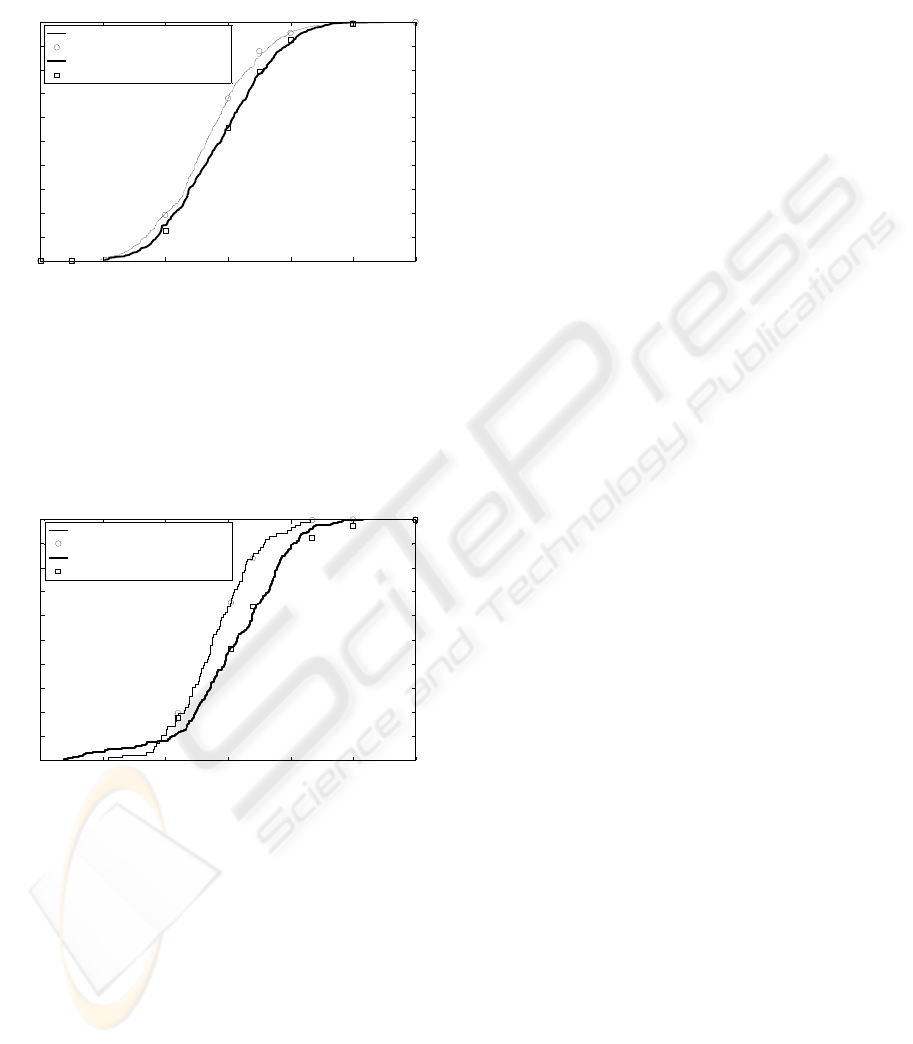
flow rate alters the granule growth rate. Increase in
the slurry flow rate raises the granule growth rate
and a shift of cumulative granule size distribution to
the right is observed.
0 1 2 3 4 5 6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Cumulative Size Distributions
Granule Diameter, mm
F(x)
Model Prediction (Slurry flow A)
Measured (Slurry flow A)
Model Prediction (Slurry flow B)
Measured (Slurry flow B)
Figure 6: Impact of the change of the slurry flow rate on
the cumulative granule size distribution.
Figure 7 presents the measured and simulated
cumulative granule size distributions of initial seeds
fed to the granulator (mean size is about 2.75 mm)
and granules flowing out of the granulator (mean
size is about 3.15 mm) in steady state.
0 1 2 3 4 5 6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Cumulative Size Distributions
Granule Diameter, mm
F(x)
Model Prediction (initial seeds)
Measured (initial seeds)
Model Prediction (granules out)
Measured (granules out)
Figure 7: Cumulative size distributions of initial seed flow
and granule flow out of the granulator.
6 CONCLUSIONS
An industrial DAP fertilizer granulation circuit,
including drum, sieves, crusher, transportation
system, has been modeled using basic physical
principles such as growth kinetics, mass and heat
transfer. Statistical analysis and system
identification procedures have been performed for
the estimation of unknown model parameters. As an
extension to the model, additional information has
been extracted from the process experts to define
unmeasured parameters and assess some equipment
properties. The whole model has been implemented
and simulation executed using “GrowSim” simulator
in the MATLAB environment.
Some model validation procedures have been
performed and the results appear to be in fair
accordance with the plant measured data. The
findings, presented in Figures 6 and 7, show some
kind of mismatch, but still can be treated
satisfactory.
The current and future research is focused on
further model development, implementation and
testing of different plant control modes such as PID,
Fuzzy and model predictive control. The primary
results demonstrate the need of combination of the
aforementioned control methods for a robust process
control.
REFERENCES
Degreve J., Baeyens J., Van de Velden M., De Laet S.
(2006). Spray-agglomeration of NPK-fertilizer in a
rotating drum granulator. Powder Technology, vol.
163, p. 176-183.
Findlay W.P., Peck G.R., Morris K.R. (2005).
Determination of Fluidized Bed Granulation End Point
Using Near-Infrared Spectroscopy and
Phenomenological Analysis. Journal of
Pharmaceutical Sciences, vol. 94, p. 604-612.
Hemmer M.C (2008). Expert Systems in Chemistry
Research. CRC Press.
Ihlow M., Drechsler J., Peglow M., Henneberg M.,
Mörl L. (2004). A New Comprehensive Model and
Simulation Package for Fluidized Bed Spray
Granulation Processes. Chemical Engineering and
Technology, vol. 27, p. 1139-1143.
Salmon A.D., Hounslow M.J., Seville J.P.K. (2007).
Handbook of Powder Technology, vol. 11.
Granulation. Elsevier.
Shang Yi (2004). Expert Systems. The Electrical
Engineering Handbook (Section 5). Elsevier Academic
Press, p. 367-377.
Valiulis G., Simutis R. (2007). Application of Regression
Analysis for Modelling of Granule Size Distribution.
Proceedings of International Conference “Electrical
and Control Technologies – 2007”, p. 62-67.
Wang F.Y, Cameron I.T., (2002). Review and future
directions in the modelling and control of continuous
drum granulation. Powder Technology, vol. 124, p.
238-253.
MODELING OF CONTINUOUS FERTILIZER GRANULATION-DRYING CIRCUIT FOR COMPUTER
SIMULATION AND CONTROL PURPOSES
103
