A COMPARATIVE STUDY BETWEEN CONVENTIONAL AND

CONTINUOUS GENETIC ALGORITHMS FOR THE SOLUTION

OF CARTESIAN PATH GENERATION PROBLEMS OF ROBOT

MANIPULATORS

Za'er Salim Abo-Hammour, Mohammad Suleiman Saraireh

Jordan University, Faculty of Engineering, Mechatronics Department, Amman-Jordan

Mutah University, Faculty of Engineering, Computer Engineering Department, Mutah-Kerak-Jordan

Othman M-K. Alsmadi

Jordan University, Faculty of Engineering, Electrical Department, Amman-Jordan

Keywords: Robot manipulators, Singularity avoidance, Cartesian path generation, Inverse kinematics problem,

Continuous genetic algorithms, Conventional genetic algorithms.

Abstract: In this paper, a comparative study between the continuous and the conventional GAs for the solution of

Cartesian path generation problems of robot manipulators is performed. The difference between both

algorithms lies in the ways in which initialization phase, the crossover operator, and the mutation operator

are applied. Generally, the operators of the Continuous Genetic Algorithms (CGA) are of global nature, i.e.,

applied at the joint’s path level, while those of conventional GA are of local nature, i.e., applied at the path

point level. It was concluded from the simulations included that CGAs have several advantages over

conventional GAs when applied to the path generation problems; first, the joints’ paths obtained using the

conventional GA are found to be of highly oscillatory nature resulting in very large net joints displacements

consuming more energy and requiring more time. This problem is totally avoided in CGA where the

resulting joints’ paths are smooth. Second, the CGA has faster convergence speed (number of generations

required for convergence) than the conventional GA. Third, the average execution time per generation in the

conventional GA is two to three times that in the CGA. This is due to the fact that the conventional GA

requires a coding process, which is not the case in the CGA. Fourth, the memory requirements of the

conventional GA are higher than those of the CGA because the former uses genotype and phenotype

representations while the later utilizes only the phenotype representation.

1 INTRODUCTION

Genetic algorithms, GAs, are broadly applicable,

general-purpose, generate-and-test optimization

methods based on Darwinian principles of biological

evolution, that is, "the survival of the fittest" and the

genetic operators. They were developed by Holland

(Holland, 1975) to study the adaptive process of

natural systems and to develop artificial systems that

mimic the adaptive mechanism of natural systems.

Conventional genetic algorithms were used by

the robotics community for solving the path

generation problems of robot manipulators where

the inverse kinematics problem is formulated as an

optimization problem and is then solved using GAs

based on the use of the forward kinematics model of

the manipulator. In this regard, Parker et. al.1989

introduced genetic algorithms for solving the inverse

kinematics problem of redundant manipulators

where GAs were used to move a robot to a target

location while minimizing the largest joint

displacement from the initial position. After that,

Davidor proposed a special GA for path generation

problem of redundant manipulators (Davidor, 1991).

He considered generating robot path as a typical

ordered-dependent process and presented a GA

model for this problem. The main characteristics of

his algorithm are the use of dynamic individuals

417

Salim Abo-Hammour Z., Suleiman Saraireh M. and M-K. Alsmadi O. (2009).

A COMPARATIVE STUDY BETWEEN CONVENTIONAL AND CONTINUOUS GENETIC ALGORITHMS FOR THE SOLUTION OF CARTESIAN PATH

GENERATION PROBLEMS OF ROBOT MANIPULATORS.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 417-424

DOI: 10.5220/0002206404170424

 SciTePress

structures and a modified crossover operator called

analogous crossover. The goal of the proposed GA is

to minimize the accumulative deviation between the

generated and the desired path.

CGA has been introduced recently as an

alternative and efficient technique for the solution of

path generation problems of robot manipulators

(Abo-Hammour et al, 2002). The CGA is that

algorithm which depends on the evolution of curves

in one-dimensional space. In general, CGAs use

smooth operators and avoid sharp jumps in the

parameter values. The algorithm was a contribution

to the solution of the inverse kinematics problem of

manipulators based on the concept of the

minimization of the accumulative path deviation.

The effect of various CGA operators and genetic-

related control parameters, and the effect of various

robot-related parameters on the convergence speed

of our proposed methodology for Cartesian path

generation was explored in (Abo-Hammour, 2005)

and (Abo-Hammour, 2002).

CGAs possess several advantages when applied

to path generation problems of robot manipulators

(Abo-Hammour et al, 2002): first, it can be applied

to any general serial manipulator with positional

degrees of freedom that might not have any derived

closed-form solution for its inverse kinematics.

Second, to the authors’ knowledge, it is the first

singularity-free path generation algorithm that can

be applied at the path update rate of the manipulator.

Third, extremely high accuracy can be achieved

along the generated path almost similar to analytical

solutions, if available. Fourth, the proposed

approach can be adopted to any general serial

manipulator including both non-redundant and

redundant systems.

In this paper, a detailed comparative study

between conventional and CGAs for the solution of

path generation problems of robot manipulators in a

free-of-obstacles workspace is performed. This

study includes the nature of the joints’ paths

obtained using both algorithms, the effect of the

joints’ limits on the solutions obtained using

conventional genetic algorithm, the influence of the

degree of redundancy and the number of knots along

the Cartesian path on the convergence speed of both

algorithms, and finally a step by step switching from

conventional genetic algorithm to CGA. It is to be

noted that both algorithms are based on the concept

of the minimization of the accumulative path

deviation only; no other objective functions are

included in this work.

The organization of the remainder of the paper is

as follows: the formulation of the path generation

problem for solution by genetic algorithms is

described in section 2. Section 3 covers both of the

CGA and the conventional genetic algorithm in

details. The comparative study between the two

algorithms is covered in Section 4. Finally,

conclusions are given in Section 5.

2 FORMULATION OF THE PATH

GENERATION PROBLEM

Let us consider a robot manipulator with M degrees

of freedom and N task space coordinates. Assume

that a desired Cartesian path, P

, is given, the

problem is to find the set of joint paths, P

, such that

the accumulative deviation between the generated

Cartesian path, P

, and the desired Cartesian path,

, is minimum. In other words, we are interested in

the determination of a set of feasible joint angles,

which corresponds to a set of desired spatial

coordinates of the end-effector in the task space.

It is to be noted that after the sampling process

by N

samples, P

and P

are matrices of dimension

N by N

while P

is a matrix of M by N

dimension.

After sampling the geometric path, at the path

update rate for best accuracy, the generated values of

the joint angles using the genetic algorithm, P

, are

used by the direct (forward) kinematics model of the

robot to obtain the generated Cartesian path given

by.

)(

PFP

kgc

(1)

Where F

represents the forward kinematics

model of the manipulator.

The deviation between the desired Cartesian

path, P

, and the generated Cartesian path, P

, at

some general path point, i, is given as.

∑

−=

gcdc

ikPikPiE

),(),()(

(2)

The accumulative deviation between the two

paths (desired and generated) depends on whether

the initial and final joint angles corresponding to the

initial and final configurations of the end-effector

are given in advance using the inverse kinematics

model of the manipulator or through other numerical

technique (fixed end points) or the case in which the

initial and final joint angles are not given (free end

points). For the fixed end points case, the

accumulative deviation between the two paths is

given by the formula.

∑∑∑

−

=−=

)(),(),(

gcdc

iEikPikPE

(3)

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

418

While for the free end points case, the accumulative

deviation between the two paths is given by the

formula.

∑∑∑

===

=−=

gcdc

)i(E)i,k(P)i,k(PE

(4)

The fitness function, a nonnegative measure of the

quality of individuals, is defined as:

(5)

The optimal solution of the problem is obtained

when the deviation function, E, approaches zero and

correspondingly the fitness function, F, approaches

unity.

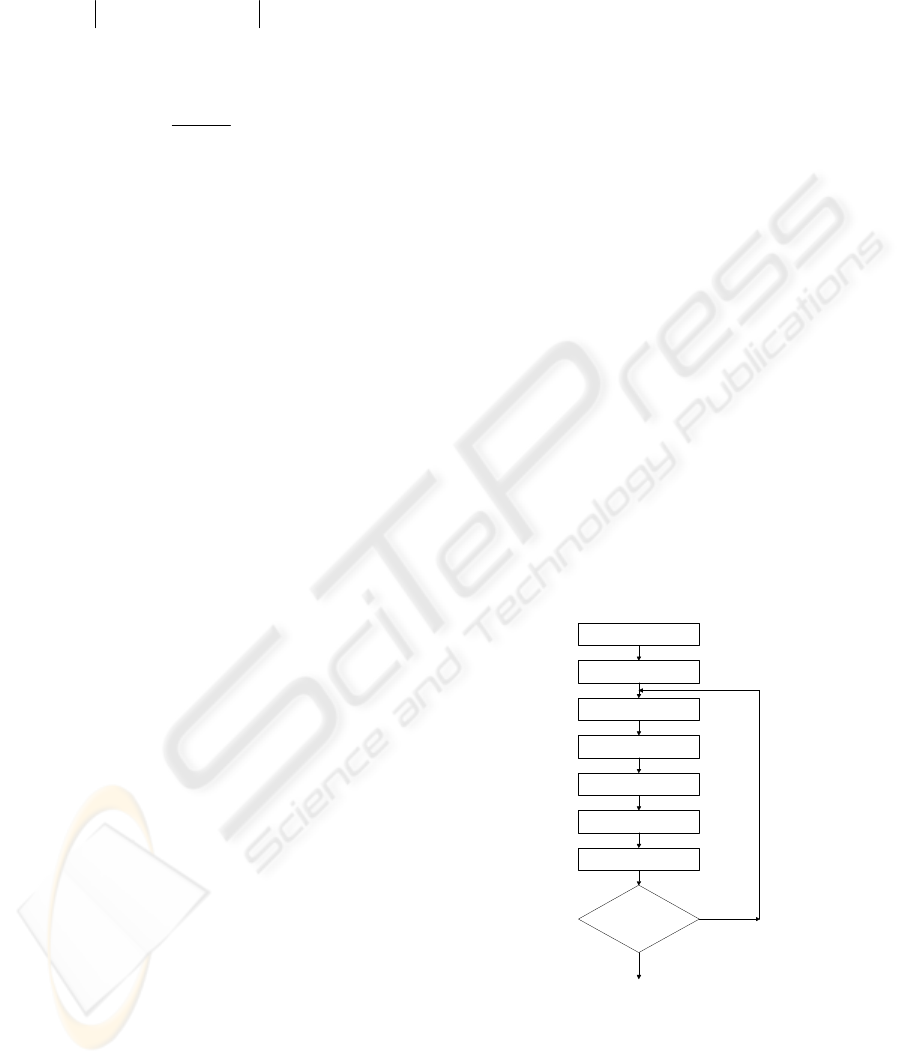
3 GENETIC ALGORITHMS

GAs are based on the triangle of genetic

reproduction, evaluation and selection (Goldberg,

1989). Genetic reproduction is performed by means

of two basic genetic operators: crossover and

mutation. Evaluation is performed by means of the

fitness function that depends on the specific

problem. Selection is the mechanism that selects

parent individuals with probability proportional to

their relative fitness. The genetic algorithm used in

this work consists of the following steps:

1. Initialization. An initial population comprising

of N

individuals is randomly generated in this

phase.

2. Evaluation. The fitness, a nonnegative measure

of quality used as a measure to reflect the

degree of goodness of the individual, is

calculated for each individual in the population

as given in Equation 6.

3. Selection. In the selection process, individuals

are chosen from the current population to enter

a mating pool devoted to the creation of new

individuals for the next generation such that the

chance of a given individual to be selected to

mate is proportional to its relative fitness. This

means that best individuals receive more copies

in subsequent generations so that their desirable

traits may be passed onto their offspring. This

step ensures that the overall quality of the

population increases from one generation to the

next.

4. Crossover. Crossover provides the means by

which valuable information is shared among the

population. It combines the features of two

parent individuals to form two children

individuals that may have new patterns

compared to those of their parents and plays a

central role in GAs.

5. Mutation. Mutation is often introduced to guard

against premature convergence. Generally, over

a period of several generations, the gene pool

tends to become more and more homogeneous.

The purpose of mutation is to introduce

occasional perturbations to the parameters to

maintain genetic diversity within the population.

6. Replacement. After generating the offspring’s

population through the application of the

genetic operators to the parents’ population, the

parents’ population is totally replaced by the

offspring’s population. This is known as non-

overlapping, generational, replacement. This

completes the “life cycle” of the population.

7. Termination. The GA is terminated when some

convergence criterion is met. Possible

convergence criteria are: the fitness of the best

individual so far found exceeds a threshold

value, the maximum number of generations is

reached, or the progress limit, the improvement

in the fitness value of the best member of the

population over a specified number of

generations is less than some predefined

threshold, is reached. After terminating the

algorithm, the optimal solution of the problem is

the best individual so far found. The block

diagram of the genetic algorithm is given in

Figure1.

TERM INATION

OF GA ?

YES

STOP

FITNESS EVALUATION

REPLACEMENT

CROSSOVER

MUTATION

SELECTION

FITNESS EVALUATION

INITIALIZATION

Figure 1: Block Diagram of the Genetic Algorithm.

The conventional genetic algorithm and the CGA

used in our work consist of the steps given

previously. The evaluation step, selection step,

replacement step and the termination step are

identical in both algorithms. The differences

A COMPARATIVE STUDY BETWEEN CONVENTIONAL AND CONTINUOUS GENETIC ALGORITHMS FOR

THE SOLUTION OF CARTESIAN PATH GENERATION PROBLEMS OF ROBOT MANIPULATORS

419

between both algorithms lie in the initialization

phase, the crossover operator, and the mutation

operator. These operators have the same goal in both

algorithms; the difference lies in the way in which

each operator is applied in the corresponding

algorithm. These operators are applied at the joint’s

path level in case of the CGA while they are applied

at the path point level in case of conventional

genetic algorithm. That is, the operators of the CGA

are of global nature while those of conventional

genetic algorithm are of local nature. In addition to

that, it is to be noted that the conventional genetic

algorithm uses the genotype and phenotype data

presentations while the CGA uses only the

phenotype data presentation. This fact requires a

coding process in conventional genetic algorithm,

which is not the case in CGA. The CGA is fully

described in (Abo-Hammour et al, 2002). The reader

is kindly asked to read this reference for the

complete details about it.

The operators of the conventional genetic

algorithm that include the initialization phase, the

crossover operator, and the mutation operator are

applied at the path point level. In relation to the

initialization phase, individuals are generated

randomly at the gene level. Conventional crossover

involves exchanging genes between each pair of

parents selected from mating pool. It is generally

applied with relatively high probability of crossover,

. Regarding the mutation operator, the bitwise

complement mutation is applied in the conventional

genetic algorithm at the gene level with some low

probability of mutation, P

. It is realized by

performing bit inversion (flipping) on some

randomly selected bit positions of children bit

strings.

To summarize the evolution process in

conventional genetic algorithm, an individual is a

candidate solution of the joints’ angles; that is, each

individual consists of a string of L=M* N

* N

genes. Initially, N

individuals are randomly

generated representing the initial population. The

population undergoes the selection process, which

results in a mating pool among which pairs of

individuals are crossed with probability P

. This

process results in an offspring’s generation where

every individual child undergoes mutation with

probability P

. After that, the next generation is

produced according to the replacement strategy

applied. This process is repeated till the convergence

criterion is met where the M

parameters of the

best individual are the required joints’ angles.

4 SIMULATION RESULTS

The CGA and the conventional genetic algorithm

were used to solve the Cartesian path generation

problem of 2R and 3R planar manipulators. The

initial settings of the CGA parameters are as

follows: the population size is set to 500 individuals.

The rank-based selection strategy is used where the

rank-based ratio is set to 0.1. The individual

crossover probability is kept at 0.9; the joint

crossover probability is also set to 0.9. The

individual mutation probability and the joint

mutation probability are kept at 0.9. Generational

replacement scheme is applied where the number of

elite parents that are passed to the next generation is

one-tenth of the population. The genetic algorithm is

stopped when one of the following conditions is met.

First, the fitness of the best individual of the

population reaches a value of 0.99; that is the

accumulative deviation of the end-effector, E, of the

best individual is less than or equal to 0.01. Second,

the maximum deviation at any path point of the best

individual is less than or equal to 0.001. Third, a

maximum number of 10000 generations is reached.

Fourth, the improvement in the fitness value of the

best individual in the population over 1000

generations is less than 0.01. It is to be noted that the

first two conditions indicate to a successful

termination process (optimal solution is found),

while the last two conditions point to a partially

successful end depending on the fitness of the best

individual in the population (near-optimal solution is

reached).

The initial settings of the conventional genetic

algorithm parameters are similar to those of the

CGA except those related to crossover, mutation and

coding process which are as following: the crossover

probability is kept at 0.7, the mutation probability is

kept at 0.01. The uniform crossover method is used

as the algorithm’s default crossover method. The

required accuracy of the phenotype values is set to

0.001 and binary coding scheme is used.

Due to the stochastic nature of GAs, twelve

different runs were made for every result obtained in

this work using a different random number generator

seed; results are the average values whenever

possible.

The selected Cartesian path generation problem

is of straight line shape as given by:

25.0x,0.0x

finalinitial

)1i(*

x)i(X)i,1(P

initialfinal

initialdcdc

−

+==

(6)

kdcdc

NiiYiP ≤≤

1,25.0)(),2(

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

420

Two manipulators are used in this work; 2R

planar manipulator and 3R planar redundant

manipulator. For the 2R manipulator, the link

parameters are L

=L=0.5 meter. For this case,

N=2, M=2,

lower

(h) =-180

and

upper

(h) =180

for

h=1,2. For the 3R planar redundant manipulator, the

link parameters are L

=0.5 meter. For this

case, N=2, M=3,

lower

(h) =-180

and

upper

(h)

=180

for h=1,2,3.

The number of path points along the Cartesian

path, N

, is set to 20 points. The initial and final

joints’ angles corresponding to the initial and final

configurations of the end-effector along the

Cartesian path are not given (i.e., free end points

case).

Initially, the conventional genetic algorithm was

used to solve the given path generation problem for

both manipulators. For the 2R manipulator, the

algorithm reaches a fitness value of 0.99 within 50

generations and the average path point deviation is

almost 0.0005 meter. The joints’ paths for the first

and second joints of the 2R manipulator are shown

in Figure 2.

2 4 6 8 10 12 14 16 18 20

-40

-20

100

120

140

160

Joint Angle (Degree)

Pat h Point (i)

2 4 6 8 10 12 14 16 18 20

-180

-135

-90

-45

135

180

Joint Angle (Degree)

Pat h Point (i)

(a) First Joint (b) Second Joint

Figure 2: Joints’ Paths of 2R Manipulator Using

Conventional Genetic Algorithm for (a) First Joint, and (b)

Second Joint.

It is obvious that the resulting solution curves in

joint space are highly oscillatory within the given

range of the joints’ limits. For the given

manipulator, there exist two possible solutions for

the inverse kinematics problem corresponding to

“elbow up” and “elbow down” configurations. It is

clear that the resulting solutions for both joints have

multiple switching points between these two

possible solutions. The switching process from one

solution corresponding to one robot configuration to

another solution corresponding to other robot

configuration results in very large net joints

displacements consuming more energy and requiring

more time. As a result, while solving such problems,

the switching from “elbow up” configuration to the

“elbow down” configuration should not be allowed

despite the fact that it is still a solution to the

problem. Generally, the probability of switching

between different solutions increases as the number

of feasible solutions of the manipulator increases.

For the 3R planar redundant manipulator, the

algorithm reaches a fitness value of 0.99 within 72

generations and the average path point deviation is

almost 0.0005 meter. The joints’ paths for the first,

second and third joints of the 3R manipulator are

shown in Figure 3. It is obvious that the resulting

joints’ paths are highly oscillatory within the range

of the joints’ limits, which results in large net

displacements of the joints.

2 4 6 8 10 12 14 16 18 20

-180

-135

-90

-45

135

180

Joint Angle (Degree)

Pat h Point (i)

2 4 6 8 101214161820

-180

-135

-90

-45

135

180

Joint Angle (Degree)

Pat h Point ( i)

(a) First Joint (b) Second Joint

2 4 6 8 101214161820

-180

-135

-90

-45

135

180

Joint Angle (Degree)

Path Point (i)

Figure 3: Joints’ Paths of 3R Manipulator Using

Conventional Genetic Algorithm for (a) First Joint, (b)

Second Joint, and (c) Third Joint.

The oscillatory behavior of the joints’ paths

encountered in the conventional genetic algorithm is

actually due to the nature of the initialization phase,

crossover operator, and mutation operator used in

the algorithm. These three operators are applied at

the path point level in the conventional genetic

algorithm. Conventional initialization phase implies

that consecutive path points might have opposite

extreme values within the given range of the joint’s

limits. The problem of oscillatory values among

consecutive path points is emphasized when the

range of joint’s limits is extended as discussed

previously. This problem is bypassed in CGA by the

use of smooth curves in the initial population that

eliminate the possibility of highly oscillating values

among the consecutive path points.

Conventional crossover operator results in a

jump in the value of the parameter in which the

crossover point lies (discontinuity) while keeping

A COMPARATIVE STUDY BETWEEN CONVENTIONAL AND CONTINUOUS GENETIC ALGORITHMS FOR

THE SOLUTION OF CARTESIAN PATH GENERATION PROBLEMS OF ROBOT MANIPULATORS

421

Table 1: Step-by-Step Switching to CGA for the 2R Manipulator.

Initialization

Type

Crossover Type Mutation Type

Avg. Execution

Time (Seconds)

Avg. No of

Generations

Avg. No. of

Switchings

Conventional Conventional Conventional 143.99 54 9

Conventional Conventional Continuous 160.59 57 7

Conventional Continuous Conventional 221.2 78 7

Conventional Continuous Continuous 261.44 100 2

Continuous Conventional Conventional 117.37 48 1

Continuous Conventional Continuous 109.97 49 0

Continuous Continuous Conventional 119.09 55 0

Continuous Continuous Continuous 99.11 47 0

Table 2: Step-by-Step Switching to CGA for the 3R Manipulator.

Initialization

Type

Crossover

Type

Mutation

Type

Avg. Execution

Time (Seconds)

Avg. No. of

Generations

Nature of Joints’ Paths

Conventional Conventional Conventional 487.72 124

Oscillations With Large

Magnitude

Conventional Conventional Continuous 390.06 105

Oscillations With Medium

Magnitude

Conventional Continuous Conventional 295.14 83

Oscillations With Large

Magnitude

Conventional Continuous Continuous 486.1 144

Oscillations With Medium

Magnitude

Continuous Conventional Conventional 188.89 53

Oscillations With Small

Magnitude

Continuous Conventional Continuous 191.2 56

Oscillations With Small

Magnitude

Continuous Continuous Conventional 181.57 55

Oscillations With Small

Magnitude

Continuous Continuous Continuous 148.85 49 Smooth Solution Curves

the other parameters the same or exchanged between

the two parents. It is clear that each crossing point

results in a discontinuity in the joint angles of the

obtained children. The worst case obtained regarding

the discontinuity of the resulting curves of the

children happens in the uniform crossover process.

In this scheme, the smoothness of the joint’s paths of

the parents is completely spoiled since crossover

happens at every path point. The solution to the non-

smoothness of the resulting joint’s paths is through

the use of the tangent hyperbolic crossover function

used in CGA that results in smooth transition in the

joint values of the two parents while generating the

two children.

Conventional mutation process changes only the

value of the joint angle of the path point in which

mutation occurs while keeping other joint angles in

the joint’s path unchanged. This process results in a

jump in the value of the joint angle in which

mutation takes place and the overall path will

become of oscillatory behavior. The discontinuity in

the joint’s path depends on the number of mutations

that take place in the path and the position of the bit

at which mutation takes place; that is, if the mutation

bit is leftmost, then the discontinuity will be larger

than that of rightmost mutation bit. This problem is

solved in CGA by applying the Gaussian mutation

function that is of global nature. In our approach,

mutation is applied at the joint’s path level rather

than path point level. As a result, mutation function

will start from zero values and increases/decreases

slowly till the peak then it will go back to zero

values at the other end.

After that, the effect of both versions

(conventional and continuous) of the initialization

phase, crossover operator and mutation operator on

the nature of the joints’ paths obtained and the

convergence speed of the hybrid algorithm is

studied. Table 1 gives the relevant data for the 2R

manipulator while Table 2 gives the relevant data for

the 3R manipulator. From Table 1, it is clear that the

maximum number of switching between the two

existing solutions of the inverse kinematics problem

for the 2R manipulator happens in case of the

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

422

conventional genetic algorithm (i.e., conventional

types of initialization, crossover and mutation).

Furthermore, the initialization phase has the greatest

effect on the smoothness/non-smoothness of the

solution curves; that is, in case of conventional

initialization, the number of switching points is 6 on

average while in case of continuous initialization,

the number of switching points is 0 on average. It is

also clear that as the number of conventional

processes decreases, the number of switching points

decreases. The minimum execution time and the best

convergence speed are achieved using the CGA (i.e.,

continuous types of initialization, crossover and

mutation). Regarding the 3R manipulator, it is clear

that the initialization phase has the greatest effect on

the smoothness/non-smoothness of the solution

curves; that is, in case of conventional initialization,

the joints’ paths are of oscillatory nature with large

or medium magnitude oscillations while in case of

continuous initialization, the joints’ paths are either

smooth or of oscillatory nature with small magnitude

oscillations. The minimum execution time and the

best convergence speed are achieved using the CGA

(i.e., continuous types of initialization, crossover and

mutation). For both manipulators, the conventional

initialization, continuous crossover and continuous

mutation case results in the largest number of

generations required for convergence. Regarding the

case in which the conventional initialization,

continuous crossover and conventional mutation are

used which is almost similar to the algorithm

proposed by Davidor, it is observed that this hybrid

scheme still results in oscillations with large

magnitude as shown in Table 2. This is an expected

result since the smoothness achieved by the

continuous crossover process is disturbed by the

conventional mutation process. This goes in

agreement with our previous comments about his

algorithm that even after the application of the

analogous crossover operator, the oscillatory

behavior of the joints’ paths is not totally avoided

due the discontinuities, which might appear in the

initialization phase and due to the mutation operator.

The joints’ paths for the first and second joints of

the 2R manipulator using CGA are shown in Figure

4. It is obvious that the resulting solution curves in

joint space are smooth and do not have any

switching between the two possible solutions, which

results in minimizing the net displacement of the

joints. The joints’ paths for the first, second and

third joints of the 3R manipulator are shown in

Figure 5 where similar observations are concluded

regarding the smoothness of the solution curves.

2 4 6 8 101214161820

-25

-20

-15

-10

-5

Joint Angle (Degree)

Path Poi nt ( i)

2 4 6 8 10 12 14 16 18 20

136

138

140

142

144

146

148

150

152

Joint Angle (Degree)

Pat h Point (i)

(a) First Joint (b) Second Joint

Figure 4: Joints’ Paths of 2R Manipulator Using CGA for

(a) First Joint, and (b) Second Joint.

2 4 6 8 10 12 14 16 18 20

-30

-25

-20

-15

-10

-5

Joint Angle (Degree)

Path Poi nt ( i)

2468101214161820

100

110

120

Joint Angle (Degree)

Pat h Point (i)

(a) First Joint (b) Second Joint

2468101214161820

100

105

110

115

120

125

130

135

Joint Angle (Degree)

Path Point (i)

Figure 5: Joints’ Paths of 3R Manipulator Using CGA for

(a) First Joint, (b) Second Joint, and (c) Third Joint.

5 CONCLUSIONS

In this work, both of the continuous and the

conventional genetic algorithms were used for the

solution of the Cartesian path generation problems

of robot manipulators.

It was noted that the resulting joints’ paths using

conventional genetic algorithm have multiple

switching points among the possible solutions of the

non-redundant manipulators while they are of highly

oscillatory nature for the redundant manipulators

resulting in very large net displacements of the joints

for both systems. This oscillatory behavior in

conventional genetic algorithm is actually due to the

nature of the initialization phase, crossover operator,

and mutation operator used in the algorithm. First,

the conventional initialization phase results in

consecutive path points that might have opposite

extreme values within the given range of the joints’

limits. Second, the conventional crossover operator

results in a jump in the value of the parameter in

A COMPARATIVE STUDY BETWEEN CONVENTIONAL AND CONTINUOUS GENETIC ALGORITHMS FOR

THE SOLUTION OF CARTESIAN PATH GENERATION PROBLEMS OF ROBOT MANIPULATORS

423

which the crossover point lies, while keeping the

other parameters the same or exchanged between the

two parents. Third, the conventional mutation

process changes only the value of the joint angle of

the path point in which the mutation occurs while

keeping other joint angles in the joint’s path

unchanged. The resulting discontinuity in the joint’s

path depends on the number of mutations that take

place in the path and the position of the bit at which

mutation takes place. These three operators are

designed in CGA such that they result in smooth

joints’ paths from one side and maintain an excellent

accuracy along the Cartesian path from the other

side. Among the three operators, it was noted that

the initialization phase has the greatest effect on the

smoothness/non-smoothness of the joints’ paths. The

convergence speed of the CGA in terms of both the

number of generations required for convergence and

the average execution time is much superior to that

of the conventional genetic algorithm.

REFERENCES

Abo-Hammour, Z., Mirza, N., Arif, M., 2002. Cartesian

Path Planning of Robot Manipulators Using

Continuous Genetic Algorithms. In Robotics and

Autonomous Systems; 41(4):179-223.

Abo-Hammour, Z., 2005. A Novel Continuous Genetic

Algorithms For the Solution of the Cartesian Path

Generation Problem of Robot Manipulators. In Robot

Manipulators.

Abo-Hammour, Z., 2002. Advanced continuous genetic

algorithms and their applications in the motion

planning of robotic manipulators and the numerical

solution of boundary value problems; Ph.D. thesis.

Davidor, Y., 1991. Genetic Algorithms and Robotics: A

Heuristic Strategy for Optimization, World Scientific.

Goldberg, D., 1989. Genetic Algorithms in Search,

Optimization, and Machine Learning, Addison -

Wesley, New York.

Holland, J., 1975. Adaptation in Natural and Artificial

Systems, University of Michigan Press, Ann Arbor.

Parker, J., Koogar, A., and Goldberg, D., 1989, Inverse

Kinematics of Redundant Robots Using Genetic

Algorithms, In IEEE Conference on Robotics and

Automation.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

424