TRANSITION VELOCITY FUNCTION

FOR IMPULSE CONTROL SYSTEMS

Stephen van Duin

, Matthias Ahlswede

and Christopher D. Cook

Faculty of Engineering, University of Wollongong, Northfields Avenue, Gwynnville, Australia

Institute of Production Engineering and Machine Tools, Leibniz University Hannover, Hannover, Germany

Keywords: Impulsive Control, Static Friction, Limit Cycle, Stick-slip, Impulse Shape, Friction Model, Accuracy.

Abstract: This paper presents a modified impulse controller that is used to improve the velocity tracking of a

servomechanism having characteristics of high nonlinear friction. A hybrid control scheme consisting of a

conventional PID part and an impulsive part is used as a basis to the modified controller. This has

previously been used to improve the position and velocity tracking of robot manipulators at very low

velocities. Experiments show that at higher velocities the improved performance of the impulse part of the

hybrid controller diminishes and can be counterproductive at these speeds when compared to conventional

PID control alone. The modified hybrid impulse controller in this paper uses a mathematical function to

transition the amount of torque from an impulse as a function of velocity to achieve more precise tracking

across a range of velocities.

1 INTRODUCTION

Precision robot manufacturers continually strive to

increase the accuracy of their machinery in order to

remain competitive. The ability of a robot

manipulator to position its tool centre point to within

a very high accuracy allows the robot to be used for

more precise tasks. For positioning of a tool centre

point, the mechanical axes of a robot will be

required to be precisely controlled around zero

velocity where friction is highly non-linear and

difficult to control. Furthermore, precise velocity

control at high velocities is typically required for

increased productivity. Each axis of a robot is

typically controlled by a servomechanism and this

paper deals with improving the control of these basic

robot components in the presence of friction.

Nonlinear friction is inherently present in all

mechanisms and can cause stick-slip during precise

positioning. In many instances, stick-slip has been

reduced or avoided by modifying the mechanical

properties of the system; however this approach may

not always be practical or cost effective.

Alternatively, advances in digital technology have

made it possible for the power electronics of

servomechanisms to be controlled with much greater

flexibility. By developing better controllers, the

unfavourable effects of non-linear friction may be

reduced or eliminated completely.

Impulse control has been successfully used for

accurate positioning of servomechanisms with high

friction where conventional control schemes alone

have difficulty in approaching zero steady state

error. Static and Coulomb friction can cause a

conventional PID controller having integral action

(I), to overshoot and limit cycle around the reference

position. This is particularly a problem near zero

velocities where friction is highly non linear and the

servomechanism is most likely to stick-slip. Despite

the above difficulties, PID controllers are still

widely used in manufacturing industries because of

their relative simplicity and reasonable robustness to

parameter uncertainty and unknown disturbances.

Stick-slip can be reduced or eliminated by using

impulsive control near or at zero velocities. The

impulsive controller is used to overcome static

friction by impacting the mechanism and moving it

by microscopic amounts. By combining the

impulsive controller and conventional controller the

PID part can be used to provide stability. Moving

towards the reference position the impulse controller

is used to improve accuracy for the final positioning

where the error signal is small.

213

van Duin S., Ahlswede M. and Cook C. (2009).

TRANSITION VELOCITY FUNCTION FOR IMPULSE CONTROL SYSTEMS .

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,

pages 213-221

DOI: 10.5220/0002207402130221

 SciTePress

By applying a short impulse of sufficient force,

plastic deformation occurs between the asperities of

mating surfaces resulting in permanent controlled

movement. If the initial pulse causes insufficient

movement, the impulsive controller produces

additional pulses until the position error is reduced

to a minimum.

A number of investigators have devised

impulsive controllers which achieve precise motion

in the presence of friction by controlling the height

or width of a pulse. Yang and Tomizuka (Yang et

al., 1988) applied a standard rectangular shaped

pulse in which the height of the pulse was a force 3

to 4 times greater than the static friction to guarantee

movement. The width of the pulse was adaptively

adjusted proportional to the error and was used to

control the amount of energy required to move the

mechanism towards the reference position.

Alternatively, Popovic (Popovic et al., 2000)

described a fuzzy logic pulse controller that

determined both the optimum pulse amplitude and

pulse width simultaneously using a set of

membership functions. Hojjat and Higuchi (Hojjat et

al., 1991) limited the pulse width to a fixed duration

of 1ms and varied the amplitude by applying a force

about 10 times the static friction.

In a survey of friction controllers by Armstrong-

Hélouvry (Armstrong- Hélouvry et al., 1994), it is

commented that underlying the functioning of these

impulsive controllers is the requirement for the

mechanism to be in the stuck or stationary position

before subsequent impulses are applied. Thus,

previous impulse controllers required each small

impacting pulse to be followed by an open loop slide

ending in a complete stop.

van Duin (van Duin et al., 2006), used a hybrid

PID + Impulsive controller to improve the precision

of a robot manipulator arm in the presence of static

and Coulomb friction. The design and functioning of

the controller does not require the mechanism to

come to rest between subsequent pulses, making it

suitable for both point-to-point positioning and

speed regulation. van Duin (van Duin et al., 2006)

manipulated the pulse shape to match the dynamic

friction by making this shape responsive to very

small changes in velocity.

The error in positioning during different tracking

tasks at zero and low velocities was greatly

improved. However, further experiments showed

that the PID + Impulse controller had greater errors

at high velocities compared to a simple PID

controller alone.

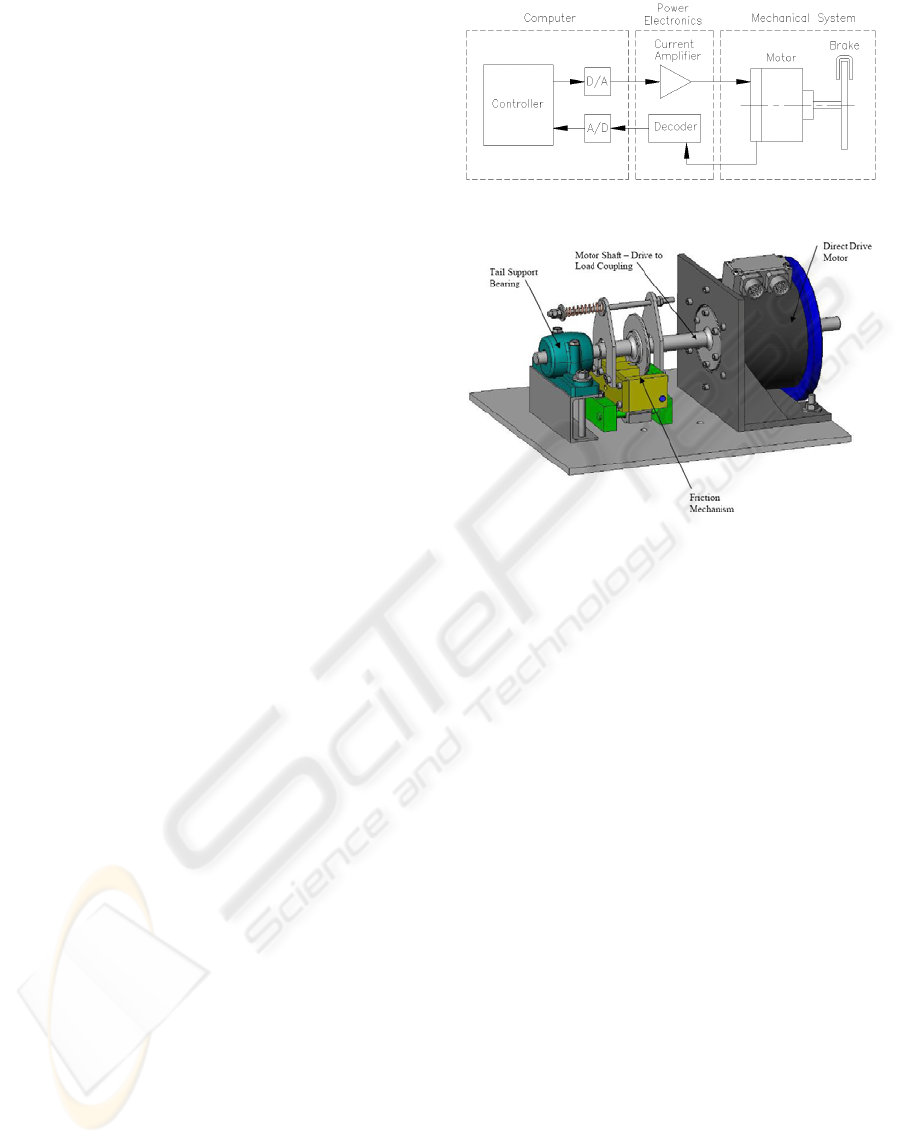
Figure 1: Experimental friction test bed.

Figure 2: Three dimensional drawing of the friction test

bed.

This paper presents a modified impulse

controller where the impulsive part of the hybrid

PID + Impulse controller is gradually disabled at

higher velocities so that the conventional linear PID

part is eventually solely providing the driving

torque. It is shown that at greater velocities, the

static and Coulomb friction is less influential and

that the system is more dominated by the relatively

linear viscous frictional effects. Using a transition

function the performance is shown to be improved

for both low and high velocities, while maintaining

system stability.

2 EXPERIMENTAL SYSTEM

2.1 Servomechanism

For these experiments a purpose built single axis

friction test-bed was used to simulate the conditions

typically observed in an industrial robot arm.

Figures 1 and 2 show the experimental friction

test bed system that consists of a single axis direct

drive servomechanism actuator coupled to a friction

generating disk brake. Torque is transmitted by the

actuator to the friction mechanism through a direct

coupled shaft to eliminate the presence of backlash,

gear cogging, belt cogging etc. Direct drive isolates

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

214

the friction characteristics; however, the impulse

control systems in this paper have been repeated on

a Hirata ARi350 SCARA robot with comparable

results.

Position data is obtained from a shaft encoder

housed within the motor and has a maximum

resolution of 2

counts per revolution or 1.198e-5

rad/count. Digital torque control of the motor is

achieved using a three phase direct drive servo

amplifier.

Matlab’s xPC target oriented server was used to

provide control to the servomechanism drive. For

these experiments the digital drive was used in

current control mode. This means the output voltage

from the 12-bit D/A converter gives a torque

command to the actuator’s power electronics, which

has a time constant of 0.1ms.

The system controller was compiled and run using

Matlab’s real time xPC Simulink® block code.

2.2 Hybrid PID + Impulse Controller

Figure 3 shows the block diagram of a PID linear

controller + impulsive controller. This hybrid

controller has been suggested by Li (Li et al., 1998)

where the PID driving torque and impulsive

controller driving torque are summed together. It is

unnecessary to stop at the end of each sampling

period; therefore, the controller can be used for both

position and speed control.

The controller can be divided into two parts; the

upper part is the continuous driving force for large

scale movement and control of external force

disturbances. The lower part is an additional

proportional controller k

pwm

with a pulse width

modulated sampled-data hold (PWMH), and is the

basis of the impulsive controller for the control of

stick-slip.

The system controller is sampled at 2 kHz. The

impulse itself is sampled and applied at one

twentieth of the overall sampling period (i.e. 100

Hz) to match the mechanical system dynamics.

Figure 4 shows a typical output of the hybrid

controller for one impulse sampling period

. The

pulse with a height f

is added to the PID output.

Because the PID controller is constantly active, the

system has the ability to counteract random

disturbances applied to the servomechanism. The

continuous part of the controller is tuned to react to

large errors and high velocity, while the impulse part

is optimized for final positioning where stiction is

most prevalent.

Figure 3: Block diagram of the experimental system

controller.

PID

Output

Figure 4: Friction controller output.

For large errors, the impulse width approaches

the full sample period

, and for very large errors, it

transforms into a continuous driving torque. When

this occurs, the combined control action of the PID

controller and the impulsive controller will be

continuous. Conversely, for small errors, the PID

output is too small to have any substantial effect on

the servomechanism dynamics.

The high impulse sampling rate, combined with a

small error, ensures that the integral (I) part of the

PID controller output has insufficient time to rise

and produce limit cycling. To counteract this loss of

driving torque, when the error is below a threshold,

the impulsive controller begins to segment into

individual pulses of varying width and becomes the

primary driving force. One way of achieving this is

to make the pulse width Δ determined by:

spwm

kek

)(

⋅

=Δ if |||)(|k

pwm p

fke ≤⋅

otherwise (1)

In (1)

()

fsignek=⋅

(2)

where e(k) is the error input to the controller, |f

| is a

fixed pulse height greater than the highest static

TRANSITION VELOCITY FUNCTION FOR IMPULSE CONTROL SYSTEMS

215

friction and

is the overall sampling period.

For the experimental results described in this

paper, the impulsive sampling period

was 10ms

and the pulse width could be incrementally varied by

1ms intervals. The pulse width gain k

pwm

, is

experimentally determined by matching the

mechanism’s observed displacement d to the

calculated pulse width t

using the equation of

motion:

()

pp C

ff f

−

, f

> 0 (3)

The gain is iteratively adjusted until the net

displacement for each incremental pulse width is as

small as practical.

To further improve the performance of the

controller, van Duin (van Duin et al., 2006) use a

modified impulse shape to better counteract the

dynamics of friction. To overcome stiction, it is

necessary to have an initial driving force greater

than the static friction. Immediately after motion

begins, the opposing friction reduces dramatically

and, if motion continues, will be maintained at the

Coulomb friction value. Figure 5 shows most of the

effective energy of the pulse commences

immediately after the static friction dissipates and

therefore the remaining pulse height after an initial

start-up pulse can be reduced much less than that

required to initiate motion.

This type of pulse was used for the experiments

in this paper.

Figure 5: Modified pulse with 2ms start up pulse to

overcome static friction and initiate motion.

2.3 Performance at Very Low to High

Velocity Regimes

This section investigates how the hybrid PID +

impulse controller performs at higher velocities

exceeding the Stribeck threshold of approximately

.09 rads. For this region of velocities, the highly non

linear static and negative viscous friction

components are substantially reduced relative to the

total and the Coulomb and viscous frictions become

the dominant resisting friction. For these velocities,

the conventional linear PID controller is well suited.

Subsequently, the addition of an impulse torque

request may be deleterious to the servomechanism’s

performance in the region of higher velocity.

Figure 6 shows a series of varying ramp

responses from 0.02 rad/s up to 0.35 rad/s using the

friction test bed. The range of speeds ensures that

the mechanism is operating in both the nonlinear and

linear friction regions. Figure 7 compares the Mean

Value of the Absolute Error (MAE) for each speed

from 7 to 10 seconds respectively. A standard form

for MAE is (Ogata, 1990):

()

∑

−=

MAE

(4)

Where n is the number of data points, x

is the

mechanism position, and x is the reference position.

Figure 6: Tracking response for the friction test bed using

PID and PID + impulse controllers for varying position

ramps (0.02 rad/s to 0.35 rad/s).

For the velocities below the Stribeck velocity

threshold, the hybrid PID + impulse controller

significantly outperforms the conventional PID

controller. However, as the velocity increases, the

mean errors of both the PID and PID + impulse

controllers begin to converge (ω≈0.15rad/s), and at a

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

216

critical velocity above the Stribeck region, the PID

controller becomes more precise. This increase in

precision for the PID controller can be expected

since for this higher range of velocities, a

conventional linear PID controller will sufficiently

counteract the linear fiction without the need of any

additional torque. These experiments show that

combining the impulse action for high range

velocities can be unnecessary and in some instances

counterproductive. One way to avoid this loss of

performance using a hybrid controller is to disable

the impulse torque request at higher velocities to

allow the PID part to work autonomously.

Figure 7: Mean value of the absolute error for each of the

position tracking ramps shown in Figure 6 for the period 7

– 10 seconds.

3 TRANSITION VELOCITY

CONTROLLER

This section evaluates a series of transition velocity

controller functions which disable or limit the

impulsive controller above the critical Stribeck

velocity.

3.1 On/Off Control using the Critical

Velocity

Here the controller’s impulsive part is switched off

at the critical velocity. The set of conditions for

which this occurs is simply defined by the

following:

≤)(vy critical velocity, then the impulse

force

= constant

(5)

Otherwise

zerof

Where y(v) is determined by differentiating the

mechanism’s actual position.

The initial assumption was that this action would

make the system unstable at this moment. Close

inspection of a velocity tracking task (Figure 8)

confirms the mechanism cyclically overshooting and

undershooting. This results in the error of the

position tracking task increasing for the critical

velocity and velocities nearby. This can be seen in

Figure 9 between the velocity range of 0.25 and 0.35

rad/s.

Figure 8: Velocity response when tracking defined

disabling velocity of v=0.25 rad/s.

Figure 9: Mean value of the absolute error of the

unmodified controllers and the modified PID plus Impulse

controller with a disabled impulsive part with respect to

the actual velocity.

The loss of torque from the impulsive controller

immediately affects the mechanism and the PID

controller cannot counteract this quickly enough.

The loss of torque causes the velocity to drop under

the critical velocity and the impulsive part is

immediately enabled again. This makes the system

unstable and the controller cyclically enables and

disables the impulse controller. However, at

velocities above this transition region the position

tracking error is consistent with the PID only

controller, as expected.

It is clear that using only servomechanism

velocity output as a function to control the transition,

cannot be an option if tracking accuracies near

critical velocities are to be maintained. A solution to

this is to transition the controller as a function of

TRANSITION VELOCITY FUNCTION FOR IMPULSE CONTROL SYSTEMS

217

reference velocity rather than system velocity as

shown in Figure 10.

Figure 10: Mean value of the absolute error of the

unmodified controllers and the modified PID plus Impulse

controller with a disabled impulsive part with respect to

the reference velocity.

3.2 Sinusoidal Reference Position

Tracking

To further trial the modified controller, an additional

experiment tested the system’s ability to track

changing velocities that pass through the critical

velocity regime. In this case, a sinusoidal position

reference ensures a continuous change in

velocities for both positive and negative

accelerations. By using the Integral Absolute Error

(IAE) criterion, the error of a statistically relevant

series of position trace experiments can be

calculated, and a performance measure between each

controller established. A standard measure is given

by (Ogata, 1990):

()et dt

∞

∫

(6)

Where e(t) is the error with respect to time t.

Figure 11: The IAE of the unmodified controllers and the

on/off modified controller.

Figure 11 shows a comparison of the results

where there is clearly no improvement in accuracy

for the modified PID + impulse controller over the

original hybrid controller for these conditions of

changing velocity. A subsequent breakdown of the

error with respect to time shows in Figure 12 that the

modified controller mostly counter-performs during

acceleration but also partly during deceleration.

Figure 12: The IAE of the unmodified controllers and the

on/off modified controller during (a) acceleration; and (b)

deceleration while tracking the sinusoidal position curve.

A closer examination of the position trace

(Figure 13) shows that the loss of torque during the

point of disabling creates a torque deficiency which

the conventional PID controller struggles to correct

in a reasonable time frame. A proposed solution to

this is to replace the instantaneous on/off switching

function with a linear decaying ramp so that abrupt

impulse torque removal is avoided and instead

gradually transitioned.

Figure 13: Comparison of the reference and actual position

during acceleration while tracking a sinusoidal position

input.

3.3 Transition Velocity Function

A solution to transitioning the impulse torque output

from unity gain to zero, is given by the following

simple linear function:

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

218

()yv a v b=⋅+ (7)

Where v is the reference velocity of the system

and the constants a and b are experimentally

determined by trial over a range of velocities either

side of the system’s critical velocity.

Figure 14: MAE for constant velocity position tracking

tasks for the unmodified and linear function transitional

impulse controllers.

Figure 14 compares the MAE for each controller.

Surprisingly, the linear transition function even

improves the accuracy in position at the intermediate

higher velocities before the impulse torque is fully

transitioned to zero. This improved performance

shows that the controller accuracy can be noticeably

improved by limiting the pulse height at higher

velocities instead of disabling it.

Subsequently, a new function with modified

requirements was determined. The function

provides:

• A fast reduction in pulse height matched to the

PID sampling rate when switching from full to

partial impulse control;

• Rather than disabling the full impulse

completely it instead reduces it to a fraction of

the original pulse height;

• Control over the magnitude of impulse for

either acceleration or deceleration regimes.

All of these requirements can be realised with an

exponential function. The basic equation used was:

cevy

bva

− )(

)( (8)

The parameter a was chosen to be -10 as the

exponential function should be designed to have a

negative slope that simultaneously reduces the

impulse height rapidly. The parameters b and c are

determined through boundary conditions as follows:

1)15.0(

)(10

=+==

−−

cevy

(9)

25.0)35.0(

)(10

=+==

−−

cevy

(10)

Solving these equations gives:

1326.0)(

)1358.0(10

−− v

evy (11)

Where v is the reference velocity given by the

tracking task. The boundary conditions are selected

by trial using a range of varying pulse heights.

Figure 15: Exponential function for transitioning the

limiting of the impulse torque with respect to velocity.

Figure 16: Typical controller torque command for a full

impulse and modified impulse applied to friction test bed.

Figure 17: MAE for constant velocity position tracking

tasks for the unmodified and transitional impulse

controllers.

Figure 15 shows a graphical representation of the

exponential function, while Figure 16 gives an

example of a typical controller torque command.

TRANSITION VELOCITY FUNCTION FOR IMPULSE CONTROL SYSTEMS

219

The exponential function was shown to provide a

significant improvement in the accuracy of velocity

tracking (Figure 17). However, further velocity

tracking experiments showed that the improvement

can only be achieved when tracking constant

velocities and is particularly counterproductive

during acceleration and varying deceleration. This is

caused by the insufficient response of the controller

to change the pulse height relative to the rapid

changes in velocity.

A solution for ensuring a smooth transition

between different tracking tasks with different pulse

heights is a time dependant exponential function

with additional conditions. If F

is the factor

determined by the modification done in the previous

section, the requirements for the new function are as

follows:

)0(

tf ==

(12)

1)(

∞=tf (13)

This leads to the following equation:

1)(

ln5.0

⎟

⎠

⎞

⎜

⎝

⎛

−+×−

etf

(14)

Multiplying this equation with Equation 11 gives

a smooth transition between the full impulse height

during the acceleration and the fraction of the pulse

height during constant velocity after acceleration.

To compare each controller for a range of conditions

and to test the controller’s stability, a varying

position tracking experiment was devised with the

resulting trace shown in Figure 18. This trajectory

was chosen as a demanding trajectory including

several velocity reversals and various velocity

gradients.

Figure 18: Position tracking task for testing stability.

After repeating the experiments for each

controller, the IAE criterion was used to compare

each controller and the results shown in Figure 19.

The results clearly show a marked improvement in

the overall accuracy of the system when using the

impulse controller with a time varying exponential

function to transition the impulse torque during

acceleration and deceleration. Furthermore, the

results show that the controllers are robust enough to

remain stable over the fairly demanding range of

reference conditions tested.

Figure 19: The IAE for the velocity tracking using the

unmodified controller, exponential function and

exponential function with time varying transition.

3.4 Discussion of Results

This set of results demonstrates the impulse

transitional velocity function can be successfully

applied to a servomechanism, having characteristics

of high non-linear friction. The results show that the

unmodified impulse controller significantly

outperforms the conventional PID controller at very

low velocities. However, as the velocity increases,

the mean errors of both the PID and PID + impulse

controllers begin to converge above the Stribeck

region and the PID controller becomes more precise.

By applying an exponential function which

includes consideration of time dependent boundary

conditions, the impulse controller can be

transitionally reduced to exploit the robustness of a

conventional PID controller at higher velocities

where viscous friction dominates.

A comparison of the Mean Value of the Absolute

Error and the Integral of the Absolute Error for each

controller shows that the impulse controller with the

velocity dependant exponential function for impulse

torque transitioning achieved a more precise result.

This controller was proven to be robust enough to

maintain stability during a rigorous position tracking

task.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

220

4 CONCLUSIONS

Advances in digital control have allowed the power

electronics of servo amplifiers to be manipulated in

a way that will improve servomechanism precision

without modification to the mechanical plant.

A previously developed hybrid PID + Impulse

controller which does not require the mechanism to

come to a complete stop between pulses has been

modified to further improve accuracy in the presence

of stick-slip friction. This modification transitions

the decay of the impulse torque command at higher

velocities. Many experimental tests showed that this

innovation provided substantial additional

improvement in the mechanism’s position accuracy

in comparison with other control strategies. This has

been demonstrated on a servomechanism which is

typical of those used to control each axis of

industrial mechanisms such as a robot arm.

Future work is proceeding on optimising the

parameters using a method generic to any

mechanism, which does not rely on trial and error

and is applicable to a greater rang of trajectories.

REFERENCES

Armstrong-Hélouvry, B., 1991, “Control of Machines with

Friction” Kluwer Academic Publishers, 1991, Norwell

MA.

Armstrong-Hélouvry, B., Dupont, P., and Canudas de

Wit, C., 1994, “A survey of models, analysis tools and

compensation methods for the control of machines

with friction” Automatica, vol. 30(7), pp. 1083-1138.

Canudas de Wit, C., Olsson, H., Åström, K. J., 1995 ”A

new model for control of systems with friction” IEEE

Tansactions on Automatic Control, vol. 40 (3), pp.

419-425.

Dahl, P., 1968, “A solid friction model” Aerospace Corp.,

El Segundo, CA, Tech. Rep. TOR-0158(3107-18)-1.

Dahl, P, 1977, “Measurement of solid friction parameters

of ball bearings” Proc. of 6

annual Symp. on

Incremental Motion, Control Systems and Devices,

University of Illinois, ILO.

Hojjat, Y., and Higuchi, T., 1991 “Application of

electromagnetic impulsive force to precise

positioning” Int J. Japan Soc. Precision Engineering,

vol. 25 (1), pp. 39-44.

Johannes, V. I.., Green, M.A., and Brockley,C.A., 1973,

“The role of the rate of application of the tangential

force in determining the static friction coefficient”,

Wear, vol. 24, pp. 381-385.

Johnson, K.L., 1987, “Contact Mechanics” Cambridge

University Press, Cambridge.

Kato, S., Yamaguchi, K. and Matsubayashi, T., 1972,

“Some considerations of characteristics of static

friction of machine tool slideway” J. o Lubrication

Technology, vol. 94 (3), pp. 234-247.

Li, Z, and Cook, C.D., 1998, ”A PID controller for

Machines with Friction” Proc. Pacific Conference on

Manufacturing, Brisbane, Australia, 18-20

August,

1998, pp. 401-406.

Ogata, K., Modern Control Engineering. 1990,

Englewood Cliffs, New Jersey: Prentice Hall.

Olsson, H., 1996, “Control Systems with Friction”

Department of Automatic Control, Lund University,

pp.46-48.

Popovic, M.R., Gorinevsky, D.M., Goldenberg, A.A.,

2000, “High precision positioning of a mechanism

with non linear friction using a fuzzy logic pulse

controller” IEEE Transactions on Control Systems

Technology, vol. 8 (1) pp. 151-158.

Rabinowicz, E., 1958, “The intrinsic variables affecting

the stick-slip process,” Proc. Physical Society of

London, vol. 71 (4), pp.668-675.

Richardson, R. S. H., and Nolle, H., 1976, “Surface

friction under time dependant loads” Wear, vol. 37

(1), pp.87-101.

van Duin, S., 2006, “Impulse Control Systems for

Servomechanisms with Nonlinear Friction”, Ph.D.

dissertation, University of Wollongong.

van Duin, S, Cook, C., Li, Z., Alici, G., 2007, “A modified

impulse controller for Improved Accuracy of Robots

with Friction”, Proceedings International Conference

on Informatics in Control, Automation and Robotics,

Angers, France.

Yang, S., Tomizuka, M., 1988, “Adaptive pulse width

control for precise positioning under the influence of

stiction and Coulomb friction” ASME J .od Dynamic

Systems, Measurement and Control, vol. 110 (3), pp.

221-227.

TRANSITION VELOCITY FUNCTION FOR IMPULSE CONTROL SYSTEMS

221