
REAL-CODED GENETIC ALGORITHM IDENTIFICATION
OF A FLEXIBLE PLATE SYSTEM
S. Md Salleh, M. O. Tokhi and S. F.Toha
Dept.of Automatic Control and System Eng., University of Sheffield, Sheffield, U.K.
Keywords: Real-coded genetic algorithm, Parametric modelling, Flexible plate.
Abstract: Parametric modelling deals with determination of model parameters of a system. Parametric modelling of
systems may benefit from advantages of real coded genetic algorithms (RCGAs), as they do not suffer from
loss of precision during the processes of encoding and decoding compared with Binary Coded Genetic
Algorithm. In this paper, RCGA is used to identify the best model order and associated parameters
characterising a thin plate system. The performance of the approach is assessed on basis mean-squared
error, time and frequency domain response of the developed model in characterising the system. A
comparative assessment of the approach with binary coded GA is also provided. Simulation results signify
the advantages of RCGA over two further algorithms in modelling the plate system are also provided.
1 INTRODUCTION
Parametric modelling is defined as the process of
estimating parameters of a model characterising a
plant. The technique basically searches for
numerical values of the parameters so that to give
the best agreement between the predicted (model)
output and the measured (plant) output. Parametric
modelling can include both the parameter estimates
and the model structure. Statistical validation
procedures, based on correlation analysis, are
utilised to validate parametric models.
Several advantages motivating research intention
in a flexible structure are due to light weight, lower
energy consumption, smaller actuator requirement,
low rigidity requirement and less bulky design.
These advantages lead to extensive usage of flexible
plates in various applications such as space vehicles,
automotive industries, and the construction industry.
Modelling is the first step in a model-based control
development of a system. Accordingly, the accuracy
of the model is crucial for the desired performance
of the control system.
Artificial intelligence approaches such as genetic
algorithm (GA), particle swarm optimisation (PSO),
fuzzy logic and neural networks have been utilised
in system identification applications. Among these
GAs have shown great potential in parametric
modelling of dynamic systems.
The utilisation of binary-coded GA (BCGA) and
real-coded GA (RCGA) for parameter estimator of
models of dynamic systems has been reported in
various applications. Zamanan et al. (2006) have
reported the use of RGA as an optimization
technique for tracking harmonics on power systems.
Mitsukura et al. (2002) have reported using BCGA
and RCGA to (i) determine a function type and (ii)
the coefficient of the function and time delay,
respectively. They have tested the technique
successfully in determining the hammer stain model
and music data model. BCGA also has been used to
estimate the parameters of a plate structure (Intan,
2002). However, precision in BCGA is affected due
to the processes of encoding and decoding.
Moreover, BCGA is susceptible to the Hamming
Cliff effect, which can be problematic when
searching a continuous search space. Instead of
working on the conventional bit by bit operation in
BCGA, an RCGA approach is chosen in a wide
range of applications where both the crossover and
mutation operators are handled with real-valued
numbers. A real coded GA leads to reduced
computational complexity and faster convergence
compared to a binary coded GA.
In this work, RCGA is proposed for parametric
modeling of a flexible plate structure in comparison
to a binary-coded GA. The rest of the paper is
structured as follows: Section 2 describes the
flexible plate system and formulates the problem.
Section 3 presents the parametric models with
RCGA and parametric system identification
respectively. Section 4 presents implementation of
124
Md Salleh S., O. Tokhi M. and F. Toha S. (2009).
REAL-CODED GENETIC ALGORITHM IDENTIFICATION OF A FLEXIBLE PLATE SYSTEM.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 124-129
DOI: 10.5220/0002207801240129
Copyright
c
SciTePress
the algorithms in modeling the system using various
excitation signals such as finite duration step,
random and pseudo random binary signal (PRBS).
Results and discussions of the model validity
through input/output mapping, mean square of
output error and frequency domain response are also
presented. Parametric modelling is also confirmed
with convergence of fitness values and time run.
Finally, the paper is concluded in Section 5.
2 THE FLEXIBLE PLATE
SYSTEM
Dynamic simulation of a plate structure using the
finite differences (FD) method is considered in this
paper. The finite difference method is used to
discretise the governing dynamic equation
considered with no damping and the lateral
deflection of plates is obtained using central finite
difference method. It then transformed into state
space equation as the following equation.
W
i,j,k+1
= (A+2
ijk
)W
i,j,k
+ BW
ijk
+ CF (1)
Where 2
ijk
represents the diagonal elements of (2/c),
C=(
Δ
t
2
/
ρ
), c=-DC, and W
i,j,k+1
is the deflection of
grid points i = 1, 2,……, n+1 and j = 1, 2,.., m+1 at
time step k+1. W
i,j,k
and W
ijk
are the corresponding
deflections at time steps k and k-1 respectively. A is
constant (n+1)(m+1) x (n+1)(m+1) matrix whose
entries depend on physical dimensions and
characteristics of the plate, B is a diagonal matrix of
-1 corresponding to W
i,j,k
and C is a scalar related to
the given input and
F
is an (n+1)(m+1) x 1 matrix
known as the forcing matrix. The algorithm is
implemented in Matlab/SIMULINK with applied
external force or disturbance into all clamped edges
plate. Twenty two equal divisions of plate elements
with dimension 1.0mm× 1.0mm× 0.00032m is
measured at the detection and observation points
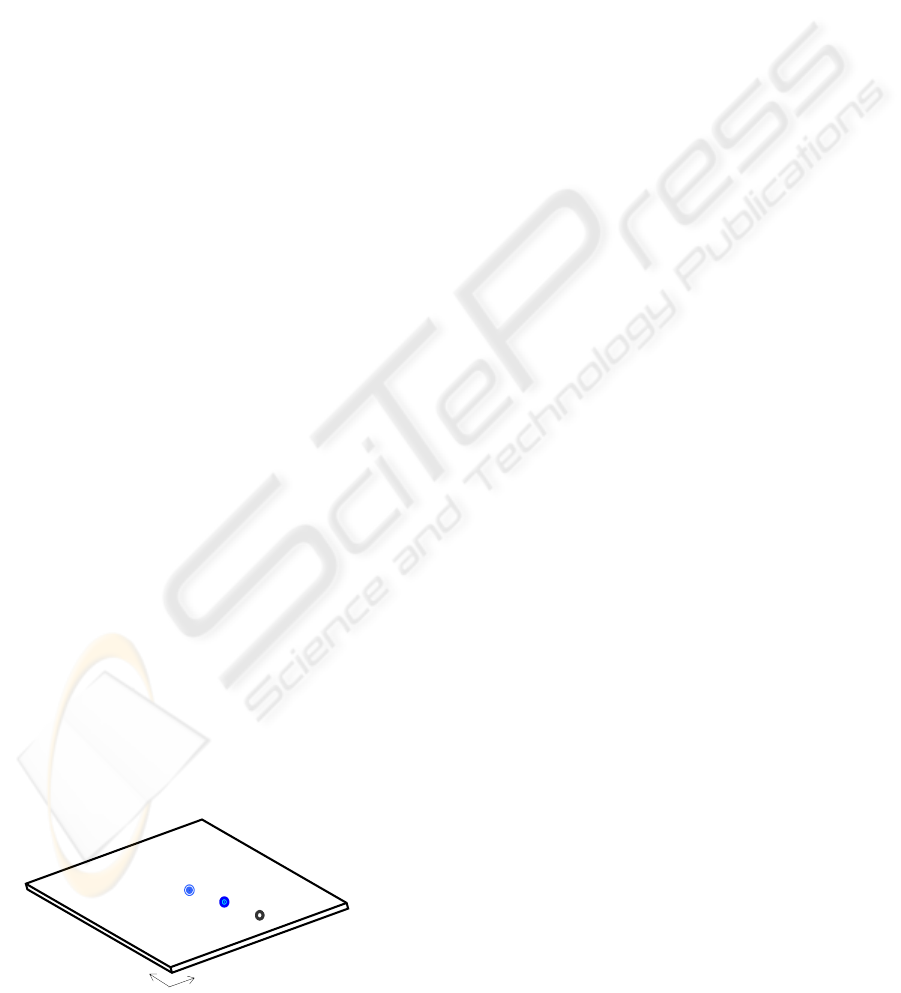
(Figure 1). Parameters of the plate considered
comprise mass density per area, ρ = 2700 kg/m
2
,
Young’s Modulus, E = 7.11 x 10
10
N/m
2
, second
moment of inertia, I = 5.1924 x 10
-11
m
2
and Poisson
ratio, υ = 0.3 with sampling time 0.001.
Detector
Observer
Primary Source
(12Δx, 12Δy)
(14Δx, 10
Δ
y)
(17Δx, 7Δy)
x
y
Δx = 45.455 mm
Δy = 45.455 mm
12Δx, 12Δy
17Δx, 17Δy
14Δx, 14Δy
Figure 1: The flexible plate system.
3 REAL CODED GENETIC
ALGORITHM
In most of practical engineering problems, the real-
coded GA is more suitable than the binary-coded
GA, as transformations from real number to binary
digits may suffer from loss of precision. Genetic
operations are very important to the success of
specific GA applications. In this work, real-coded
representation is used to determine the model order
of the plant and subsequently identify parametric
model of the system. The initial population is
created randomly within [-1,1] range. The main
three genetic operators involved are described
below.
3.1 Selection
Selection is the process of determining the number
of times or trials a particular individual in the
population is chosen for reproduction (Chipperfield,
1994). The process includes two steps, namely
selection probability and sampling algorithm.
Selection probability is concerned with
transformation of raw fitness values into real as
expected of an individual to reproduce. Sampling
algorithm reproduces individuals based on the
selection probabilities computed before. This
process is repeated as often as individuals must be
chosen. There are many methods reported such as
roulette wheel selection, stochastic universal
sampling and tournament selection, etc. The
stochastic universal sampling (SUS) method is used
in this work that randomly copies chromosomes and
simulates N equally distributed pointers. SUS is a
simpler algorithm, and as individuals are selected
entirely on their position in the population, SUS has
zero bias. After selection has been carried out, the
construction of the intermediate population is
complete and the crossover and mutation operators
are then applied.
3.2 Crossover (Recombination)
Crossover produces new individuals that have some
parts of both parent’s genetic material (Chipperfield,
1994). However, Mühlenbein et. al (1991) have
distinguished between recombination and crossover.
The mixing of the variables was called
recombination and the mixing of the values of a
variable was named crossover. Line recombination
employed in this work performs an exchange of
variable values between the individuals. By using a
real-valued encoding of the chromosome structure,
REAL-CODED GENETIC ALGORITHM IDENTIFICATION OF A FLEXIBLE PLATE SYSTEM
125

line recombination is a method of producing new
phenotypes around and between the values of the
parents’ phenotypes (Mühlenbein and Schlierkamp,
1993). For the line recombination, let
),...,(
1 n
xxx = and ),...,(
1 n
yyy = be the parent strings.
Then, the offspring
),...,(
1 n
zzz = is computed by
)(
iiii
xyxz −+=
α
ni ,...,1=
(2)
where
α
is chosen uniform randomly in [-0.25,
1.25]. Each variable in the offspring is the result of
combining the variables in the parents according to
(2). Line recombination can generate any point on
the line defined by the parents within the limit of the
perturbation,
α
, for a recombination in two
variables. This operator can overcome limitations in
variables decision and help improve in exploration
during recombination.
3.3 Mutation
The mutation operator arbitrarily alters one or more
components, genes, of a selected chromosome so as
to increase the structural variability of the
population. The role of mutation in GAs is that of
restoring lost or unexplored genetic material into the
population to prevent the premature convergence of
GA to suboptimal solutions; it insures that the
probability of reaching any point in the search space
is never zero. Each position of every chromosome in
the population undergoes a random change
according to a probability defined by a mutation
rate, the mutation probability, p
m
(Herrera et.al,
1998). The probability of mutating a variable is set
to be inversely proportional to the number of
variables (dimensions). The more dimensions one
individual has the smaller the mutation probability
of it will be. A mutation rate of 1/m, (where m is the
number of variables) produced good results for a
broad class of test function. However, the mutation
rate was independent of the size of the population
(Mühlenbein and Schlierkamp, 1993). The mutation
operator for the real coded GA uses a non-linear
term for the distribution of the range of mutation
applied to gene values. Real value mutation is used
in this work.
3.4 The Fitness Function
In this study, minimum mean square error is used as
a fitness function of the algorithm, while number of
generations is used as stopping criterion. The fitness
function, X, is set to minimize (3), in such a way
that it approaches zero;
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
∑
=
2
n
1i
iyiy
n
1
X )(
ˆ
)(min
(3)
where y(i) is the actual system output subjected to a
disturbance signal,
)(
ˆ
iy is the response of the
estimated system under the same disturbance, and
i=1,2,…,n ; n is total number of input/output sample
pairs. The algorithm of all executions predefined a
maximum number of generations as stopping
criteria.
3.5 Values of Real-coded Genetic
Parameters
The real-coded GA parameters used are presented in
Table 1.
Table 1: Parameters of real-coded GA.
RCGA Properties
Population Size 100
Selection rate 0.9
P
c
,
max
, P
c
,
min
0.67
P
m
,
max
, P
m
,
min
1/n (n=no of variables)
Selection Metho
d
SUS
Crossove
r
Metho
d
Line Recombination
Mutation method Real-value mutation
4 PARAMETRIC SYSTEM
IDENTIFICATION
The transfer function of the model used corresponds
to the ARMA model structure by neglecting the
noise,
η
term;
4)-u(k
3
b1)-u(k
0
b
4)-y(k
4
a--1)-y(k
1
a(k)y
+…++
…−=
ˆ
(4)
In matrix form, the above equation can be written as
T
4ku3ku
2ku1ku
3
b
2
b
1
b
0
b
T
4ky3ky
2ky1ky
4
a
3
a
2
a
1
a
ky
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−−
−−
+
−−
−−
−=
)(),(
),(),(
,
,,
)(),(
),(),(
,
,,
)(
(5)
The first four variables are assigned to b
0
,…,b
3
and the next four to a
1
,…,a
4
as indicated in (5). Once
the model is determined, the model needs to be
verified to determine whether it is well enough to
represent the system. Correlation tests including
autocorrelation of the error, cross correlation of
input-error, input*input-error are carried out to test
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
126
and validate the model. Each simulation was
observed over 7000 samples of data for each set.
The first five resonance frequencies of vibration of
the plate found from spectral density of the predicted
output of the RCGA model were 9.971 rad/s, 34.51
rad/s, 56.76 rad/s, 78.23 rad/s and 99.71 rad/s.
5 RESULTS
In order to determine appropriate model order for
system model using RCGA, different model orders
were tested. The results of these tests with model
orders of 4 to 12 are summarized in Table 2. The
results include time run, standard deviation, mean
value and mean square error. The accuracy of the
model, for different model orders, is presented in
terms of standard deviation, mean value and MSE
normalized with 10
-15
, run time represented in
minutes, and values averaged for each 5 runs. As
noted in Table 2, a model order of 4 achieved
minimum mean square error of 1.195 with the
smallest standard deviation computational time, and
this was thus chosen for obtaining a model of the
flexible plate.
Table 2: Accuracy of model order.
Model
Order
4 6 8 10 12
Std.
Deviation
5.825 6.492 10.10 7.332 10.86
Mean
Value
2.208 2.383 2.996 3.097 3.939
Normal
MSE
1.195 1.203 1.196 1.281 1.562
Time Run
(min)
34.84 34.93 42.55 42.13 43.02
In subsequent attempts, model order of four
(4) has been used to obtain unknown parameters of
RCGA model system in comparison to binary coded
genetic algorithm (BCGA). In BCGA, the design
parameters are similar to those in RCGA with single
point crossover and mutation rate of 0.0001. For
RCGA, the time-domain and frequeny-domain
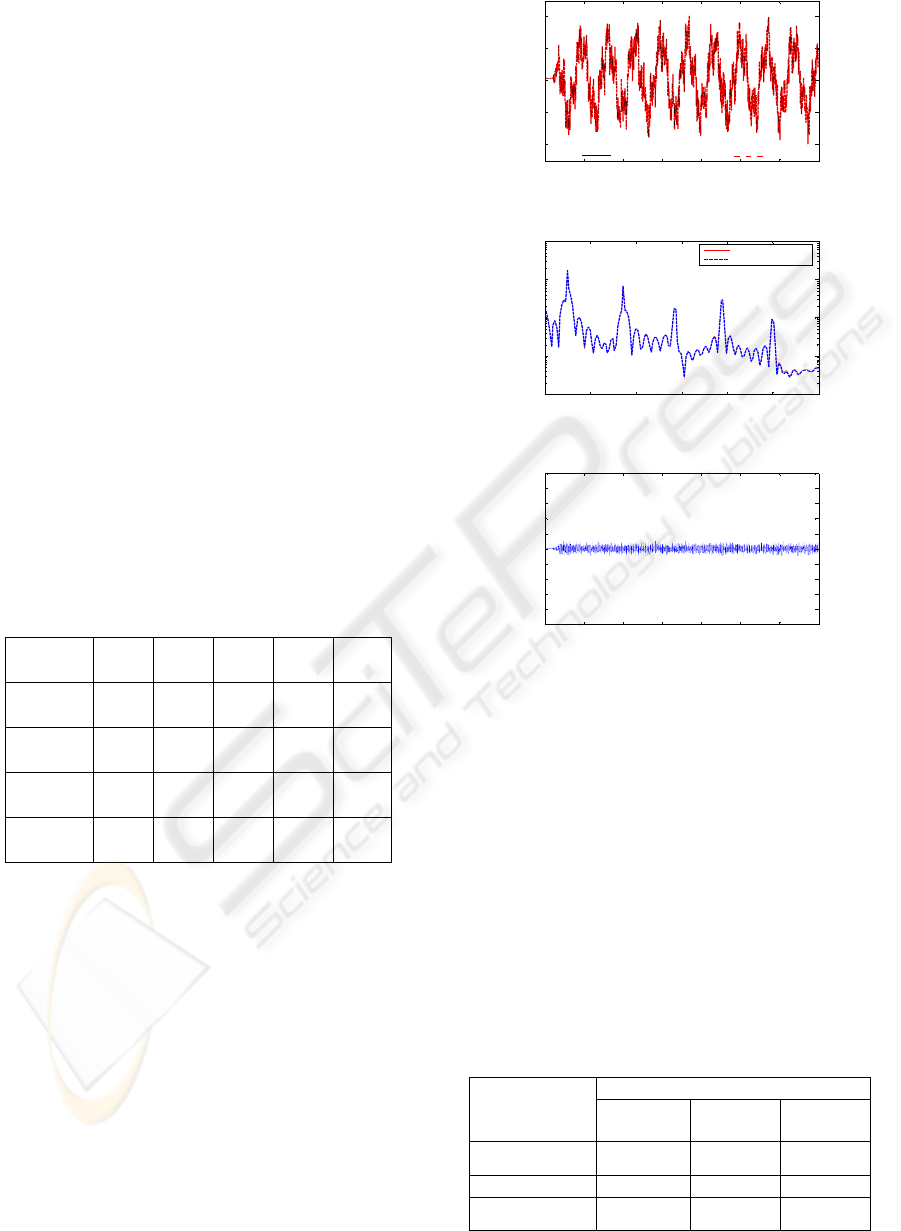
results with random disturbance are shown in Figure
2 and Figure 3 respectively. Both figures show
agreement between the actual and predicted output
in modelling the plate. The normalized error
between the two outputs as depicted in Figure 4 is
0 1 2 3 4 5 6 7
-1
-0.5
0
0.5
1
RCGA-EstimatedTarget
Time
(
sec
)
Deflection (Normalised
)
Figure 2: The error between actual- predicted outputs.
0 20 40 60 80 100 120
10
0
10
1
10
2
10
3
10
4
Fre
q
uenc
y,
rad/s
Magni t ude(dB)
Target
RCGA-Estimated
Figure 3: PSD of the actual-predicted outputs.
0 1 2 3 4 5 6 7
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Time
(
sec
)
Error (normalised
)
Figure 4: Error between the actual-predicted outputs.
reasonably small. The corresponding correlation test
results are shown in Figure 5 using random signals
for RCGA, and these are in general within the 95%
confidence level. Thus, this confirms the accuracy of
the model in representing the dynamic behaviour of
the plant system.
Small or less significant parameter variations
with BCGA indicate convergence to local minima
and/or pre-mature convergence.
The MSE values
achieved after 500/1000 generations (Figure 6 –
Figure 8) with BCGA and RCGA are shown in
Table 3. RCGA achieved faster convergence
compared to BCGA. The RCGA achieved better
convergence than BCGA over 500 generations or less
Table 3: Mean squared output error with the Gas.
Algorithm
(Generation)/
Disturbance
Mean Squared Error
Random
(x10
-4
)
PRBS
(x10
-4
)
Step
(x10
-6
)
RCGA (500 ) 9.51350 1.83940 1.022
RCGA (1000) 9.51070 1.84130 1.199
BCGA (500) 12.02200 4.41720 7.6564
REAL-CODED GENETIC ALGORITHM IDENTIFICATION OF A FLEXIBLE PLATE SYSTEM
127

-5000 -4000 -3000 -2000 -1000 0 1000 2000 3000 4000 5000
-1
-0.5
0
0.5
1
lag
(a) Auto-correlation of residuals
-5000 -4000 -3000 -2000 -1000 0 1000 2000 3000 4000 5000
-1
-0.5
0
0.5
1
lag
(b) Cross-correlation of input and residuals
-5000 -4000 -3000 -2000 -1000 0 1000 2000 3000 4000 5000
-1
-0.5
0
0.5
1
lag
(c) Cross-correlation of input square and residuals
-5000 -4000 -3000 -2000 -1000 0 1000 2000 3000 4000 5000
-1
-0.5
0
0.5
1
lag
(d) Cross-correlation of input square and residual square
-5000 -4000 -3000 -2000 -1000 0 1000 2000 3000 4000 5000
-1
0.5
0
0.5
1
lag
(e) Cross-correlation of residuals and (input*residuals)
Figure 5: Correlation validation tests (a) – (e).
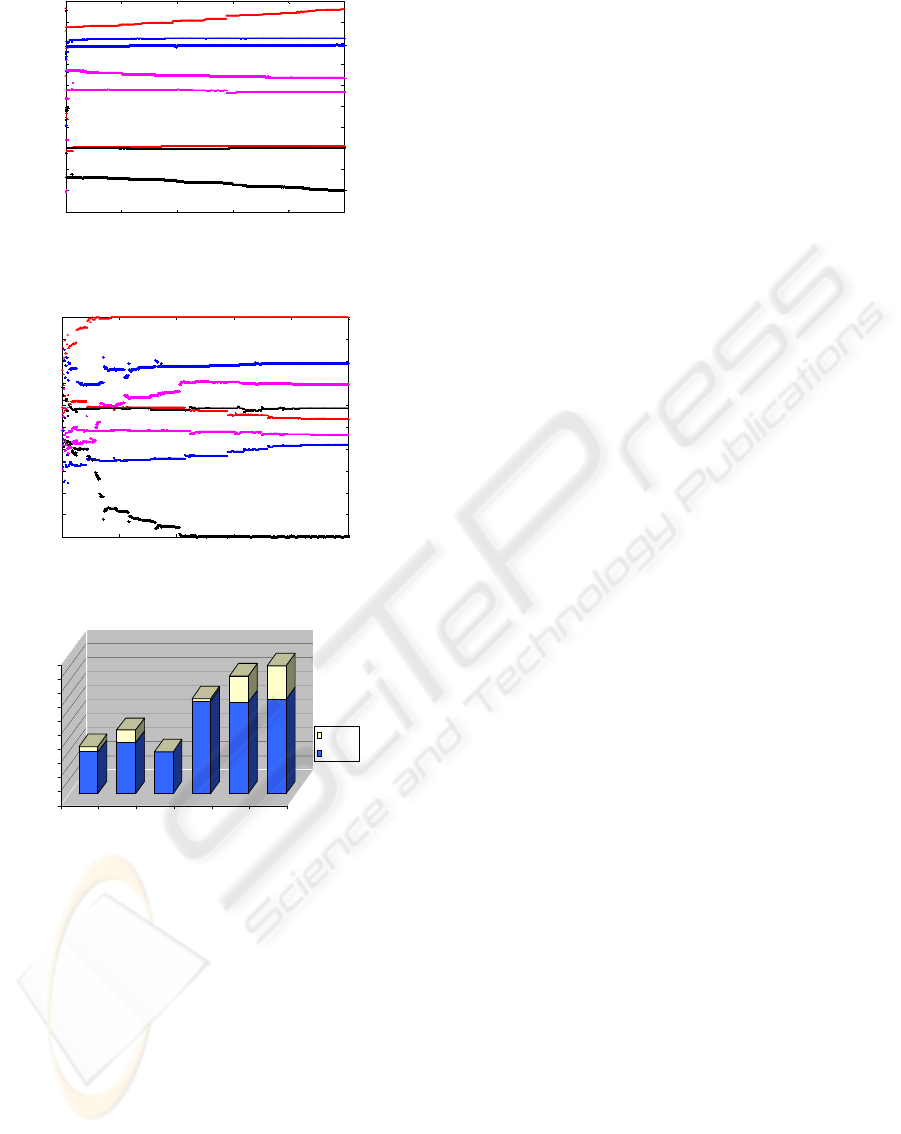
(recommended about 350) with all the test signals. It
was noted that a larger number of generations did
not improved the convergence rate, but took more
time to compute. Figures 9 and 10 show the
convergence of parameter estimates with RCGA as
compared to BCGA.
The estimated system model parameters [a1, a2,
a3, a4, b0, b1, b2, b3] with the tested disturbance
signals at the end of 500 generations with RCGA
and BCGA are shown below.
i) Random disturbance
RCGA: [0.07336, 0.1579, 0.1716, 0.07099, 1,
0.5824, –1, 0.392],
BCGA: [–0.375, 0.6445, –0.107, 0.1354, 0.9176,
0.5837, –0.7937, 0.2734]
ii) PRBS
RCGA: [0.1355, –0.2193, 0.3892, –0.2897,
1,0.6084, –1, 0.3739]
BCGA: [–0.5263, 0.3177, 0.0453, 0.3203, 1,
0.3285, –0.9275, 0.5801]
iii) Finite duration step
RCGA: [0.1850, –0.0002, –0.5244, 0.3418, 1,
0.4964, –0.0352, –0.4639],
BCGA: [–0.0576, 0.7715, –0.9993, 0.3186,
0.4695, 0.3206, 0.4653, –0.4607]
Figure 11 shows the MSE (in 10
-4
) and
associated computer run time (in hours) for
convergence with RCGA and BCGA. It is noted that
in general the RCGA required less computing time
as well as achieved lower MSE values as compared
to BCGA.
0 100 200 300 400 500 600 700 800 900 1000
-3.2
-3
-2.8
-2.6
-2.4
-2.2
-2
-1.8
-1.6
Generation
log10(f(x))
Real-Coded GA 1000 generation
Binary-Coded GA 500 generation
Real-Coded GA 500 generation
Figure 6: Convergence with random signal.
0 100 200 300 400 500 600 700 800 900 1000
-3.8
-3.6
-3.4
-3.2
-3
-2.8
-2.6
-2.4
-2.2
-2
-1.8
Generation
log10(f(x))
Real-Coded GA 1000 generation
Binary-Coded GA 500 generation
Real-Coded GA 500 generation
Figure 7: Convergence with PRBS Signal.
0 100 200 300 400 500 600 700 800 900 1000
-6
-5.5
-5
-4.5
-4
-3.5
-3
-2.5
-2
Generation
log10(f(x))
Real-coded GA 1000 generation
Real-coded GA 500 generation
Binary-coded GA 500 generation
Figure 8: Convergence with step signal.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
128
0 100 200 300 400 500
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Generation
Estimated a and b Parameters
b3
b0
a2
b1
a4
a1
a3
b2
Figure 9: Estimated parameters with BCGA.
0 100 200 300 400 500
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Generation
Estimated a and b Parameters
b0
b1
b3
a3
a1
a4
a2
b2
Figure 10: Estimated parameters with RCGA.
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
4.00
4.50
5.00
RCGA
PRBS
BCGA
PRBS
RCGA
Step
BCGA
Step
RCGA
Random
BCGA
Random
Al
g
orithm & Si
g
nal
MSE
Tim e run
Figure 11: MSE and time run for GAs.
6 CONCLUSIONS
Parametric modelling of a flexible plate system has
been carried out. Real-coded GA has been used for
estimation of order and parameters of the model
characterising the dynamic behaviour of the plate
system. The approach has been evaluated in
comparison to equivalent binary-coded GAs with
three different test signals. It is noted that the models
obtained with RCGA have performed better in
characterising the system in comparison to those
obtained with BCGA.
ACKNOWLEDGEMENTS
The author acknowledges the support of a research
fellowship of the University Tun Hussein Onn
Malaysia (UTHM) and Ministry of Higher
Education Malaysia.
REFERENCES
Chipperfield, A. J., Fleming, P. J., Pohlheim, H. and
Fonseca, C., 1994. A genetic algorithm toolbox for
MATLAB, Proceedings of the International
Conference on Systems Engineering, Coventry, UK.
Herrera, F., Lozano, M., Verdegay, J.L., 1998. Tackling
real-coded genetic algorithms: operators and tools for
behavioural analysis, Artificial Intelligence Review,
Vol. 12, pp. 265-319.
Mat Darus, I.Z., 2004. Soft computing Adaptive Active
Vibration Control of Flexible Structures, PhD Thesis,
Dept. of Automatic Control and Systems Engineering,
The University of Sheffield, Sheffield, UK.
Md Salleh, S., Tokhi, M.O., “Discrete Simulation of a
Flexible Plate Structure using a State-Space
Formulation”, Proceedings of 7th International
Conference on System Simulation and Scientific
Computing (ICSC’2008), Beijing China, 10-12 Oct
2008.
Mitsukura, Y.,M., Fukumi, Norio Akamatsu and
Yamamoto,T. , 2002. A System Identification Method
Using a Hybrid-Type Genetic Algorithm, Proceedings
of the 41st SICE Annual Conference, Vol.3 ,pp.1598-
1602.
Mühlenbein, H., and Schlierkamp-Voosen, D., 1993.
Predictive Models for the Breeder Genetic Algorithm:
I. Continuous Parameter Optimization, Evolutionary
Computation, Vol.1, issue 1, pp. 25-49.
Mühlenbein, H. , Schomisch, M., and Born, J., 1991. The
parallel genetic algorithm as function optimizer,
Parallel Computing, 17, pp. 619-632.
Shaheed, M.H. and Tokhi, M.O., 2002. Dynamic
modelling of single-link flexible manipulator:
parametric and non-parametric approaches, Robotica,
20, pp. 93–109.
Zamanan, N.; Sykulski, J.K.; Al-Othman, A.K., Real
Coded Genetic Algorithm Compared to the Classical
Method of Fast Fourier Transform in Harmonics
Analysis, Proceedings of the 41
st
International UPEC
'06, Vol. 3, pp. 1021-1025.
REAL-CODED GENETIC ALGORITHM IDENTIFICATION OF A FLEXIBLE PLATE SYSTEM
129
