ON THE WORK-IN-PROCESS CONTROL OF PRODUCTION

NETWORKS

Nikos C. Tsourveloudis

Machine Tools Laboratory, Technical University of Crete, Chania, Greece

Keywords: Production Networks, Work-In-Process, Fuzzy Control, Evolutionary Algorithms, Controller Design.

Abstract: The effectiveness of evolutionary optimized fuzzy controllers for production scheduling has been proven in

the past. The objective of the control/scheduling task in this context, is to continuously adjust the production

rate in a way that: 1) satisfies the demand for final products, 2) keeps the inventory as low as possible. The

evolutionary optimization identifies fuzzy control solutions which simultaneously satisfy those restrictions.

The important question here is: How robust and generic is the outcome of the evolutionary process? In this

paper we face this question by testing the evolutionary tuned fuzzy controllers under several demand

patterns, as the actual demand might be different from those used for evolution\optimization. Extensive

simulations of a supervisory controller identify the performance of the evolutionary-fuzzy strategy in

comparison to a pure knowledge based one.

1 INTRODUCTION

As the manufacturing industry moves away from the

mass production paradigm towards the agile

manufacturing, the life cycle of products gets shorter

while the need for a wide variety of them increases.

Keeping large inventories in stock tends to be

unattractive in today’s markets. The same holds for

the unfinished parts throughout the manufacturing

system, widely known as Work-In-Process (WIP), as

it represents an already made expense with unknown

profitability due to the rapidly changing demand. In

a highly changing demand environment, the

accumulated inventories are less desirable than ever.

The work-in-process inventory is measured by

the number of unfinished parts in the buffers

throughout the manufacturing system and it should

stay as small as possible (Conway et al., 1998), (Bai

and Gershwin, 1994).

Traditionally, inventory control methods in this

field can be roughly grouped into mathematical

modelling approaches, computerized planning

methods, such as material requirement planning

(MRP), and heuristic scheduling strategies. Many

ontrol policies (CONWIP-constant WIP, base stock

method etc.|) aim in keeping WIP at low levels

(Gershwin, 1994). However, an exact optimal value

of WIP cannot be determined in realistic

manufacturing conditions. Therefore, the problem of

WIP determination and control is amenable to an

artificial intelligent treatment, as suggested in

(Custodio et al., 1994), (Tsourveloudis et al., 2000)

and recently in (Ioannidis et al., 2004) and

(Tsourveloudis et al., 2006).

The supervisory

controller suggested in (Ioannidis et al., 2004) is used

to tune a set of lower-level distributed fuzzy control

modules that reduce WIP and synchronize the

production system's operation. The overall control

objective is to keep the WIP and cycle time as low as

possible, while maintaining quality of service by

keeping the backlog to an acceptable level.

Fuzzy logic has been used in tandem to

Evolutionary Algorithms (EA) so as to keep the WIP

and cycle time as low as possible, and at the same

time to maintain high utilization (Tsourveloudis et

al. 2006, Tsourveloudis et al., 2007). The objective

in those works was to optimize the control policy in

a way that satisfies the (random) demand for final

products while keeping minimum WIP within the

production system. During the evolution, the EA

identifies those set of parameters for which the fuzzy

controller has an optimal performance with respect

to WIP minimization for several demand patterns.

The use of evolving genetic structures for the

production scheduling problem, has recently gained

a lot of acceptance in the automated and optimal

design of fuzzy logic systems (Tedford and Lowe,

2003, Gordon et al. 2001). However, a potential

222

C. Tsourveloudis N. (2009).

ON THE WORK-IN-PROCESS CONTROL OF PRODUCTION NETWORKS.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,

pages 222-227

DOI: 10.5220/0002208202220227

 SciTePress

problem is that the evolutionary (or genetically)

evolved fuzzy controllers might perform optimal

only under the conditions involved in the evolution

process. In this paper we examine the performance

of evolutionary optimized controllers in contrast to

heuristically designed fuzzy controllers. For

comparisons purposes we test the controllers in

conditions different from the ones they have been

designed for. In this way, some useful insights

regarding the design robustness of the evolutionary

tuned fuzzy controllers may be drawn.

The rest of the paper is organized as follows.

Section 2 describes the evolutionary fuzzy

scheduling concept that is used for WIP

minimization. Two control approaches are

presented: the distributed and the supervised one.

Section 3 describes the comparison scenarios and

presents experimental results for production lines

and networks. Issues for discussion and remarks as

well as suggestions for further development are

presented in the last section.

2 EVOLUTIONARY-FUZZY

SCHEDULING

A production network consists of machines

(operation stations) and buffers (storage areas).

Items are received at each machine and wait for the

next operation in a buffer with finite capacity. WIP

may increase because of unanticipated events, like

machine breakdowns and potential consequent

propagation of these events. For example, a failed

machine with operational neighbours forces to an

inventory increase of the previous storage buffer. If

the repair time is big enough, then the broken

machine will either block the previous station or

starve the next one. This “bottleneck” effect will

propagate throughout the system.

Clearly, production scheduling of realistic

manufacturing plants must satisfy multiple

conflicting criteria and also cope with the dynamic

nature of such environments. Fuzzy logic offers the

mathematical framework that allows for simple

knowledge representations of the production

control/scheduling principles in terms of IF-THEN

rules. The expert knowledge that describes the

control objective (that is WIP reduction) can be

summarized in the following statements

(Tsourveloudis et al, 2000, Tsourveloudis et al.,

2006):

If the surplus level is satisfactory then try to

prevent starving or blocking by increasing or

decreasing the production rate accordingly,

else

If the surplus is not satisfactory that is either too

low or too high then produce at maximum or zero

rate respectively.

In fuzzy logic controllers (FLCs), the control

policy is described by linguistic IF-THEN rules

similar to the above statements. The essential part of

every fuzzy controller is the knowledge acquisition

and the representation of the extracted knowledge

with certain fuzzy sets/membership functions.

Membership functions (MFs) represent the

uncertainty modelled with fuzzy sets by establishing

a connection between linguistic terms (such as low,

negative, high etc) and precise numerical values of

variables in the physical system. The correct choice

of the MFs is by no means trivial and plays a crucial

role in the success of an application. If the selection

of the membership functions is not based on a

systematic optimization procedure then the adopted

fuzzy control strategy cannot guarantee minimum

WIP level.

The evolutionary-fuzzy synergy attempts to

minimize the empirical/expert design and create

MFs that fit best to scheduling objectives

(Tsourveloudis et al., 2006). In this context, the

design of the fuzzy controllers (distributed or

supervisory) can be regarded as an optimization

problem in which the set of possible MFs constitutes

the search space. Evolutionary Algorithms (EAs) are

seeking optimal or near optimal solutions in large

and complex search spaces and therefore have been

successfully applied to a variety of scheduling

problems with broad applicability to manufacturing

systems (Tedford and Lowe, 2003). The objective is

to optimize a performance measure which in the

EAs context is called fitness function. In each

generation, the fitness of every chromosome is first

evaluated based on the performance of the

production network system, which is controlled

through the membership functions represented in the

chromosome. A specified percentage of the better

fitted chromosomes are retained for the next

generation. Then parents are selected repeatedly

from the current generation of chromosomes, and

new chromosomes are generated from these parents.

One generation ends when the number of

chromosomes for the next generation has reached

the quota. This process is repeated for a pre-selected

number of generations.

2.1 Distributed Evolutionary-fuzzy

Control

The architecture of the distributed evolutionary-

fuzzy WIP control scheme is extensively discussed

ON THE WORK-IN-PROCESS CONTROL OF PRODUCTION NETWORKS

223

() (() ())

ijj

Fx Dt PRt

−

⎡⎤

=−

⎢⎥

⎣⎦

∑

(, ,,)

ji il i i

bbxs

in (Tsourveloudis et al., 2006) and (Tsourveloudis et

al., 2007). The control objective of the distributed

scheduling approach, as earlier stated, is to satisfy

the demand and, at the same time, to keep WIP as

low as possible. This is attempted by regulating the

processing rate r

at every time instant. The

processing rate r

of each machine at every time

instant is:

⎪

⎩

⎪

⎨

⎧

∑

′

1if

)(

0if0

),,,(

,,IS

iRi

iiliiji

sxbbr

, (1)

where, represents a fuzzy

inference system that takes as inputs the level

the upstream buffer, the downstream buffer level

, x

is the surplus (cumulative production minus

demand) and s

is a non fuzzy variable denoting the

state of the machine, which can be either 1

(operative) or 0 (stopped).

The fitness function F(x

) of each individual x

which associates the demand with the cumulative

production of the manufacturing system is:

(2)

where, t is the current simulation time, D(t) is the

overall demand and PR(t) is the cumulative

production of the system.

As earlier stated, the objective of the evolution

process is to optimize the shape of the fuzzy

membership function. Indeed, after the evolution

process the shape of the membership functions is

altered. The best individual is considered to be the

one with the biggest fitness. The fittest individuals

are selected and they undergo mutations. The fittest

controllers and their mutated offsprings are forming

the new population. After some generations the

algorithm converges and the best individuals

represent near optimal solutions.

2.2 Supervised Evolutionary-fuzzy

Control

In control systems literature a supervisor is a

controller (supervisory controller) that utilizes

available data to characterize the overall system's

current behavior, potentially modifying the lower

level controllers to ultimately achieve desired

specifications. The supervisory controller in this,

and also in our past works, is used to tune the

distributed controllers in a way that improves

performance without dramatic changes in the

structure of the control architecture, as justified in

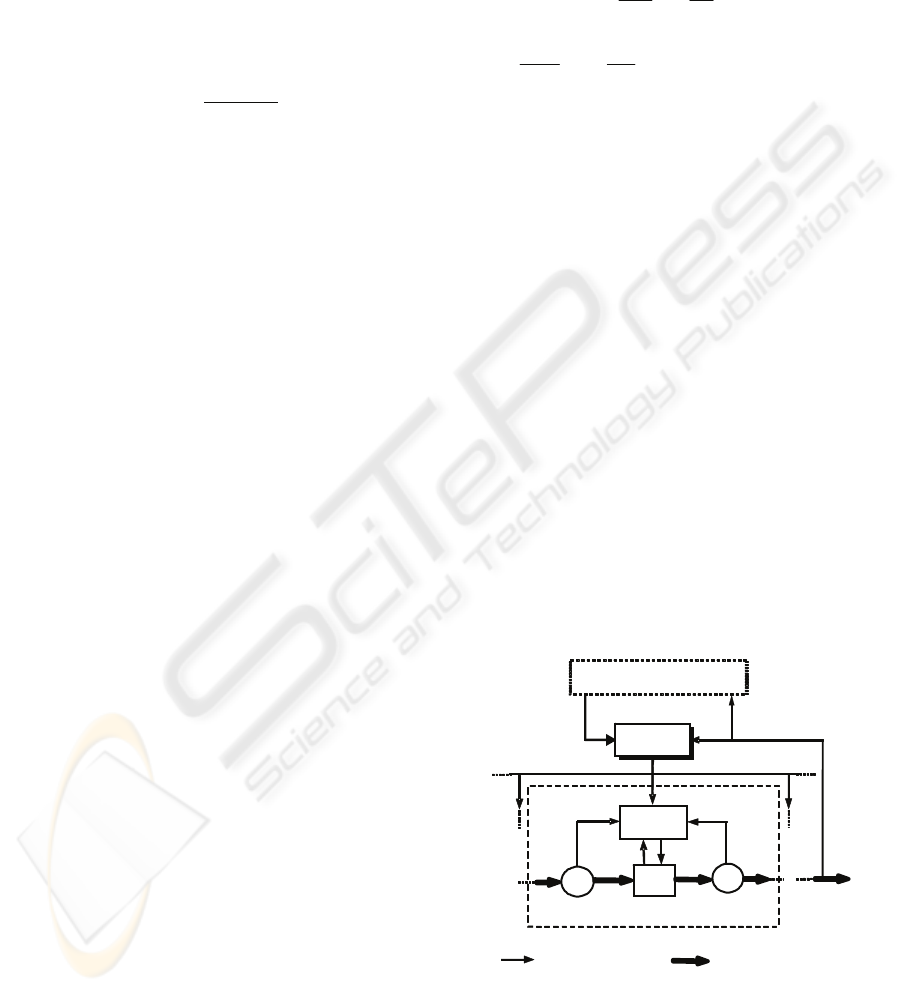
(Ioannidis et al., 2004). The concept of the

supervised evolutionary-fuzzy WIP control scheme

is shown in Figure 1. The fitness function in the

supervisory approach case was chosen to be the

following:

()

cWIP c BL

−

(3)

where,

WIP

and

are the mean work-in-process

and mean backlog (=cumulative production minus

demand), respectively. The c

, c

are weighting

factors that represent the unit costs of inventory and

backlog, respectively. Assuming that the capacity of

a production system is given, equations (2) and (3)

show that the evolved MFs are highly based (in

terms of their support and shape) on the demand

values. Obviously, the value of demand is crucial for

WIP and backlog determination in (3). Some of the

questions arise here concerning demand, are:

• What happens when actual demand is different

(in both magnitude and changing pattern) than

the one considered during controller’s

evolution?

• Is the evolved controller robust enough to

absorb random variations of demand?

• Does the original (without MF optimization)

heuristic fuzzy controller perform better in

unknown demands?

Since there are no analytical solutions to those

questions, in what follows we will examine and

compare the performance of both evolutionary and

heuristic fuzzy controllers through simulation, for a

variety of test cases.

volutionary Algorithm

j,i

Controlle

Supervisory

Controlle

roduction Control Module

: Information Flow

: Material Flow

Figure 1: Supervisory control: Evolutionary-fuzzy

concept.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

224

3 TESTING AND RESULTS

The evolutionary-fuzzy approaches suggested in

(Tsourveloudis et al., 2007), are tested and

compared to the heuristic fuzzy approaches initially

suggested in (Tsourveloudis et al., 2000). In the all

simulations performed we assume that the machines

fail randomly, with a failure rate p

. This rate is

known and set before the simulation starts. Also,

machines are repaired randomly with rate rr

. The

resources needed for repairs are assumed to be

available. The times between failures and repairs are

exponentially distributed. All machines operate at

known, but not necessarily equal rates. Each

machine produces in a rate r

≤ µ

, where μ

is the

maximum processing rate of machine M

. We also

assume that the flow of parts within the system is

continuous.

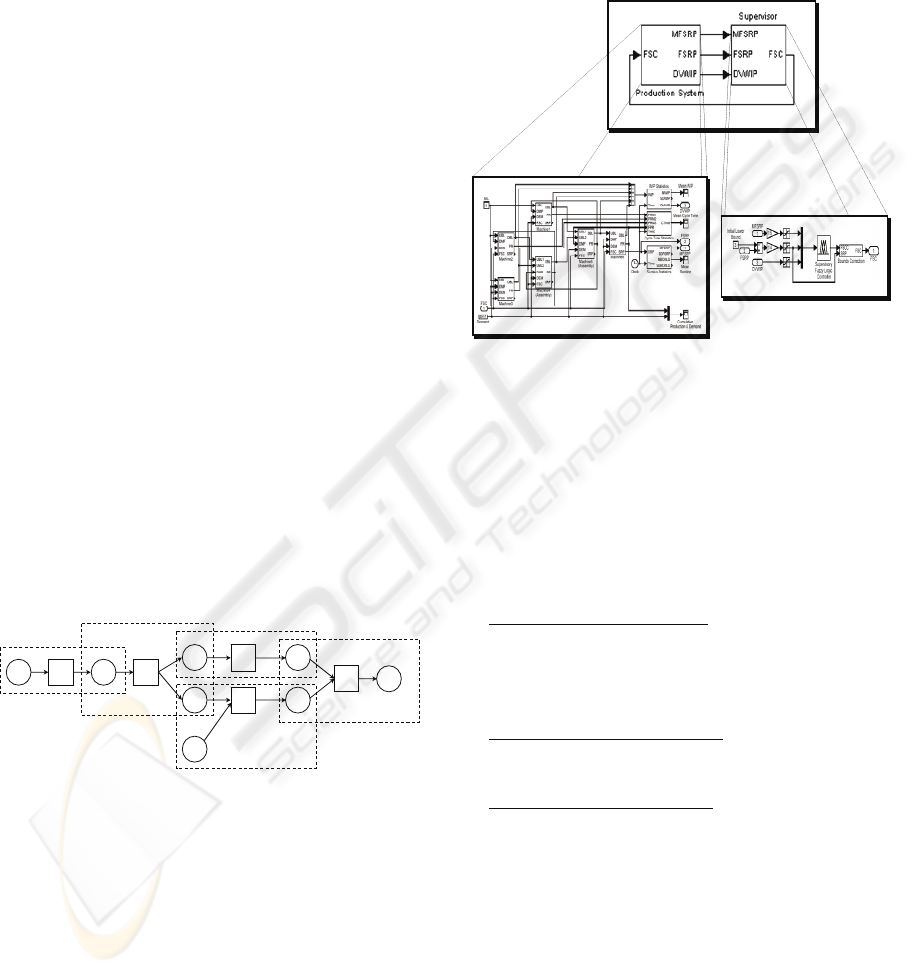
In the production network shown in Figure 2, the

circles represent buffers and squares are machining

stations. This network is identical to the one

discussed in previous works (Tsourveloudis et al.,

2000, 2006a, 2006b, 2007). For simplicity it is

assumed that this network produces one part type.

Lines and networks producing multiple part types

have been discussed in (Tsourveloudis et al., 2000),

(Ioannidis et al., 2004) and it has been shown that

have similar behavior to the single-part-type

systems. One important observation made in

(Ioannidis et al. 2004, Tsourveloudis et al. 2006,

2007) was that the evolutionary tuned fuzzy

controllers achieved a substantial reduction of WIP

in almost all test cases.

1,2

2,4

4,5

2,3

3,5

Subsystem 1 (line)

Subsystem 2 (disassembly)

Subs

stem 3

(

line

)

Subsystem 4 (assembly)

Subsystem 5 (assembly)

Figure 2: Layout of the production network.

Here we further investigate the performance of the

evolutionary tuned fuzzy controllers, keeping

unaltered the controllers’ design but with demand

patterns that are significantly changed. In practice,

demand is the main uncertainty of almost all

production system/networks. Changes in demand

may cause significant problems in balancing

production lines

3.1 Supervised Control of Networks

The objective is to examine the robustness of the

supervised control approach. The simulation testbed

used for this test case was developed in SIMULINK

and its main blocks are shown in Figure 3.

Production system subsystem

Supervisor subsystem

Production system’s simulator

Figure 3: SIMULINK model of the supervisory control.

The performance of the evolutionary-fuzzy

supervised approach was examined for various

demand patterns other than the one used during the

optimization of the membership functions. During

the evolution procedure, demand was considered

either one (one product per time unit) or zero (no

demand at the time unit) and the selection between

those two values was triggered in a random order.

During our testing different demands were used:

Demand Pattern 1 (DP1)

: The system accepts

orders of 1 product per time unit. The time unit is set

equal to 0.05 of the simulation step. This is similar

to the demand pattern used for the optimization of

the controller.

Demand Pattern 1.5 (DP1.5)

: The system accepts

orders for 1.5 products per time unit, which is set

0.05 of the simulation step.

Demand Pattern 3 (DP3):

The system accepts

orders for 3 products per time unit, which is also set

0.05 of the simulation step.

Figure 4 presents the mean WIP and Backlog for

the above mentioned demand patterns. As it can be

seeing, the mean WIP of DP1 is higher than the

other two demands, but it fully satisfies the

requested demand. DP1.5 and DP3 fail in satisfying

demand in the same test run. It also can be seen, in

Figure 4, that when the demand is 3 times higher

(DP3) than the one used for the evolution (DP1),

then it cannot be satisfied as the backlog

accumulates rapidly (DP3-BL).

ON THE WORK-IN-PROCESS CONTROL OF PRODUCTION NETWORKS

225

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

-50

-40

-30

-20

-10

Simulat ion Time

DP1-WIP

DP1-BL

DP1.5-BL

DP1.5-WIP

DP3-WIP

DP3-BL

Figure 4: WIP and Backlog levels of the supervisory

control for various demand sizes.

However, when demand is increased for 50%,

(DP1.5) the unsatisfied demand (DP1.5-BL) is

almost zero which shows that the supervisor works

satisfactorily for demand changes of this magnitude:

+50% of the demand used during the evolution of

the fuzzy supervisory controller. This important

observation was also noted through a series of

simulation runs for demands lower than the one used

in the evolution. In this case, a slight increase in the

mean WIP levels was observed.

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

-40

-30

-20

-10

0.05-WIP

0.05-BL

0.5-BL

0.5-WIP

5-WIP

5-BL

Figure 5: WIP and Backlog levels for changing demand

rates.

Not only the magnitude but also the frequency of

demand changing was examined. Figure 5 presents

the WIP and Backlog mean levels when the DP1.5

demand pattern changes every 0.05, 0.5, and 5 time

units respectively. It can be observed that in lower

demand rates the controller keeps the backlog orders

close to zero, while in higher rates although the

controller keeps WIP in low levels, fails in satisfying

the demand (5-BL in Figure 5).

4 CONCLUSIONS

WIP itself cannot represent adequately of production

system's performance. One has to take into account

also the accumulated orders backlog. It is also

known that when demand is very high one may

consider that service rate and thus backlog is more

important than WIP. When demand can be easily

satisfied and backlog is in low levels, a substantial

reduction of WIP may be more important than a

small increase in backlog. What we have seen so far

is that with the aid of the evolutionary-fuzzy

controllers the system’s performance becomes more

balanced in terms of mean WIP and backlog. WIP is

substantially reduced in the evolutionary-fuzzy

approach compared to the empirical selected fuzzy

controllers. The same observation holds for the

supervisory control of production networks where

significantly increased demands were

accommodated.

The heuristic fuzzy control approach cannot

achieve the performance of the evolutionary-fuzzy.

However, it is still better than previously reported

“bang-bang” control approaches. Even when

compared to the evolutionary-fuzzy approach it is

much simpler in the design process as it steps on the

human expertise/knowledge regarding the

production system. In others words, one should very

fast design, built and put to work a fuzzy controller

with membership functions that represent the expert

knowledge in contrast to the evolutionary-fuzzy

system whose parameters are automatically set by

the optimization procedure.

The evolutionary-fuzzy controllers are capable of

maintaining low WIP levels for product demands

other than the ones used during the optimization.

Therefore, the evolutionary algorithms clearly

represent a successful approach towards the

optimization of robust scheduling approaches.

REFERENCES

Conway R., Maxwell W, McClain J.O., Joseph Thomas L,

1998. The role of work-in-process inventory control:

single-part-systems. Oper. Res. 36, pp. 229-241.

Bai S.X. and Gershwin S.B., 1994. Scheduling

manufacturing systems with work-in-process

inventory control: multiple-part-type systems. Int. J.

Prod. Res. 32, 365-386.

Gershwin S.B ., 1994. Manufacturing Systems

Mean Backlog

Mean WIP

Mean Backlog Mean WIP

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

226

Engineering. Prentice Hall, New Jersey.

Custodio L., Sentieiro J., Bispo C., 1994. Production

planning and scheduling using a fuzzy decision

system. IEEE Trans. Robot. Automat. 10, pp. 160-168.

Tsourveloudis N.C., Dretoulakis E., Ioannidis S., 2000.

Fuzzy work-in-process inventory control of unreliable

manufacturing systems. Inf. Sci. 27, pp. 69-83.

Ioannidis S., Tsourveloudis N.C., Valavanis K.P., 2004.

Fuzzy Supervisory Control of Manufacturing Systems.

IEEE Trans. Robot. Automat. 20, pp. 379-389.

Tsourveloudis N. C., L. Doitsidis, S. Ioannidis, 2006.

Work-in-Process Scheduling by Evolutionary Tuned

Distributed Fuzzy Controllers. In: Proceedings of the

IEEE International Conference on Robotics and

Automation, Orlando, FL, USA.

Tsourveloudis N. C., S. Ioannidis, K. P. Valavanis, 2006.

Fuzzy Surplus based Distributed Control of

Manufacturing Systems. Advances in Production

Engineering and Management. 1, pp. 5-12.

Tsourveloudis N. C, Doitsidis L., Ioannidis S., 2007.

Work-In-Process Scheduling by Evolutionary Tuned

Fuzzy Controllers. International Journal of Advanced

Manufacturing Technology. 34, no. 7-8, pp. 85-97.

Tedford J.D. and Lowe C., 2003. Production scheduling

using adaptable fuzzy logic with genetic algorithms.

Int. J. Prod. Res. 41, pp. 2681–2697.

Gordon O., Herrera F., Hoffmann F., Luis M., 2001.

Genetic Fuzzy Systems: Evolutionary Tuning and

Learning of Fuzzy Knowledge Base. World Scientific

Publishing Co. Pte. Ltd, U.K.

ON THE WORK-IN-PROCESS CONTROL OF PRODUCTION NETWORKS

227