
CONTACTLESS TORQUE SENSOR
Mechatronic Principle and Prototype Development for Automotive Applications
Manfred Brandl
Austriamicrosystems AG, Schloss Premstätten, Austria
Franz Haas, Reinhard Marik
FH CAMPUS 02, Department of Automation Technology, Körblergasse 126, Graz, Austria
Keywords: Torque sensor, Inductive principle, Electric steering system, Finite element method.
Abstract: In this paper fundamentals and the prototype development of a new contactless torque sensor are presented.
The whole device can be divided into a mechanical and an electromagnetic system. The prototype is
designed for the torque range of an electric power assisted steering. The basic idea is the transformation of
the shaft twist under torque load into a translational movement of the middle part of the sensor sleeve that is
measured by an inductive measuring device. An additional aspect is the low cost manufacturing and
assembling of the whole system. The interface electronics ensures high linearity and accuracy and is
therefore very suitable for this application. This new sensor concept is very robust and self-compensating
for all kinds of relative positioning tolerances ranging from temperature change to external forces.
1 INTRODUCTION
The object of this publication is to present a new
contactless torque sensor concept based on a highly
reliable inductive sensing principle for automotive
applications to overcome the drawbacks of present
solutions.
Recent automotive fuel saving and power train
techniques are requiring highly reliable but low cost
torque sensors. One example application is electric
power assisted steering system (Graßmann, 2003) to
measure input torque. Others are open or closed loop
drive train applications such as torque vectoring,
power control or power assisted bicycles.
2 TORQUE SENSOR PRINCIPLE
Torque measurement on rotating shafts leads to a
specific design requirement. The torque information
has to be transmitted in a wireless non-contact
manner from the rotating shaft to the static readout
environment. The technical solution is to pick up the
torque information on the rotating shaft and transmit
it to a stationary receiver either through electric,
magnetic or electromagnetic field.
Today’s sensing techniques are:
Strain gauge or magneto-elastic sensor on
shaft surface to measure strain in 45-degree
direction versus shaft axis;
A compliant torsion bar with optical, resistive,
inductive or magnetic (Angleviel, 2005)
measurement of the relative angle between
both ends. This principle is used in modern
electromechanical steering systems (Heißing,
2008) and fulfils the requirements of safety
and reliability.
At present torque sensors are mostly used in
industrial drive train applications, in robotics and in
bench test measurement equipment.
For this new concept the system can be divided into
two domains:
Mechanical domain;
Electromagnetic domain.
2.1 Mechanical Domain
The twist of a steel shaft under load is transformed
to an axial displacement (Jacobsen, 1944). This
effect and the core part of the torque sensor are
shown in Figure 1. The applied torque causes a shaft
55
Brandl M., Haas F. and Marik R. (2009).
CONTACTLESS TORQUE SENSOR - Mechatronic Principle and Prototype Development for Automotive Applications.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,
pages 55-61
DOI: 10.5220/0002208300550061
Copyright
c
SciTePress

twist that is induced into a specially designed sleeve.
This part, for instance made of aluminium, is
perfectly attached to the shaft at two cylindrical
faces with a constant distance. The connections of
the middle part to the outside parts represent thin
rods that translate the twist into a translational
movement (Δx) along the shaft rotation axis.
Figure 1: Sleeve with the fixation parts, middle part and
connection rods.
Possible manufacturing processes are chipping
technologies (turning and milling), powder injection
moulding or welded composite from punched parts
depending on the production volume.
2.2 Electromagnetic Domain
Two fixed ferromagnetic sleeves, one displaceable
centre sleeve and the two axial air gaps as part of the
rotor are shown in Figure 2.
Stator
Rotor
ferromagnetic
sleeves
Coils
Air gaps
displacable center
part of spring sleeve
Figure 2: Electro magnetic circuit formed by sensor rotor
and sensor stator.
The rotor forms a differential inductive half
bridge circuit (see Figure 3) with two fixed coils and
its respective ferromagnetic field concentrators as a
stator.
Figure 3: Sensor inductances and its parasitic resistances
connected in series to form a half bridge.
The stationary coils and their ferromagnetic
housings are placed concentric to the shaft in the
middle of the rotor with the two air gaps. When
torque is applied, one air gap increases and the other
one gets smaller by the same amount. The two coils
are connected in series and excited by a common
electrical signal. The reluctance ratio determines the
output voltage of the inductive half bridge. The
magnetic circuit is designed in such a way that a
significant portion of the total reluctance is
determined by the axial air gaps between the rotor
sleeves. Any differential change of air gap due to
applied torque leads to a non-balanced bridge and an
output signal linear with displacement in case of
small deflections.
Because of the symmetric arrangement of the
magnetic ring elements all air gap changes due to
shaft bending, shaft expansion or shaft compression
won’t lead to an output signal. Nor will concentricity
errors of the rotor influence the output signal. Even
axial simultaneous displacement of the entire rotor
like a bearing play will not lead to reluctance
difference in the first instance. Most important is
that also shaft rotation doesn’t affect the balance of
the electromagnetic circuit, either.
An important point is the matching of both air
gaps at zero torque. Any offset would lead to
unbalanced bridge and therefore to a temperature
drift of the sensor zero point. Also, non equal air gap
size over the circumference would lead to 2
nd
order
effects causing small output changes with angular
rotor position. Therefore it is proposed that the
ferromagnetic sleeves are separated exactly after
bonding by laser cutting.
As a conclusion it is obvious that this sensor
concept is very robust and self-compensating for all
kinds of relative positioning tolerances ranging from
temperature change, bearing play and forces applied
to the stator or rotor shaft.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
56
3 SENSOR OPTIMIZATION
This chapter describes the basic kinematical
principle and the FEM-optimization of the torque
sensor geometry (Marik, 2008). Optimization
criteria are the translational movement Δx, but also
the costs for manufacturing and assembling.
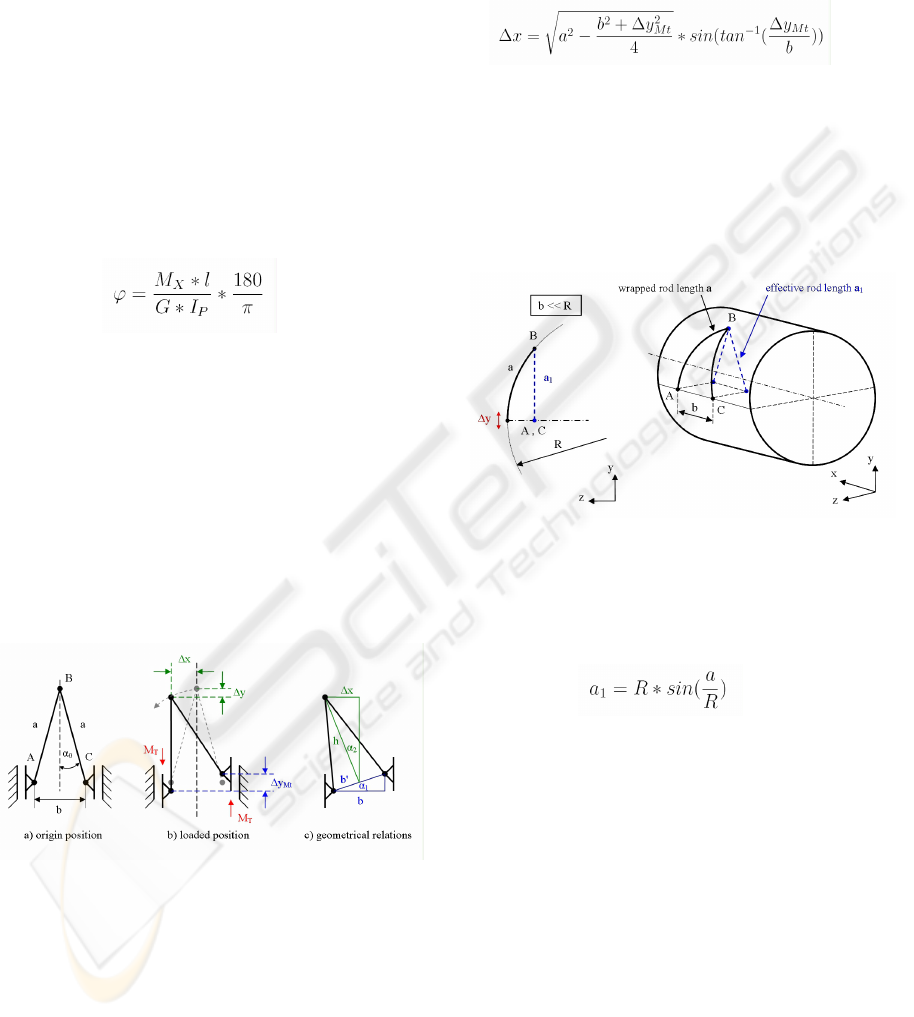
3.1 Kinematical Principle
Basically the sensibility of the torque sensor depends
on the translation ∆x which is directly linked to the
current torsion angle. The formal correlation of the
torsion angle (φ), the torque (Mx), the length of the
casing (l), the modulus of rigidity (G) and the polar
area moment (Ip) is shown in equation (1).
(1)
In most cases the shaft diameter, the external
torque, the material of the shaft and the possible
casing length are given values and cannot be
changed. Concerning the example of an 18mm
diameter steering shaft, a torsion angle φ from 0.05
to 0.06 degrees leads to a twist movement on the
shaft surface of 0.02mm. According to that point the
only way to achieve a maximum ∆x is to optimize
the design of the mechanical sleeve.
The simplified function model of the sleeve is a
two rod system with three revolute joints. Figure 4
shows the situation on a flat surface to demonstrate
the geometrical relationships more easily.
Figure 4: Simplified function model of the sleeve on a flat
surface.
Two rods with the length (a) are connected to
each other at joint (B) and to the surrounding at
joints (A) and (C) (see Figure 4a). The connection
points A and B are only moveable in the y-direction
but fixed in the x-direction. When the system gets
loaded due to a torque the points A and C move
contrarily along the y-direction (∆y
Mt) and hence the
joint B moves from its origin position along a
circular path with the radius (a) (see Figure 4b).
The geometrical relations in x-direction are
shown in Figure 4c and can be described in equation
(2).
(2)
From equation (2) it is obvious that the achieved
Δx is linear depending on the length (a) and
nonlinear to the geometric relation of Δy
M and the
width (b), the tilt angle of the system. But when the
two rod system gets wrapped around a cylinder
surface the interacting rod length will be scaled
down by the influence of the cylinder radius R as
shown in Figure 5.
Figure 5: Function model on a cylindrical surface.
Consequently to that effect the linear impact of
length (a) gets nonlinear according equation (3)
under the precondition that the distance (b) is very
short in relation to the radius (R) (b << R).
(3)
It is obvious that (a
1) has its maximum value
when (a) is the quarter of the cylinder
circumference, which is an important fact for the
geometry of the rotor rod elements.
3.2 FEM-Studies
Based on the kinematical principle the final CAD-
design has to be defined. The optimized shape of the
measuring sleeve (see Figure 1) is characterized by a
maximum Δx and a light structure with high
stiffness. Simulation helps to accelerate the
development process and to increase the quality of
the first prototype (Seiffert, 2008). The stresses in
critical regions near the revolute joint positions must
be under the fatigue limit of the chosen aluminium
alloy. The prototype sleeve is to be made as a
turning-milling part. Therefore the minimum cutting
CONTACTLESS TORQUE SENSOR - Mechatronic Principle and Prototype Development for Automotive Applications
57

tool diameter and the attainable lowness of the inner
undercuts also have to be considered.
Figure 6 shows the displacement (dx) in the
direction of the shaft axis. It is the result of a static
FEM analysis with the external torque at one side
and the fixation at the other side as model
constraints.
Figure 6: FEM result of displacement dx.
A satisfying compliance between measurement
results and simulation has been found (see Figure 7).
The measurement setup is illustrated in Figure 8.
Figure 7: Comparison between measuring and simulation.
Figure 8: Measurement setup.
In addition theoretical considerations can be
proved by reducing the dimensions of the joint
connections. Figure 9 shows the differences between
the results of the basic kinematic model and the
FEM simulations by varying rod lengths (a). Figure
10 gives an overview about changes of (dx) with
different values (b).
Figure 9: Displacement values with various rod lengths.
Figure 10: Displacement values with various values b.
4 INTERFACE ELECTRONICS
The inductive half bridge is supplemented by a
resistive voltage divider to form a Maxwell bridge.
Its output signal is amplified and converted to digital
output with high precision by an integrated data
acquisition circuit. The block diagram in Figure 11
shows the setup of the interface electronics.
Today’s semiconductor circuit design techniques
enable us to conquer new domains in precision and
ultra low drift signal conditioning unreachable just a
few years ago.
For this torque sensor an integrated data
dx
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
58

Figure 11: Block diagram of sensor interface electronics.
acquisition device was used which was specifically
designed to convert very small voltages to digital
domain with very high precision.
This data acquisition device offers two
multiplexed fully differential input channels, a
programmable gain amplifier, a 16 bit analog to
digital converter and a serial interface for device
configuration and result read-out.
Special auto zero offset architecture offers
virtually zero offset below 0.5µV and very low
noise. The analog to digital converter is of Sigma-
Delta type, an architecture which offers high
linearity without any missing codes.
The device has an integrated trim-able precision
reference and a temperature compensation for the
entire measurement path. The integrated circuit also
offers a measurement-ready signal which is used to
excite the transducer bridge with a pulsed DC
voltage in conjunction with a diode which is to
discharge the energy stored in the coils after each
applied pulse.
The second channel can be used to measure the
bridge current to compensate the temperature
coefficient of the copper coil which would otherwise
lead to a scaling error. If the digital representation of
the bridge voltage is multiplied by compensation
factor proportional to the bridge current in an
external micro controller, the final output signal can
be made independent from temperature. In that case
the coil wires are acting as a temperature sensor.
The development of the electronic system was
carried out at the Department of Automation
Technology at FH CAMPUS 02 in collaboration
with austriamicrosystems Corporation applying the
newest chip generation (Pauritsch, 2008).
5 TEST SYSTEM
Based on the presented solution a test system has
been developed that demonstrates a steering (see
Figure 12). For that purpose the demonstrator
consists of a steering shaft with torque sensor and
rotary encoders, two bearings and a steering wheel.
5.1 Torque Sensor
The torque sensor is placed in the middle of the
bearing houses. The sensor sleeve is pinned on the
18 mm diameter shaft to induce the shaft twist into
the sleeve. The stator part consists of a casing with
two coils and four ferromagnetic concentrators
forming two inductances in the range of 10mH with
CONTACTLESS TORQUE SENSOR - Mechatronic Principle and Prototype Development for Automotive Applications
59

Figure 12: Steering demo system with one torque sensor, two rotary encoders and Graphical- User-Interface (GUI) for
torque measurement.
400 windings of 0,15mm copper wire. The entire
coil arrangement is fixed by two screwed covers.
The stator has to be aligned to the axis of the
shaft carefully.
The coil wires are led through small holes and
connected with the sensor interface. The PCB is
mounted on the base plate of the demonstrator. The
steering torque can be simulated by a DC-motor or
by a special brake with a fixation screw.
5.2 Rotary Encoder
In addition to the torque measurement the steering
angle is also measured at two positions by using
Hall-sensors.
The rotary encoder (Czichos, 2008) consists of a
small magnet disc with north/south pole, which
rotates at a very short distance to the Hall-sensor-
chip. This disc is directly mounted on a small
gearwheel. The according gear consists of the pinion
gear with the magnet and a gearwheel that is fixed
on the steering shaft. The casing of the rotary
encoder is separated into two parts for easy
assembling and also includes the sensor PCB.
5.3 User Interface
The user interface software is programmed with
“Labview” and enables various types of graphical
representation of the measurement results.
5.4 Linearity Measurement
The characteristic of the new sensor is the result of
measurements within a specified torque range of
±5Nm. Figure 13 shows the sensor output signal
which is virtually linear with torque without any
hysteresis.
Figure 13: Torque sensor characteristic without any
hysteresis.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
60

6 CONCLUSIONS
A contactless torque sensor for accurate and reliable
low frequency torque measurement on a rigid
steering shaft has been introduced. The principle is
in our opinion well suited to develop a low cost
sensor product with adequate values of repeatability,
accuracy and reliability. The cost and quality targets
can be achieved, if manufacturing techniques like
laser cutting and laser welding will be utilized.
The entire mechatronic solution is based on well
known design elements which do not lead to long
term drifts of zero point and output scale. There is
virtually no hysteresis in output signal as proven by
the demonstrator design.
It has to be pointed out that the design of a final
sensor product has to consider sufficient spring
stiffness in axial direction as well as low mass for
the displaceable centre sleeve spring/mass system to
ensure insignificant displacement when the sensor is
exposed to low frequency or constant acceleration. It
has to be ensured that its first mode resonance
frequency is higher than the frequency band of
interest.
Our contribution represents a preparatory study
for any subsequent mechatronic product
development.
Due to the number of involved technical
disciplines like mechanical-, electromagnetic-,
electronic-, manufacturing- and safety engineering it
is recommended to continue the research work as an
academic project in conjunction with other
universities and industrial partners.
We are confident that as a result of such R&D-
activities a new type of mechatronic torque sensor
device with unmatched performance versus cost
ratio can be placed on the market for many
applications.
REFERENCES
Angleviel, D., Frachon, D., and Masson, G., 2006.
Development of a Contactless Hall effect torque
sensor for Electric Power Steering. MMT S.A.
Czichos, H., 2008. Mechatronik. P 217. Vieweg+Teubner
Verlag. Wiesbaden.
Graßmann, O., Henrichfreise, H., Niessen H., and
Hammel K., 2003. Variable Lenkunterstützung für
eine elektromechanische Servolenkung. 23. Tagung
“Elektronik im Kfz”. Stuttgart.
Heißing, D., Ersoy M., 2008. Fahrwerkhandbuch. pp 209-
215. Vieweg+Teubner Verlag. Wiesbaden.
Jacobsen, A.M., 1944. Electrical Dynamometer. US Patent
Application Serial No. 561,467. Los Angeles.
Marik, R., 2008. Konturoptimierung einer Messnabe.
Bachelor Thesis. FH CAMPUS 02. Graz.
Pauritsch, M., 2008. Product documentation of the sensor
interface. Graz..
Seiffert, U., Rainer G., 2008. Virtuelle Produktentstehung
für Fahrzeug und Antrieb im Kfz. pp 7-29.
Vieweg+Teubner Verlag. Wiesbaden.
CONTACTLESS TORQUE SENSOR - Mechatronic Principle and Prototype Development for Automotive Applications
61
