
APPLYING SUB-POPULATION MEMETIC ALGORITHM FOR
MULTI-OBJECTIVE SCHEDULING PROBLEMS
Yen-Wen Wang
Department of Industrial Engineering and Management, Chin Yun Tech. University
229 Chien-Hsin Rd., Taoyuan, Taiwan. R.O.C.
Chin-Yuan Fan
Department of Industrial Engineering and Management
Yuan-Ze University, Taoyuan, Taiwan, R.O.C.
Chen-Hao Liu
Department of Information Management, Kainan University
Taoyuan Taiwan, R.O.C.
Keywords: Flowshop scheduling problem, Multi-objective scheduling, Memetic Algorithm.
Abstract: Memetic Algorithm is a population-based approach for heuristic search in optimization problems. It has
shown that this mechanic performs better than traditional Genetic Algorithms for some problem. In order to
apply in the multi-objective problem, the basic local search heuristics are combined with crossover operator
in the sub-population in this research. This approach proposed is named as Sub-population with Memetic
Algorithm, which is applied to deal with multi-objective Flowshop Scheduling Problems. Besides, the
Artificial Chromosome with probability matrix will be introduced when the algorithm evolves to certain
iteration for injecting to individual to search better combination of chromosomes, this mechanism will make
faster convergent time for evolving. Compares with other three algorithms which are MGISPGA, NSGA-II
and SPEA2, the experiments result show that this algorithm possess fast convergence and average scatter of
Pareto solutions simultaneously for solving multi-objective Flowshop Scheduling Problems in test
instances.
1 INTRODUCTION
In the operations research literature, Flowshop
scheduling is one of the most well-known problems
in the area of scheduling. Flowshops are useful tools
in modeling manufacturing processes. A
permutation Flowshop is a job processing facility
which consists of several machines and jobs to be
processed on the machines. In a permutation
Flowshop all jobs follow the same machine or
processing order and job processing is not
interrupted once started. Our objective is to find a
sequence for the jobs so that the makespan or the
completion time is a minimum.
In this research, we take a close look at the
evolutionary process for a permutation Flowshop
scheduling problems and come out with the new
idea of generating artificial chromosomes to further
improve the solution quality of the genetic
algorithm. To generate artificial chromosomes, it
depends on the probability of each job at a certain
position. The idea is originated from Chang et
al.(2005) which propose a methodology to improve
Genetic Algorithms (GAs) by mining gene
structures within a set of elite chromosomes
generated in previous generations. Instead of
replacing the crossover operator and mutation
operator due to efficiency concern, the proposed
algorithm is embedded into simple GA (SGA) and
non-dominated sorting genetic algorithm-II (NSGA-
II). The probability model acquired from the elite
chromosomes will be integrated with the genetic
376
Wang Y., Fan C. and Liu C. (2009).
APPLYING SUB-POPULATION MEMETIC ALGORITHM FOR MULTI-OBJECTIVE SCHEDULING PROBLEMS.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,
pages 376-379
DOI: 10.5220/0002208603760379
Copyright
c
SciTePress

operators in generating artificial chromosomes, i.e.,
off-springs which can be applied to enhance the
efficiency of the proposed algorithm. Apart from our
previous researches, Harik (1999), Rastegar (2006),
Zhang (2005) have discussed and proved the genetic
algorithm which is based on the probability models.
For a complete review of the relative algorithms
discussed above, please refer to Larranaga (2001),
Lozano (2006), and Pelikan (2002). In most recent
works of evolutionary algorithm with probability
models, they all concentrate on solving continue
problems rather than discrete problems. There are
only few researches in applying evolutionary
algorithm with probability models to resolve discrete
problems.
2 METHODOLOGY
A new approach is developed in this research which
is called SPMA. The method is proposed to solve
Flowshop scheduling problems and will be
compared with SPGA, NSGA-II and SPEA-II.
Through literature reviews, we find that SPGA has
very good diffusivity when solving multi-objective
problems; however, as for convergence, there still
remains room for improvement. Thus, the research
tries to strengthen the solution convergence of
SPGA by mining gene structures and local search
heuristic. Except for the original mining gene
structures (Chang 2005), we called Artificail
chromosomes (AC).
2.1 Generating Artificial Chromosomes
During the evolving process of the GA, all the
chromosomes will converge slowly into certain
distribution after the final runs. If we take a close
look at the distribution of each gene in each assigned
position, we will find out that most the genes will be
converged into certain locations which means the
gene can be allocated to the position if there is a
probabilistic matrix to guide the assignment of each
gene to each position. Artificial Chromosomes (AC)
are developed according to this observation and a
dominance matrix will record this gene distribution
information. The dominance matrix is transformed
into a probability matrix to decide the next
assignment of a gene to a position. Consequently,
AC is integrated into the procedure of genetic
algorithm and it attends to improve the performance
of genetic algorithm. The primary procedure is to
collect gene information first and to use the gene
information to generate artificial chromosomes.
Before collecting the gene information, AC collects
the chromosomes whose fitness is better by
comparing the fitness value of each chromosome
with average fitness value of current population.
Then artificial chromosome is embedded into the
genetic algorithm. The detailed steps are described
in the following:
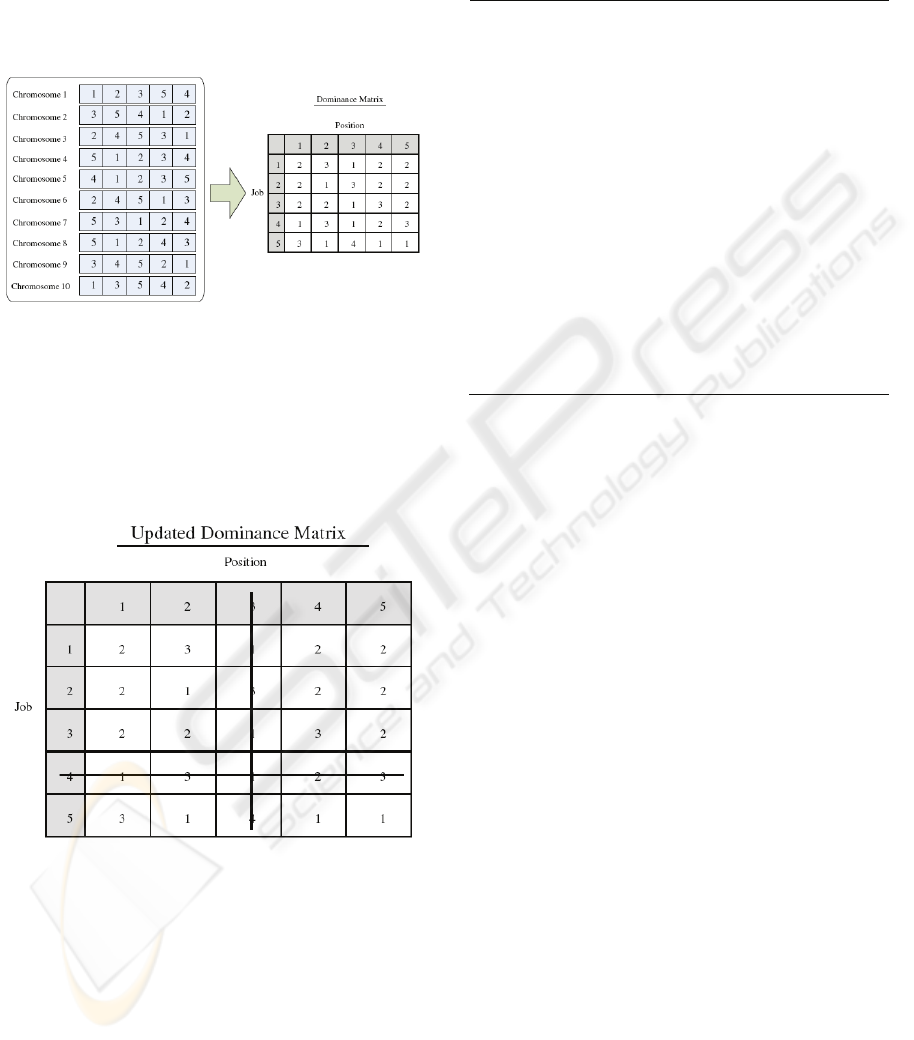
1. To convert gene information into dominance
matrix:
Before we collect gene information, selection
procedure is performed to select a set of
chromosomes. Then, for a selected chromosome,
if job i exists at position j, the frequency is added
by 1. To demonstrate the working theory of the
artificial chromosome generation procedure, a 5-
job problem is illustrated. Suppose there are ten
sequences (chromosomes) whose fitness is better
than average fitness. Then, we accumulate the
gene information from these ten chromosomes to
form a dominance matrix. As shown in the left-
hand side of Figure 1, there are two job 1, two job
2, 2 two 3, one job 4, and three job 5 on position
1. Again, there are 3 job 1, 1 job2, 2 job3, 3 job4,
and 1 job5 on position 2. The procedure will
repeat for the rest of the position. Finally, the
dominance matrix contains the gene information
from better chromosomes is illustrated in the
right-hand side of Figure 1.
2. Generate artificial chromosomes:
As soon as we collect gene information into
dominance matrix, we are going to assign jobs
onto the positions of each artificial chromosome.
The assignment sequence for every position is
assigned randomly, which is able to diversify the
artificial chromosomes. After we determine the
assignment sequence, we select one job assigned
to each position by roulette wheel selection
method based on the probability of each job on
this position. After we assign one job to a
position, the job and position in the dominance
matrix are removed. Then, the procedure
continues to select the next job until all jobs are
assigned. Assume the first job is to be assigned at
position 3 in the beginning. The frequency of each
job at position 3 is [1, 3, 1, 1, and 4] starting from
job 1 to job 5. Because the number of total
frequency is 10, the corresponding probability for
job 1 is 1/10; job 2 is 3/10, and so on. Then, we
accumulate the probability from job 1 to 5 and
roulette wheel select is able to apply this
accumulated probability. If a random probability
0.6 is generated, then job 4 is assigned to position
3.
3. Replacement strategy:
APPLYING SUB-POPULATION MEMETIC ALGORITHM FOR MULTI-OBJECTIVE SCHEDULING PROBLEMS
377
After embedding artificial chromosomes into
the population, we use l + k strategy, which
combines previous parent population and artificial
chromosomes. Then, we select better l
chromosomes from the combined population.
Consequently, better solutions are preserved to the
next generation.
Figure 1: To collect gene information and converted into a
dominance matrix.
During the assignment of each job to a specific
position, the dominance matrix will be updated
continuously. For example, after assigning job 4 at
position 3 and suppose position 2 is the next one to
be assigned. An updated dominance matrix is shown
in Figure 2.
Figure 2: The updated dominance matrix after assigning
job 4 at position 3.
Next, the probability of each job is recalculated
as well as the accumulated probability. Then, a
roulette wheel selection method will select a job
based on the probability of each job. Consequently,
the algorithm iteratively assigns jobs to vacant
positions until all jobs are assigned.
2.2 The procedure of SPMA
The detailed procedure of SPMA is shown as the
following:
(Ns is the number of sub-populations; g is the
number of generations; k is the interval number of
artificial chromosomes’ generations.)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
Initialize();
DividePopulation();
AssignWeightToEachSubGroup();
for i=1 to Iterations
for j=1 to Groups
if i % k == 0
ArtificialChromosome(j);
<GenerateArtificialChromosome(j);
LocalSearch(j);
SurvivalofThefittest(j);>
else
GeneAlgorithm(j);
<Selection(j);
Crossover(j);
Mutation(j);
LocalSearch(j);
SurvivalofThefittest (j);>
FindPareto(Groups);
UpdatePareto(Groups);
Compared with SPGA, this approach is different
in that it has the mechanism of creating AC, local
search heuristic and the sorting information of
chromosomes in each mutation is recorded for the
use of creating AC and placing them in the mating
pool for evolution. In the end,
R
D1
is a metric
which considers the convergence and diversity
simultaneously (Knowles, 2002) and it is adopted in
this research to evaluate the solution quality. Its
main concept is to calculate the shortest distance
between each solution in the Pareto-Solution set and
the set to be compared with, and then calculate the
mean value. The smaller
R
D1 is the better.
3 EXPERIMENTAL TESTS
The research uses the Flowshop scheduling case
study by Ishibuchi (2003) in which four types were
included in the bi-objective flow-shop problems;
they were 20 jobs in 20 machines, 40 jobs in 20
machines, 60 jobs in 20 machines and 80 jobs in 20
machines. Two objectives are the total completion
time (Cmax) and maximum tardiness (Tmax). The
processing and completion time are the same as used
in Ishibuchi et al. (2003). The experimental results
will be compared with those of SPGA, NSGA-II and
SPEA-II. The testing result of this sample problem is
depicted in Table 1 and Figure 3. It is obvious that
SPMA performs better in the small and medium size
problem (job = 20, 40, 60). And it deserve to be
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
378
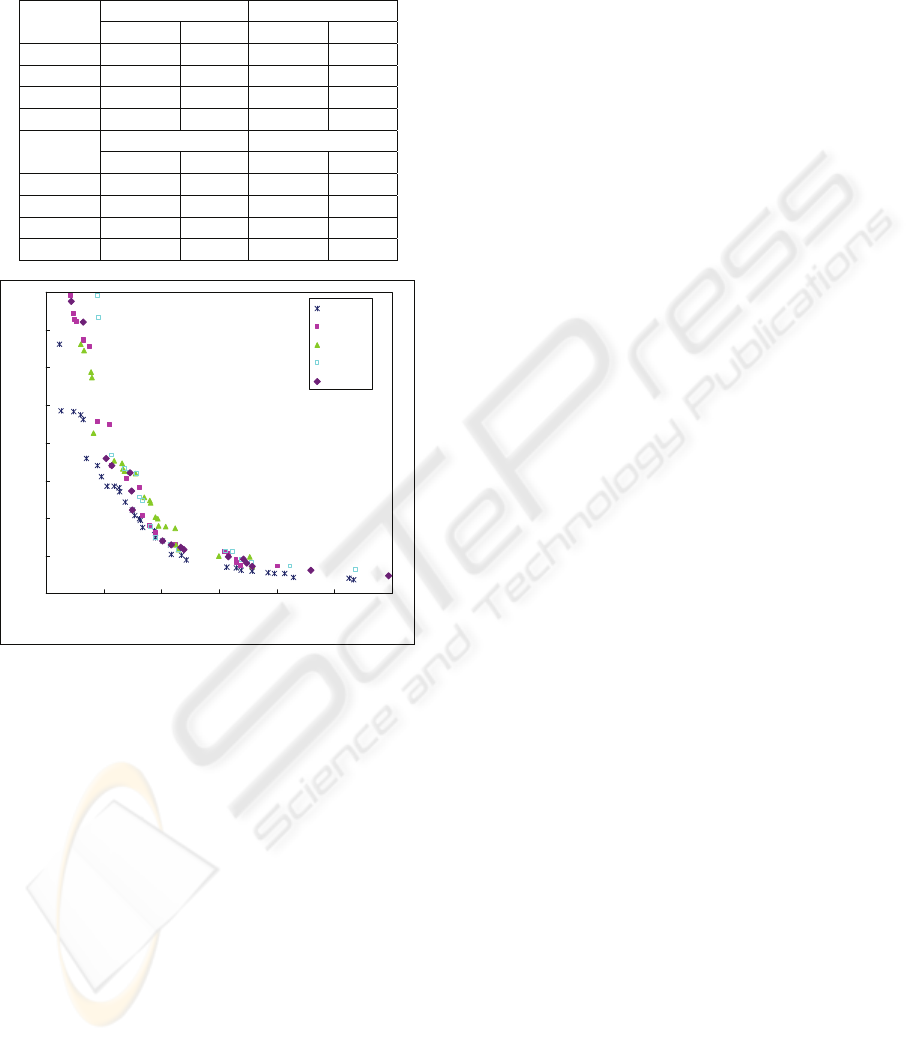
mentioned is the Std. of SPMA is much less than
other models.
Table 1: The algorithm comparison with other methods.
Instance
(job)
NSGA II SPEA II
Ave. Std. Ave. Std.
20 43.05 14.42 37.35 14.22
40 146.36 28.71 138.6* 19.9
60 321.12 57.86 291.02 52.78
80 424.96 93.92 394.14 63.79
Instance
(job)
SPGA SPMA
Ave. Std. Ave. Std.
20 38.62 9.44 22.46* 8.89
40 146.21 21.09 142.40 20.03
60 341.86 94.15 261.24* 34.49
80 344.45* 99.12 515.34 75.72
0
100
200
300
400
500
600
700
800
2250 2300 2350 2400 2450 2500 2550
Cmax
Tmax
Reference
NSGAII
SPEAII
MGISPGA
SPMA
Figure 3: The plot of algorithms with reference Pareto set
of SPMA.
According to the above-mentioned four testing
results, we find that when solving more complex
problems, it is harder to find the improving
effectiveness of SPMA. Along with the increasing
number of jobs, the problems become more complex
and thus the improving effectiveness of SPMA can’t
be obviously noticed.
4 CONCLUSIONS
Through this study, we can verify that by combining
AC and local search heuristic with SPGA, multi-
objective scheduling problems can be solved more
effectively, especially in the small and medium size
problem. In the future, SPMA can be further
extended to three objectives or multidimensional
continuous problems. And the procedures of SPMA
might be improved to deal with large size problem.
Further investigation will be carried out to
examine whether it is possible to generate elite
chromosomes through better mining algorithms. It is
also suggested that different objectives of Flowshop
scheduling problems can be further tested such as
the arrival time of job is considered, and those with
more complex requirements such as sequence
dependent setup times.
REFERENCES
Chang, P. C., Chen, S. H., and Lin, K. L., 2005, Two
phase subpopulation genetic algorithm for parallel
machine scheduling problem, Expert Systems with
Applications, 29(3), 705–712.
Harik, G.R., Lobo, F.G., and Goldberg, D.E., 1999, The
compact genetic algorithm, IEEE Transactions of
Evolution Computing, 3 (4), 287–297.
Ishibuchi, H., Yoshida, T. and Murata, T., 2003, Balance
between Genetic Search and Local Search in Memetic
Algorithms for Multi-objective Permutation Flowshop
Scheduling, IEEE Trans on Evolutionary
Computation, 7(2), 204-223.
Larranaga, P., and Lozano, J.A., 2001, Estimation of
Distribution Algorithms: A New Tool for
Evolutionary Computation, Kluwer, Norwell.
Lozano, J.A., Larranaga, P., Inza, I., and Bengoetxea, E.,
2006, Towards a New Evolutionary Computation,
Springer.
Pelikan, M., Goldberg, D.E., and Lobo, F.G., 2002, A
survey of optimization by building and using
probabilistic models, Computational Optimization
and Applications, 21 (1), 5–20.
Rastegar, R., and Hariri, A., 2006, A step forward in
studying the compact genetic algorithm, IEEE
Transactions of Evolution Computing, 14 (3), 277–
289.
Zhang, Q., Sun, J., and Tsang, E., 2005, An evolutionary
algorithm with guided mutation for the maximum
clique problem, Evolutionary of Computing, 9 (2), 192
–200.
APPLYING SUB-POPULATION MEMETIC ALGORITHM FOR MULTI-OBJECTIVE SCHEDULING PROBLEMS
379
