OBSTACLE DETECTION USING STRUCTURED BACKGROUND

Ghaida Al Zeer, Adnan Abou Nabout and Bernd Tibken

Chair of Automatic Control, Faculty of Electrical, Information and Media Engineering

University of Wuppertal, Rainer-Gruenter-Str. 21, 42119 Wuppertal, Germany

Keywords: Image Processing, Mobile Robotics, Path Planning, Obstacle Detection.

Abstract: The paper presents an obstacle detection method for mobile robots using a structured background. This

method is based on differences of appearance between obstacles and the background in the camera images.

The basic idea is to cover the ground of the workspace with a known structure. If part of this structure is

obscured, this can be detected and indicates the existence of an obstacle. The method uses a reference

symbol, chosen to exhibit certain features, to construct a reference image of the structured background. To

detect possible obstacles we calculate the Fourier descriptors (FD) of all contours included in a given image

and compare them with those of the stored reference symbol. This enables us to recognize all reference

symbols which are not obscured by obstacles. We then determine the positions and dimensions of all

existing obstacles by calculating the occupied symbol areas. The method is implemented as part of a robot-

vision system for fully automated stockkeeping. In this paper the results are shown using a MATLAB

implementation.

1 INTRODUCTION

Obstacle detection is an important and essential task

in a system with mobile robots (Al Zeer, Nabout and

Tibken, 2006) and (Al Zeer, Nabout and Tibken,

2007). The method of detection depends on the

available information about the obstacles and their

environment.

There are various methods of obstacle detection,

based on different approaches (Simmons, 1996) and

(Sabe, Fukuch, Gutmann, Ohashi, Kawamoto and

Yoshigahara, 2004). Two different types of

strategies are distinguished. The first strategy is

called range-based obstacle detection. This method

is based on the measurement of the distance between

the obstacle and an implemented sensor, such as an

IR-Distance Sensor. The second method is called

appearance-based obstacle detection, in which the

obstacles, e.g. in a color picture, are separated from

the background and classified using their appearance

properties (Ulrich and Nourbakhsh, 2000).

Within our work an extended appearance-based

method for obstacle detection has been developed,

which does not use the appearance of an obstacle,

but the appearance of the background. This method,

obstacle detection using structure background, was

developed for our robot-vision system (Al Zeer,

Nabout and Tibken, 2007) and allows a reliable

detection and localization of obstacles. Grayscale

images are available as part of a robot-vision system.

These grayscale images are acquired by a camera

system mounted on the ceiling of the workspace

area. Therefore the calculation of the obstacle

positions will be carried out by image evaluation.

Objects in the workspace at the time of image

acquisition are considered as static obstacles and

they are taken into account in the calculation of

collision-free routes. Objects that inter the

workspace after the image acquisition are considered

as dynamic obstacles (Borenstein and Koren 1990).

These obstacles can be detected by the distance

sensor which is mounted on the vehicle.

Encountering a dynamic obstacle causes the vehicle

to stop immediately and to provoke a re-imaging to

calculate a new route. Several implementations of

the new method will be described in detail and then

their realization will be further illustrated.

The paper consists of four sections. In section 2

the principle of the method “obstacle detection using

structured background” is explained. Section 3 is

concerned with the selection of a suitable reference

symbol. In section 4 some results related to the

MATLAB implementation are shown and discussed.

439

Al Zeer G., Nabout A. and Tibken B. (2009).

OBSTACLE DETECTION USING STRUCTURED BACKGROUND.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 439-444

DOI: 10.5220/0002209004390444

 SciTePress

2 OBSTACLE DETECTION

The basic idea of this method is to cover of the

ground in the workspace with a known structure. If

part of this structure is obscured by an obstacle, this

can be detected. The structure can be generated by

distributing reference symbols in a regular pattern in

the workspace of the mobile robot. The distribution

of symbols results in a regular and known pattern of

contours in every picture of the workspace. Thus,

the distribution of the center positions for the

reference symbols comprises a matrix structure,

similar to the pixel matrix of a bitmapped image.

The use of a symbol pattern as reference feature

of the ground leads to an extension of the conceptual

specifications of the developed robot-vision system.

The implementation of a new strategy of obstacle

detection in the robot-vision system was necessary,

because it was observed that a guaranteed

identification of obstacles through direct detection of

objects is not possible because of lighting errors.

The condition that the ground has to be covered with

a symbol pattern is not an especially unrealistic

burden, e.g. in the case of automated stockkeeping.

To cover the floor of a warehouse with custom-

patterned tiles, painted- or pasted- on symbols is a

relatively simple requirement that does not involve a

great effort or a high cost. Moreover, in the case of a

robot-vision system, this requirement does not

violate the principles or change the basic idea of the

system.

To verify the results, using the robot-vision

system, the extended method was implemented in

Matlab and was tested under real conditions. Only

common Matlab functions were used in the

implementation. The obstacle detection using

structure background is based on the following

assumptions:

 First, an appropriate symbol pattern has to be

applied to the workspace floor. The symbol

used to generate the pattern must be suitable

for accurate detection. The shapes of the

symbol must differ greatly from the shapes of

expected objects and also from possible

shapes caused by noise and other errors.

 All symbols must be identical, i.e. they all

have to be the same shape and size, and they

must be arranged in a regular pattern with pre-

defined distances to each other.

 The symbols must be large enough for the

camera to render their shape and contours with

sufficient accuracy. This depends on the

resolution of the camera used and the distance

between camera and ground.

 The symbols should not have reflective

surfaces, so they will not cause reflection

noise under bright lighting.

In order for the symbols to comprise a regular

pattern on the ground, they have to be applied so that

their centers form a regular grid, i.e. the distance

between the centers of the symbols must be equal. In

the following the individual steps of the newly

developed method will be described in detail.

2.1 Creating a Reference Symbol

The reference symbol is used as a basis of

comparison for the detection system, so its Fourier

descriptors (FDs) are detected and saved (Nabout,

1993).

Figure 1 shows an example for such a symbol.

Here "h" is the height, "b" the width, and "c" the

center (center of area) of the symbol. The symbol

orientation is chosen in suitable way to cover the

maximum area of the workspace.

Figure 1: Reference symbol.

The center of gravity of the symbol area can be

calculated according to the following general Eq. (1)

(Nabout, 1993)

∑

∫

∑

∫

dxy

dxyx

(1)

Here,

(

)

Y,X

are the coordinates of the center

of the symbol, whose contours were approximated

by a polygon with n vertices.

The contour features of the symbol are computed

using the contour extraction methods described in

(OKE) (Nabout, 1993). Consequently, the original

grayscale image is first converted to a binary image.

Then the contours of the reference symbol are

extracted using the OKE method. Freeman-code is

used to describe the contours (cf. Figure 2 and

Figure 3).

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

440

Figure 2: Freeman-Code.

Figure 3: Contours of the

reference symbol.

The OKE method consists of the following steps:

1. Segmentation of the image into overlapping

2*2 or 4*4 windows.

2. Evaluation of these windows according to the

extraction rules in time with the image sample

rate (extraction of basic contour elements).

3. Sorting of the contour elements to generate

closed contours.

For the reference symbol used here (Fig. 3), the

following Freeman chain was obtained using the

MATLAB implementation.

The starting point of the Freeman-chain is in this

example (86, 10). The extracted contour is shown in

figure 3.

To approximate the contour of the reference

symbol the KKA method (cf. Nabout) is used. The

KKA method is carried out as follows:

1. Segmentation of the chain of contour elements

into partial sequences that satisfy certain

conditions.

2. Detection of noise chains and merging them

with neighboring chains.

3. Sorting of partial chains, approximation of

curved contour parts.

After these steps, the FDs of the reference

symbol are calculated by a Fourier-analysis and are

saved in a data structure. Fig. 4 shows the symbol

after contour approximation.

Figure 4: The approximated contour of the symbol of

Fig.1.

2.2 Creation of a Reference Image

To create a reference image, the workspace floor is

covered with symbols forming a grid structure as

described above. Then an image of the empty

workspace without obstacles is acquired (Figure 5).

Figure 5: Workspace floor with reference symbols.

The reference image should be created under real

conditions. The acquisition parameters are set so that

all the symbols in the picture are completely visible.

Since a camera-acquired image always contains

other contours in addition to the symbols (noise,

errors, etc.), as a first step all the contours in the

picture are extracted and approximated using the

OKE and KKA-methods and saved in the form of

polygonal approximations. To remove the contours

created by noise we adopt a length filter using an

upper and lower threshold for the contour length.

Subsequently, the FDs and centers of area gravity

for the symbol polygons are computed. In our

example, the reference image contains 48 symbols.

By comparing the FDs of the extracted polygon with

the FDs of the reference symbol, all existing

symbols in the reference image can be detected.

Their centers then determine the grid structure

(Figure 6).

[ 47, 45

146, 45

247, 45

346, 45

445, 45

544, 45

644, 45

744, 45

47, 138

744, 138

47, 229

744, 229

47, 322

744, 322

47, 413

744, 413

47, 506

744, 506]

Figure 6: Coordinates of center of area gravity in reference

image with 8*6 symbols.

00000066656666666566666654444445444455665665666656666666

66666666666666766667666766764544444445444222222222222222

22221222221222212221223556556556565665656656665666566666

65666664445444445432222221222122121212121211235555555556

55655565655656565665444444544444542222122221222210101010

10110110110111111111113455455454545454454444454434221222

22122001000000001000100010010010101010110110113454454445

44445444444454444444444444443222122222222007007000070000

70000000000000000000100001000101012222221222220000100000

001

OBSTACLE DETECTION USING STRUCTURED BACKGROUND

441

In our case, a grid with 8*6 symbols is

detected. Since the identification of the symbols by

comparison the shape of the extracted contours with

the shape of the reference symbol is the key to a

reliable detection of all symbols, it is necessary to

use a reference symbol whose shape (represented

through its FDs) differs greatly from those of other

occurring objects or possible noise. To choose the

reference symbol as a circle, for example, would

result in confusion with all circular contours that

arise due to lighting errors. Such a reference symbol

is not suited for the present application.

For this reason, the following strategy to select

a suitable reference symbol was used in this work.

3 SELECTION OF A SUITABLE

REFERENCE SYMBOL

Within this work, a total of 30 symbols were

investigated in order to select the most suitable

symbol for generating the grid structure. Figure 7

shows 10 of those symbols.

(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)

Figure 7: Some representatives of the symbols considered

for the generation of a symbol pattern.

The goal here is to find a symbol which gives

the smallest confusion risk with other contours that

may occur. For this reason, the FDs of all considered

symbols were calculated and compared using the

minimum distance method (Nabout, 1993). Figure 8

shows for example the first 20 FDs of the above

given symbols in a graphical comparison.

Figure 8: The first 20 FDs for the symbols of Fig.7.

The Euclidean distances 



between every two

symbols were calculated, according to Eq. (2).











A



k1

;,



1,…,30

(2)





: Euclidean distance between object i and j

: Number of Fourier descriptors





,



: Amplitude spectrum of object contour i, j

The most suitable symbol, with the smallest

confusion risk, is that one which fulfills the

following three conditions:

1. The chosen symbol must have big distances

to all other symbols. This is fulfilled for that

symbol i with the maximum mean value 





of the Euclidean distances d



,:1,…,30.

2. The symbol must have approximately equal

distances to all other symbols. This is

fulfilled for that symbol i with the minimum

variance v

of the Euclidean distances.

3. The chosen symbol must have partially

regular contour rather than irregular to

contrast to noise contours.

The means 





and the variance v

are determined

for every symbol i according to Eq. (3).









d

j1



M1

d

d





j1

(3)

Here, M is the number of considered symbols.

Finally, the symbol i with the maximum mean

value and the minimum variance is selected

according to Eq. (4).





argmin







(4)

To fulfill the third condition we calculated all

values











and sorted them according to their values

from small to large in a list (L). Then we chose the

first symbol in the list (symbol 2) which shows

partially regular contour shape. The following two

Figures show the mean value and the variance for

the objects of Fig.7.

0,00

1,00

2,00

1234567891011121314151617181920

1 2 3 4 5 6 7 8 9 10

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

442

Figure 9: Mean for each symbol (10 symbols).

Figure 10: Standard variance for each symbol (10

symbols).

4 DETECTION OF OBSTACLES

To detect the obstacles, first a picture of the

workspace is taken. This picture contains the

reference symbols on the structured floor, as well as

a certain number of obstacles. Figure 11 shows an

image with simulated obstacles.

Figure 11: Reference image with obstacles.

To evaluate this image, the following steps were

executed:

1. Contour extraction using OKE method

2. Contour approximation using KKA method

3. Computation of FDs

4. Determination of the centers of all detected

reference symbols in the image.

After performing these steps and comparing the

FDs to those of the reference symbols by the

minimum distance method we received for the given

example 35 detected reference symbols. The

detection occurs, if the computed minimum distance

value between a considered object and the reference

symbol is smaller than a specified threshold. In our

case, the threshold was determined a priori and set

to the value 0.5.

If the minimum distance is greater than this

threshold, the considered object is designated as an

obstacle. To locate the positions and sizes of existing

obstacles the centers of found symbols in the current

image are compared with the centers of the symbols

in the reference image. The centers of the detected

symbols and the centers of the symbols in the

reference image must be identical, within a certain

tolerance value. For our example, we obtain the

following results (Fig. 12).

Figure 12: Binary image with numbered objects.

Here, there are 13 symbols obscured by

obstacles, whose centers are also known.

The calculation of the positions and sizes of the

obstacles to determine the region occupancy is

illustrated in the following section.

4.1 Mapping the Obstacles into the

Workspace

In an X-Y coordinate system, whose origin is

situated in the upper left corner of the workspace (cf.

Fig.11), each symbol S



is represented by the

position of its center x



. For two adjacent

symbols on a horizontal line, the distance between

0,0

1,0

2,0

3,0

4,0

5,0

12345678910

Mean value

0,0

0,5

1,0

12345678910

Variance

OBSTACLE DETECTION USING STRUCTURED BACKGROUND

443

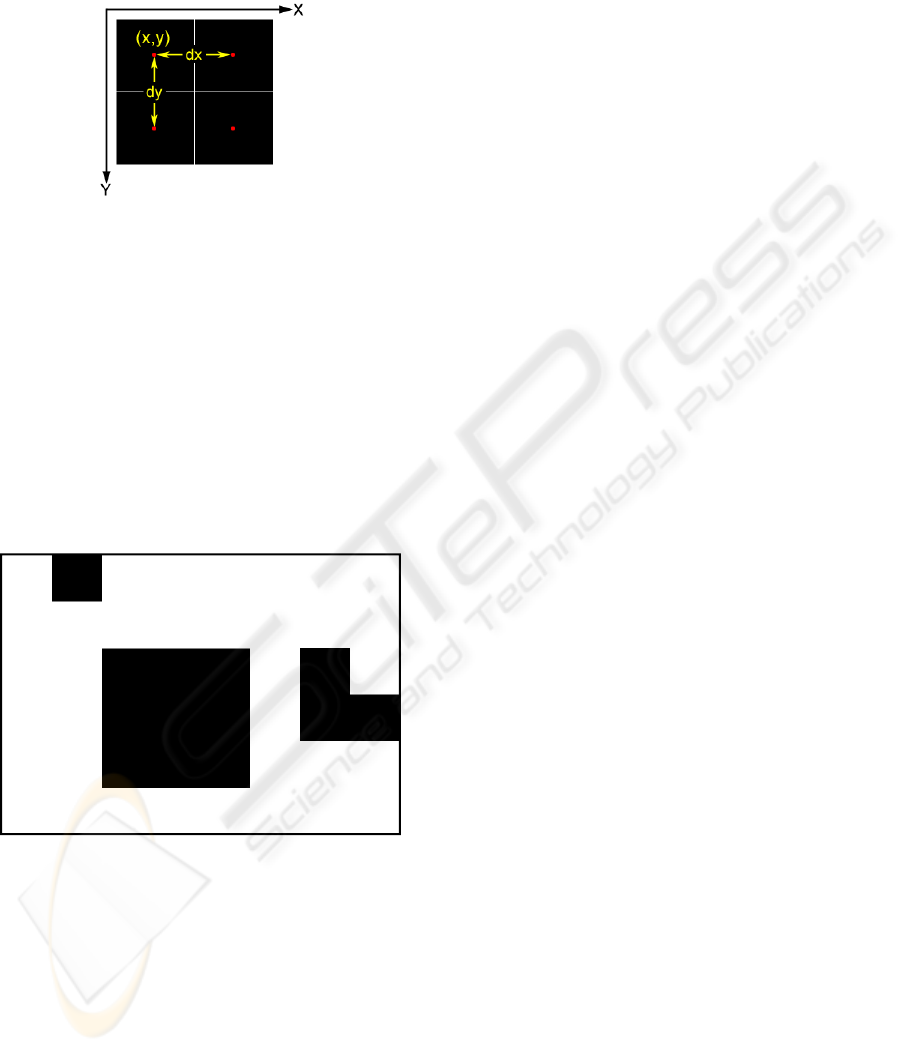
the centers of these two symbols is dx. Similarly, for

two adjacent symbols, which are arranged vertically,

it is dy.

Figure 13: Center of a macro pixel with horizontal and

vertical distance to its neighbours.

In order to detect the positions and size of the

existing obstacles in the workspace, a binary image

with the same resolution as the original grayscale

image is generated. The image is then divided into

regular  blocks, where M is the number of

columns and N is the number of rows in the symbol

grid. All pixels within one block are assigned as "0"

(black), if the symbol represented by this block is

obscured by an obstacle, otherwise, the pixels are

assigned the value "1" (white). Figure 14 shows the

binary image generated for the example of Figure11.

Figure 14: Binary image showing occupancy of obstacles.

As the picture shows, there are three black areas,

which represent the positions of the obstacles. In

order to determine the size of the obstacles, the

contours of the areas are described as polygons. For

these polygons the Minimum Area Rectangles of the

obstacle regions (MAR) are then calculated

(Al Zeer, Nabout and Tibken, 2008). These regions

represent the workspace area occupied by the

present obstacles.

5 CONCLUSIONS

With the obstacle detection method presented here,

it is possible to detect existing obstacles in the

workspace of mobile robots. This method uses

grayscale images and a specially chosen reference

symbol. The results show that symbols with

irregular contour shape are not qualified to be used

as reference symbol, since the recognition process

leads to confusion with possible lighting errors and

other noise. The paper shows how to choose a good

reference symbol using a mathematical formula.

The method was developed for the detection of

obstacles in a robot vision system which is part of a

fully automated stockkeeping application. In this

context the results of the obstacle detection

described in this paper were also used for path

planning using auxiliary corners.

REFERENCES

Al Zeer, G., Nabout, A., Tibken, B., Path Planning for

Mobile Robots by Means of Approximate Routes,

2007 IEEE International Conference on Control and

Automation, Guangzhou, CHINA, May 30 to June 1,

2007, pp. 2468-2473.

Al Zeer G., Nabout, A., Tibken, B., Hindernisvermeidung

für Mobile Roboter mittels Ausweichecken, 52nd

Internationales Wissenschaftliches Kolloquium,

Technische Universität Ilmenau, 10.–13. Sep. 2007,

pp. 437-442.

Al Zeer, G., Nabout, A., Tibken, B., Extended Method for

Path Planning Using Auxiliary Corners, the 3rd IEEE

International Conference on Information &

Communication Technologies: from Theory to

Application, ICTTA'08, 7-11 April 2008, Damascus –

Syria.

Borenstein, J., Koren, Y., Real time obstacle avoidance for

fast mobile robots in cluttered environments. IEEE

Conf. Robotics and Automation, pp. 572-577, 1990.

Nabout A., Modulares Konzept und Methodik zur

wissensbasierten Erkennung komplexer Objekte in

CAQ-Anwendungen, 1993.

Simmons. R., The Curvature-Velocity Method for Local

Obstacle Avoidance. In Proc. IEEE Conf. Robotics

and Automation, 1996.

Sabe, K., Fukuch, M., Gutmann, J., Ohashi, T., Kawamoto

K., Yoshigahara, T., Obstacle Avoidance and Path

Planning for Humanoid Robots using Stereo

Vision.Proceedings of the International Conf. on

Robotics and Automation, ICRA'04, New Orleans,

April 2004.

Ulrich, I., Nourbakhsh, I., Appearance-Based Obstacle

Detection with Monocular Color Vision, Proceedings

of the AAAI National Conference on Artificial

Intelligence, Austin, TX, July/August 2000.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

444