THREEDIMENSIONAL TRACKING USING OBJECT DEFOCUS

In Twodimensional Scanning Electron Microscope Images

Christian Dahmen

Division Microrobotics and Control Engineering, University of Oldenburg, Oldenburg, Germany

Keywords:

Image processing, Object tracking, Depth estimation, Focus analysis.

Abstract:

This paper proposes a tracking algorithm for the extraction of threedimensional position data from SEM im-

ages. An algorithm based on active contours with region-based minimization is chosen as basis for twodi-

mensional tracking. This algorithm is then augmented by the incorporation of defocus analysis to estimate

the out-of-focus displacement of the object. To solve the ambiguity of the out-of-focus displacement, the

astigmatism of the SEM images is used. The separate calculation of variances for the rows and columns of

the image enables a successful direction estimation. With the information on the direction, the out-of-focus

displacement and the working distance of the acquired image, the distance of the object to the electron gun can

be calculated. In combination with the twodimensional part of the tracking, a full threedimensional coordinate

set is generated. The approach is tested and evaluated using a positioning setup and the principal feasibility is

shown.

1 INTRODUCTION

The SEM has been widely used as a imaging tool

for the automated handling of micro- and nanoscale

objects (see e.g. (Fatikow, 2007)). While there

have been many manipulations executed manually,

and with the necessary experience these manipula-

tions have a high success rate, fully automated han-

dling and manipulation of micro- or even nanoscale

objects in the SEM still is very rarely encountered.

The problems which have to be solved are manifold

and not easy to handle. Integrated sensors in the actu-

ators or the setup may deliver some information about

the positions of end-effectors and tools, and enable

estimates about the position of objects to be manip-

ulated. The real actual position information of ob-

jects or tools though is difﬁcult to recover from this

data, because of various factors like thermal drift, play

or object interactions on the nanoscale. A speciﬁc

requirement for non-teleoperated processes is there-

fore the need for sensor feedback generation based

on SEM images. The SEM is the only sensor which

may deliver an overview over the whole scene, en-

abling the extraction of the positions of most or all

objects engaged in the manipulation. Only the SEM

determines these positions in a common coordinate

system, which makes it possible to evaluate relative

distances between the objects. One problem which is

crucial for the success of any automation approach is

the missing information about the position of objects

in z-direction, which means orthogonal to the image

plane. An example image illustrating the problem is

shown in ﬁgure 1.

Figure 1: A screenshot showing two objects having differ-

ent z-positions. One object is a silicon nanowire, the other

a deformed STM tip. The distance between the objects in

z-direction is not immediately visible.

Dahmen C. (2009).

THREEDIMENSIONAL TRACKING USING OBJECT DEFOCUS - In Twodimensional Scanning Electron Microscope Images.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 72-78

DOI: 10.5220/0002209200720078

 SciTePress

2 STATE OF THE ART

Different algorithms have been described in the lit-

erature extracting the twodimensional position of ob-

jects from SEM images for automation purposes. The

performance of these algorithms is good, making

ﬁrst simple automation scenarios possible. The ap-

proaches used for twodimensional tracking on SEM

images and their possible extensions to 3D-tracking

will be summarized in the following.

One of the ﬁrst and most simple approaches used

template matching as the basis of the algorithm (Siev-

ers and Fatikow, 2006). A template image is extracted

or loaded which contains the object to be tracked. The

template image is then cross-correlated with a search

area in the input image. The maximum value of the re-

sulting array is in the place where the template is most

likely to be found. Due to the use of cross correlation,

this approach is very robust against additive noise,

which is an advantage especially for fast scanned

SEM images. Problems of this approach are that the

algorithm is sensitive against certain changes in the

object appearance which may occur during handling

processes. Examples for these appearance changes

are rotation of the object, scaling of the object due to

magniﬁcation changes and partial occlusion by other

objects in the setup. Removing these weaknesses for

this method comes with increased computational ef-

fort so that a fast enough calculation is not always

possible. Extraction of the z-position is not featured

and cannot easily be added.

If instead of a template image a CAD model of

the object is available, it is possible to use rigid body

models to track the object in the SEM image (Kra-

tochvil et al., 2007). The implementation uses mea-

surement lines orthogonal to the model edges and

tries to ﬁt the model to visible edges in the image.

Model edges which should be invisible are identiﬁed

and not used for the pose estimation. Though edge de-

tection is difﬁcult in noisy SEM images, the approach

yields good results using advanced techniques for dis-

carding or outweighting false edges and through the

high number of measurement lines used. When three-

dimensional CAD-models are used, it is possible to

recover the threedimensional pose including in-plane

and out-of-plane rotations, except the z-position. The

extension for true threedimensional tracking relies on

a model of the SEM image projection to yield the z-

component of the position. This seems to be working

for low magniﬁcations.

Another possibility is the use of active contours

or snakes (for details about this concept see (Blake

and Isard, 2000)), which do not rely on much pre-

existing knowledge about the object. Active contours

are parametrized curves in twodimensional space, that

means in the image plane. After coarse initialization

the contour is evolving to segment the object from the

scene. The contours are coupled with an energy func-

tion dependent on their shape or appearance, and on

the image data. This energy function is being mini-

mized by moving contour points or the contour as a

whole. The part dependent on the contour is called

internal energy, the part dependent on the image data

is the external energy. In the original formulation,

the external energy function was deﬁned to be depen-

dent on the distance of the contour from edges in the

image, as explained in (Kass et al., 1988). For the

use with noisy SEM images, a region-based approach

(see (Sievers, 2006) and (Sievers, 2007)) has shown

to be useful. The external energy function here is de-

pendent on the region statistics and the noise charac-

teristics of the imaging source. The goal is to max-

imize the compound probability of the enclosed re-

gion. This approach has proven to be very robust to

additive noise, and is inherently robust against scaling

and rotation. If the contour minimization is restricted

to the euclidean transform space, robustness against

partial occlusion is added. Due to the model-free na-

ture of this approach, threedimensional tracking is not

immediately possible, but the coupling with focus-

based methods is principally possible and shows ﬁrst

promising results in the SEM.

In this paper, the last tracking approach is taken

as a basis, and extended to use defocus analysis for

depth estimation. The extracted information is only

the z-position of the tracked object, without any struc-

tural information about the object. For the recovery of

threedimensional structure of objects, different meth-

ods may be used (see e.g. (Fernandez et al., 2006) or

ahnisch and Fatikow, 2007)).

3 PRINCIPLE

The principle of the twodimensional tracking has

been explained already in (Sievers, 2006). The impor-

tant aspect is that the active contour algorithm does

not only deliver the position information of the ob-

ject, but at the same time calculates a segmentation

of the object from the rest of the scene. This enables

further analysis of the enclosed object.

Due to the working principle of the SEM, only a

certain range around the set working distance is de-

picted sharp. Though this range is quite big in com-

parison to optical microscopes, defocusing is still evi-

dent, as can be seen in ﬁgure 2. The defocusing in the

SEM has been used already in (Eichhorn et al., 2008)

to determine the z-position of objects by generating

THREEDIMENSIONAL TRACKING USING OBJECT DEFOCUS - In Twodimensional Scanning Electron Microscope

Images

a sharpness curve over a certain working distance

range. One drawback is the amount of time needed

to obtain this image sequence and therefore also the

disability to monitor dynamic processes. But by ana-

lyzing the sharpness of the object which is of interest,

it is also possible to directly conclude to the out-of-

focus displacement of the object, as has been recently

demonstrated for the SEM in (Dahmen, 2008).

Figure 2: Comparison of object in focus and out of focus.

The sharpness measure used here is the grey-level

variance

(I, A(C)) =

A(C)

∑

p∈C

I(p) −

I(A(C)) (1)

with

I(A(C)) =

A(C)

∑

p∈A(C)

I(p)), (2)

and C the contour, A(C) the enclosed area and I

the image.

For the object enclosed by the contour this means

(I(W D), A(C)) = Max ⇒ z(Ob ject) = W D (3)

with the working distance W D and the z-position

of the Object enclosed by the contour z(Ob ject).

One problem which persists after this analysis still

is that the out-of-focus displacement turns out to be

ambiguous. Two possibilities exist for the solution of

this problem, one assuming that the object is nearer

than the working distance, the other assuming that

the object is further away. This is a situation which

is not optimal for automation purposes. Though in

some cases the correct solution may be determined

by the setup and context knowledge, it is desirable to

determine the solution without additional information

apart from the image. For this case, a normally unde-

sired effect in SEM imaging may be taken advantage

of.

During normal use of the SEM, astigmatism is

something that is being diminished or removed by

astigmatism correction. Astigmatism in the SEM

leads to blurry images for the user. An important

property of astigmatism is that the sharpness is direc-

tion dependent. The focal points are different for two

perpendicular directions, as can be seen in ﬁgure 3. If

we name the two perpendicular directions w

and w

W D

6= W D

(4)

Figure 3: Astigmatism in the SEM, left and right slightly

out of focus, middle focused.

To take advantage of this, we calculate addition-

ally to the grey level variance of the image the grey

level variance of the rows and columns separately by

using

(I, A(C)) =

∑

A(C)

(y)

∑

p(x,y)∈C

I(p) −

I(A(C), y)

(5)

with

I(A(C), y) =

A(C)

(y)

∑

p(x,y)∈A(C)

I(p)) (6)

and

(I, A(C)) =

∑

A(C)

(x)

∑

p(x,y)∈C

I(p) −

I(A(C), x)

(7)

with

I(A(C), x) =

A(C)

(x)

∑

p(x,y)∈A(C)

I(p)) (8)

and C the contour, A(C) the enclosed area and I the

image.

The two values are normalized to their maximum,

which is determined during the initialization phase

(see section 4):

(I, A(C)) =

(I, A(C))

max(σ

(I, A(C)))

(9)

and

(I, A(C)) =

(I, A(C))

max(σ

(I, A(C)))

(10)

In this case we expect a working distance sweep

to generate two slightly displaced curves like depicted

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

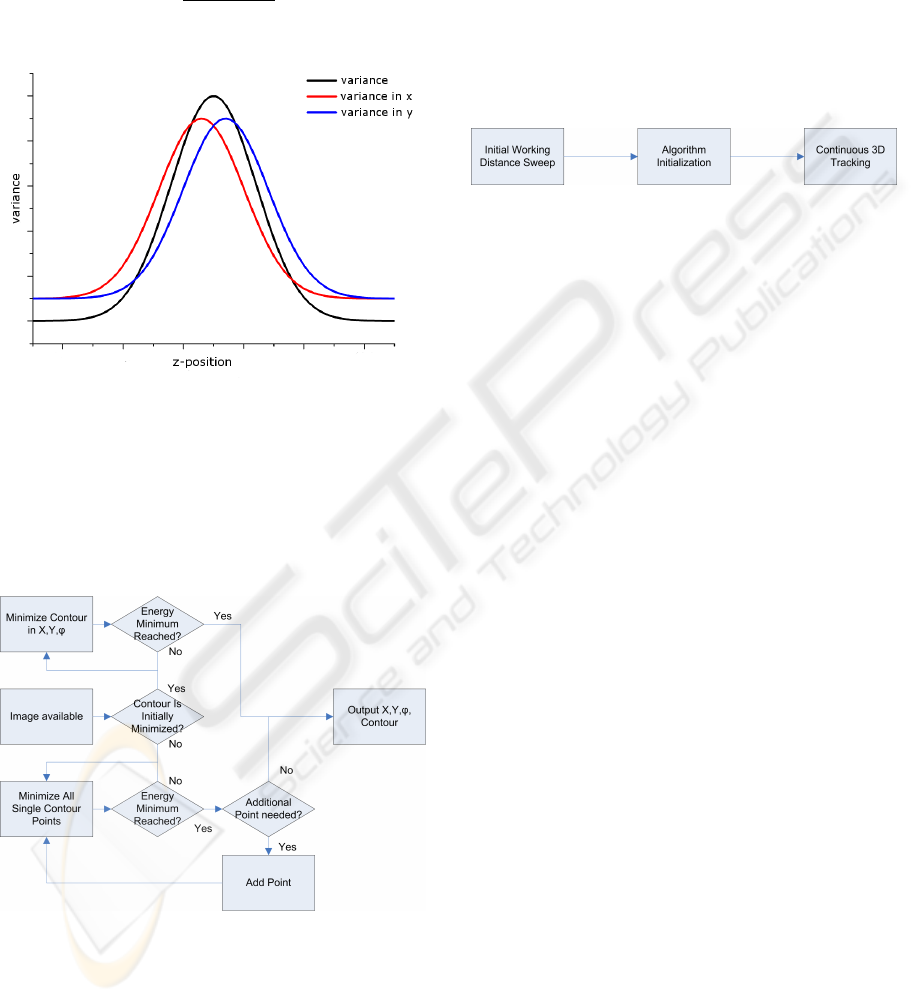
in ﬁgure 4, under the assumption that the object in the

image has suitable structure.

With the two curves having slightly displaced

maxima, we can estimate from the ratio of the two

values

r =

(I, A(C))

(11)

to which side the out-of-focus displacement occurs.

Figure 4: Expected curves for the different sharpness mea-

sures.

4 THE ALGORITHM

The twodimensional base algorithm is similar to the

active contour algorithm described in section 2. The

principle is depicted in ﬁgure 5. Important is that af-

Figure 5: The basic tracking algorithm for the twodimen-

sional part.

ter an initial free minimization, the tracker does only

translate and rotate the contour as a whole. This

is necessary to enable the out-of-focus estimator to

work, because else the enclosed area may change.

The same is valid for scaling, which is therefore dis-

abled in the algorithm. In order to enable continuous

threedimensional tracking, the algorithm has to be ini-

tialized like shown in ﬁgure 6. An initial working dis-

tance sweep is carried out to acquire the characteris-

tic curve of the tracked object. During this sweep, the

twodimensional tracking has to be enabled already.

After this, certain calculations and optimizations are

carried out on the acquired curves, e.g. it is made sure

that the curves are monotonic in sections. After the

data has been processed, the tracker can track contin-

uously until either object changes or imaging changes

require a reinitialization.

Figure 6: The initialization steps for the threedimensional

tracking.

The threedimensional tracking itself consists of

the twodimensional tracking algorithm, augmented

with a sharpness calculation component, an out-of-

focus displacement estimator and a direction estima-

tor, like shown in ﬁgure 7. The active contour tracker

delivers the twodimensional position and the segmen-

tation of the object. This segmentation is then used

to mask the original image. From the masked image,

the object sharpness is calculated using variance cal-

culation and the directional sharpness measures men-

tioned in the last section.

The variance value is used to estimate the out-of-

focus displacement by comparison with the data ac-

quired during initialization.

The directional sharpness values are used to es-

timate on which sidelobe of the initially acquired

sharpness curve the object is in the actual image. Af-

ter this is known, the information about the displace-

ment value and the displacement direction is com-

bined with the working distance at which the current

image was captured. The result is the estimated work-

ing distance at which the object is placed. This is then

joined with the position information from the twodi-

mensional tracking to generate a complete coordinate

set.

5 EXPERIMENTS

For the evaluation of the algorithm, the performance

has been tested in a setup inside the SEM. Target ob-

ject was a chessboard pattern as seen in ﬁgure 8. This

chessboard pattern has been put on a stub which is

mounted to a XYZ positioning setup using piezo slip-

stick actuated axes with internal position sensors. For

the experiment, the internal sensors of the axes were

read out and the acquired data joined with the track-

THREEDIMENSIONAL TRACKING USING OBJECT DEFOCUS - In Twodimensional Scanning Electron Microscope

Images

Figure 7: The complete 3D tracking algorithm in the initial-

ized state.

ing data. During the experiment the axes were moved

in closed loop mode using the internal sensors. The

movement was in a pattern to verify the algorithm per-

formance. All measurements have been executed at a

magniﬁcation of 800x and a scanspeed of 5 (frame av-

eraging of 2

frames) on a LEO scanning electron mi-

croscope. The twodimensional pattern of the move-

ment has a size of 21µm times 39µm. The pattern

has been repeated at the z-axis positions of 0.17mm,

0.256mm and 0.32mm.

6 RESULTS

The ﬁrst result was the generation of the expected

curves from ﬁgure 4. The result can be seen in ﬁg-

ure 9. The shift of the variance calculated in rows and

columns separately is clearly visible, which enables

the algorithm to work in the anticipated way, estimat-

ing the direction of the defocusing.

As can be seen in ﬁgure 10, the movement pat-

tern used incorporated movement along each axis as

well as in diagonal. Also visible is the distortion of

the shape in comparison to the acquired sensor val-

ues. The reason for this was determined in additional

tests to be a decalibrated sensor of one of the axes.

This sensor did not deliver the correct position value,

resulting in the closed loop control positioning to a

wrong real axis position.

In ﬁgure 11 and ﬁgure 12 this gets more obvious.

While the tracking position in ﬁgure 12 closely fol-

lows the sensor information, this is not the case in ﬁg-

ure 11. Apart from the decalibrated sensor it can be

Figure 8: The structure used for the experiment, a chess-

board pattern mounted on a XYZ positioning setup. Visible

is the active contour tracking and segmenting one chess-

board block.

0 , 0 0 0 1 0 0 , 0 0 0 1 5 0 , 0 0 0 2 0 0 , 0 0 0 2 5 0 , 0 0 0 3 0 0 , 0 0 0 3 5 0 , 0 0 0 4 0 0 , 0 0 0 4 5

2 5 0 0

3 0 0 0

3 5 0 0

4 0 0 0

4 5 0 0

5 0 0 0

V a r i a n c e

z P o s

V a r i a n c e

V a r i a n c e X

V a r i a n c e Y

Figure 9: Measured curves for the variance and the variance

calculated in rows and columns separately.

stated that the twodimensional tracking is working.

In order to verify the tracking, the experiment was

repeated with a working and calibrated y-axis. The

twodimensional tracking can be seen in ﬁgure 13. The

shape of the movement is correct and the tracking is

working and stable.

Figure 14 shows the determined z-Position from

the tracking algorithm. Visible is that there is a certain

systematic error in the tracked position, as the calcu-

lated values deviate from the expected values. The

set working distance of the SEM is in the middle of

the working distance range shown in ﬁgure 14, at the

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

9 , 7 2 9 , 7 4

1 0 , 2 0

1 0 , 2 2

Y - p o s i t i o n [ m m ]

X - p o s i t i o n [ m m ]

s e t p o s i t i o n

t r a c k e d p o s i t i o n

Figure 10: Tracked X-Y position of the chessboard pattern.

The distorted shape and deviations are due to a decalibrated

actuated axis for the y-direction.

1 0 , 1 8 5

1 0 , 1 9 0

1 0 , 1 9 5

1 0 , 2 0 0

1 0 , 2 0 5

1 0 , 2 1 0

1 0 , 2 1 5

1 0 , 2 2 0

y - p o s i t i o n [ m m ]

t i m e

a x i s p o s i t i o n

t r a c k e d p o s i t i o n

Figure 11: The tracked and set y-position over time.

9 , 7 0

9 , 7 1

9 , 7 2

9 , 7 3

9 , 7 4

9 , 7 5

9 , 7 6

x - p o s i t i o n [ m m ]

t i m e

a x i s p o s i t i o n

t r a c k e d p o s i t i o n

Figure 12: The tracked and set x-position over time.

value 0.28. The problem which occurs here is that the

algorithm is most accurate not in the point of maxi-

mal focus, but within a certain range on the sidelobes

of the sharpness curve. As can be seen in ﬁgure 9,

the sharpness curve is relatively ﬂat around the max-

imum. In this interval around the maximum, small

changes in detected sharpness, which may also oc-

cur due to time variant behavior of the SEM imaging

process or due to certain changes in the surrounding

setup, will result in large errors in the estimated out-

of-focus displacement. This explains also not only

the big deviation from the axis set value, but also the

large amount of variation during the movement on the

y - p o s i t i o n

x - p o s i t i o n

Figure 13: Tracked X-Y position of the chessboard pattern

in the repeated measurement.

0 , 1 5

0 , 2 0

0 , 2 5

0 , 3 0

0 , 3 5

0 , 4 0

z - p o s i t i o n [ m m ]

T i m e

Figure 14: The tracked z-position over time.

same z-position. So it has to be stated that the opti-

mal working condition for this algorithm is a slightly

defocused image.

In ﬁgure 15 the tracking result can be seen in three

dimensions. The movement pattern is qualitatively

visible, though the tracking in z-direction is not as

good as in the image plane. Still the goal of the algo-

rithm design has been reached, an estimate has been

calculated for the z-position of the object which is

principally useable.

Z A x i s

Y A x i s

X A x i s

Figure 15: The tracked movement in 3D.

THREEDIMENSIONAL TRACKING USING OBJECT DEFOCUS - In Twodimensional Scanning Electron Microscope

Images

7 SUMMARY

In this paper a threedimensional tracking algorithm

for the tracking of objects in the SEM has been pre-

sented. The algorithm takes advantage of the image

defocusing which is evident when objects leave the

focal plane. A twodimensional tracking algorithm

based on active contours with a region-based mini-

mization has been taken as the base algorithm. Added

extensions include the segmentation of the object and

the consecutive sharpness calculation. Additionally

the variance of the rows and columns is calculated

separately for determining the direction of the defo-

cusing. This enables the analysis of the sharpness in

different directions. If the image contains astigma-

tism, it is possible to estimate if the image focal plane

lies in front of or behind the object. Experiments

have shown that this approach is working and after

an initialization phase qualitatively delivers a three-

dimensional position information. The z-position still

contains a systematic error, which is most inﬂuential

around the best focused point. This error has to be

diminished by further analysis and change and op-

timization of the implementation. Overall the feasi-

bility of this threedimensional tracking algorithm has

been shown.

REFERENCES

Blake, A. and Isard, M. (2000). Active Contours. Springer.

Dahmen, C. (2008). Focus-based depth estimation in the

sem. In Proceedings of the International Sympo-

sium on Optomechatronic Technologies 2008, volume

7266, page 72661O. SPIE.

Eichhorn, V., Fatikow, S., Wich, T., Dahmen, C., Sievers,

T., Andersen, K., Carlson, K., and Bøggild, P. (2008).

Depth-detection methods for microgripper based cnt

manipulation in a scanning electron microscope. Jour-

nal of Micro-Nano Mechatronics. accepted.

Fatikow, S. (2007). Automated Nanohandling by Micro-

robots.

Fernandez, J., Sorzano, C., Marabini, R., and Carazo, J.

(2006). Image processing and 3-D reconstruction in

electron microscopy. Signal Processing Magazine,

IEEE, 23(3):84–94.

ahnisch, M. and Fatikow, S. (2007). 3d vision feedback for

nanohandling monitoring in a scanning electron mi-

croscope. International Journal of Optomechatronics,

1(1):4–26.

Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:

Active contour models. International Journal of Com-

puter Vision, 1(4):321–331.

Kratochvil, B. E., Dong, L. X., and Nelson, B. J. (2007).

Real-time rigid-body visual tracking in a scanning

electron microscope. In Proc. of the 7th IEEE Conf.

on Nanotechnology (IEEE-NANO2007), Hong Kong,

China.

Sievers, T. (2006). Global sensor feedback for automatic

nanohandling inside a scanning electron microscope.

In Proc. of 2nd I*PROMS NoE Virtual International

Conference on Intelligent Production Machines and

Systems, pages 289–294.

Sievers, T. (2007). Echtzeit-Objektverfolgung im

Rasterelektronenmikroskop. PhD thesis, Univer-

sity of Oldenburg.

Sievers, T. and Fatikow, S. (2006). Real-time object track-

ing for the robot-based nanohandling in a scanning

electron microscope. Journal of Micromechatronics,

3(3-4):267–284.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics