INDUCING COOPERATION IN FUZZY CLASSIFICATION

RULES USING ITERATIVE RULE LEARNING AND

RULE-WEIGHTING

Omid Dehzangi, Ehsan Younessian

Nanyang Technological Universit, Singapore

Fariborz Hosseini Fard

SoundBuzz PTE LTD, Subsidiary of Motorola Inc., Singapore

Keywords: Fuzzy Systems, Classification, Iterative Rule Learning (IRL), Rule Weighting, ROC.

Abstract: Fuzzy Rule-Based Classification Systems (FRBCSs) focus on generating a compact rule-base from

numerical input data for classification purposes. Iterative Rule Learning (IRL) has been proposed to reduce

the search space for learning a rule-set for a specific classification problem. In this approach, a rule-set is

constructed by searching for an appropriate fuzzy rule and adding it to the rule-set in each iteration. A major

element of this approach is the requirement of an evaluation metric to find the best rule in each iteration.

The difficulty in choosing the best rule is that the evaluation metric should be able to measure the degree of

cooperation of the candidate rule with the rules found so far. This poses a major difficulty when dealing

with fuzzy rules; because unlike crisp rules, each pattern is compatible with a fuzzy rule only to a certain

degree. In this paper, the cooperation degree of a candidate rule is divided into the following two

components: I)- The cooperation degree of the rule with other rules of the same class, II)- The cooperation

degree of the rule with rules of the other classes. An IRL scheme to generate fuzzy classification rules is

proposed that induces cooperation among the rules of the same class. Cooperation between the rules of

different classes is handled using our proposed rule-weighting mechanism. Through a set of experiments on

some benchmark data sets from UCI-ML repository, the effectiveness of the proposed scheme is shown.

1 INTRODUCTION

The main application area of fuzzy rule-based

systems has been control problems (Sugeno, 1985).

Fuzzy rule-based systems for control problems can

be viewed as approximators of nonlinear mappings

from non-fuzzy input vectors to non-fuzzy output

values. Recently, fuzzy rule-based systems have

often been applied to classification problems where

non-fuzzy input vectors are to be assigned to one of

a given set of classes. Many approaches have been

proposed for generating and learning fuzzy if-then

rules from numerical data for classification

problems. For instance, FRBCSs are created by

simple heuristic procedures (Ishibuchi et al., 1992),

(Abe, 1995), neuro-fuzzy techniques (Nauck and R.

Kruse, 1997), clustering methods (Abe and

Thawonmas, 1997), genetic algorithms (Ishibuchi et

al., 2005), etc.

Pattern classification has been the main issue in

machine learning. Classification is to acquire

knowledge from a set of training patterns and use

this knowledge to predict the class of a new pattern.

FRBCSs use fuzzy rules as a mean to perform

classification tasks. A rule is an if-then relation from

the n-dimensional pattern space to the set of classes.

In a single winner rule approach (Ishibuchi and

Nakashima, 2001), to classify an unknown pattern,

one rule is selected and used to classify the pattern.

In this paper, a single winner rule approach is used

which will be discussed later. In the broadest sense,

any method that incorporates information from

training samples in the design of a classifier employs

learning. Therefore, designing classifiers involves

some type of learning to learn or estimate unknown

parameters using a set of labeled patterns.

Dehzangi O., Younessian E. and Hosseini Fard F. (2009).

INDUCING COOPERATION IN FUZZY CLASSIFICATION RULES USING ITERATIVE RULE LEARNING AND RULE-WEIGHTING.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,

pages 62-67

DOI: 10.5220/0002209900620067

 SciTePress

In this paper, an IRL approach for fuzzy rule

selection is presented in which the degree of

cooperation of each candidate rule with other rules

of the same class is estimated. In this approach, the

final rule-set for classification is constructed by

searching for an appropriate fuzzy rule and adding it

to the rule-set in each step. Then, a simple rule-

weighting mechanism is proposed to reach some

degrees of cooperation/competition among the rules

of different classes. Four UCI ML driven data sets

are then used to evaluate the proposed fuzzy

classification method.

2 FUZZY CLASSIFICATION

RULES

In the design of fuzzy rule-based systems, we face

two conflicting objectives: error minimization and

interpretability maximization. Error minimization

has been used in many applications of fuzzy rule-

based systems in the literature while the

interpretability was not usually taken into account in

those applications. Recently, the tradeoff between

these two objectives has been discussed in some

studies. When fuzzy rule-based systems are used for

two-dimensional problems, fuzzy rules can be

represented in a tabular form (Ishibuchi and

Yamamoto, 2004). Figure 1 shows an example of a

fuzzy rule table for a two-dimensional pattern

classification problem. In this figure, we have the

following four fuzzy rules:

is small and

is small then Class 1,

is small and

is large then Class 2,

is large and

is small then Class 3,

is large and

is large then Class 4,

where small and large are linguistic values defined

by triangular membership functions.

Figure 1: Four fuzzy rules in the 2-dimensional pattern

space

[0,1] [0,1]×

As shown in Figure 1, fuzzy rules for 2-dimensional

problems can be written in a human understandable

manner using the tabular form representation. When

fuzzy rule-based systems are applied to high-

dimensional problems, their interpretability is

significantly degraded due to the two difficulties: the

increase in the number of fuzzy rules and the

increase in the number of antecedent conditions of

each fuzzy rule.

Assume that we have m labeled patterns

=(x

,…, x

)

, p=1,2,…,m from M classes in an n-

dimensional continuous pattern space is given. For

classification problems with n number of attributes

as in (Ishibuchi and Yamamoto, 2004), we use fuzzy

rules of the following form:

Rule

R : If

and … and

then class

C with

(1)

where R

is the i-th rule, X=(x

,…,x

) is an n-

dimensional pattern vector, A

is an antecedent fuzzy

set (i.e., linguistic value such as small or large in

Figure 1), C

is the class label of R

, and CF

is the

weight of R

. It should be noted that the consequent

part of our fuzzy rule for classification problems is

totally different from standard fuzzy rules for

function approximation problems. The consequent

of our fuzzy rule is a non-fuzzy class label and the

rule weight CF

is a real number in the unit interval

[0, 1]. The rule weight is used as the strength of each

fuzzy rule when a new pattern is classified by a

fuzzy rule-based classification system (see

(Ishibuchi and Nakashima, 2001) for details).

The compatibility grade of a training pattern X

with the antecedent part A

=(A

,…,A

i,n

) of fuzzy rule

is calculated using product operator as,

() ( ) ( )

ii in

Ap A p A pn

XX X

μμ

×⋅⋅⋅×

(2)

where

()

⋅

is the membership function of the

antecedent fuzzy set

3 CANDIDATE RULE

GENERATION

In our approach, fuzzy if-then rules are generated

from numerical data. Then, the generated rules are

used as candidate rules from which a small number

of fuzzy if-then rules are selected in an iterative

manner. The domain interval of each attribute x

discretized into K

fuzzy sets. Figure 2 shows some

examples of fuzzy discretization.

INDUCING COOPERATION IN FUZZY CLASSIFICATION RULES USING ITERATIVE RULE LEARNING AND

RULE-WEIGHTING

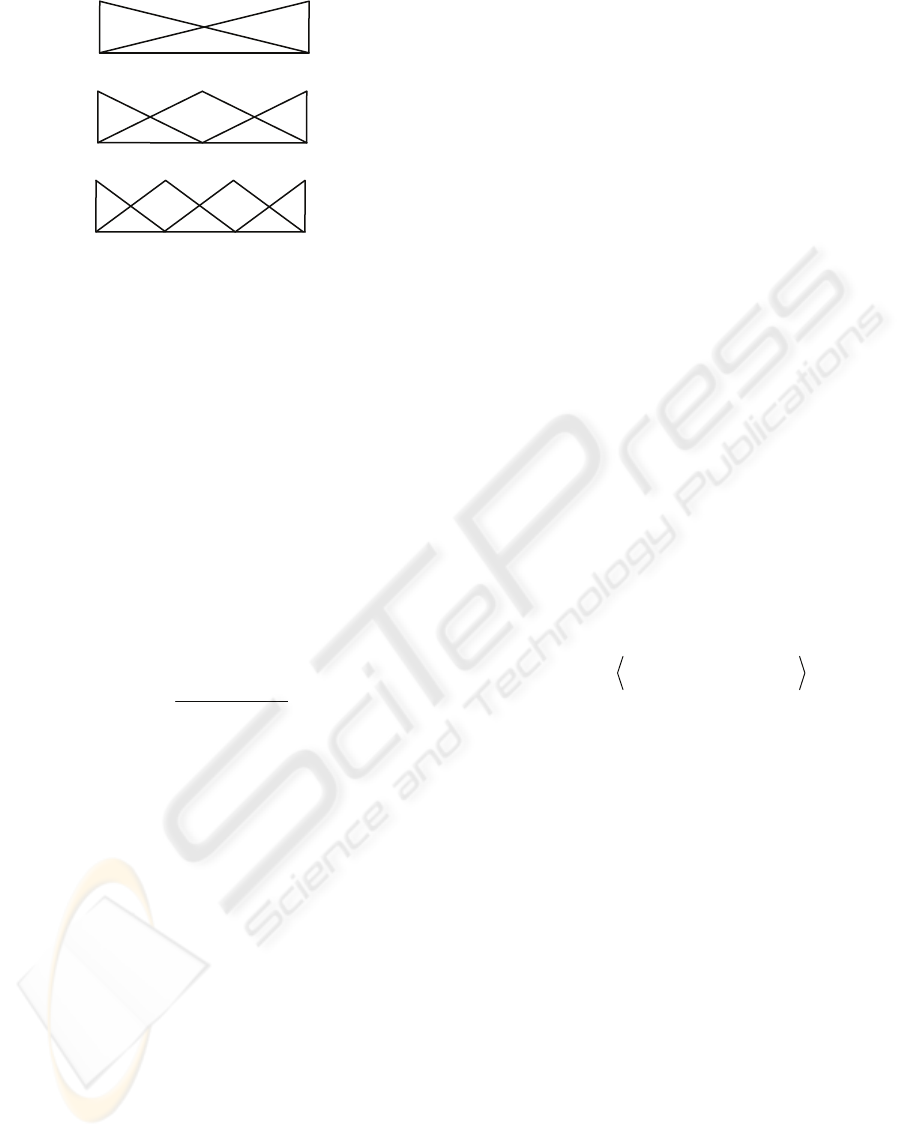
Figure 2: Some typical examples of fuzzy partitions of the

domain interval [0, 1].

The meaning of each label is as follows:

S: small, MS: medium small, M: medium, ML:

medium large, and L: large. The superscript of each

label denotes the granularity of the corresponding

fuzzy partition.

Each antecedent fuzzy set in a fuzzy rule can be

one of K

fuzzy sets or “don't care”. Therefore the

total number of possible antecedent combinations is

+1)×…× (K

+1).

To determine the consequent part of a rule, we

use a concept in data mining called confidence

degree. The confidence of a fuzzy association rule is

defined as (Ishibuchi and Yamamoto, 2004):

()

(

)

()

xclassh

cA classh

∈

⇒=

∑

(3)

The consequent class C

of the fuzzy rule R

specified by identifying the class with the maximum

confidence. If the maximum confidence of a rule is

zero or the difference between the first and second

maximum confidences is zero, the rule is not

generated.

To avoid coping with a large number of

candidate rules in the rule selection procedure, some

prescreening criterion is needed. Several criteria is

used in the previous works (Gonzalez and Perez,

1999). In this paper we use the following criterion:

(class ) () ()

iApAp

xclassh xclassh

value A h X X

μμ

∈∉

⇒= −

∑∑

(

4 RULE SELECTION

After generating the candidate rules, a set of rules

must be selected to construct the rule-base of the

classifier. The rules are selected in an iterative

manner. The generated fuzzy if-then rules are

divided into M groups according to their consequent

classes. Fuzzy if-then rules in each group are sorted

in descending order of the evaluation criterion (4).

In the first step of the rule selection the best rule

of each class is added to the rule-base. To build a

rule-base with N rules (

NM≥

), the remaining N-

M rules are selected one by one. A major element of

this approach is the need of an evaluation metric to

find the best rule in each iteration.

The difficulty in choosing the best rule is that the

evaluation metric should be able to measure the

degree of cooperation of the candidate rule with the

rules found so far. This is a major difficulty when

dealing with fuzzy rules, due to the fact that each

pattern is compatible with a fuzzy rule to a certain

degree.

For the rules found so far, a measure called

“fuzzy accuracy measure” of the rule-base is defined

as:

(

)

(

)

()

class class

max max

rule base R p R p

xh xh

R rule base R rule base

μμ

−

∈∉

∈− ∈−

=−

∑∑

(5)

The aim of this measure is to calculate the

overall effectiveness of the rules of the same class

that are found so far. To add the rule R

from the set

of candidate rules to the rule-base, the rule that

improves F

rule-base

the most is chosen:

{}

arg max

w rule base R rule base

R Candidate Rules

RFF

−−

∈

=−

∪

(6)

The process of rule selection is continued

iteratively as long as there are further improvements

in F

rule-base

. The proposed scheme both induces

cooperation among the rules of the same class and

avoids including redundant rules in the final rule-

base which results in having a compact rule-base.

5 INDUCTING COOPERATION

WITH RULE WEIGHTING

The first component of the cooperation of the newly

added rule is its degree of cooperation with the rules

of the same class. This component is considered in

the rule selection phase. The second component of

the cooperation is the degree of cooperation between

rules of different classes. This component is also

called competition. Competition among the rules of

different classes

is handled by assigning a weight to

each different rule.

In (Nauck & Kruse, 1998), the effect of rule

weights in fuzzy rule-based systems for function

0.0 1.0

1.0

0.0

1.0

0.0

1.0

0.0

0.0 1.0

MS ML

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

approximation problems is discussed. They also

showed how the modification of the membership

functions of antecedent or consequent fuzzy sets can

be equivalently replaced by the learning of rule

weights. Several heuristic criteria for rule-weighting

have been introduced in earlier works done by

Ishibuchi et al (Ishibuchi and Yamamoto, 2004)

which are briefed here:

()

CAcCF ⇒=

(7)

() ()

ii ii

CF c A C c A C

≠

=⇒− ⇒

∑

(8)

(

)

()

{}

max 1, 2,... ;

CF c A C

cA Classtt Mt C

=⇒

−⇒=≠

(9)

()

(

)

()

∑

∉

−⇒=

CClassx

CAcCF

(10)

where c(

C⇒

) is the confidence of a fuzzy rule

, and

()

is the compatibility grade of a

training pattern X

with the antecedent part of fuzzy

rule R

In the following, a simple rule-weighting

criterion is presented. In our suggested method, it is

tried to reach some degrees of cooperation

/competition among the rules of different classes. To

calculate the weight of the fuzzy rule R

, first a value

is calculated named as contrast for each training

data point X

(

)

(

)

() ()

()

1,...,

()

1,...,

()

max

() ,

max

label R C

Rp R p

label R C

Contrast X

μμ

≠

(11)

where R

is the rule that is being weighted. If a data

point is covered by the rules of other classes, the

contrast value of this data point, with respect to the

rule in hand, is close to one; otherwise it is closer to

zero.

Data points are sorted in ascending order of their

contrast values. The next step is to find a threshold

of the contrast values, ω, that best separates the data

points of the same class from the data points of other

classes. In this way, each data point X

for which

()

Contrast X < ω is assumed to be of the same

class as R

. The threshold is then altered from the list

contrast value to the greatest and accuracy of the

classifier with respect to the current threshold is

measured. The weight of rule R

is obtained from the

the value of the best threshold (i.e. leading to the

highest accuracy) normalized in the range of [0, 1]

as follows,

(12)

6 EXPERIMENTAL RESULTS

In our experiments, we used four data sets in Table 1

available from the UCI ML repository (Merz and

Murphy, 1996).

Table 1: Statistics of the data sets used in our experiments.

Data set

# of

attributes

# of

patterns

# of

Classes

Pima 8 768 2

Wine 13 178 3

Cancer Wis. 9 699 2

Glass 9 214 6

All attribute values of the four data sets were

normalized into real numbers in the unit interval

[0, 1] before extracting fuzzy rules. Since we did not

know an appropriate fuzzy partition for each

attribute of each test problem, we simultaneously

used three different fuzzy partitions in Figure 2. One

of the 9 triangular fuzzy sets was used as an

antecedent fuzzy set. To generate simple fuzzy rules

(i.e., short fuzzy rules with a small number of

antecedent conditions), we also used “don’t care” as

an antecedent fuzzy set. The membership function of

“don’t care” is defined as μ

“dontcare”

(X) = 1. The total

number of combinations of antecedent fuzzy sets is

for an n-dimensional problem.

In our computational experiments we only

examined fuzzy rules with three or less antecedent

conditions (i.e., with n-3 or more “don’t care”

conditions). The restriction on the number of

antecedent conditions is to generated interpretable

fuzzy rules as well as for decreasing the CPU time.

In Tables 2-5, the results of the fuzzy

classification system using the proposed fuzzy rule

selection method with different rule-weighting

methods are shown on the data sets of Table 1. All

the reported results are the average of ten trials of

ten-fold cross validation. The first column of each

Table is the number of rules used to classify the data

points in the selected data set. The other five

columns represent the classification accuracy of the

INDUCING COOPERATION IN FUZZY CLASSIFICATION RULES USING ITERATIVE RULE LEARNING AND

RULE-WEIGHTING

four mentioned weighting methods proposed in

(Ishibuchi and Yamamoto, 2004) compared to our

proposed method. As it can be seen in the results,

the proposed method led to the best results among

the rule-weighting methods. In each row of the

Table 2-5, the method which had the best result is

bolded.

Table 2: Test data classification rates of Glass dataset.

Table 3: Test data classification rates of Wine dataset.

# of

rules

Weight

CF1 CF2 CF3 CF4

Our

Meth

3 84.90 87.27 87.82 86.99 85.97 85.54

6 91.55 92.53 93.31 91.69 91.85 93.14

9 93.14 91.89 92.28 92.86 94.14 91.97

12 92.88 94.81 94.96 93.77 93.38 92.11

15 93.94 93.16 94.84 94.69 93.44 95.51

18 94.57 93.86 93.78 93.60 92.73 95.48

51 95.33 95.00 94.56 94.64 93.34 95.60

56 95.18 94.37 94.66 94.53 94.42 95.64

Table 4: data classification rates of Cancer dataset.

# of

rules

Weight

CF1 CF2 CF3 CF4

Our

Method

2 81.84 83.29 80.81 81.06 83.16 83.13

3 91.79 91.25 91.65 92.67 92.04 91.16

4 89.61 91.41 92.34 92.44 92.36 91.61

5 92.87 91.34 90.35 90.57 93.08 92.20

6 93.16 93.66 93.32 92.55 92.59 90.81

9 90.44 94.55 91.98 91.00 91.14 94.82

12 92.66 92.87 90.70 91.63 92.60 94.91

17 93.49 91.66 92.34 92.25 91.73 95.44

Table 5: Test data classification rates of Pima dataset.

# of

rules

Weight

CF1 CF2 CF3 CF4

Our

Method

2 68.53 69.80 69.34 68.10 69.20 68.85

5 69.1 71.66 68.64 70.22 68.22 73.64

7 68.15 70.28 71.05 69.20 70.34 76.03

10 70.52 69.59 68.47 70.52 70.38 74.23

18 71.79 70.08 70.59 70.36 70.49 74.92

27 73.11 70.1 70.73 70.46 70.99 75.24

37 71.40 70.53 72.32 71.67 70.39 75.78

50 70.97 72.56 71.32 71.86 71.47 76.22

Although the classification accuracy has always

been the main concern in classification problems,

interpretability also have to be considered.

There are two factors that heavily affect the

interpretability of a rule-based system: number of

the generated rules and number of antecedent

conditions of each generated rule. As shown, our

proposed method is highly interpretable in terms of

both number the generated fuzzy classification rules

and their number of antecedent conditions.

In Table 6, we compared our results to the

results obtained by another successful rule-based

method as benchmark results called C4.5 reported

by (Elomaa and Rousu, 1999). As shown in Table 6,

except in one case, the proposed classifier in this

paper shows higher classification rates.

Table 6: Accuracy of the proposed classifier compared to

C4.5. The best result in each row is highlighted by

boldface.

Data set

The proposed

classifier (%)

C4.5 classifier

Worst (%) Best (%)

Pima

76.2

72.8 75.0

Cancer

95.4

94.0 94.9

Wine

95.6

92.2 94.4

Glass 68.6 68.8 72.7

7 CONCLUSIONS

In this paper, the cooperation degree of the fuzzy

classification rules was divided into the two

components: I)- The cooperation degree of the rules

with other rules of the same class, II)- The

cooperation degree of the rules with rules of the

other classes. We proposed an IRL method for fuzzy

rule selection. Using the proposed criterion, it was

possible to estimate the degree of cooperation of a

candidate rule with other rules of the same class in

# of

rules

Weight

CF1 CF2 CF3 CF4

Our

Method

6 49.61 48.95 49.42 48.71 54.15 56.99

12 55.72 58.03 58.80 60.56 60.37 63.89

18 57.81 59.43 58.37 59.41 63.08 66.29

24 61.25 60.85 63.18 60.47 62.38 67.18

30 61.35 63.05 61.47 61.33 63.78 67.47

36 62.08 62.37 63.68 62.13 65.51 68.11

42 61.21 60.28 61.75 63.53 64.18 68.29

45 62.98 61.63 63.14 64.22 65.01 68.62

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

the final rule-base. Furthermore, a simple rule-

weighting mechanism was proposed to reach some

degrees of cooperation/competition among the rules

of different classes. The experimental results on real

problems like speech data classification showed the

effectiveness of the proposed method to generate

fuzzy classification rules with high degrees of

cooperation among them.

REFERENCES

Ishibuchi H., Nakashima T., 2001. Effect of Rule Weights

in Fuzzy Rule-Based Classification Systems. IEEE

Transaction on Fuzzy Systems.

Sugeno M., 1985. An introductory survey of fuzzy control,

Information Sciences, 36: 59-83.

Ishibuchi H., Nozaki K., Tanaka H., 1992. Distributed

representation of fuzzy rules and its application

topattern classification. Fuzzy Sets Systems, 52: 21-32.

Abe S., Lan M., 1995. A method for fuzzy rules extraction

directly from numerical data and its applicationto

pattern classification. IEEE Trans. on Fuzzy Systems,

3: 18-28.

Nauck D., Kruse R., 1997. A neuro-fuzzy method to learn

fuzzy classification rules from data. Fuzzy Sets and

Systems, 89: 277-288.

Abe S., Thawonmas R., 1997. A fuzzy classifier with

ellipsoidal regions. IEEE Trans. on Fuzzy Systems, 5:

358-368.

Ishibuchi, H., Yamamoto, T., Nakashima, T., 2005.

Hybridization of Fuzzy GBML Approaches for Pattern

Classification Problems, IEEE Transaction on

Systems, Man, and Cybernatics.

Gonzalez, A., Perez, R., 1999. SLAVE: A genetic learning

system based on an iterative approach, IEEE Trans. on

Fuzzy Systems, 7: 176-191.

Ishibuchi H., Yamamoto T., 2004. Comparison of

Heuristic Criteria for Fuzzy Rule Selection in

Classification Problems. Kluwer Academic

Publishers.

Nauck, D., Kruse, R., 1998. How the learning of rule

weights affects the interpretability of fuzzy systems,”

Proc. of 7th IEEE International Conference on Fuzzy

Systems, 1235-1240.

Ishibuchi H., Yamamoto T., 2003. Effects of Three-

Objective Genetic Rule Selection on the

Generalization Ability of Fuzzy Rule-based Systems,

The Genetic and Evolutionary Computation

Conference.

Merz, C.J., Murphy, P.M., 1996. UCIRepository of

Machine Learning Databases. Irvine, CA: University

of California Irvine, Department of information and

Computer Science. Internet:

http://www.ics.uci.edu/~mlearn/MLRepository.html

Elomaa, T., Rousu, J., 1999. General and efficient

multisplitting of numerical attributes, Machine

Learning 36: 201-244.

INDUCING COOPERATION IN FUZZY CLASSIFICATION RULES USING ITERATIVE RULE LEARNING AND

RULE-WEIGHTING