BATCH REINFORCEMENT LEARNING
An Application to a Controllable Semi-active Suspension System
Simone Tognetti, Marcello Restelli, Sergio M. Savaresi
Dipartimento di elettronica e informazione, Politecnico di Milano, via Ponzio 34/5, 20133 Milano, Italy
Cristiano Spelta
Dipartimento di Ingegneria dellInformazione e Metodi Matematici, Universit degli Studi di Bergamo
viale Marconi 5, 24044 Dalmine (BG), Italy
Keywords:
Batch-reinforcement learning, Control theory, Non linear optimal control, Semi-active suspension.
Abstract:
The design problem of optimal comfort-oriented semi-active suspension has been addressed with different
standard techniques which failed to come out with an optimal strategy because the system is hard non-linear
and the solution is too complex to be found analytically. In this work, we aimed at solving such complex
problem by applying Batch Reinforcement Learning (BRL), that is an artificial intelligence technique that
approximates the solution of optimal control problems without knowing the system dynamics. Recently,
a quasi optimal strategy for semi-active suspension has been designed and proposed: the Mixed SH-ADD
algorithm, which the strategy designed in this paper is compared to. We show that an accurately tuned BRL
provides a policy able to guarantee the overall best performance.
1 INTRODUCTION
Among the many different types of controlled suspen-
sion systems (see e.g., (Sammier et al., 2003; Savaresi
et al., 2005; Silani et al., 2002)), semi-active sus-
pensions have received a lot of attention since they
provide the best compromise between cost (energy-
consumption and actuators/sensors hardware) and
performance. The research activity on controllable
suspensions develops along two mainstreams: the de-
velopment of reliable, high-performance, and cost-
effective semi-active controllable shock-absorbers
(Electro-Hydraulic or Magneto-Rheological see e.g.,
(Ahmadian et al., 2001; Guardabassi and Savaresi,
2001; Valasek et al., 1998; Williams, 1997)), and
the development of control strategies and algorithms
which can fully exploit the potential advantages of
controllable shock-absorbers. This work focuses on
the control-design issue for road vehicles.
The design problem of optimal comfort oriented
semi-active suspension has been addressed with dif-
ferent standard techniques which failed to came out
with an optimal strategy because the system is hard
non-linear and the solution is too complex to be found
analytically. The literature offers many contributions
that provide approximate solutions to the non-linear
problem, or alternatively, the non-linearity is par-
tially removed to exploit linear techniques (see e.g.,
(Karnopp and Crosby, 1974; Sammier et al., 2003)-
(Savaresi and Spelta, 2008; Valasek et al., 1998)).
In this work, we aimed at solving the optimal con-
trol problem of comfort-oriented semi-active suspen-
sion by using Batch Reinforcement Learning (BRL).
Developed in the artificial intelligent research field,
BRL provides numerical algorithms able to approxi-
mate the solution of an optimal-control problem with-
out knowing the system dynamics (see (Kaelbling
et al., 1996) and (Sutton and Barto, 1998)). The al-
gorithm is independent from the model complexity
and can be trained on the real system without knowing
its dynamics. We compared the strategy obtained by
BRL with the ones given by the state-of-the-art semi-
active control algorithms. We showed that an accu-
rately tuned BRL provides a policy able to guarantee
the overall best performance.
The outline of the paper is as follows. In Sec-
tion 2 the control problem is stated. Section 3 re-
calls the BRL technique. Section 4 sums up the de-
sign of BRL-based control rule. Section 5 motivates
the choice of algorithm parameters, section 6 presents
228
Tognetti S., Restelli M., M. Savaresi S. and Spelta C. (2009).
BATCH REINFORCEMENT LEARNING - An Application to a Controllable Semi-active Suspension System.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,
pages 228-233
DOI: 10.5220/0002210302280233
Copyright
c
 SciTePress

experimental results, and finally, section 7 ends the
paper with some concluding remarks.
2 PROBLEM STATEMENT AND
PREVIOUS WORK
The dynamic model of a quarter-car system equipped
with semi-active suspensions can be described by
the following set of differential equations (Williams,
1997):









M ¨z(t) = −c(t)(˙z(t) − ˙z
t
(t)) − k(z(t) − z
t
(t) − ∆
s
) − Mg
m¨z
t
(t) = c(t)(˙z(t) − ˙z
t
(t)) + k(z(t) − z
t
(t) − ∆
s
)+
−k
t
(z
t
(t) − z
r
(t) − ∆
t
) − mg [z
t
(t) − z
r
(t) < ∆
t
]
˙c(t) = −βc(t) + βc
in
(t) [ ˆc
min
≤ c
in
(t) ≤ ˆc
max
]
(1)
where the symbols in (1) are as follows (see also
Figure 1): z(t), z
t
(t),z
r
(t) are the vertical positions of
the body, the unsprung mass, and the road profile, re-
spectively. M is the quarter-car body mass; m is the
Figure 1: Quarter-car diagram.
unsprung mass (tire, wheel, brake caliper, suspension
links, etc.); k and k
t
are the stiffnesses of the suspen-
sion spring and of the tire, respectively; ∆
s
and ∆
t
are
the lengths of the unloaded suspension spring and tire,
respectively; c(t) and c
in
(t) are the actual and the re-
quested damping coefficients of the shock-absorber,
respectively.
The damping-coefficient variation is ruled by a
1st-order dynamic model, where β is the bandwidth;
consequently the actual damping coefficient remains
in the interval c
min
≤ c
in
(t) ≤ c
max
, where c
min
and
c
max
are design parameters of the semi-active shock-
absorber. This limitation is the so-called “passivity-
constraint” of a semi-active suspension.
For the above quarter-car model, the following set
of parameters are used (unless otherwise stated): M =
400 kg, m = 50 kg, k = 20 KN/m, k
t
= 250 KN/m,
c
min
= 300 Ns/m, c
max
= 3000 Ns/m and β = 100π.
Notice that (1) is non-linear since the damping co-
efficient c(t) is a state variable; in the case of a passive
suspension with a constant damping coefficient c, (1)
is reduced to a 4th-order linear system by simply set-
ting β → ∞ and c
in
(t) = c.
The general high-level structure of a comfort-
oriented control architecture for a semi-active suspen-
sion device is the following. The control variable is
the requested damping coefficient c
in
(t). The mea-
sured output signals are two: the vertical acceleration
¨z(t) and the suspension displacement z(t) − z
t
(t). The
disturbance is the road profile z
r
(t) (non-measurable
and unpredictable signal).
The goal of a comfort-oriented semi-active con-
trol system is to manage the damping of the shock-
absorber to filter the road disturbance towards the
body dynamics. Thus the following cost function is
introduced: J =
R
t
0
(¨z(t))
2
dt. It has been shown in
(Savaresi et al., 2005) that the optimal control strat-
egy is necessarily a rationale that switches from the
minimum to the maximum damping of the shock ab-
sorber (two-state algorithms).
In the literature there exist many control strategies
with a flavor of optimality: Skyhook (SH) (Karnopp
and Crosby, 1974) and Acceleration Driven Damping
(ADD) (Savaresi et al., 2005). Recently an almost
optimal control strategy has been developed: the so-
called Mixed SH-ADD (Savaresi and Spelta, 2007).
Similarly to SH, also this strategy requires a two-state
damper:







c
in
(t) = c
max
if

¨z
2
− α
2
˙z
2
6 0 ∧ ˙z(˙z − ˙z
t
) > 0

∨
∨

¨z
2
− α
2
˙z
2
> 0 ∧ ¨z(˙z − ˙z
t
) > 0

c
in
(t) = c
max
if

¨z
2
− α
2
˙z
2
6 0 ∧ ˙z(˙z − ˙z
t
) 6 0

∨
∨

¨z
2
− α
2
˙z
2
> 0 ∧ ¨z(˙z − ˙z
t
) 6 0

(2)
Notice that accordingly to the sign of ¨z
2
− α
2
˙z
2
an appropriate sub-strategy is selected. This quan-
tity is a frequency selector and α represents the de-
sired cross-over frequency between two suboptimal
strategies, namely SH and ADD (see. (Savaresi and
Spelta, 2007)). A single sensor implementation of this
strategy has been recently developed (the so-called 1-
Sensor-Mix, (Savaresi and Spelta, 2008)). SH, ADD
and Mixed SH-ADD have been already compared in
the time and frequency domains (Savaresi and Spelta,
2007).
3 REINFORCEMENT LEARNING
Research in Reinforcement Learning (RL) aims at
designing algorithms by which autonomous agents
BATCH REINFORCEMENT LEARNING - An Application to a Controllable Semi-active Suspension System
229

(controller) can learn to behave (estimation of control
policy) in some appropriate fashion in some environ-
ment (controlled system), from their interaction (con-
trol variable) with this environment or from observa-
tions gathered from the environment (see e.g. (Sutton
and Barto, 1998) for a broad overview).
The interaction between the agent and the environ-
ment is modeled as a discrete-time Markov Decision
Process (MDP). An MDP is a tuple < S , A,P , R ,γ >,
where S is the state space, A is the action space,
P : S ×A → Π(S) is the transition model that assigns
to each state-action pair a probability distribution over
S, R : S × A → Π(R) is the reward function, or cost
function, that assigns to each state-action pair a prob-
ability distribution over R, γ ∈ [0,1) is the discount
factor. At each time step, the agent chooses an action
according to its current policy π : S → Π(A), which
maps each state to a probability distribution over ac-
tions. The goal of an RL agent is to maximize the
expected sum of discounted rewards, that is to learn
an optimal policy π
∗
that leads to the maximization
of the action-value function, or cost-to-go from each
state.
The optimal action-value function Q
∗
(s(t),a(t))
s(t) ∈ S, a(t) ∈ A is defined by the Bellman equation:
Q
∗
(s(t),a(t)) =
∑
s(t+∆T )∈S
P (s(t + ∆T )|s(t), a(t))
h
R(s(t),a(t)) + γ max
a(t+∆T )∈A
Q
∗
(s(t + ∆T ),a(t + ∆T ))
i
(3)
where R(s,a) = E[R (s,a)] is the expected reward.
From the Control Theory perspective this equation
represents the optimal cost-to-go, indeed it represents
the discrete-time version of the Hamilton-Jacobi-
Bellman equation.
In order to manage the huge amount of samples
needed to solve real-world tasks, batch approaches
have been proposed (Riedmiller, 2005; Antos et al.,
2008; Ernst et al., 2005). The main idea is to distin-
guish between the exploration strategy that collects
samples (sampling phase), and the off-line learning
algorithm that, on the basis of the samples, computes
the approximation of the action-value function (learn-
ing phase) that is the solution of the control problem.
3.1 Batch Reinforcement Learning
Let us consider a system having a discrete-time dy-
namics. If the transition model or the reward function
are unknown, we cannot use dynamic programming
to solve the control problem. However, we suppose to
perform a sampling phase by which a set o samples
F = {< s(t)
i
,a(t)
i
,s(t + 1)
i
,r(t)
i
>,i = 1..K} (4)
is obtained from one or more system trajectories gen-
erated starting from an initial state, following a given
policy.
In the learning phase we used Fitted Q-iteration
(FQI, see (Ernst et al., 2005)) that reformulates value
function estimation as a sequence of regression prob-
lems by iteratively extending the optimization horizon
(Q
N
− f unction). First Q
0
(s,a) is set to 0 then the al-
gorithm iterates over the full sample set F . Given
the i-th sample < s(t)
i
,a(t)
i
,s(t + 1)
i
,r(t)
i
> and the
approximation of Q-function at time N (Q
N
), the es-
timation of Q
N+1
is performed by using Q-learning
update rule (Watkins, 1989):
Q
N+1
(s(t)
i
,a(t)
i
) = (1 − α)Q
N
(s(t)
i
,a(t)
i
)+
α(r(t)
i
+ γ max
a
0
∈A
Q
N
(s(t + 1)
i
,a
0
)). (5)
For each sample a new one is generated replac-
ing single step rewards with estimated Q-values.
This defines a regression problem from s(t)
i
,a(t)
i
to Q
1
(s(t)
i
,a(t)
i
) that enables the estimation of Q
1
.
Thereafter, at each iteration N, a new estimation is
performed exploiting the approximation at the previ-
ous iteration.
3.2 Q-function Approximation
Tree-based regression methods produce one or more
trees (ensemble) that are composed by a set of de-
cision nodes used to partition the input space. The
tree determines a constant prediction in each re-
gion of the partition by averaging the output val-
ues of the elements of the training set T S =
{(i
1
,o
1
),...,(i
#T S
,o
#T S
)} which belong to this re-
gion. Q-function are approximated by considering
i
l
=< s(t)
l
,a(t)
l
> while the output o
l
is the Q-value
of i
l
.
We used extremely-randomized tree ensem-
ble (Geurts et al., 2006), that is a regressor com-
posed by a forest of M trees each constructed by ran-
domly choosing K cut-points i
j
, representing the j-th
component of the action-state space, and the corre-
spondingly binary split [i
j
< t], representing the cut-
direction. The construction proceeds by choosing a
set of tests that maximizes a given score. The algo-
rithm stops splitting a node when the number of ele-
ments in the node is lower than a parameter n
min
.
4 PROBLEM DEFINITION
The state space of a dynamical system is defined by
the set of state variables that compound the ODE’s
system. System 1 in its canonical form (Savaresi
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
230

1k 2k 5k 10k 15k 20k 25k 30k 40k 50k
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
Fitted Q−Iteration comparison: N°samples vs NMin
Normalized performance index value
2
5
10
20
50
100
200
250
500
1000
N°Samples (k=1000)
NMin:
Vertical Body Velocity
(a)
1k 2k 5k 10k 15k 20k 25k 30k 40k 50k
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
Fitted Q−Iteration comparison: N°samples vs NMin
Normalized performance index value
2
5
10
20
50
100
200
250
500
1000
Vertical Body Acceleration
N°Samples (k=1000)
NMin:
(b)
Figure 2: Comparison of vertical body velocity (J
2
) and acceleration (J
1
) indexes w.r.t number of samples and NMin. J
1
and
J
2
are normalized by Mixed SH-ADD policy (J
1
= J
2
= 1).
et al., 2005) has 5 continuous state variables: S ≡<
˙z(t), ˙z
t
(t), ˙c(t),z(t) − ¯z,z
t
(t) − ¯z
t
>. The presence of
non-measurable road disturbances makes both the
transition model and the cost function stochastic.
Since not all the variables are measurable, BRL
policy is built exploiting the same sensor measures
as those used in the Mixed SH-ADD one (Savaresi
and Spelta, 2007): < ¨z(t), ˙z(t), ˙z(t) − ˙z
t
(t) >. The ac-
tion space contains only two values: A ≡< c
in
(t) >
|c
in
(t) ∈ {c
min
,c
max
}.
The minimization of the squared vertical acceler-
ations can be defined as the maximization of the fol-
lowing reward function:
R
1
(s(t),a(t)) = −¨z
2
(t + ∆T ). (6)
The ideal goal of a semi-active suspension system
is to negate the body vertical movements around its
steady state conditions, with respect to any road dis-
turbance. Thus, we considered also the following re-
ward:
R
2
(s(t),a(t)) = −˙z
2
(t + ∆T ) (7)
that aims to minimize the squared variation of the
body vertical velocity.
5 EXPERIMENTAL RESULTS:
ALGORITHM PARAMETERS
We performed a set of experiments in order to com-
pare performance with different parameterizations.
Samples are generated by controlling System (1) with
a random policy and by feeding it with a road dis-
turbance z
r
(t) designed as an integrated band-limited
white noise. This signal is a realistic approximation
of a road profile and excites all the system dynam-
ics (Hrovat, 1997). The number of samples ranges
from 1000 (10 seconds system simulation at 100Hz)
to 50000 (500 seconds simulation).
The optimization horizon has been fix to 10 since
it does not play a central role in this control prob-
lem. The number K of regressor’s cut points is set
to the dimension of the input space (in this case
K = |S| + |A| = 4, see (Geurts et al., 2006)) . The
number of trees depends mainly on the problem com-
plexity and ranges from 1 to 100 in our experiments.
Finally, the number of samples into a leaf, that affects
the regressor’s generalization ability, ranges from 2 to
1000. For each parameterization two cost functions
have been evaluated: J
1
and J
2
, which are obtained
by learning the control policy with R
1
and R
2
respec-
tively.
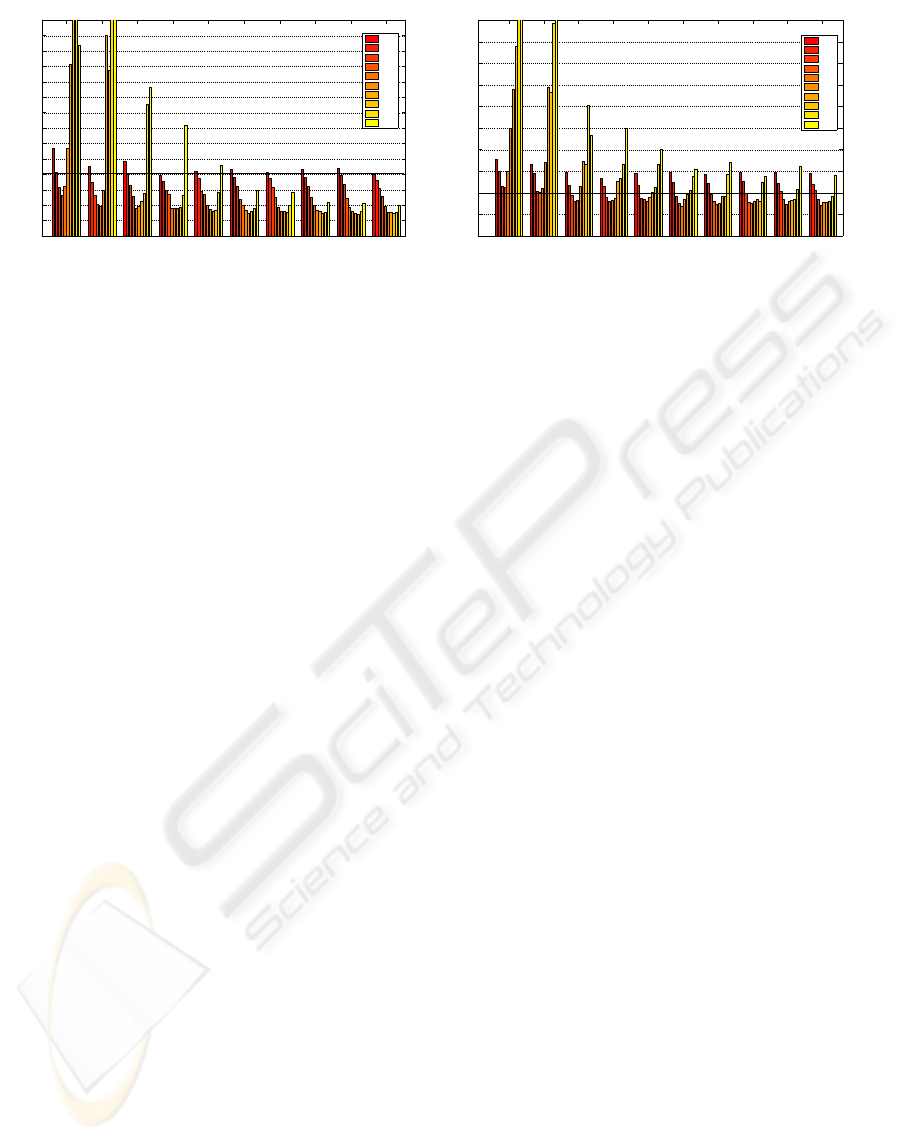
Figure 2 shows a comparison of policy obtained
by varying both the number of samples and the num-
ber of samples in a leaf (NMin). Cost function val-
ues are normalized by Mixed SH-ADD policy. Re-
sults showed that as the number of samples increases,
the cost decreases. Conversely, NMin and cost have
a quadratic relationship. Lower values of NMin lead
to over-fitting, larger values lead to a poor policy ap-
proximation, while intermediate values (NMin = 50)
obtained the best performance.
In Figure 3, a comparison of cost functions ob-
tained by varying both the number of samples and the
number of trees is presented. Again, index values are
normalized by the Mixed policy. The performance
improves by increasing both the number of samples
and the number of trees. Nonetheless, after a cer-
tain value (NTree >= 50) no significant cost reduc-
tion is observed, while the computational cost grows
linearly.
Figures 2 and 3 point out that the overall BRL-
policy behavior is better than Mixed SH-ADD one
on both indexes: J
1
and J
2
. The more samples we
have, the more accurate the learned policy will be.
Few samples can be used, but choosing NMin or trees
number can be critical.
BATCH REINFORCEMENT LEARNING - An Application to a Controllable Semi-active Suspension System
231

1k 2k 5k 10k 15k 20k 25k 30k 40k 50k
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2
Fitted Q−Iteration comparison: N°samples vs N°Trees
Normalized performance index value
1
2
5
10
20
30
50
80
100
200
N°Samples (k=1000)
N°Trees:
Vertical Body Velocity
(a)
1k 2k 5k 10k 15k 20k 25k 30k 40k 50k
0.8
0.85
0.9
0.95
1
1.05
1.1
1.15
1.2
1.25
1.3
1.35
1.4
1.45
1.5
Fitted Q−Iteration comparison: N°samples vs N°Trees
Normalized performance index value
1
2
5
10
20
30
50
80
100
200
N°Samples (k=1000)
N°Trees:
Vertical Body Acceleration
(b)
Figure 3: Comparison of vertical body velocity (J
2
) and acceleration (J
1
) indexes w.r.t number of samples and number of
trees. J
1
and J
2
are normalized by Mixed SH-ADD policy (J
1
= J
2
= 1).
(a) (b)
Figure 4: Graphical representation of Mixed SH-ADD and BRL policies projected on ¨z(t), ˙z(t) (a) and on ˙z(t), ˙z(t) − ˙z
t
(t)
(b).
6 EXPERIMENTAL RESULTS:
POLICY COMPARISON
The experiments of Section 5 identified good param-
eters value for the estimation of an optimal policy us-
ing the BRL technique: state space S
3
, action space
A, reward function R
2
(s(t),a(t)) (Equation 7), 50K
samples (500 seconds systems simulation), 10 fitted
horizon, 50 tress, 5 random splits and Nmin = 50.
BRL-policy is a multi-dimensional control
map that associates to every measurable state
< ¨z(t), ˙z(t), ˙z(t) − ˙z
t
(t) > a control action c
in
(t). A
graphical representation of this map is depicted in
Figure 4, where it is compared to the one obtained
by controlling the semi-active system with the Mixed
SH-ADD rule (quasi-optimal algorithm).
Figure 4 shows that BRL policy is very similar to
the one associated to the Mixed SH-ADD algorithm.
The BRL policy tends to prefer a high-damped sus-
pension. The main differences between BRL map
and Mixed SH-ADD can be highlighted around the
origin of the axis. However, notice that, in such a sit-
uation, any selected damping has small influences on
the body dynamics.
The performances of the semi-active suspension
system fed with a random signal z
r
(t) and ruled by
the BRL-policy has been evaluated in time and fre-
quency domain. The frequency domain analysis in
reported in Figure 5, which depicts the approximate
10
0
10
1
10
15
20
25
30
35
40
45
50
55
60
(Hz)
(dB)
Frequency response from road profile to body acceleration
α selector
ADD
BRL
LOW FREQUENCIES
HIGH FREQUENCIES
Mixed 2−sensors
Open Loop
(c
min
)
Open Loop
(c
max
)
SH
Figure 5: Frequency response from road profile to
vertical acceleration of different policies: c
max
, c
min
,
ADD,SH,Mixed SH-ADD and BRL-policy.
frequency response obtained as the ratio between the
power spectrum of the output ¨z(t) and the input z
r
(t).
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
232

c_max c_min SH ADD Mixed SH−ADD RL
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Comparison of performance indexes obtained by different policies
Normalized performance index value
J
2
=sum(ddz
2
)
J
1
=sum(dz
2
)
Figure 6: Comparison of different policies by using both
cost function J1 and J
2
.
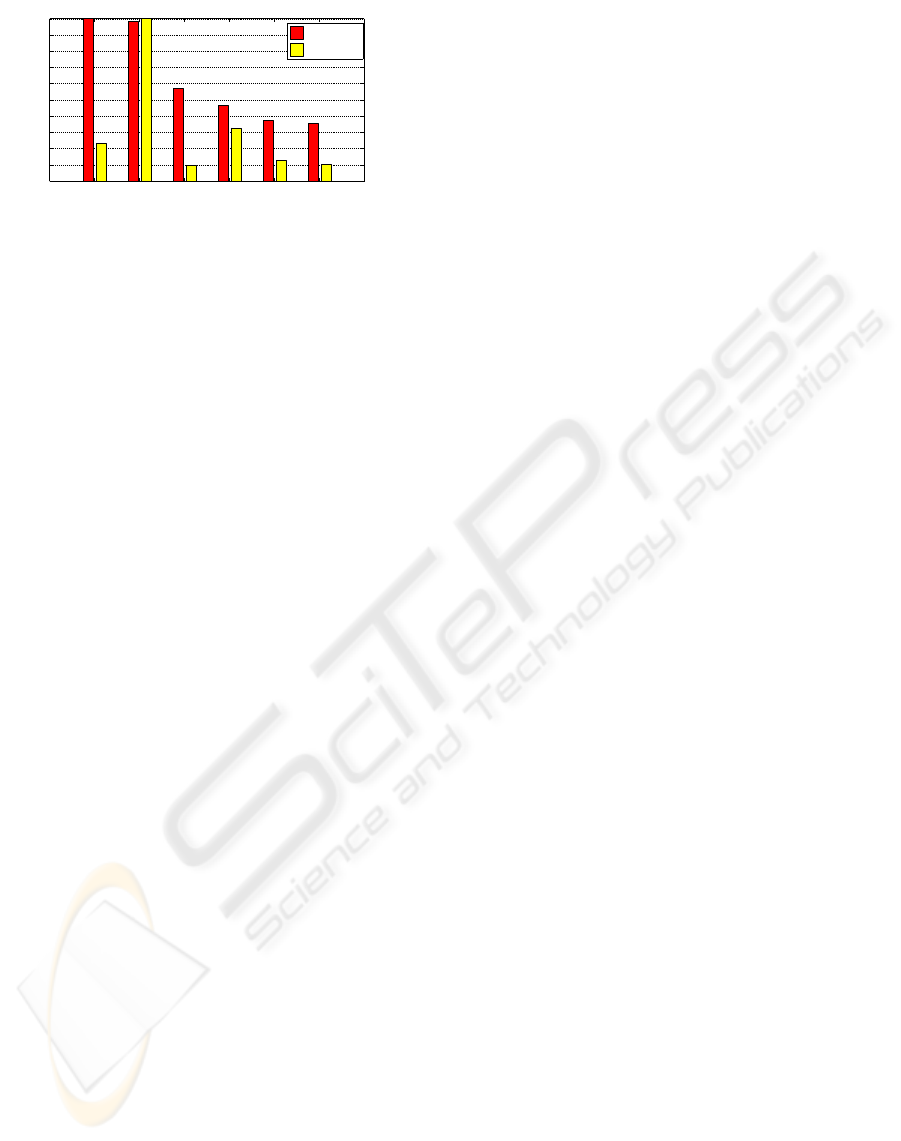
The time domain results are condensed in Figure 6
where the cost functions J
1
and J
2
are reported for dif-
ferent control strategies and compared to the extreme
passive configurations.
Figure 5 shows that BRL policy outperforms the
Mixed SH-ADD at low frequency. This is paid in
terms of filtering at high frequencies where Mixed
SH-ADD shows a better behavior. Figure 5 points
out that BRL policy provides the overall best perfor-
mance in terms of minimization of integral of squared
vertical body accelerations.
7 CONCLUSIONS
In this work we applied Batch Reinforcement Learn-
ing (BRL) to the design problem of optimal comfort-
oriented semi-active suspension which has not been
solved with standard techniques due to its complex-
ity. Results showed that BRL policy provides the best
results in terms of road disturbance filtering. However
the achieved performances are not far from the ones
obtained by the Mixed SH-ADD. Thus, comparing
the numerical approximation given by BRL, against
the analytical approximation given by the Mixed ap-
proach, we showed that they result in a similar strat-
egy. This is an important finding which shows how
numerical-based model-free algorithms can be used
to solve complex control problems. Since BRL tech-
niques can be applied to systems with unknown dy-
namics and are robust to noisy sensors, we expect to
obtain even larger improvements on real motorbikes,
as shown by preliminary experiments.
REFERENCES
Ahmadian, M., Reichert, B. A., and Song, X. (2001).
System non-linearities induced by skyhook dampers.
Shock and Vibration, 8(2):95–104.
Antos, A., Munos, R., and Szepesvari, C. (2008). Fitted
q-iteration in continuous action-space mdps. In Platt,
J., Koller, D., Singer, Y., and Roweis, S., editors, Ad-
vances in Neural Information Processing Systems 20,
pages 9–16. MIT Press, Cambridge, MA.
Ernst, D., Geurts, P., Wehenkel, L., and Littman, L. (2005).
Tree-based batch mode reinforcement learning. Jour-
nal of Machine Learning Research, 6:503–556.
Geurts, P., Ernst, D., and Wehenkel, L. (2006). Extremely
randomized trees. Machine Learning, 63(1):3–42.
Guardabassi, G. and Savaresi, S. (2001). Approximate lin-
earization via feedback - an overview. Survey paper
on Automatica, 27:1–15.
Hrovat, D. (1997). Survey of advanced suspension devel-
opments and related optimal control applications. Au-
tomatica(Oxford), 33(10):1781–1817.
Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996).
Reinforcement learning: a survey. Journal of Artificial
Intelligence Research, 4:237–285.
Karnopp, D. and Crosby, M. (1974). System for Controlling
the Transmission of Energy Between Spaced Mem-
bers. US Patent 3,807,678.
Riedmiller, M. (2005). Neural fitted q iteration - first experi-
ences with a data efficient neural reinforcement learn-
ing method. In ECML, pages 317–328.
Sammier, D., Sename, O., and Dugard, L. (2003). Sky-
hook and H8 Control of Semi-active Suspensions:
Some Practical Aspects. Vehicle System Dynamics,
39(4):279–308.
Savaresi, S., Silani, E., and Bittanti, S. (2005).
Acceleration-Driven-Damper (ADD): An Optimal
Control Algorithm For Comfort-Oriented Semiactive
Suspensions. Journal of Dynamic Systems, Measure-
ment, and Control, 127:218.
Savaresi, S. and Spelta, C. (2007). Mixed Sky-Hook and
ADD: Approaching the Filtering Limits of a Semi-
Active Suspension. Journal of Dynamic Systems,
Measurement, and Control, 129:382.
Savaresi, S. and Spelta, C. (2008). A single-sensor control
strategy for semi-active suspensions. To Appear, -:–.
Silani, E., Savaresi, S., Bittanti, S., Visconti, A., and
Farachi, F. (2002). The Concept of Performance-
Oriented Yaw-Control Systems: Vehicle Model and
Analysis. SAE Transactions, Journal of Passenger
Cars - Mechanical Systems, 111(6):1808–1818. ISBN
No.0-7680-1290-2,.
Sutton, R. and Barto, A. (1998). Reinforcement Learning:
An Introduction. MIT Press.
Valasek, M., Kortum, W., Sika, Z., Magdolen, L., and
Vaculin, O. (1998). Development of semi-active
road-friendly truck suspensions. Control Engineering
Practice, 6:735–744.
Watkins, C. (1989). Learining from Delayed Rewards. PhD
thesis, Cambridge University, Cambridge,England.
Williams, R. (1997). Automotive active suspensions Part
1: basic principles. Proceedings of the Institution of
Mechanical Engineers, Part D: Journal of Automobile
Engineering, 211(6):415–426.
BATCH REINFORCEMENT LEARNING - An Application to a Controllable Semi-active Suspension System
233