APPEARANCE-BASED DENSE MAPS CREATION

Comparison of Compression Techniques with Panoramic Images

Luis Payá, Lorenzo Fernández, Óscar Reinoso, Arturo Gil and David Úbeda

Departamento de Ingeniería de Sistemas Industriales, Miguel Hernández University

Avda. de la Universidad s/n. 03202, Elche (Alicante), Spain

Keywords: Robot Mapping, Appearance-based Methods, Omnidirectional Vision, Spatial Localization.

Abstract: The visual information captured by omnidirectional systems is very rich and it may be very useful for a

robot to create a map of an environment. This map could be composed of several panoramic images taken

from different points of view in the environment, and some geometric relationships between them. To carry

out any task, the robot must be able to calculate its position and orientation in the environment, comparing

his current visual information with the data stored in the map. In this paper we study and compare some

approaches to build the map, using appearance-based methods. The most important factor of these

approaches is the kind of information to store in order to minimize the computational cost of the operations.

We have carried out an exhaustive experimentation to study the amount of memory each technique requires

to build the map, and the time consumption to create it and to carry out the localization process inside it.

Also, we have tested the accuracy to compute the position and the orientation of a robot in the environment.

1 INTRODUCTION

When a robot or a team of robots have to carry out a

task in an environment, an internal representation of

it is usually needed so that the robot can estimate its

initial position and orientation and navigate to the

target points. Omnidirectional visual systems are a

widespread sensor used with this aim due to their

low cost and the richness of information they

provide. Extensive work has been carried out in this

field, using the extraction of some natural or

artificial landmarks from the images to build the

map and carry out the localization of the robot

(Thrun, 2003). However, these processes can be

carried out just working with the images as a whole,

without extracting landmarks nor salient regions.

These appearance-based approaches are useful

when working in unstructured environments where it

may be hard to create appropriate models for

recognition, and offer a systematic and intuitive way

to build the map. Nevertheless, as we do not extract

any relevant information from the images, an

important problem of such approaches is the high

computational cost they suppose.

Different researchers have shown how a

manifold representation of the environment using

some compression techniques can be used. A widely

extended method is PCA (Principal Components

Analysis), as (Kröse, 2004) does to create a database

using a set of views with a probabilistic approach for

the localization inside this database. Conventional

PCA methods do not take profit of the amount of

information that omnidirectional cameras offer,

because they cannot deal with rotations in the plane

where the robot moves. (Uenohara, 1998) studied

this problem with a set of rotated images, and

(Jogan, 2000) applied these concepts to an

appearance-based map of an environment. The

approach consists in creating an eigenspace that

takes into account the possible rotations of each

training image, trying to keep a good relationship

between amount of memory, time and precision of

the map. Other works rely on Fourier Transform to

compress the information, as (Menegatti, 2004), that

defines the concept of Fourier Signature and

presents a method to build the map and localize the

robot inside it, or (Rossi, 2008), that uses spherical

Fourier transform of the omnidirectional images.

The representation of an environment with

appearance-based approaches can be separated in a

low-level map, that represents a room with several

images and a high-level map, which tries to

modelize the spatial relationships between rooms

and between rooms and corridors. (Booij, 2007)

250

Payá L., Fernández L., Reinoso Ó., Gil A. and Úbeda D. (2009).

APPEARANCE-BASED DENSE MAPS CREATION - Comparison of Compression Techniques with Panoramic Images.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 250-255

DOI: 10.5220/0002210502500255

 SciTePress

shows how these concepts can be implemented

through a graph representation whose nodes are the

images and whose links denote similarity between

them and (Vasudevan, 2007) uses a hierarchy of

cognitive maps where place cells represent the

scenes through a PCA compression and the

information provided by a compass is used to

compute the connectedness between them.

Appearance-based techniques constitute a basis

framework to other robotics applications, as in

route-following, as (Payá, 2008) shows.

2 REVIEW OF COMPRESSION

TECHNIQUES USING

OMNIDIRECTIONAL IMAGES

In this section, we outline some techniques to extract

the most relevant information from a set of

panoramic images, captured from several positions

in the environment to map.

2.1 PCA-based Techniques

When we have a set of N images with M pixels each,

=ℜ∈

, each image can be transformed

in a feature vector (also named ‘projection’ of the

image)

;

ℜ∈ K1=

, being K the PCA

features containing the most relevant information of

the image,

≤

(Kirby, 2000). The PCA

transformation can be computed from SVD of the

covariance matrix C of the data matrix, X that

contains all the training images arranged in columns

(with the mean subtracted). If V is the matrix

containing the K principal eigenvectors and P is the

reduced data of size K x N, the dimensionality

reduction is done by , where the columns

of P are the projections of the training images,

XVP

·=

However, the database built in this way contains

information only for the orientation the robot had

when capturing each image but not for all the

possible orientations on each point. (Jogan, 2000)

presents a methodology to include this orientation

information but acquiring just one image per

position. When we work with panoramic images, we

can artificially rotate them by just shifting the rows.

This way, from every image

=ℜ∈

MxQ

ℜ

can build a submatrix where the first

column is the original image, and the rest of them

are the shifted versions of the original one, with a

∈X

rotation between them.

When having a set of N training images, the data

matrix is composed of N blocks, and the covariance

matrix has the following form:

[

]

⎥

⎦

⎤

⎢

⎣

⎡

==⇒

NNNN

XXX

XXC

MOMM

22221

11211

XXXX

(1)

Where are circulant blocks. The

eigenvectors of a general circulant matrix are the Q

basis vectors from the Fourier matrix (Ueonara,

1998):

QxQik

ℜ∈X

()

[

]

iQii

−

γγγω

1,,,,0

−===

−

jeQi

(2)

This property allows us to compute the

eigenvectors without necessity of performing the

SVD decomposition of C (this would be a

computationally very expensive process). This

problem can be solved by carrying out Q

decompositions of order N. The eigenvectors of C

shall be found among vectors of the form:

[

]

Niv

iii

,,0,,,,

ωαωαωα

(3)

where

[

]

iiii

,,0,,,,

αααα

are the

eigenvectors of the following matrix:

⎥

⎦

⎤

⎢

⎣

⎡

=Λ

iii

λλλ

MOMM

22221

11211

(4)

where is an eigenvalue of

corresponding to

the eigenvector

. As the matrix has N

eigenvectors, if we repeat this process for every

we can obtain Q·N linearly independent eigenvectors

of C.

2.2 Fourier-based Techniques

2.2.1 2D Discrete Fourier Transform

When we have an image f(x,y) with N

rows and N

columns, the 2D discrete Fourier Transform is

defined through:

APPEARANCE-BASED DENSE MAPS CREATION - Comparison of Compression Techniques with Panoramic Images

251

()

[]

()

1,,0,1,,0

−=−=

⋅=

==ℑ

∑∑

−

⎟

⎠

⎞

⎜

⎝

⎛

+−

NvNu

eyxf

vuFyxf

(5)

The components of the transformed image are

complex numbers so it can be split in two matrices,

one with the modules (power spectrum) and other

with the angles. The most relevant information in the

Fourier domain concentrates in the low frequency

components. Furthermore, removing high frequency

information can lead to an improvement in

localization because these components are more

affected by noise. Another interesting property when

we work with panoramic images is the rotational

invariance, which is reflected in the shift theorem:

()

[]

()

1,,0,1,,0

−=−=

⋅=−−ℑ

⎟

⎠

⎞

⎜

⎝

⎛

+⋅−

NvNu

evuFyyxxf

(6)

According to this property, the power spectrum

of the rotated image remains the same of the original

image and only a change in the phase of the

components of the transformed image is produced,

whose value depends on the shift on the x-axis (x

)

and the y-axis (y

). It means that when two images

are acquired from close points of the environment

but with different headings for the robot, then, the

power spectrum is very similar, and studying the

difference in phases we could estimate the angle

between the two orientations, using eq. (6).

2.2.2 Fourier Signature of the Image

If we work with panoramic images, we can use

another Fourier-based compact representation that

takes profit of the shift theorem applied to

panoramic images (Menegatti, 2004). It consists in

expanding each row of the panoramic image

{

}

{

}

110

,,,

−

aaaa K

using the Discrete Fourier

Transform into the sequence of complex numbers

{

}

{

}

110

,,,

−

This Fourier Signature presents the same

properties as the 2D Fourier Transform. The most

relevant information concentrates in the low

frequency components of each row, and it presents

rotational invariance. However, it exploits better this

invariance to ground-plane rotations in panoramic

images. These rotations lead to two panoramic

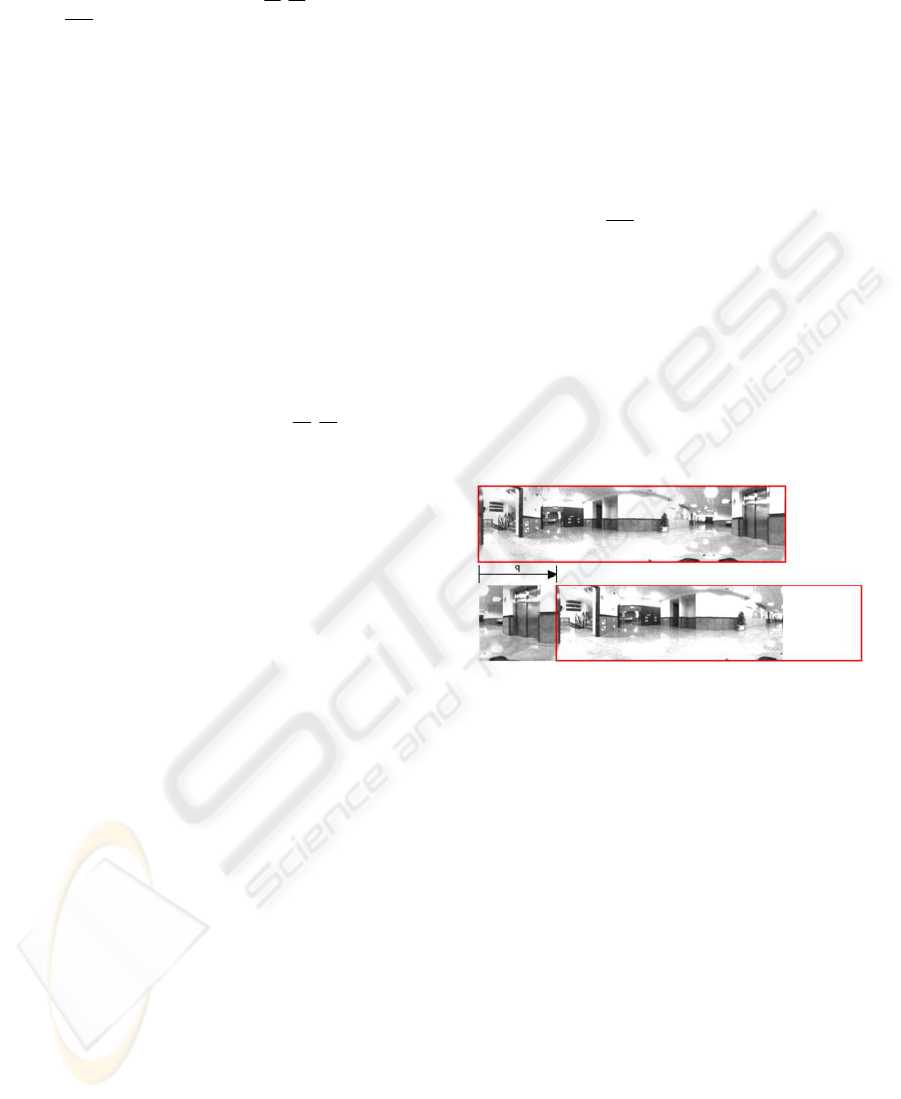
images which are the same but shifted along the

horizontal axis (fig. 1). Each row of the first image

can be represented with the sequence

{

and each

row of the second image will be the sequence

}

{

}

−

being q the amount of shift, that is proportional to

the relative rotation between images. The rotational

invariance is deducted from the shift theorem, which

can be expressed as:

{}

[]

1...,,0;

−==ℑ

⋅−

− y

kqn

NkeAa

(7)

where

{

}

[

]

−

ℑ

is the Fourier Transform of the

shifted sequence, and are the components of the

Fourier Transform of the non-shifted sequence.

According to this expression, the amplitude of the

Fourier Transform of the shifted image is the same

as the original transform and there is only a phase

change, proportional to the amount of shift q.

Figure 1: A robot rotation on the ground plane produces a

shift in the panoramic image captured.

3 MAP BUILDING

To carry out the experiments, we have captured a set

of omnidirectional images on a pre-defined 40x40

cm grid in an indoor environment, including an

unstructured room (a laboratory) and a structured

one (a corridor). We work with panoramic images

with size 56x256 pixels. Once we have all the

panoramic images, we have used the compression

methods exposed in the previous section. Fig. 2(a)

shows a bird’s eye view of the grid used to take the

images and two examples of panoramic images.

Before using the compression methods, a

normalisation and a filtering process have been

carried out to make the map robust to changes in

illumination. There have been significant differences

when using each one of the compression methods,

regarding the elapsed time and the amount of

memory the map takes up once it is built.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

252

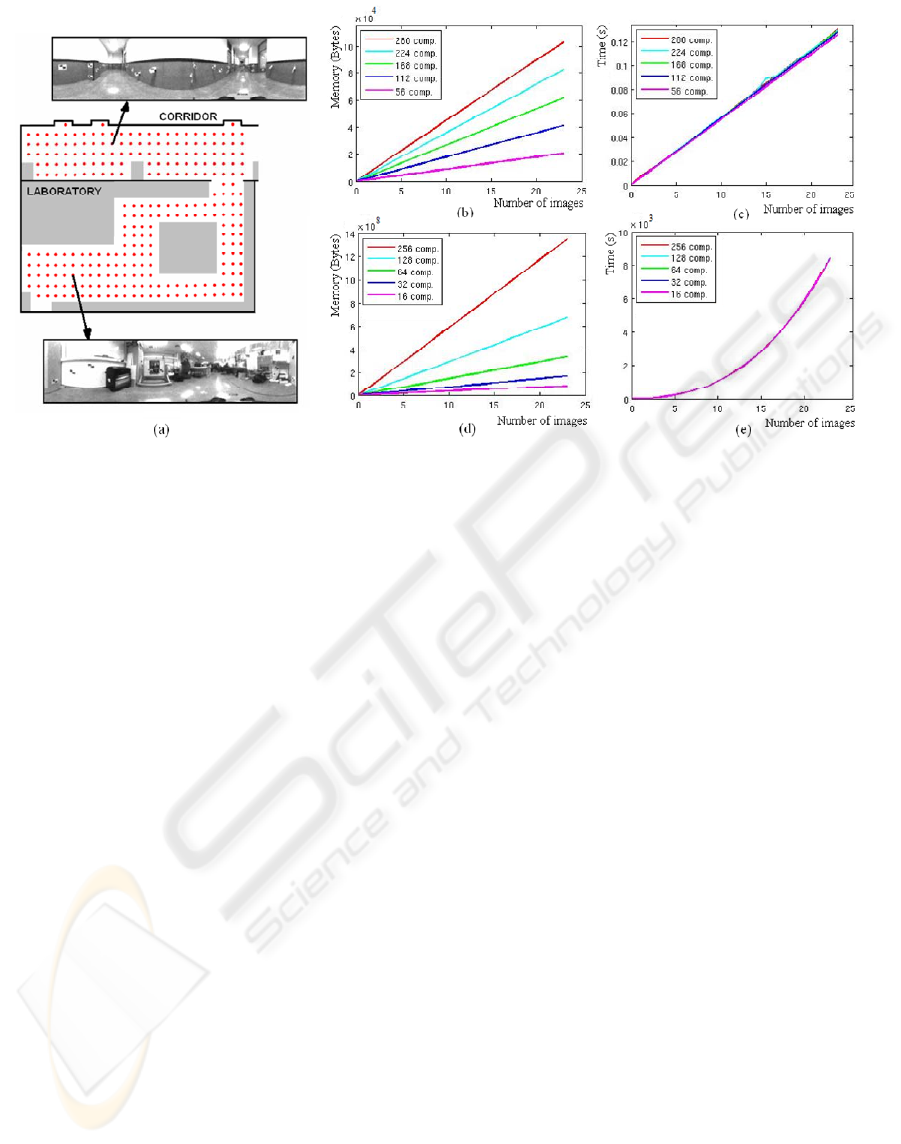
Figure 2: (a) Grid used to capture the training set of images, (b) amount of memory taken up and (c) time elapsed to build

the map with the Fourier-based approaches, (d) amount of memory and (e) time elapsed with the PCA-based approach.

Fig. 2(b) shows the amount of memory the map

constructed takes up, depending on the number of

images in the map, and the number of Fourier

Components we retain (those of lower frequency).

When we work with the Fourier Signature, taking

224 components implies we retain 4 Fourier

Components per row (56 rows in the image). In the

case of 2D Fourier transform, 224 components

means we take the firs 7 rows and 32 columns

(where the main information is concentrated).

Fig. 2(c) shows the elapsed time to build the

database, depending on the number of images in the

map and the number of Fourier components we

retain. The time elapsed is very similar when we use

the Fourier Signature and the 2D Fourier Transform.

On the other hand, fig. 2(d) and 2(e) show the results

when using the PCA compression technique for

spinning images. Fig 2(d) shows the amount of

memory required. The PCA map is composed of the

matrix

CV ∈

, which contains the K main

eigenvectors and the projections of the training

images

;

∈ K1=

Although the training images have been

artificially rotated to add the orientation information

in the database, it is not necessary to store the

projections of all the rotated images but only the

projections of one image per training position. This

is due to the fact that a rotation in the image results

in the change of angle of the PCA coefficients of

this image, but not in the module. So, if we have the

coefficients for one representative viewpoint, the

coefficients of the rotated images can automatically

be generated through a rotation in the complex

plane. So the module of the projections can be used

to compute the position of the robot, and the phase is

useful to know the orientation. Anyway, as we can

see on fig. 2, PCA is a computationally more

expensive process comparing to Fourier Transform.

4 LOCALIZATION AND

ORIENTATION RECOVERING

To test the validity of the previous maps, the robot

has captured several test images in some half-way

points among those stored in the map. We have

captured two sets of test images, the first one, at the

same time we took the training set and the second

one a few days later, in different times of the day

(with varying illumination conditions) and with

changes in the position of some objects. The

objective is to compute the position and orientation

of the robot when it took the test images, just using

the visual information in the maps.

4.1 PCA-based Techniques

The PCA map is made up of the matrix

∈

which contains the K main eigenvectors and the

projections of the training images

∈

(one per

position, as explained in the previous section), that

APPEARANCE-BASED DENSE MAPS CREATION - Comparison of Compression Techniques with Panoramic Images

253

have been decomposed in two vectors,

∈

containing the modules of the components of the

projections and

∈

containing the phases.

To compute the location where the robot took

each test image, we have to project the test image

onto the eigenspace,

1Mxi

Rx ∈

Kxi

Cx ∈

Vp =

Then, we compute the vector of modules

1Kxi

Rp ∈

and compare it with all the vectors

stored in the

map. The criterion used is the Euclidean distance.

The corresponding position of the robot is extracted

as the best matching. Once this position is known,

we make use of the phases vector

to compute

the orientation of the robot.

Table 1 shows the results we have obtained

when computing the position and the orientation

when the training set is taken over a 30x30 cm grid

and table 2 shows the same results for an 40x40 cm

grid, depending on the number of eigenvectors (K)

we retain. In these tables, p

is the probability that

the best match is the actually nearest image

(geometrically), p

is the probability that the best

match is one of the two actually nearest images, and

is the probability it is one of the three nearest

images. At last, e

is the average error in the

orientation estimation.

Table 1: Accuracy in the estimation of the position and

orientation with PCA methods. 30x30 cm grid training set.

112

81.8 96.7 97.1 3.21º

224

82.6 96.8 98.8 2.89º

448

87.2 96.8 98.8 5.29º

Table 2: Accuracy in the estimation of the position and

orientation with PCA methods. 40x40 cm grid training set.

112

96.3 97.1 98.4 8.07º

224

96.7 97.5 99.3 5.95º

448

97.9 98.8 99.5 4.79º

Fig. 3(a) shows the time taken up by this method

to compute the position and orientation, depending

of the number of images stored in the map, and the

number of eigenvectors.

4.2 Fourier-based Techniques

To compute the position and orientation of the robot

for each test image, we compute the Fourier

Transform (with the two methods described in the

previous section) and then, we compute the

Euclidean distance of the power spectrum of the test

image with the spectra stored in the map. The best

match is taken as the current position of the robot.

On the other hand, the orientation is computed

with eq. (6), when we work with 2D Discrete

Fourier Transform (assuming y

= 0) and with the

expression (7), when we work with the Fourier

Signature. We obtain a different angle per row so we

have to compute the average angle. Tables 3 and 4

show the accuracy we obtain in position and

orientation estimation with the Fourier methods.

Table 3: Accuracy in the estimation of the position and

orientation. Fourier methods. 30x30 cm grid training set.

2x56

76.5 94.6 96.3 3.13º

4x56

78.5 95.5 97.5 3.04º

8x56

83.9 97.4 98.4 2.91º

16x56

85.5 98.4 98.4 2.89º

Table 4: Accuracy in the estimation of the position and

orientation. Fourier methods. 40x40 cm grid training set.

2x56

94.2 96.7 97.2 4.36

4x56

94.6 97.5 98.3 4.35

8x56

96.7 98.8 100 4.40

16x56

97.5 99.6 100 4.37

Fig. 3(b) shows the time elapsed since the robot

captures the omnidirectional image until the position

and orientation of the robot are obtained, depending

on the number of images stored in the map and the

number of Fourier components we retain. This

approach clearly outperforms the PCA methods in

accuracy and time consumption.

(a) (b)

Figure 3: Time consumption to compute position and

orientation with (a) PCA and (b) Fourier methods.

5 CONCLUSIONS

In this work, we have exposed the principles of the

creation of a dense map of a real environment, using

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

254

omnidirectional images and appearance-based

methods. We have presented three different methods

to compress the information in the map. The

mathematical properties of these methods together

with the rich information the omnidirectional images

pick up from the environment permit the robot to

compute its position and orientation into the map.

The Fourier Transform method (both the 2D

Discrete Fourier Transform and the Fourier

Signature) has proved to be a good method to

compress the information comparing to PCA

regarding both the time and the amount of memory,

and the accuracy in position and orientation

estimation. Another important property is that the

Fourier Transform is an inherently incremental

method. When we work with PCA, we need to have

all the training images available before carrying out

the compression so this method cannot be applied to

tasks that require an incremental process (e.g. a

SLAM algorithm where the information of the new

location must be added to the map while the robot is

moving around the environment). The Fourier

Transform does not present this disadvantage

because the compression of each image is carried

out independently. These properties make it

applicable to future tasks where the robots have to

add new information to the map and localize

themselves in real time.

This work opens the door to new applications of

the appearance-based methods in mobile robotics.

As we have shown, the main problem these methods

present is the high requirements of memory and

computation time to build the database and make the

necessary comparisons to compute the position and

orientation of the robot. Once we have studied in

deep some methods to compress the information and

separate the calculation of position and orientation,

the next step should be to test their robustness to

changes in illumination and in the position of some

objects in the scene. Also, their robustness and

simplicity make them applicable to the creation of

more sophisticated maps, where we have no

information of the position the robot had when he

took the training images.

ACKNOWLEDGEMENTS

This work has been supported by the Spanish

government through the project DPI2007-61197.

‘Sistemas de percepción visual móvil y cooperativo

como soporte para la realización de tareas con redes

de robots’.

REFERENCES

Artac, M.; Jogan, M. & Leonardis, A., 2002. Mobile

Robot Localization Using an Incremental Eigenspace

Model, In Proceedings of IEEE International

Conference on Robotics and Automation, Washington,

USA, pp. 1205-1030, IEEE.

Booij, O., Terwijn, B., Zivkovic, Z., Kröse, B., 2007.

Navigation using an Appearance Based Topological

Map. In IEEE International Conference on Robotics

and Automation, pp. 3297-3932 IEEE Press, New

York.

Jogan, M., Leonardis, A., 2000. Robust Localization

Using Eigenspace of Spinning-Images. In Proc. IEEE

Workshop on Omnidirectional Vision, Hilton Head

Island, USA, pp. 37-44, IEEE.

Kirby, M., 2000. Geometric data analysis. An empirical

approach to dimensionality reduction and the study of

patterns, Wiley Interscience.

Kröse, B., Bunschoten, R., Hagen, S., Terwijn, B.

Vlassis, N., 2004. Household robots: Look and learn.

In IEEE Robotics & Automation magazine. Vol. 11,

No. 4, pp. 45-52.

Menegatti, E.; Maeda, T. Ishiguro, H., 2004. Image-based

memory for robot navigation using properties of

omnidirectional images. In Robotics and Autonomous

Systems. Vol. 47, No. 4, pp. 251-276.

Payá, L., Reinoso, O., Gil, A., Sogorb. J., 2008. Multi-

robot route following using omnidirectional vision and

appearance-based representation of the environment.

In Lecture Notes in Artificial Intelligence. Hybrid

Artificial Intelligence Systems, Vol. 5271, pp. 680-687

Springer.

Rossi, F., Ranganathan, A., Dellaert, F., Menegatti, E.,

2008. Toward topological localization with spherical

Fourier transform and uncalibrated camera. In Proc.

Int. Conf. on Simulation, Modeling and Programming

for Autonomous Robots. Venice (Italy), pp. 319-330.

Thrun, S., 2003. Robotic Mapping: A Survey, In

Exploring Artificial Intelligence in the New Milenium,

pp. 1-35, Morgan Kaufmann Publishers, San

Francisco, USA.

Ueonara, M., Kanade, T, 1998. Optimal approximation of

uniformly rotated images: relationship between

Karhunen-Loeve expansion and Discrete Cosine

Transform. In IEEE Transactions on Image

Processing. Vol. 7, No. 1, pp. 116-119.

Vasudevan, S., Gächter, S., Nguyen, V., Siegwart, R.,

2007. Cognitive maps for mobile robots – an object

based approach. In Robotics and Autonomous Systems.

Vol. 55, No. 1, pp. 359-371.

APPEARANCE-BASED DENSE MAPS CREATION - Comparison of Compression Techniques with Panoramic Images

255