A HYBRID METAHEURISTIC FOR SOLVING

SINGLE MACHINE SCHEDULING PROBLEM

Adrian Serbencu, Viorel Mînzu, Daniela Cernega and Adriana Serbencu

Control Systems and Industrial Informatics Department “Dunarea de Jos”Galati University

Domneasca – 47, Galati, Romania

Keywords: Discrete optimization, Manufacturing, Metaheuristics, Stochastic descent, Ant Colony Systems.

Abstract: This paper proposes a metaheuristic for solving the Single Machine Scheduling Problem that is

implemented by a hybrid system made up of an Ant Colony System and a stochastic descent algorithm

called Kangaroo. The hybrid system is based on the collaboration between a social type multiagent system

and an Iterated Solution Improvement method.

1 INTRODUCTION

The main purpose of multiagent systems is the

distributed solving of problems. A special type of

problem, which can be solved in a distributed way,

is the combinatorial optimization problem. The idea

of the algorithm “ant system” (Dorigo, et al., 1996)

has the source in the study of insects collective

behavior. The ants have the capability to act together

in order to perform a task, but any of them could not

perform alone the task (Beckers, et al., 1992). This

is a distributed solving mechanism because every

agent has only a very small contribution. The

complex collective behavior and the interactions

between agents are fundamental in the field of

artificial life.

This paper proposes a metaheuristic for solving

the Single Machine Scheduling Problem (SMSP).

For a given processor and a set of jobs that must be

executed on this processor, the problem is to

determine the sequence of jobs such that the

weighted tardiness (defined in section 2) is

minimized. Obviously, because of the combinatorial

aspect, this kind of problem is NP-complete. Hence,

sub-optimal solutions are generally preferred to

optimal ones. A sub-optimal solution is given by an

approximation algorithm like genetic algorithm,

simulated annealing, tabu search, stochastic descent

algorithms, etc. In paper (Madureira, et al., 2000),

an interesting practical resolution is given, in the

context of a scheduling system for Dynamic Single

Machine Problem. The SMSP is solved using a

genetic algorithm and thus, good results are

obtained.

In exchange, algorithms like simulated annealing

(Kirkpatrick, et al., 1983), tabu search (Gloverf,

1989), stochastic descent (Papadimitriou and

Steiglitz, 1982), etc. are Iterated Solution

Improvement methods, which means that only one

solution is improved by an iterative procedure. This

kind of methods has abilities to intensify the local

search and to detect the local minima. In the last

years, hybrid metaheuristics (Vaessens, et al, 1992;

Taillard et al., 1998; Mahfoud, and Goldberg, 1995)

have been developed, giving very interesting results.

That is why, this paper proposes an Ant Colony

System (ACS) based metaheuristic, described in

section 3, formed by an ACS and a parallel version

of a stochastic descent algorithm, called Kangaroo.

The system has the collaborative power of the ACS

and the intensification ability of the Kangaroo

algorithm (KA).

The paper is organized as follows. In section 2,

the Single Machine Scheduling Problem is stated.

The general structure of the proposed hybrid system

is presented in section 3 and the particularities of an

ACS solving the SMSP are described in section 4.

Section 5 outlines the implementation of the

Kangaroo Algorithm, whereas the computational

results are presented in section 6.

Serbencu A., Mînzu V., Cernega D. and Serbencu A. (2009).

A HYBRID METAHEURISTIC FOR SOLVING SINGLE MACHINE SCHEDULING PROBLEM.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,

pages 68-74

DOI: 10.5220/0002210700680074

 SciTePress

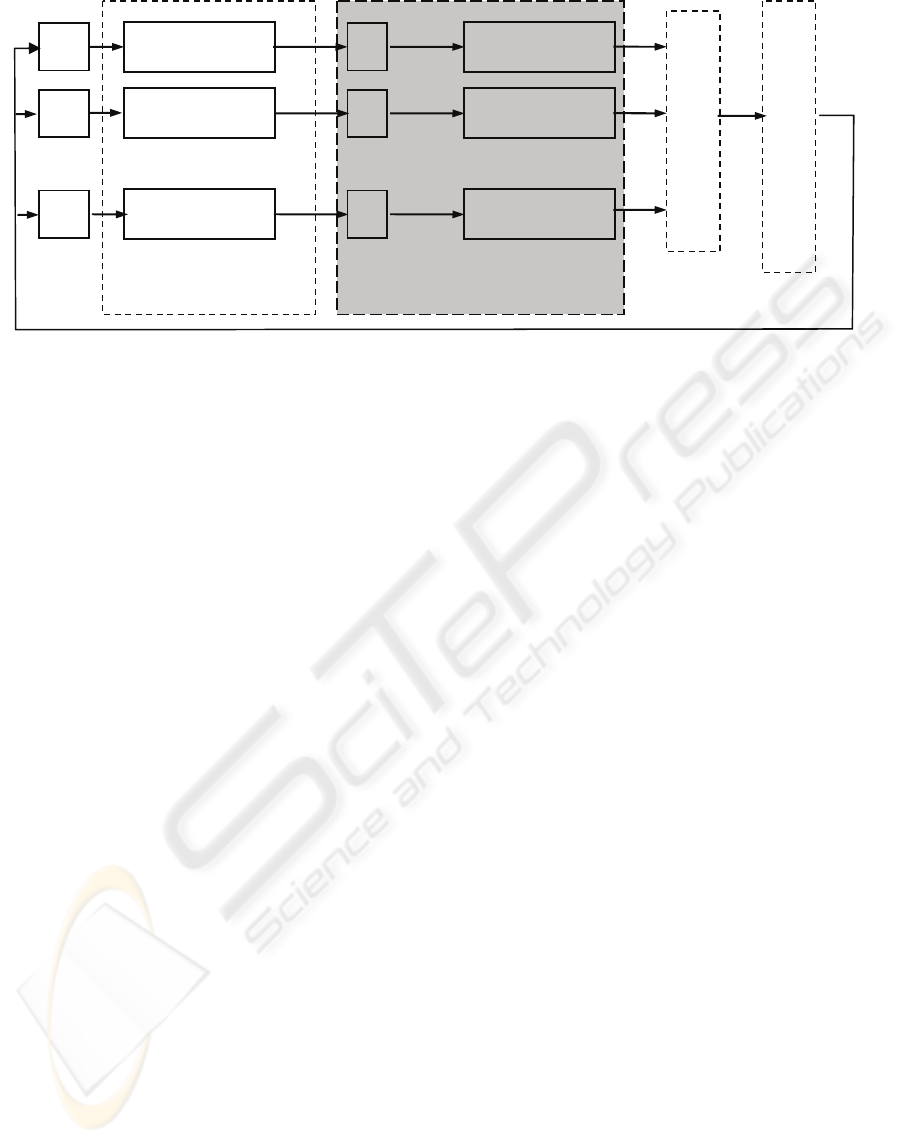
Figure 1: Ant Colony System with Kangaroo algorithm.

2 SINGLE MACHINE

SCHEDULING PROBLEM

In order to minimize the total Weighted Tardiness

for the SMSP the following assumptions are

considered: a set of n independent jobs (j= 1,…,n) is

available for processing at time zero and the

attributes of the jobs are known in advance. The

machine is never kept idle if there are any jobs to

complete and it can handle only one job at a time. It

processes the jobs without pre-emption. The jobs’

set-up times are independent of the jobs' sequence,

being included in the job processing times.

For each job j, it is considered p

the processing

time, d

the due date, that means the date when the

job should be completed, and w

the penalty liable

for each unit of delay. The jobs’ completion starts at

time t=0. The tardiness of a job is given by

{

}

jjjj

TMaxtpd=+−,

where t

is the start time of job j. The objective

function, which will be referred as fitness function,

is:

()

uwT

∑

where u is a solution of the problem, that is a

permutation of the job set:

12 ii1 n

u [ j , j , ..., j , j , ..., j ]

{

}

j 1,2,...,n∈

The optimality criterion of the SMSP is

min ( )

This problem is a combinatorial optimization

NP-complete problem. The problem can't be solved

with deterministic optimal algorithms, as they

require a computational time that increases

exponentially with the problem size (Garey, and

Johnson, 1979).

3 AN ANT COLONY SYSTEM

BASED METAHEURISTIC

In papers (Bauer, et al., 1999; Matthijs, et al., 2000)

the Ant Colony System is used to solve SMSP. In

this approach, the artificial ants are constructing

solutions for this problem and afterwards these

solutions are considered initial solutions for a local

optimization procedure.

The main idea of the proposed metaheuristic is to

use a stochastic descent method instead of the local

optimization procedure. In fact, this method is an

Iterated Solution Improvement metaheuristic called

Kangaroo. As a result, we have a special hybrid

metaheuristic based on the collaboration between a

social multiagent system - Ant Colony System - and

a parallel version of Kangaroo algorithm.

The ACS is made up of N artificial ants which

are constructing solutions of the optimization

problem. The ants communicate using structured

variables whose values represent a provisional

quotation of the solutions or of parts of solutions

quality. The value of these structured variables

simulates the "pheromone" allowing the

communication between ants in natural systems. In

this case, the structured variables are grouped in a

"pheromone" matrix.

The general optimization system is an iterative

searching process for a better solution of the given

problem. An iteration has two succesive phases. In

Parallel version of

Solution construction &

Solution selection

Solution

’

Solution

’

Solution

’

Ant

Global

heromone u

date

A HYBRID METAHEURISTIC FOR SOLVING SINGLE MACHINE SCHEDULING PROBLEM

the first phase, ACS is constructing N solutions and

the "pheromone" is continuously updated. The

resulting solutions are taken over in the second

phase, in order to be improved, by N instances of the

KA. From the beginning, the KA makes a local

optimization using the solutions produced by each

ant as initial solutions. The KA is not limited to this

single action, but it keeps trying to improve the

current solution following its own strategie. Every

instance of the KA is also an iterative procedure

looking for a better solution than the current one, in

a prescribed number of iterrations. The best found

solution is selected and it will be used in a new

global "pheromone" updating phase.

In the next iterration, the informations

accumulated in the "pheromone" matrix will be used

by the ACS, to guide the construction of the new set

of solutions. Here after, an outline of the proposed

metaheuristic is presented.

Figure 2: General structure of the proposed metaheuristic.

As mentioned before, at the first step, the

"pheromone" matrix is also updated during the

solutions construction (see section 4). The stop

criterion is usually a certain number of iterations.

4 ANT COLONY SYSTEM FOR

SOLVING SMSP

Generally speaking, for solving a combinatorial

optimization problem ACS needs two kinds of

information(Dorigo, et al., 1996; Dorigo, and

Gambardella, 1997a; Dorigo, and Gambardella,

1997b). One of them is the heuristic information and

the other one is specific to the ACS and concerns the

"pheromone".

Each ant of ACS produces a solution of the

problem, in the step 1 of the algorithm. This solution

is a complete sequence of jobs obtained by an

iterative process of placing a job j on the position i

(Matthijs, et al., 2000). At the position i, the ant

chooses the job j meeting two constraints:

a) the job j is not already placed in the sequence and

b) the "pheromone" τ(i, j) has the maximum value

for the job j.

For SMSP, the "pheromone" τ(i,j) is a quotation

of the interest to place a job j on the position i. The

heuristic information considered by an ant aiming to

select a job for the current position may be

represented by the inverse of the due date, or the

Modified Due Date (MDD)( Bauer, et al., 1999)

computed with the formula

max{d , (C )}

mdd p=+,

where C is the total processing time of the jobs

already placed.

An ant k will select with probability q

the most

attractive job, in order to be placed in the current

position i, that is the task j assuring the maximum of

[][]

τ(, ) η(, )ij ij⋅ . Nevertheless, the same ant may

choose with the complementary probability (1-q

) a

job j using the probabilistic rule

[][]

uJ()

0otherwise

τ(, ) η(, )

if J ( )

τ(, ) η(, )

p(, )

ij ij

∈

⋅

∈

⋅

⎧

⎪

⎨

⎪

⎩

∑

(1)

where:

- q

is a parameter of the algorithm

(, )

mdd

is the heuristic

information

- J

(i) is the set of not yet placed job by ant k;

- β is a parameter which determines the relative

importance of heuristic information

(0)

> .

When all the artificial ants have constructed the

solutions, the algorithm uses the following rule for

the global updating of the pheromone matrix:

(, ) (1 ) (, ) (, )ij ij ij

ατ α τ

←

−⋅ +⋅Δ (2)

where

f ( , ) best sequence

(, )

0otherwise

Tiij

−

∈

Δ=

⎧

⎨

⎩

- 0<α<1 is the pheromone increase parameter

- T is the total weighted tardiness of the global-best

solution from the beginning of the trial.

The application of the rule (2) enforces only the

1. The Ant Colony System constructs N

solutions for the given problem;

2. The parallel version of Kangaroo

Algorithm uses the N solutions

from the first step as initial

solutions and begins N stochastic

descent processes. The result is

a set of N other better solutions;

3. Select the best solution from this

set and use it to update the

"pheromone" matrix;

until the stop criterion.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

pheromone belonging to the best solution

encountered until the current iteration. This is the

reason of a premature convergence of the algorithm.

Therefore, the rule of local pheromone updating is

used. Every time the pheromone information is used

by an ant selecting the job j for the position i, the

rule (3) modeling the natural process of pheromone

evaporation (forgetting) is applied:

(, ) (1 ) (, ) (, )ij ij ij

ρτ ρ τ

←− ⋅ +⋅Δ (3)

where 0<ρ<1 is a parameter.

The term Δ

(i, j) in our implementation is set to

, the initial pheromone level. In order to calculate

, our algorithm constructs an initial solution for

SMSP. In this solution, the jobs are placed in

increasing order of the due date. The value of τ

initialized with the inverse of the total weighted

tardiness of this solution.

5 KANGAROO ALGORITHM

The KA is an approximation technique based on

stochastic descent (Fleury, 1995), inspired by the

simulation annealing method, but having a quite

different searching strategy.

The "Kangaroo" method is implemented by an

iterative procedure which minimizes an objective

function f(u). A current solution u of the considered

problem is replaced by a better one, situated in its

neighborhood N(u), using a random selection. The

algorithm tries "A" times to improve the current

solution, where A is a parameter of the algorithm. If

a new improvement is no longer possible, a "jump"

procedure is performed, in order to escape from the

attraction of a local minimum. This time the

improvement of the current solution is not

compulsory. This procedure can use a different

neighborhood definition N'(u).

A detailed description of the KA is given in

Minzu, and Henrioud, 1998. The stop criterion is

either a maximum iteration number or a bottom

bound of the objective function.

The best solution u

encountered in the iterative

process is memorized. At the end of KA, u* is the

"optimal" solution proposed by the algorithm.

The neighborhood N(u) is the set of solution u'

obtained from u by the permutation of the jobs

placed on positions i and i+1. For example, if u=[1 4

3 2 5], it holds N(u)={[4 1 3 2 5], [1 3 4 2 5], [1 4 2

3 5], [1 4 3 5 2], [5 4 3 2 1]}.

When a new improvement of the current solution

is no longer possible u is replaced by a solution u'

given by the "jump" procedure. In the case of SMSP

a possible definition of the neighborhood N'(u) is the

whole search space, but the KA converges (with

probability 1) slowly to the global optimum. A very

important aspect is the fact that deterministic

heuristics may be integrated in "jump" procedure, in

order to guide the search of an optimum solution

keeping the convergence of the KA if the

accessibility constraint is met (Minzu, and Henrioud,

1998). That is why, in the case of SMSP the

neighborhood N'(u) may be the set of solution u'

obtained from u by permutation of the job placed on

max

position, where i

max

is the position in u of the job

max

where

Twj

,...,1

max

maxarg

, with a job placed

on position i<i

max

. So the "jump" procedure

determines the job with the biggest weighted

tardiness and replaces it with a job situated on its

left. In this way there is a chance to diminish the

value of the criterion f(u).

6 IMPLEMENTATION AND

COMPUTATIONAL RESULTS

In order to reduce the run time of the hybrid system,

the job selection rule is applied on a reduced

candidate list that does not contain all the unplaced

Table 1: Computational results of the stand-aloneACS.

Problem Optimal

value

Best value Deviation of

the Best Value

Wt100-1 5988 8795 47

Wt100-2 6170 7724

Wt100-3 4267 5672

Wt100-4 5011 6426

Wt100-5 5283 7709

Wt100-6 58258 76424

Wt100-7 50972 83231

Wt100-8 59434 90968

Wt50-1 2134 2832

Wt50-2 1996 2557

Wt50-3 2583 2583

Wt50-4 2691 3278

Wt50-5 1518 2568

Wt50-6 26276 34167

Wt50-7 11403 13668

Wt50-8 8499 9713

Wt40-1

913 913 0

Wt40-2

1225 1431 17

Wt40-3

537 537 0

Wt40-4

2094 2163 3

Wt40-5

990 1090 10

Wt40-6 6955

8151 17

Wt40-7 6324

9083 44

Wt40-8 6865

11474 67

A HYBRID METAHEURISTIC FOR SOLVING SINGLE MACHINE SCHEDULING PROBLEM

Table 2: Computational results with the hybrid system.

Problem

Optimal

value

Best

ACS

value

Best value of ACS+KA with:

M=1000

M=2000

M=5000

M=10000

Deviation

Best value

eviation%

Computing

time[s]

Best

value

Deviation

Computing

time[s]

Wt100-1 5988 8795

6310

5.38

1.906

6314 6076 1.47

8.609

6215 3.79

Wt100-2 6170 7724

6450 4.54 1.906

6182 6182 0.19

8.641

6182 0.19

Wt100-3 4267 5672

4415 3.47 1.938

4336 4372 2.46

8.688

4297 0.70

Wt100-4 5011 6426

5094 1.66 1.922

5014 5058 0.94

8.797

5069 1.16

Wt100-5 5283 7709

5433 2.84 1.938

5435 5283 0.00

8.703

5367 1.59

Wt100-6 58258 76424

60445 3.75 2.063

63804 63341 8.72

9.516

59845 2.72

Wt100-7 50972 83231

52349 2.70 2.063

55788 54822 7.55

9.484

53063 4.10

Wt100-8 59434 90968

62907 5.84 2.063

62146 62636 5.39

9.469

62817 5.69

Wt50-1 2134 2832

2134 0.00 1.063

2134 2134 0.00

4.891

2134 0.00

Wt50-2 1996 2557

1998 0.10 1.078

2009 2011 0.75

4.953

2008 0.60

Wt50-3 2583 2583

2619 1.39 1.078

2583 2583 0.00

5.031

2583 0.00

Wt50-4 2691 3278

2691 0.00 1.078

2691 2691 0.00

5.000

2691 0.00

Wt50-5 1518 2568

1518 0.00 1.078

1518 1604 5.67

5.031

1518 0.00

Wt50-6 26276 34167

27077 3.05 1.188

26758 26509 0.89

5.500

26403 0.48

Wt50-7 11403 13668

11403 0.00 1.156

11522 11733 2.89

5.375

11403 0.00

Wt50-8 8499 9713

8700 2.36 1.156

8760 8742 2.86

5.375

8700 2.36

Wt40-1 913 913

913 0.00 0.891

913 913 0.00

4.188

913 0.00

Wt40-2 1225 1324

1225 0.00 0.922

1225 1225 0.00

4.250

1225 0.00

Wt40-3 537 573

537 0.00 0.922

537 537 0.00

4.281

537 0.00

Wt40-4 2094 2098

2094 0.00 0.922

2094 2094 0.00

4.281

2094 0.00

Wt40-5 990 1090

990 0.00 0.906

990 990 0.00

4.203

990 0.00

Wt40-6 6955 12949

7024 0.99 0.984

6955 7055 1.44

4.609

6955 0.00

Wt40-7 6324 7087

6636 4.93 1.000

6324 6437 1.79

4.609

6571 3.91

Wt40-8 6865 11015

6919 0.79 1.000

6881 6919 0.79

4.594

6901 0.52

jobs at the current iteration. This list is updated

dynamically for each step and each ant. Every ant

keeps a copy of the best found solution until the

current iteration. Each time the ant adds a new job j

to the current sequence, this job is deleted from the

copy of the best found solution. In our

implementation, the first 20 jobs, which belong to

the best solution and that are not already placed,

form the candidate list.

Computational tests were performed in order to

compare the proposed hybrid system (ACS+KA)

with a stand-alone ACS. The software developed

was coded in C and the tests were performed on a

PC with 2330 MHz Intel processor.

The two algorithms were applied to the same

instances of SMSP. Three sets of 8 problems each

with 40 (Wt40-x, x=1,…,8), 50 (Wt50-x, x=1,…,8),

and 100 (Wt100-x, x=1,…,8) jobs were considered.

Consequently, for both, the stand-alone ACS and the

hybrid system, the computational tests were done on

a set of 24 instances of the SMSP. These problems

were downloaded from the site

http://people.brunel.ac.uk/~mastjjb/jeb/orlib/files/,

which supplies data and the optimal solution for

some Single Machine Scheduling Problems.

The parameters used by the ACS in the two systems

are: N=10, q

=0.9, α=0.9, β=2. The two systems

evolved on the same number of iterations. Hence,

the stop criterion (see fig. 2) was an upper limit for

the general number of iterations. In this case this

upper limit was 100.

The results obtained using only the stand-alone

ACS for the 3 sets of problems are presented in table

1. The "optimal value" column contains the value of

the optimization criterion for the optimal solution of

the problem. For a given instance of SMSP, this

value is generally unknown. The "best value" is the

value of the optimization criterion for the best

solution produced by the stand-alone ACS. The last

column gives the deviation of the best value from

the optimal one expressed in percents.

The hybrid system ACS+KA ran also over 100

general iterations, but with different values for the

number of iterations, denoted M, of the stochastic

searching process implemented by KA in each step 2

of the general algorithm (see fig. 2). The results are

shown in Table 2.

Four values for M were considered: 1000, 2000,

5000, 10000. The deviation of the best

solution from the optimal one is given only for

M=5000 and M=10000 iterations. With M=10000

iterations, the hybrid system finds the optimal

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

solution in almost all the cases.

Despite the fact this number of iterations doesn't

take much time, it is not necessary to adopt such a

great number of iterations.

Let's remark we are interested in obtaining a good

solution and not the optimal one, especially since it

is unknown. Because the deviation is satisfactory for

M=5000, this number of iterations is recommended

for SMSP with 100 jobs. The same conclusion may

to be drawn both for 40 or 50 jobs problems. The

value of M may decrease, with very satisfactory

results, to 1000 or 2000 iterations.

Comparing the two tables, one can see that the

hybrid system is more efficient. Despite the fact the

stand-alone ACS evolves during 100 iterations, it

doesn't reach the same results as the hybrid system.

When M=5000, the price to pay is the very

acceptable increasing of the execution time, that

means 5, 6 or 10 seconds for 40, 50 or 100 jobs

problems, respectively.

The table 3 shows a comparison between the hybrid

system ACS+KA and the earliest due date algorithm

(EDD).

Table 3: Comparison between EDD and ACS+KA.

Problem EDD ACS+KA

M=5000

Best

value

Deviation

Best

value

Deviation

Wt100-1 14138 136.11

6076 1.47

Wt100-2 19096

209.50

6182 0.19

Wt100-3 17538

311.01

4372 2.46

Wt100-4 13308

165.58

5499 9.74

Wt100-5 20218

282.70

5283 0.00

Wt100-6 13932

139.16

63341 8.72

Wt100-7 16009

214.08

54822 7.55

Wt100-8 16534

178.19

62636 5.39

Wt50-1 7306

242.36

2134 0.00

Wt50-2 7219

261.67

2011 0.75

Wt50-3 4983

92.92

2583 0.00

Wt50-4 6423

138.68

2691 0.00

Wt50-5 6257

312.19

1604 5.67

Wt50-6 57699

119.59

26509 0.89

Wt50-7 41718

265.85

11733 2.89

Wt50-8 43030

406.29

8742 2.86

Wt40-1

1588 73.93

913 0.00

Wt40-2

5226 326.61

1225 0.00

Wt40-3

3051 468.16

537 0.00

Wt40-4

5527 163.94

2094 0.00

Wt40-5

4030 307.07

990 0.00

Wt40-6 23691

240.63

7055 1.44

Wt40-7 33547

430.47

6437 1.79

Wt40-8 23032

235.50

6919 0.79

One can see that the deviation of EDD is

unsatisfactory and the solution obtained with this

algorithm can be only an initial solution for a more

efficient algorithm, like ACS+KA.

7 CONCLUSIONS

The paper has proposed a metaheuristic for solving

SMSP, implemented by a hybrid system made up of

an Ant Colony System and a parallel version of the

Kangaroo Algorithm.

The KA is a very simple and efficient intensifier

that replaces the local optimization proposed in other

papers.

The functioning of this hybrid system was

compared with a stand-alone ACS. The tests have

proven that this structure is more efficient than those

of the simple ACS. The number of general iterations

and the iterations number of the stochastic descent

process are parameters of the algorithm that have to

be tuned according to the size of the problem. Very

good solutions were found in a quite acceptable time

and number of iterations. Moreover, the increasing

of the execution time is quite acceptable.

REFERENCES

Bauer A., Bullnheimer B., Hartl R.F. And Strauss C.,

1999. An ant colony optimization approach for the

single machine total tardiness problem, In Proc. of

CEC’99, pages 1445–1450, IEEE Press, Piscataway,

NJ,.

Beckers R., Deneubourg J.L., And Goss S., 1992. Trails

and U-turns in the selection of the shortest path by the

ant Lasius Niger, Journal of Theoretical Biology, vol.

159, pp. 397–415.

Dorigo, M., Maniezzo V. And Colorni A., 1996. The Ant

System: Optimization by a colony of cooperating

agents, IEEE Transactions on Systems, Man, and

Cybernetics–Part B, 26, 29–41,

Dorigo M. And Gambardella L.M., 1997a. Ant colonies

for the traveling salesman problem, BioSystems, 43,

73–81.

Dorigo M. And Gambardella L.M., 1997b. Ant colony

system: A cooperative learning approach to the

traveling salesman problem, IEEE Transactions on

Evolutionary Computation, 1(1):53-66.

Fleury G., 1995. Application des méthodes stochastiques

inspirées du recuit simulé à des problèmes

d'ordonnancement, Automatique Productique

Informatique Industrielle vol. 29-no 4-5, pp. 445-470.

Garey M; Johnson D. ,1995. Computers and Intractability:

a guide to the theory on NP-completeness- New York

W. H. Freeman and Co. Publishers.

A HYBRID METAHEURISTIC FOR SOLVING SINGLE MACHINE SCHEDULING PROBLEM

Gloverf, 1989. Tabu Search- part i. ORSA Journal of

Computing vol. 1 1989 pp. 190-206.

Kirkpatrick S. et all, 1983 -Optimization by simulated

annealing- Science vol.220 no.4598 May 1983 pp 671-

680

Madureira A. Et All, 2000. A GA Based Scheduling

System for Dynamic Single Machine Scheduling

Problem, ISATP 2000, Fukuoka.

Mahfoud S.; Goldberg D, 1995. Parallel recombination

simulated annealing: A genetic algorithm. Parallel

computing vol. 21 1995 pp. 1-28.

Matthijs Den Besten, Stützle T. And Dorigo M., 2000 Ant

Colony Optimization for the Total Weighted Tardiness

Problem, In Deb et al, editors, Proceedings of PPSN-

VI, Sixth International Conference on Parallel

Problem Solving from Nature, volume 1917 of LNCS,

pages 611-620.

Minzu V. And Henrioud J.M, 1998. Stochastic algorithm

for the tasks assignment in single or mixe model

assembly lines, European Journal of Automation, Vol.

32 No 7-8, pp 831-851.

Papadimitriou C.; Steiglitz K., 1982. Combinatorial

Optimization: Algorithms and Complexity - Printice-

Hall.

Taillard et al., 1998. La programmation à mémoire

adaptative ou l'évolution des algorithmes évolutifs.

Calculateurs parallèles vol. 10 no. 2 April 1998 pp.

117-140.

Vaessens R. et al, 1992. A local search template. Parallel

Problem Solving From Nature R. Manner and B.

Manderick Edition Université Libre de Bruxelles pp.

67-76 Belgium.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics