POSITION CONTROL OF A SERVO-PNEUMATIC SYSTEM
Hybrid Fuzzy P+I Controller of a Servo-Pneumatic Fatigue Simulator
Marco Santos, Jorge Ferreira
Department of Mechanical Enginnering, University of Aveiro, Campus Universitário de Santiago, Aveiro, Portugal
José Simões
Department of Mechanical Enginnering, University of Aveiro, Aveiro, Portugal
Keywords: Servo-pneumatics, Fuzzy control, PI control, Hybrid fuzzy P+I control, High position accuracy,
Biomechanical devices, Fatigue tests, Instrumented hip joint prosthesis.
Abstract: This paper proposes a hybrid fuzzy P+I controller for a servo-pneumatic machine to perform and monitor
tests on biomechanical devices, such as orthopaedic prosthesis. The methodology followed is based upon
the CompactRIO®, a real-time platform, and the system was fully programmed using LabVIEW language.
Separate algorithms of a PI, proportional fuzzy and hybrid fuzzy P+I controllers were developed and
compared. The performance of the overall system has already been tested and the experimental results for
position control show that the PI controller can reach 2 µm of accuracy but with a very slow rise time.
However, the same accuracy can be achieved with Hybrid Fuzzy P+I controller, although with a fast rise
time and neglected overshoot. The authors can conclude that this proposal can successfully overcome
unknown nonlinear parameters of the pneumatic system and has high position control accuracy.
1 INTRODUCTION
More than 250000 surgeries of total knee
replacement and 180000 surgeries of total hip
replacement are performed in the US every year.
The smart hip joint prosthesis is a new research
field, which is integrated in the Biomechanics
Research Group (University of Aveiro) strategy.
Total Hip Replacement (THR) arthroplasty is
currently one of the most performed elective surgical
procedures. The most serious complication of THR
is loosening of the prosthetic stem and cup. No
technique is capable of determining with exactness
the levels of loosening, the reasons and the regions
of the implant were it occurs with time. It has been
referred that more than 80% of the non-successes are
due to implant loosening. In this context, the
PTDC/EME-PME/70824/2006 project, still running,
has been financed, whose main aim is to develop a
cemented and instrumented hip prosthesis with
sensorial capacities to detect the degree of implant
loosening and the regions where it occurs with time,
through a non-invasive method that can be used to
define clinical correction and prevention
methodologies. Therefore, medical staff could
access to “continuous” information about the
evolution of the implant behaviour, providing means
to avoid the presence of patients frequently in the
medical office. The work here presented is mainly
related with the project presented above and with an
ongoing project where the principal aim is to
develop a methodology to produce and study ultra
high molecular weight polyethylene reinforced with
carbon nanotubes (CNT/UHMWPE composites) and
evaluate its suitability for enhancing the wear
resistance of acetabular cups and therefore
minimizing the above highlighted issues.
This background drew the need to develop a high
position control and force accuracy of a 1 degree-of-
freedom (DOF) servo-pneumatic machine developed
by Biomechanics Research Group of the University
of Aveiro (Santos, et al., 2008) to carry out the
required fatigue simulation tests or any kind of
pneumatic force up to 3 kN. The control system must
also be prepared/easily fitted to answer to the
accuracy requirements related with new researches
on smart implants which may occur in the future.
The fatigue simulator is shown in figure 1.
234
Santos M., Ferreira J. and Simões J. (2009).
POSITION CONTROL OF A SERVO-PNEUMATIC SYSTEM - Hybrid Fuzzy P+I Controller of a Servo-Pneumatic Fatigue Simulator.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,
pages 234-239
DOI: 10.5220/0002210802340239
Copyright
c
 SciTePress

2 MECHANICAL APPARATUS
The main purpose of the fatigue simulator is the
simulation of biomechanical actions to the static and
dynamic characterization of synthetic femurs and
tibias, with and without prostheses. This goal
requires the tracking of positional reference
trajectories through an upright course, as well as
force references. An aluminum frame structure was
reinforced to give more stability. The movement of
the cylinder’s piston and the load cell were protected
with two lateral linear guides to compensate
asymmetric loads. This press has already been used
to perform long time running fatigue tests for more
than 2 weeks running non-stop.
Figure 1: Mechanical Apparatus.
3 INSTRUMENTATION
The servo-pneumatic system consists of:
- A double effect pneumatic cylinder (Festo
CRDNGS-80-200-PPV-A) with a 200 mm length
and 80 mm diameter to ensure 3016 N at 6 bar;
- A servo-valve (Festo MPYE-5-1/8-HF-010-B) with
750 l/min capacity, to establish the amount of air
circulating in each of the two actuator’s chambers;
- An optical linear scale (Fagor SV- B220) with
resolution of 1 µm is used to measure the machine’s
actuator moving mass.
- A load cell (AEP TC4), with 10 kN capacity and
0.1% resolution of that value, is used to measure the
applied force to the biomechanical device.
4 HARDWARE PLATFORM
The National Instruments PAC CompactRIO
®
ensures the interface and the connection between the
control software and all the instrumentation devices.
It is constituted by a Reconfigurable CompactRIO
®
Intelligent Real-Time Controller/Web Server NI
cRIO-9002, a four-slot reconfigurable embedded
chassis NI cRIO-9103, a 16 bit Analog Input NI
cRIO-9215, a Digital Input NI cRIO-9411 and a 16
bit Analog Output NI cRIO-9263. The real-time
controller NI cRIO-9002 has its own 195 MHz
industrial processor, 32 MB DRAM memory and a
FTP server. With its embedded LabVIEW real-time
ETS and a reconfigurable Field Programmable Gate
Array (FPGA), this platform makes possible the
development of high speed deterministic control
applications with high flexibility.
5 SOFTWARE PLATFORM
All the control, monitor and data acquisition
software were implemented using LabVIEW 8.0
Professional Development System and LabVIEW
Reconfigurable Software Development Kit (includes
LabVIEW Real-Time 8.0 and LabVIEW FPGA 8.0
modules), to ensure the controller autonomy, the
easy interface with the user operator, the possibility
of remote web monitoring and the easy upgrade of
controllers. The hardware platform allows a three
layer distributed software, as shown in figure 2.
Previous work on the design of position and force
controllers using this platform were conducted by
Santos et al. (Santos, et al., 2008).
Figure 2: Three layer distributed software.
POSITION CONTROL OF A SERVO-PNEUMATIC SYSTEM - Hybrid Fuzzy P+I Controller of a Servo-Pneumatic
Fatigue Simulator
235

6 THE PNEUMATIC SYSTEM
The pneumatic servosystem represented in figure 3,
is composed by a pneumatic cylinder, which
performs movement, and a 5/3 servovalve, that
modulates the amount of air entering the cylinder.
P
i
, T
i
and A
i
represent pressure, temperature and
piston areas of chambers i. M is the actuator moving
mass and x is its position. The air supply pressure P
s
is set at 6 bar. The servovalve and the pneumatic
cylinder are the two system’s main blocks.
Pneumatic systems usually present a set on
nonlinearities that creates problems to close loop
controllers. When high accuracy positioning tasks is
requested, electrical solutions are normally chosen
instead of servopneumatic solutions. The complexity
in controlling servopneumatic systems is mainly due
to the air compressibility, the piston friction and the
non-linear behaviour of the servovalve. In the
present case, the servovalve is the highly nonlinear
element of the servopneumatic system. The
assumption that the orifices area of the servovalve
varies linearly with the command input can lead to
large modelling errors near the spool central
position. Furthermore, there is also the temperature
and pressure dynamics of the actuator chambers that
should not be neglected (Carneiro, 2006).
Figure 3: Pneumatic Servosystem.
7 THE CONTROL SYSTEM
The general positioning accuracy in pneumatic
control systems only can reach to the range from
±0.1 mm to ±0.05 mm. Xiang and Wikander (Xiang,
2004) and Carneiro (Carneiro, 2007) have achieved
positioning errors below 5 µm, through the
application of nonlinear control methodologies
based in the information from mathematical models
of the system, respectively feedback linearization
and sliding mode control, to deal with the
nonlinearities of the pneumatic system. However,
they also have to deal with the inaccuracy of the
mathematical model, because it cannot perfectly
represent all possible dynamics of the physical
process. So, the control system performance depends
on the mathematical model accuracy. And cannot be
forgotten that the application of some nonlinear
control techniques requires lower-order “design
models”. To deal with these problems, Pai and Shih
(Pai, et al., 2003) have developed a fuzzy PD
controller and they’ve got a positioning accuracy of
20 nm (equal to the resolution of the linear digital
scale), the best experimental result found in the
literature by the authors. They used heuristic
information to build a “human-in-the-loop”
controller and have written down a set of rules on
how to control the process. Then, they incorporated
them into a fuzzy controller to emulate their
decision-making process. They have defined the
error and change of error as inputs, one output and
only nine rules; mamdani control rules and the
maximum-minimum algorithm; and “center of the
gravity” defuzzification method. They don’t detail
neither about the linear digital scale nor the 3/5-port
proportional control valve. The control system was
only tested with step and small multi-step inputs.
As opposed to “conventional” control approaches,
where the focus is on modelling and the use of the
model to build a controller, the fuzzy control is
concerned about the intuitive understanding of how
to best control the process (Passino, et al., 1998).
The performances of a PI and fuzzy logic closed
loop control strategies have been studied. Finally, a
hybrid fuzzy-P+I controller was implemented to take
the advantages of both (Liu, et al, 2007).
7.1 PI Control
The development of a PI controller requires finding
the appropriate proportional and integral parameters
K
P
and K
i
, respectively, as shows in Equation 1.
dt)t(eK)t(eK)t(u
t
0
iP
∫
+=
(1)
Because of the limited displacement of the
pneumatic and the related integral component
evolution, an anti-windup technique is used to
introduce a dead zone between non-saturated output
values (Carneiro, 2007). The optimized parameters
found were K
p
=100 and K
i
=10.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
236

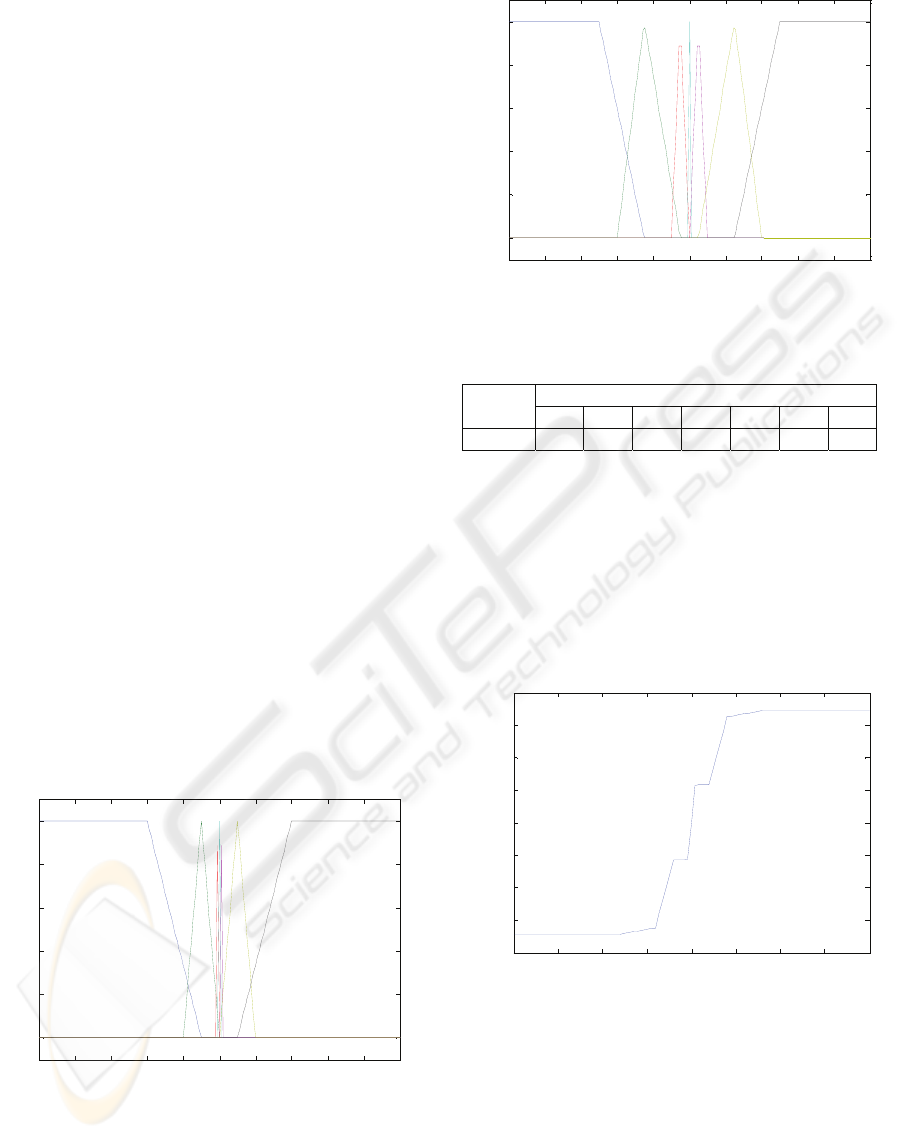
7.2 Fuzzy Control
The Fuzzy Logic Control (FLC) is based on an
input-output function that maps each numerical
input to a low-resolution quantization interval and
calculates the control signal based on an output
quantization interval (Ferreira, et al., 2006). The
input values for the position fuzzy feedback control
were the position error. Seven membership functions
were defined for the error and the same number to
the output signal, as shown in the program code
below (transcribed from .fis file) and in figures 4 and
5. Table 1 shows the base-rule. Mamdani control
rules and maximum aggregation method are applied.
The rule's weight was set equal to 1. The “center of
the gravity” method is used to defuzzify and to get
the accurate control signal.
[Input1] Name='error’
Range= [-1 1]
MF1='-3': [-1 -1 -0.4 -0.1]
MF2='-2': [-0.2 -0.1 0]
MF3='-1': [-0.02 -0.01 0]
MF4='0': [0 0 0]
MF5='1': [0 0.01 0.02]
MF6='2': [0 0.1 0.2]
MF7='3': [0.1 0.4 1 1]
[Output1] Name='signal'
Range= [-1 1];
MF1='-3': [-1 -1 -0.5 -0.25]
MF2='-2': [-0.4 -0.25 -0.05]
MF3='-1': [-0.1 -0.05 0]
MF4='0': [0 0 0]
MF5='1': [0 0.05 0.1]
MF6='2': [0.05 0.25 0.4]
MF7='3': [0.25 0.5 1 1]
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
error
Degree of membership
-3 -2 -1012 3
Figure 4: Membership function of the position error.
The saturation limits of the position error were set to
-200 and 200 mm. The accuracy of the
approximation depends mostly on the membership
functions and the rules.
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
signal
Degree of membership
-3 -2 -1 0 1 2 3
Figure 5: Membership function of the control output.
Table 1: Fuzzy Rule matrix.
Error
-3 -2 -1 0 1 2 3
Signal -3 -2 -1 0 1 2 3
The optimized control system response can also be
seen as a non-linear operation function shown in
Figure 6. It models the servovalve opening/closing
rate µ
FUZZY
as a function of the position error. This
design has the behaviour of a fuzzy proportional
(FP). It is the simplest “human-in-the-loop”
controller, although must link the requirements of
high accuracy, fast rise time and neglected overshoot
results with an easy control system parameterization.
-200 -150 -100 -50 0 50 100 150 20
0
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
Position Error
Servovalve Response
Figure 6: Operation function of the FP controller.
Many researchers have been studying the
architecture of fuzzy controllers. On-line processing
of the fuzzy inference rules requires high
computational processing cost. Several authors
proposed a controller in which the values of the
membership functions must be fixed before
computation of the control process and showed that
the fuzzy algorithm can be converted into matrices
to represent the parameterized fuzzy model. One of
POSITION CONTROL OF A SERVO-PNEUMATIC SYSTEM - Hybrid Fuzzy P+I Controller of a Servo-Pneumatic
Fatigue Simulator
237

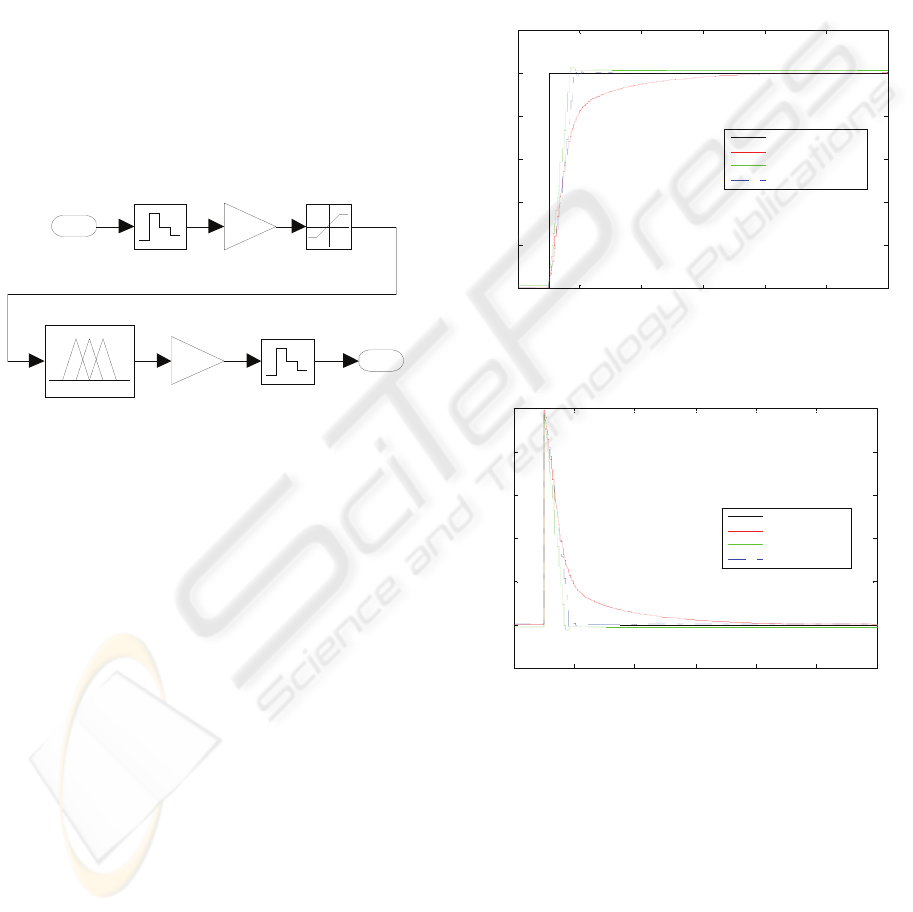
the advantages of a matrix representation is that its
computation is faster than the fuzzy control
statements. To carry out a real-time computing
system with CompactRIO
®
Controller using the
fuzzy logic controller, a 1D Look-up Table is
generated from the Fuzzy Logic toolbox in Matlab.
Once a value for the position error is found, it is
cross-referenced in the Look-Up Table to find the
control output. The selected parameters which create
the table were intervals of 0.02 for the position error.
For inputs values between these intervals, the output
value is established by linear interpolation. So, this
algorithm is run off-line and the generated table is
sent to cRIO-9002 though FTP protocol. The closed
loop control was design into the Real-Time
Controller. The LabVIEW block diagram is shown
in Figure 7. The optimized parameters were K
e
=1
and K
s
=1.
1D Look -up Table
Control
Output
1
Zero -Order
Hold 2
Zero -Order
Hold 1
Saturation
Gain 2
Ks
Gain 1
Ke
Fuzzy Logic Controller
Position
Error
1
Figure 7: LabVIEW block Diagram of the Fuzzy Logic
Controller.
7.3 Hybrid Fuzzy P+I Control
Fuzzy controllers do not need precise information
about the nonlinearities of the system to be effective.
However, it is useful the use of the integral of the
error to deal with steady-state error of the position
variable, which is difficult to eliminate only with the
developed FLC. Hence, it was developed a hybrid
system where it was given a weight of 91,5% to the
fuzzy logic controller and a weight of 8,5% to the
integrator contribution, in order to achieve its
optimized performance. Equation 2 shows the hybrid
Fuzzy P+I control law.
dt)t(eK085.0915.0)t(u
t
0
iFUZZY
∫
+= μ
(2)
The optimized value of K
i
is 10. An anti-windup
technique is also used.
8 EXPERIMENTAL RESULTS
All the control algorithms presented in section 7
were built-in into cRIO-9002 Controller and
compared. Several step signals were applied as the
position reference in the control experiments and the
cylinder position measurements were recorded.
Figures 8 and 9 show the system response when
each of the control methods is applied with a step
signal reference from 0 to 100 mm.
0 1 2 3 4 5 6
0
20
40
60
80
100
120
Time(s)
Position (mm)
Position Reference
PI Control
Fuzzy Control
Fuzzy-PI Control
Figure 8: Step signal response curves of PI, Fuzzy and
Hybrid Fuzzy-P+I Controllers.
0 1 2 3 4 5 6
-20
0
20
40
60
80
100
Time(s )
Position Error (mm)
Error Reference
PI Control
Fuzzy Control
Fuzzy-PI Control
Figure 9: Step signal error curves of PI, Fuzzy and Hybrid
Fuzzy-P+I Controllers.
The
steady-state position error between actual
position and the set point value is 1,104 mm for FP
controller and 2 µm for Hybrid Fuzzy-P+I controller.
With the PI controller, a position error of 0,014 mm
can be achieved only after 60 seconds. With the
Hybrid Fuzzy-P+I the position error is less than 0,5
mm after 0,53 seconds response, 0,05 mm after 0,95
seconds, and 2 µm steady-state position error after
1,015 seconds response. The overshoot was 0,358
mm. When the application of the Hybrid Fuzzy-P+I
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
238

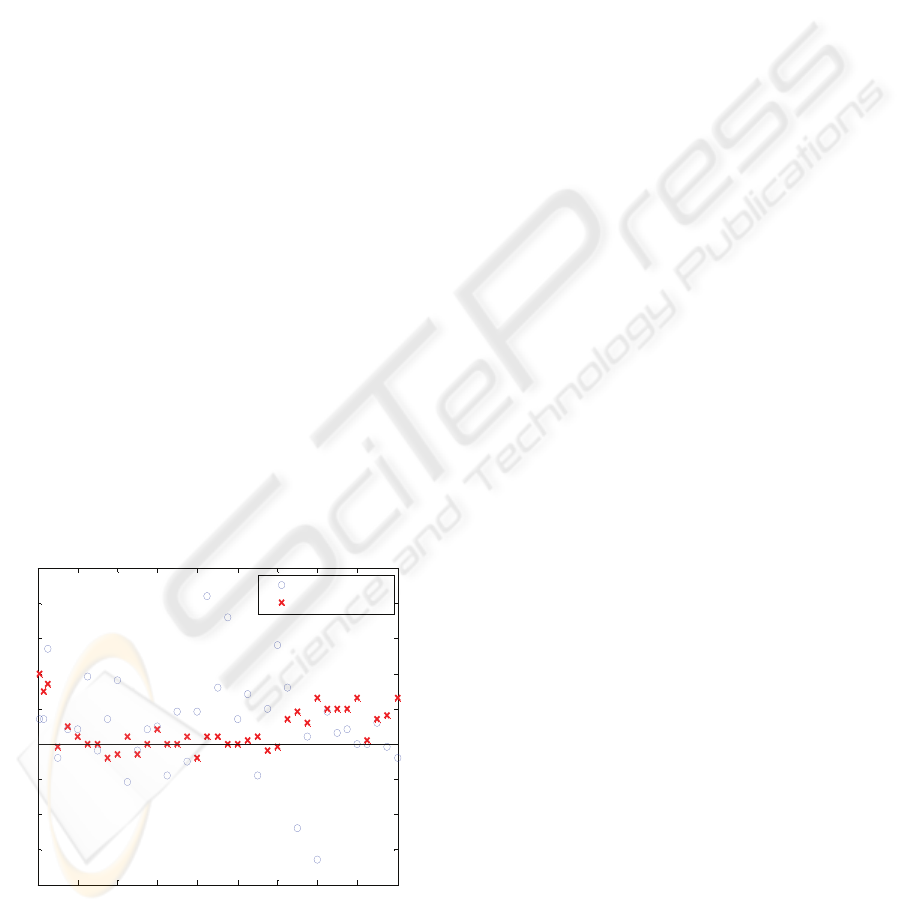
controller makes the mass M to reach its steady-state
position, the position error with the PI controller is
about 8,75 mm.
It was also carry out other experiences to study the
accuracy and repeatability of the overall control
system. Results are shown in Figures 10, which are
relative to the steady-state position error of the PI
and Hybrid Fuzzy-P+I control, respectively, when
were applied step signal references from 0 to
REF_signal mm (multiples of 5 mm, i.e., steps: 0 – 5
mm; 0 – 10 mm; …; 0 – 175 mm; 0 – 180 mm).
The worst steady-state position error of the PI
Control is 0,084 mm, but 3 times reaches below 2
µm of accuracy and 13 times reaches a accuracy
below 10 µm, although its average is 11 µm and
needs a long amount of time to reach these
accuracies. PI control can accurately control the
position of a pneumatic system, however it takes too
long. The sticking and restarting phenomena become
more evident when applied a step signal reference
from 0 to REF_signal mm where 80 mm ≤
REF_signal ≤ 140 mm.
The worst steady-state position error of the Hybrid
Fuzzy-P+I Control is 0,04 mm, but 7 times reaches
below 2 µm of accuracy and 18 times reaches a
accuracy below 5 µm, although its average is 8,6
µm. This controller has achieved a diminution in the
overshoot and in the steady state error compared
with PI and FP controllers, although it suffers some
late correcting the position error. The FP controller
has the shortest rise time and reaches early the
steady-state position. With FLC, with or without the
hybrid solution, the sticking and restarting
phenomena was not observed.
0 20 40 60 80 100 120 140 160 180
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Edge: 0 - REF Signal (mm)
Step Position Error (mm)
PI Control
Fuzzy P+I Control
Figure 10: Steady-state position error of PI and Hybrid
Fuzzy-P+I Control when step references from 0 to
REF_signal mm were applied.
9 CONCLUSIONS
The present paper describes the design and control
of a pneumatic press to perform controlled tracking
of positional reference trajectories. The control
system of the servo pneumatic machine was
implemented with LabVIEW using CompactRIO®
hardware. Conventional PI, proportional Fuzzy and
Hybrid Fuzzy-P+I control strategies were compared
in the position control of a moving mass over 200
mm course. The Hybrid Fuzzy-P+I Controller
provides the best performance for the performed
position control experiments: short rise time, small
overshoot and a steady-state position error that can
reach the encoder resolution, less than 2 µm. It has
particularly advantageous in terms of simplicity of
design and implementation. There is an ongoing
work to implement a high performance force
controller using FLC and the overall pneumatic
system simulation with Matlab/Simulink
®
platform.
REFERENCES
Carneiro, J., Almeida, F., 2006. Modeling Pneumatic
Servovalves using Neural Networks, Proceedings of
the 2006 IEEE Conference on Computer Aided
Control Systems Design, pp. 790-795, Munich,
Germany.
Carneiro, J., 2007. Modelação e Controlo de Actuadores
Pneumáticos Utilizando Redes Neuronais Artificiais,
PhD Thesis in Mechanical Engineering, University of
Porto, Portugal.
Ferreira, J., Sun, P. Grácio, J., 2006. Design and Control
of a Hydraulic Press, Proceedings of the 2006 IEEE
Conference on Computer Aided Control Systems
Design, pp. 814- 819, Munich, Germany.
Liu, H., Lee, J., Li, B., 2007. High Precision Pressure
Control of a Pneumatic Chamber Using a Hybrid
Fuzzy PID Controller, International Journal of
Precision Engineering and Manufacturing, Vol. 8, No.
3, pp. 8-13.
Pai, K., Shih, M., 2003. Nanoaccuracy Position Control of
a Pneumatic Cylinder Driven Table, JSME Int’l
Journal, Series C, Vol. 46, No. 3, pp. 1062-1067.
Passino, K., Yurkovich, S., 1998. Fuzzy Control, Addison
Wesley Longman, Menlo Park, CA.
Santos, M., Talaia, P., Ramos, A., Ferreira, J., Oliveira,
M., 2008. Servo-Pneumatic Machine to Perform and
Monitor Tests on Biomechanical Devices, Controlo
2008: Proceedings of the 8
th
Portuguese International
Conference on Automatic Control, pp. 784 – 789, Vila
Real, Portugal.
Xiang, F., Wikander, J.,2004..Block-oriented Approximate
Feedback Linearization for Control of Pneumatic
Actuator System, Control Engineering Practice 12(4),
pp. 6113-6119.
POSITION CONTROL OF A SERVO-PNEUMATIC SYSTEM - Hybrid Fuzzy P+I Controller of a Servo-Pneumatic
Fatigue Simulator
239