
A FUZZY-CONTROLLED INFLUENCE FUNCTION FOR THE
CULTURAL ALGORITHM WITH EVOLUTIONARY
PROGRAMMING APPLIED TO REAL-VALUED FUNCTION
OPTIMIZATION
Intelligent Control Systems and Optimization
Mário Augusto Torres, Otávio Noura Teixeira and Roberto Limão de Oliveira
Universidade Federal do Pará, Belém, PA, Brazil
Keywords: Cultural Algorithms, Evolutionary Programming, Fuzzy Inference Systems, Real-valued Unconstrained
Function Optimization.
Abstract: In this paper, we propose a fuzzy system to act as a control mechanism for the evolutionary process of
search of a Cultural Algorithm with Evolutionary Programming (CAEP) applied to real-valued function
optimization. The fuzzy system uses population knowledge to adjust the Influence Factor that represents the
intensity of the influence of the Variation operator of the CAEP model, therefore adjusting the search
process. This paper also presents a comparative analysis of the proposed influence function using well-
known benchmarking functions.
1 INTRODUCTION
Fuzzy Systems have been used as control
mechanisms in many applications. From the control
of industrial processes to self adapting air-
conditioners, fuzzy control systems have been
successfully employed due to their capability of
processing uncertain, imprecise knowledge.
Cultural Algorithms (CA) are a class of
evolutionary computational models proposed by
Reynolds, derived from observing the cultural
evolution process in nature (Reynolds, 1994). CA
categorizes the population experience in several
knowledge sources stored in a belief space and
utilizes this knowledge to guide the further evolution
of the population.
The use of fuzzy reasoning as a controller of the
process of acquiring experimental knowledge was
proven to be successful in increasing the
performance of a cultural algorithm with
evolutionary programming (CAEP) system (Chung,
1997).
The fully-fuzzy Cultural Algorithms framework
approach managed to obtain even better results in 12
of the functions that the crisp version of the
framework could not always provide the solution in
the allotted number of generations (Zhu, 1998). The
fully fuzzified approach for the Cultural Algorithm
with Evolutionary Programming (CAEP) system
consisted of a fuzzy acceptance function, a fuzzy
representation of the knowledge contained within
the belief space and a fuzzy influence function (Zhu,
1998).
Still, we believe there is a chance for further
improvement in the fuzzy influence function
proposed in (Zhu, 1998), as a control mechanism for
the search process. The proposal of this paper
utilizes a fuzzy inference system to regulate the
intensity of the EP variation operator based on
imprecise search optimization knowledge, more
specifically cultural influence level knowledge.
2 CULTURAL ALGORITHMS
As stated above, Cultural Algorithms are a class of
evolutionary computational models proposed by
Reynolds, derived from observing the cultural
evolution process in nature (Reynolds, 1994). CA
has three major components: a Population Space, a
Belief Space and a Communication Protocol that
determines how knowledge is exchanged between
240
Augusto Torres M., Noura Teixeira O. and Limão de Oliveira R. (2009).
A FUZZY-CONTROLLED INFLUENCE FUNCTION FOR THE CULTURAL ALGORITHM WITH EVOLUTIONARY PROGRAMMING APPLIED TO
REAL-VALUED FUNCTION OPTIMIZATION - Intelligent Control Systems and Optimization.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,
pages 240-245
DOI: 10.5220/0002210902400245
Copyright
c
SciTePress

the first two components.
The population space can support any
population-based computational model, such as
Genetic Algorithms and Evolutionary Programming
(Reynolds et al., 2005). The belief space is a
knowledge repository, gathered from the behaviour
and individual experiences of the members of the
population space. Saleem (Saleem, 2001) defines
five different knowledge sources, stored and
manipulated within the belief space: Situational
Knowledge, exemplars of successful and
unsuccessful behaviours in the population space;
Normative Knowledge, defining the range of
acceptable or desirable behaviours; Domain
Knowledge, such as knowledge about domain
objects, their properties and relationships; History
Knowledge, that stores temporal patterns of
behaviour; and Topographical Knowledge, that
stores spatial patterns of behaviour of the search
space.
The communication protocol defines how the
members of the population space contribute to the
knowledge gathering within the belief space and
how the knowledge stored in the belief space
influences the individuals in the population space.
To achieve this, two distinct channels are defined:
the Acceptance Function selects the individuals
whose behaviours and experiences will contribute to
update the knowledge in the belief space; and the
Influence Function defines how the knowledge
stored in the belief space influences the operators
that modify the individuals in the population space.
Chung (Chung, 1997), Zhu (Zhu, 1998) and
Rodrigues (Rodrigues, 2007) state that the influence
function works as a self-adaptation mechanism for
the evolutionary process, for it adapts the population
operators according to the gathered knowledge.
The Cultural Algorithm, therefore, is a dual
inheritance system that characterizes evolution in
human culture at both the macro-evolutionary level,
which takes place within the belief space, and at the
micro-evolutionary level, which occurs in the
population space (Reynolds et al., 2005).
Figure 1 depicts the main components of the
Cultural Algorithms framework and their
relationships, adapted from (Saleem, 2000).
Figure 1: Cultural Algorithms Framework (Saleem, 2000).
3 THE CAEP FRAMEWORK
The CAEP (Cultural Algorithm with Evolutionary
Programming), as defined by Chung (Chung, 1997),
is a Cultural Algorithm framework with
Evolutionary Programming as its population
component, and the global knowledge that is learned
by the population expressed as Normative and
Situational knowledge sources. It was successfully
used by Chung in real-valued function optimization.
In the following subsections, the CAEP framework
is briefly explained.
3.1 Evolutionary Programming
Evolutionary Programming (EP) can usually be
described, as in (Fogel, 1996):
1
(1)
where
is the population of solutions in the
iteration t, v() is the variation operator used to
generate new solutions and s() is the selection
operator that determines which candidate solutions
will survive to the next population
1
.
3.2 Belief Space Structure
The formal definition of the belief space in the
CAEP framework is < E, N
[1,…,n]
>, where E is the
set of exemplars of desirable behaviour and
represents the situational knowledge. N
[1,…,n]
is
normative knowledge component, which consists of
a set of interval information for each n parameter.
Each interval in the N set is denoted as < I, U, L >,
where I denotes a closed interval of real numbers x,
represented as:
I = [l,u] = {x | l ≤ x ≤ u} (2)
where l (lower bound) and u (upper bound) are
initialized as the domain values. L
j
represents the
A FUZZY-CONTROLLED INFLUENCE FUNCTION FOR THE CULTURAL ALGORITHM WITH EVOLUTIONARY
PROGRAMMING APPLIED TO REAL-VALUED FUNCTION OPTIMIZATION - Intelligent Control Systems and
Optimization
241

performance score for the lower bound l for the
parameter j and Uj represents the performance score
for the upper bound u for the parameter j (Chung,
1997).
3.3 Acceptance Function
The acceptance function selects the individuals that
will contribute with the formation of the knowledge
in the belief space. There are many possible classes
of acceptance functions. Chung (Chung, 1997)
described a few of these functions.
The acceptance function used in the tests of the
influence function described in this paper is the Top
20%. This function is static in nature and consists in
selecting the top 20% of the individuals in the
population space. It was chosen for its simplicity and
because it provided one of the best results in
Chung’s tests (Chung, 1997).
3.4 Adjusting the Belief Space
In the belief space, the situational knowledge
consists of the current and previous best individuals
found so far. Formally, it is represented as
,
and is adjusted by the following rule:
,
,
(3)
where
is the best individual (solution
parameter vector) found in the population time t
(Chung, 1997).
The normative knowledge component, N, is
updated using the individuals selected by the
acceptance function, which are used to calculate the
current acceptable interval for each of the
parameters of the individuals. In the following, i
represents the individual with the lowest value for
parameter j and k denotes the individual with the
highest value for parameter j. The update rules for
the left boundary and its fitness score for parameter j
are:
.
,
.
,
(4)
,
.
,
(5)
where
denotes the lower limit of the acceptable
interval for parameter j at generation (iteration) t and
represents the performance score for it. The
update rules for the right boundary and its fitness
score for parameter j are:
.
,
.
,
(6)
,
.
,
(7)
where
denotes the upper limit of the
acceptable interval for parameter j at
generation (iteration) t and
represents the
performance score for it.
3.5 Cultured EP Algorithm
The following pseudo-code was proposed by Chung
(Chung, 1997) for a basic “cultured” EP algorithm
and constitutes the skeleton algorithm for the CAEP
framework. Steps (3) and (8), shown in bold
characters, are the procedures added in order to
introduce the cultural aspect in the EP algorithm.
Note that step (4) represents the step where the
influence function is applied for the CAEP
framework and is where the self-adaptation occurs
(Chung, 1997).
(1) Generate an initial population of p candidate
solutions from an uniform distribution within
the given domain for each parameter from 1 to
n;
(2) Assess the performance score for each parent
solution using the objective function;
(3) Initialize the belief space with the given
problem domain and candidate solutions;
(4) Generate p new offspring by applying the
variation operator, v(), as modified by the
influence function. Now, there are 2p solutions
in the population;
(5) Assess the performance score for each offspring
using the given objective function f;
(6) For each individual, select c competitors at
random from the population of 2p size. Next,
conduct pair-wise competitions between the
individual and the competitors and count the
number of wins w
i
for that individual;
(7) Select the p solutions with the greatest number
of wins (w
i
) to be the parents of the next
generation;
(8) Update the belief space by accepting individuals
using the acceptance function described in 3.3.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
242

The belief space is adjusted according to the
rules presented in 3.4.
(9) The process returns to step 4 unless the
available execution time is exhausted or an
acceptable solution has been found.
3.6 Chung’s Influence Functions
The knowledge stored in the belief space can
influence the evolutionary variation operator v in
two ways: (1) determining the size of the mutation
change, called step size, and (2) defining the
direction of the variation, positive or negative
(Chung, 1997). Chung proposed three different
influence functions: The CAEP(Ns), CAEP(Ns+Sd),
and the CAEP(Nsd). Chung showed that the
CAEP(Nsd) had the best results. Thus, this influence
function is described in the following.
3.6.1 CAEP(Nsd)
This version utilizes the normative knowledge to
determine both the size and the direction of the
variation. The basic idea is to perturb small in a
random direction if an individual’s parameter value
is in the acceptable range; otherwise, perturb the
parameter value towards the left or right boundary of
the acceptable range for that parameter in the belief
space. For all individuals i = 1…p and parameters j
= 1…n:
,
,
,
0,1
,
,
,
,
0,1
,
,
,
,
0,1
,
(8)
where
and
represent the lower limit and upper
limit for the parameter j in the generation t,
respectively. β is set to 0.2.
4 THE FUZZY INFERENCE
INFLUENCE FUNCTION (FIS-
NSD)
Many works have been able to achieve some
improvements in real-valued function optimization
by making some aspects of Cultural Algorithms
fuzzy. Chung (Chung, 1997) proposed a fuzzy
acceptance function, based on a fuzzy inference
engine to determine the percentage of accepted
individuals in each generation, taking in
consideration the current generation and the success
ratio of the algorithm as the input of the engine, and
was able to improve the overall performance of the
algorithm in 34 benchmark functions; Zhu (Zhu,
1998) proposed a fully fuzzy cultural algorithm and
was able to improve the results in Chung on 12
benchmark functions.
We propose an influence function based on those
proposed by Chung and Zhu, and incorporating a
fuzzy inference engine to better represent imprecise
search optimization knowledge, more specifically
cultural influence level knowledge.
We used the influence function Nsd proposed by
Chung as the base mechanism to influence the
variation operator. The following is the rule that
defines the proposed influence function. For all
individuals i = 1…p and parameters j = 1…n:
,
,
,
0,1
,
,
,
,
0,1
,
,
,
,
0,1
,
(9)
where ω
i
represents the influence factor that
modifies the intensity in which the variation operator
is applied to the ith individual. This influence factor,
similar to the step adjustment coefficient described
by Zhu (Zhu, 1998), is designed to adjust the search
process in a search optimization knowledge-based
heuristic.
As stated in (Chung, 1997), the age of an
individual is important information because if an
individual is old, that means the it might be trapped
in a local optimum. So, in order to escape, a larger
perturbation might be necessary.
Another important parameter to be considered is
the performance evaluation of an individual. If its
fitness evaluation is considered to be poor, then it
could mean that the individual is farther from
finding the global optimum than the best individuals
in the population, so it might be necessary that the
change we apply in this individual is greater than
that we apply in the best ones. The fitness evaluation
rule of an individual is defined as a real value
between 0 and 1.
The main idea is to regulate the intensity of the
change in the variation operator applied to a parent
individual using a fuzzy inference system. The fuzzy
inference engine receives as input two variables,
corresponding to the age (in number of generations)
of the individual and the fitness evaluation of the
individual, to determine the influence factor ω
i
for
each individual i, from i = 1…p. The fuzzy
inference system is shown in figure 2.
A FUZZY-CONTROLLED INFLUENCE FUNCTION FOR THE CULTURAL ALGORITHM WITH EVOLUTIONARY
PROGRAMMING APPLIED TO REAL-VALUED FUNCTION OPTIMIZATION - Intelligent Control Systems and
Optimization
243
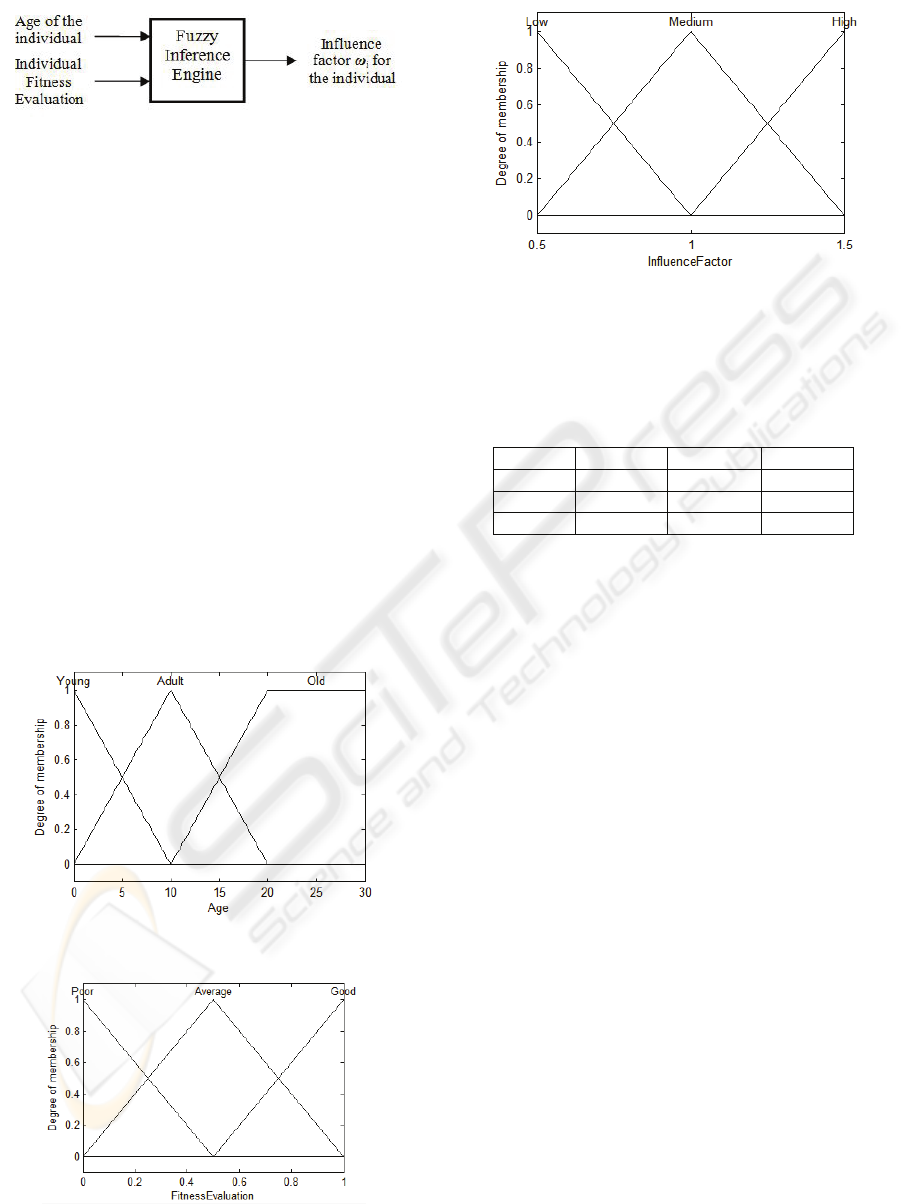
Figure 2: Fuzzy Inference System used to determine ω
i
.
The antecedent membership functions are linear
functions for the fuzzification process and are shown
in the figures 3 and 4. In the fuzzy inference system,
a set of input parameters, representing the age of the
individual and its fitness evaluation, are mapped into
one or more degrees of membership, e.g. Young,
Adult and Old; Poor, Average and Good.
After the fuzzification process, the engine makes
use of the rules shown in figure 4 to infer the degree
of membership of the fuzzy output and provide a
real-valued output ω
i
. The membership function for
the output variable InfluenceFunction is shown in
figure 5.
The basic knowledge represented in the rules
designed in the fuzzy inference system is the
following: if the individual is Old or its fitness
evaluation is Poor, then the influence factor applied
in the variation operator for that individual is High;
if the individual is Young or its fitness evaluation is
Good, then the influence factor concerning this
individual is Low.
Figure 3: Membership Function for the Age parameter.
Figure 4: Membership Function for the Fitness Evaluation
parameter.
Figure 5: Membership Function for the output parameter,
Influence Factor ω
i.
The fuzzy inference rule base used in the fuzzy
inference system is shown in table 1.
Table 1: The Fuzzy Inference Rules used in the FIS.
Poor Average Good
Young
Medium Medium Low
Adult
High Medium Medium
Old
High High Medium
5 TESTS DESCRIPTION
The approach was tested using a set of 14 of the
well-known 25 CEC ‘05 benchmarking functions
(Suganthan et al., 2005), both unimodal (F01 to F05)
and multimodal - basic (F06 to F12) and expanded
(F13 and F14). All functions were used with
dimensionality n = 30.
According to Chung’s results, the best influence
function is the CAEP(Nsd). So, we used this CAEP
configuration to compare with the proposed
CAEP(FIS-Nsd) influence function. Both CAEP
configurations use the top-20% as the acceptance
function, a population size of 60 individuals, iterated
tournament as the selection operator, and were
executed for 25 runs, each run set to 300000
function evaluations (FEs) at maximum, equivalent
to 5000 generations.
6 TESTS RESULTS
The results are shown in tables 2 and 3, depicting the
minimum number of FEs used to solve the function,
the average number of FEs required, the average
fitness value of the best solutions and the success
rate, for each CAEP configuration.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
244

Table 2: Results for the 14 Functions for the CAEP(Nsd)
configuration.
Function MIN FEs AVG FEs
BEST
Fitness
AVG
Fitness
Success
%
F01 12360 12712.8 -450 -450 100
F02 155340 139003.2 -450 -450 100
F03 300000 300000 4.48E5 2.29E6 0
F04 300000 300000 -449.9996 -449.96 0
F05 300000 300000 1553.32 2315.67 0
F06 300000 300000 390.00 410.95 0
F07 300000 300000 4516.28 4516.28 0
F08 300000 300000 -119.14 -119.06 0
F09 300000 300000 -319.05 -260.31 0
F10 300000 300000 -173.88 -167.66 0
F11 300000 300000 95.47 117.13 0
F12 300000 300000 2.75E5 3.82E6 0
F13 300000 300000 -116.52 -115.85 0
F14 300000 300000 -287.01 -286.91 0
Table 3. Results for the 14 Functions for the CAEP(FIS-
Nsd) configuration.
Function MIN FEs AVG FEs
BEST
Fitness
AVG
Fitness
Success
%
F01 10320 10886.4 -450 -450 100
F02 151020 162852 -450 -450 100
F03 300000 300000 3.26E5 4.45E5 0
F04 268268 294892,8 -450 -449.996 36
F05 300000 300000 1964.69 2412.47 0
F06 300000 300000 390.34 397.56 0
F07 300000 300000 4516.28 4516.28 0
F08 300000 300000 -119.29 -119.10 0
F09 300000 300000 212.17 -186.38 0
F10 300000 300000 -173.91 -159.71 0
F11 300000 300000 128.62 129.48 0
F12 300000 300000 1562.40 14900.4 0
F13 300000 300000 -116.78 -116.42 0
F14 300000 300000 -286.68 -286.64 0
7 FINAL REMARKS
We observed that the addition of a fuzzy inference
system to regulate the intensity of the influence
function applied to the individuals alone can
improve the performance of the CAEP(Nsd)
configuration. However, the contribution is only
perceived in unimodal functions, as can be seen in
the results. For improving the performance in
multimodal functions, we envision the addition of
other knowledge sources, such as historical,
topographic and domain knowledge, and fuzzy
influence functions that make use of these
knowledge sources to the CAEP framework as
future work.
REFERENCES
Chung, C., Reynolds, R. G., 1997. Fuzzy Approaches to
Acquiring Experimental Knowledge in Cultural
Algorithms. In Proceedings of the 9th International
Conference on Tools with Artificial Intelligence
(ICTAI), IEEE Computer Society Washington, DC.
Fogel, D. B., 1995. Evolutionary Computation: Toward a
New Philosophy of Machine Intelligence, IEEE Press,
Piscataway, NJ.
Fogel, D. B., Ghozeil, A., 1996. Using Fitness
Distributions to Design More Efficient Evolutionary
Computations. In, Proceedings of IEEE International
Conference on Evolutionary Computation.
Reynolds, R. G., 1994. An Introduction to Cultural
Algorithms. In Proceedings of the Third Annual
Conference on Evolutionary Programming, February
24-26, San Diego, California.
Reynolds, R. G., Peng, B., Whallon, R., 2005. Emergent
Social Structures in Cultural Algorithms. In
Proceedings of the Annual Conference of the North
American Association for Computational Social and
Organizational Science, Notre Dame, Indiana.
Rodrigues, N. M., 2007. Um Algoritmo Cultural para
Problemas de Despacho de Energia Elétrica, Master
Dissertation, Universidade Estadual de Maringá,
Maringá, Paraná, Brazil.
Saleem, S. M., Reynolds, R. G., 2000. Cultural
Algorithms in Dynamic Environments. In Proceedings
of the 2000 Congress on Evolutionary Computation,
La Jolla, CA.
Saleem, S. M., Reynolds, R. G., 2001. Knowledge-Based
Solution to Dynamic Optimization Problems using
Cultural Algorithms. Ph.D. Thesis, Wayne State
University, Detroit, Michigan.
Suganthan, P. N., Hansen, N., Liang, J. J., Deb, K., Chen,
Y. P., Auger, A., Tiwari, S., 2005. Problem
Definitions and Evaluation Criteria for the CEC 2005
Special Session on Real-Parameter Optimization,
Technical report, Nanyang Technological University,
Singapore.
Zhu, S., Reynolds, R. G., 1998. Fuzzy Cultural Algorithms
with Evolutionary Programming for Real-Valued
Function Optimization, Ph.D. Thesis, Wayne State
University, Detroit, MI.
A FUZZY-CONTROLLED INFLUENCE FUNCTION FOR THE CULTURAL ALGORITHM WITH EVOLUTIONARY
PROGRAMMING APPLIED TO REAL-VALUED FUNCTION OPTIMIZATION - Intelligent Control Systems and
Optimization
245
