COMPUTATIONAL ASPECTS FOR RECURSIVE FRISCH SCHEME

SYSTEM IDENTIFICATION

Jens G. Linden, Tomasz Larkowski and Keith J. Burnham

Control Theory and Applications Centre, Coventry University, Priory Street, CV1-5FB Coventry, U.K.

Keywords:

System identiﬁcation, Errors-in-variables, Recursive identiﬁcation.

Abstract:

The implementation of a recursive algorithm for the estimation of parameters of a linear single-input single-

output errors-in-variables system is re-considered. The objective is to reduce the computational complexity

in order to reduce the computation time per recursion, which, in turn, will allow a wider applicability of the

recursive algorithm. The technique of stationary iterative methods for least squares is utilised, in order to

reduce the complexity from cubic to quadratic order with respect to the model parameters to be estimated. A

numerical simulation underpins the theoretically obtained results.

1 INTRODUCTION

In the case of linear time-invariant (LTI) errors-in-

variables (EIV) models not only the output signals

of the system, but also the input signals are as-

sumed to be corrupted by additive measurement noise

(S¨oderstr¨om, 2007b). An EIV model representation

can be advantageous, if the aim is to gain a better

understanding of the underlying process rather than

prediction. One interesting approach for the identi-

ﬁcation of dynamical systems within this framework

is the so-called Frisch scheme (Beghelli et al., 1990;

S¨oderstr¨om, 2007a), which yields estimates of the

model parameters as well as the measurement noise

variances. Recently, recursive Frisch scheme algo-

rithms have been developed in a series of papers by

the authors (Linden et al., 2008b; Linden et al., 2007;

Linden et al., 2008a). This paper considers a fast im-

plementation of the algorithm presented in (Linden

et al., 2008a), which reduces the computational com-

plexity from cubic to quadratic order with respect to

the model parameters to be estimated, hence allowing

a wider range of applicability of the proposed algo-

rithm.

The paper is outlined as follows. The problem of

EIV system identiﬁcation is formulated in Section 2,

where the required notation is also introduced. The

Frisch scheme, being one particular EIV system iden-

tiﬁcation approach is reviewed in Section 3, where

non-recursive and recursive implementations are dis-

cussed. Section 4 develops the novel algorithm which

reduces the computational complexity from cubic to

quadratic order, whilst Section 5 presents numerical

examples. Section 6 contains concluding remarks as

well as direction for further work.

2 PROBLEM STATEMENT

A discrete-time, LTI single-input single-output

(SISO) EIV system is considered, which is deﬁned

A(q

−1

= B(q

−1

, (1)

where i is an integer valued time index and

A(q

−1

) , 1+a

−1

+ ... + a

−n

, (2a)

B(q

−1

) , b

−1

+ ... + b

−n

(2b)

are polynomials in the backward shift operator q

−1

which is deﬁned such that x

−1

= x

i−1

. The noise-

free input u

and output y

are unknown and only

the measurements

= u

+ ˜u

, (3a)

= y

+ ˜y

(3b)

are available, where ˜u

and ˜y

denote the input and

output measurement noise, respectively. Such an EIV

setup is depicted in Figure 1.

The following assumptions are introduced:

A1 The dynamic system (1) is asymptotically stable,

i.e. A(q

−1

) has all zeros inside the unit circle.

136

G. Linden J., Larkowski T. and Burnham K. (2009).

COMPUTATIONAL ASPECTS FOR RECURSIVE FRISCH SCHEME SYSTEM IDENTIFICATION.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 136-141

DOI: 10.5220/0002211401360141

 SciTePress

System

˜y

˜u

Figure 1: Errors-in-variables setup.

A2 All system modes are observable and control-

lable, i.e. A(q

−1

) and B(q

−1

) have no common

factors.

A3 The polynomial degrees n

and n

are known a

priori with n

≤ n

A4 The true input u

is a zero-mean ergodic process

and is persistently exciting of sufﬁciently high or-

der.

A5 The sequences ˜u

and ˜y

are zero-mean, ergodic,

white noises with unknown variances σ

˜u

and σ

˜y

respectively.

A6 The sequences ˜u

and ˜y

are mutually uncorrelated

and uncorrelated with u

and y

, respectively.

A notational convention within this paper is that co-

variance matrices of two column vectors v

and w

are

denoted

, E





, Σ

, E





, (4)

where E[·] denotes the expected value operator. In ad-

dition, vectors consisting of covariance elements are

denoted

, E [v

] (5)

with c

being a scalar. The parameters are elements

within a vector, which is deﬁned by

θ ,







... a

... b



(6a)

θ ,



¯a





1 θ



. (6b)

This allows an alternative formulation of (1)-(3) given

θ = 0, (7a)

, (7b)

where the regression vector is deﬁned by





(8)

, [

−y

i−1

... −y

i−n

i−1

... u

i−n

]





, [−y

]

. (9)

The noise-free regression vectors ϕ

and the vec-

tors containing the noise contributions

are de-

ﬁned in a similar manner. The EIV identiﬁcation

problem is now stated as:

Problem 1. Given an increasing number of k sam-

ples of noisy input-output data {u

,..., u

}, de-

termine an estimate of the augmented parameter vec-

tor

ϑ ,







... a

... b

˜y

˜u



. (10)

Throughoutthis paper, the conventionis made that

estimated quantities are marked by a ˆ whilst time de-

pendent quantities have a sub- or superscript k, e.g.

for a sample covariance matrix corresponding to

3 REVIEW OF THE FRISCH

SCHEME

One possibility to address Problem 1 is the so called

Frisch scheme (Beghelli et al., 1990; S¨oderstr¨om,

2006), which deﬁnes a set of admissible solutions

for the estimates of the input and output measure-

ment noise variances as well as the parameter vec-

tor. In order to single out one particular solution,

different model selection criteria have been proposed

within the literature, leading to different variants of

the Frisch scheme (Hong et al., 2007). The criterion

which is considered here is the Yule-Walker (YW)

model selection criterion described in (Diversi et al.,

2006) and the correspondingFrisch scheme algorithm

is denoted Frisch-YW.

3.1 Non-recursive Frisch Scheme

The estimates of the (non-recursive) Frisch-YW are

characterised by the input measurement noise vari-

ance σ

˜u

, whose estimate, denoted

˜u

, is obtained by

the nonlinear set of equations (Beghelli et al., 1990;

Diversi et al., 2006)

θ =



− Σ

(σ)



−1

ϕy

, (11a)

˜y

= λ

min





, (11b)

˜u

= arg min

˜u

, (11c)

where

(σ) =



˜y

0 σ

˜u



, (12a)

−

− σ

˜u

−1

, (12b)

(θ)k

ζϕ

θ−

ζy

, (12c)

COMPUTATIONAL ASPECTS FOR RECURSIVE FRISCH SCHEME SYSTEM IDENTIFICATION

137

and λ

min

denotes the minimum eigenvalue operator.

The instrument vector ,denoted ζ

, is deﬁned by



k−n

−1

·· · u

k−nb−n



(13)

where n

≥ n

+ n

+ 1 denotes the number of instru-

ments which is user speciﬁed. The quantity r

(θ) de-

notes the nonlinear least squares residual correspond-

ing to a certain θ. Once the σ

˜u

has been estimated,

this value is substituted in (11b) and (11a), in order to

obtain

˜y

and

, respectively. Note that (11a)-(11b)

form the core of the Frisch scheme, whilst (11c) is the

YW model selection criterion with the corresponding

YW cost function, denoted V

. Also note that

de-

pends on

˜u

and

˜y

, where the latter is also a function

˜u

deﬁned by (11b), hence, V

is nonlinear in

˜u

3.2 Recursive Frisch Scheme

Update of θ. The recursive Frisch scheme pre-

sented in (Linden et al., 2008b) is based on the iter-

ative/recursive bias compensating least squares (RB-

CLS) approach (Sagara and Wada, 1977; S¨oderstr¨om,

2007b; Zheng and Feng, 1989). Assuming the noise

covariances have already been obtained, the parame-

ter vector is computed via

+ P

(

)

k−1

, (14)

where

and P

are the least squares (LS) estimate

and corresponding (scaled) error covariance matrix,

respectively. Both quantities are computed via the

well known recursive least squares (RLS) algorithm

(Ljung, 1999)

k−1

+ L



− ϕ

k−1



, (15a)

k−1

1−γ

, (15b)

1− γ

k−1

−

k−1

1−γ

. (15c)

The quantity P

is scaled such that P

= [

]

−1

, whilst

the scaling factor γ

is chosen to be 1 − λ in the case

of exponential forgetting, with λ being the forgetting

factor.

Update of σ

˜y

. For the determination of σ

˜y

, a conju-

gate gradient subspace tracking algorithm (cf. (Feng

and Owen, 1996)) has been utilised in (Linden et al.,

2008b). In order to reduce the computational com-

plexity from cubic to quadratic complexity

, an ap-

The complexity with respect to the number of parame-

ters to be estimated is considered. Note that the conjugate

gradient algorithm in (Linden et al., 2008b) is of cubic order

due to the inverse computation within the Schur comple-

ment (12b) and not due to the subspace tracking algorithm.

proximate algorithm based on the Rayleigh quotient

has been proposed in (Linden et al., 2007). This leads

k−

+ P



k−1

˜y

˜u



k−1

, (16a)

˜y

¯a

k−

¯a

k−

¯a

k−



¯a

k−



, (16b)

where

k−

denotes an intermediate parameter esti-

mate, which makes use of the most recent estimate of

˜u

(which is determined before the update of

˜y

takes

place).

Update of σ

˜u

. For the update of the input measure-

ment noise variance σ

˜u

, a steepest-gradient algorithm

has been proposed in (Linden et al., 2008b). Re-

cently, an alternative approach for the (approximate)

minimisation of (12c) has been suggested in (Lin-

den et al., 2008a). There, the cost function V

modiﬁed by replacing θ in (12c), which is nonlinear

in σ

˜u

due to (11a) and (11b), by the approximation

(

k−1

), which is obtained by making use of lin-

earisations of (11a) and (11b) around the latest esti-

mates

k−1

. These linearisations have been developed

in (S¨oderstr¨om, 2007a) and are given by

≈ L

(

k−1

) ,

k−1



− Σ

(

k−1

)



−1

(17a)



ϕy

−

k−1



˜y

k−1

˜u

k−1



˜y

≈ L

˜y

(

k−1

) ,

k−1

˜y

k−1

¯a

k−1

¯a

k−1



k−1

˜u

−

˜u



(17b)

For a convenient notation, introduce

ι(

k−1

) ,

ϕy

−

k−1

(18a)

k−1

˜y

k−1

¯a

k−1

¯a

k−1

˜u



ˆa

k−1



κ(

k−1

) ,





−

k−1

¯a

k−1

¯a

k−1

ˆa

k−1





, (18b)

(

k−1

) ,

− Σ

(

k−1

). (18c)

Using this notation, the quantity σ

˜y

given by (17b) can

be eliminated in (17a) yielding a linear expression for

θ which only depends on

˜u

(

k−1

) =

k−1

+ Σ

−1

(

k−1

)ι(

k−1

)

+ Σ

−1

(

k−1

)κ(

k−1

)

˜u

. (19)

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

138

Substituting θ in (12c) with L

(

k−1

) allows the ap-

proximate cost function to be deﬁned

lin





(

k−1

)





, (20)

which can be minimised analytically at each time in-

stance k. Differentiating with respect to θ and setting

equal to zero gives

˜u

(

˜u

)



ζϕ



k−1

+ Σ

−1

(

k−1

)ι(

k−1

)



−

ζy



−J

(

˜u

)

ζϕ

−1

(

k−1

)κ(

k−1

)

(21)

where the Jacobian J(

˜u

) is given by

˜u

) =

ζϕ

˜u

, (22)

whilst the total derivative of L

is obtained from (19)

˜u

= Σ

−1

(

k−1

)κ(

k−1

). (23)

The resulting algorithm, which consists of (14)-(16)

and (21) is referred to as recursive Frisch scheme

(RFS) within the subsequent development.

4 FAST RECURSIVE FRISCH

SCHEME ALGORITHM

It is observed that for the computation of the input

measurement noise variance in (21), the matrix Σ

required to be inverted. A matrix inversion is gener-

ally of cubic complexity with respect to its dimension,

which is here equal to n

+ n

, the number of param-

eters to be estimated. Indeed, this matrix inversion is

the bottleneck within the RFS approach described in

Section 3.2, since the remaining operations are only

of quadratic complexity with respect to the model pa-

rameters. Since the intended use for such a recursive

scheme lies in an online computation of the system

parameters, it would certainly be attractive to reduce

the computational burden of the input measurement

noise computation to quadratic order. This would

allow a wider application of the algorithm for cases

where less computational power is available. The de-

velopment of such an algorithm is the topic of this

section.

4.1 First Bottleneck

The ﬁrst bottleneck is due the computation of the in-

verse within the total derivative of L

, which has been

given in Section 3.2 by (23). However, by making use

of stationary iterative methods for solving LS prob-

lems (Bj¨orck, 1996, Chapter 7), Equation (23) can be

re-expressed as

˜u

− Σ

(

k−1

)

˜u

= κ(

k−1

), (24)

where the matrix splitting is given naturally by (18c).

An iterative/recursiveway to compute dL

˜u

could

therefore be given by

′

, P

κ(

k−1

) + Σ

(

k−1

′

, (25)

where L

′

denotes the recursively computed deriva-

tive and P

= [

]

−1

is given by the matrix inversion

lemma of the RLS algorithm, which is already com-

puted for the determination of

4.2 Second Bottleneck

The second bottleneck is due to the matrix inverse

within the computation of (19), therefore, an (approx-

imate) recursive expression for L

(

k−1

) is required,

which is of quadratic complexity only. Firstly, intro-

duce the notation L

(

k−1

) , L

, where the index k

is chosen to reﬂect the fact that L

corresponds to the

linearisation at time instance k (although it depends

on the estimate

k−1

with time index k − 1). Sec-

ondly, assume that all past

have been computed

using the expression (19), which means that

k−1

can

be replaced with L

k−1

in (19). Thirdly, from (18a) and

(18b) it holds

ι(

k−1

) + κ(

k−1

)

˜u

ϕy

−

k−1



ˆa

k−1



k−1

˜y

k−1

¯a

k−1

¯a

k−1

ˆa

k−1

˜u

−

k−1

¯a

k−1

¯a

k−1

ˆa

k−1

˜u



k−1



˜u

, (26)

and by assuming that

˜u

≈

k−1

˜u

˜y

≈

k−1

˜y

and using

k−1

= L

k−1

, one obtains

ι(

k−1

) + κ(

k−1

)

˜u

≈

ϕy

−

k−1



˜y

˜u



k−1

(27)

Finally, by substituting (18c) and (27) into (19), it

holds

− Σ

(

k−1

)

− Σ

(

k−1

)

k−1

ϕy

−

k−1

+ Σ

(

k−1

, (28)

COMPUTATIONAL ASPECTS FOR RECURSIVE FRISCH SCHEME SYSTEM IDENTIFICATION

139

which simpliﬁes to

− Σ

(

k−1

)

= −Σ

(

k−1

ϕy

+ Σ

(

k−1

. (29)

Thus, by using L

k−1

≈ L

, a recursive computation of

the linearised θ-equation (17a) is given by

≈ [

]

−1

ϕy

+ [

]

−1

(

k−1

, (30)

which interestingly is, indeed, the RBCLS algorithm

given in (14) (i.e. simply replace

with L

in (14)).

Since the recursive computation of L

is identical to

the RBCLS computation of

, the latter, more fa-

miliar, notation can be utilised. Substituting the lin-

earised λ

min

-equation (17b), the RBCLS equation be-

comes

+ P



˜y

ˆa

k−1

˜u

k−1



⇔

+ P



k−1



˜u

+ P



ˆa

k−1



(31)

k−1

˜y

k−1

¯a

k−1

¯a

k−1

˜u

−

k−1

¯a

k−1

¯a

k−1

˜u

which simpliﬁes to

= P

ι(

k−1

) + P

κ(

k−1

)

˜u

, (32)

where κ(

k−1

) is deﬁned by (18b) and

ι(

k−1

) ,

ϕy



ˆa

k−1



k−1

˜y

k−1

¯a

k−1

¯a

k−1

˜u

(33)

4.3 Fast Update of

˜u

Using the previous results, a fast implementation for

the update of

˜u

can be realised. With the Jacobian at

time instance k being given by (cf. (22))

ζϕ

′

, (34)

it is therefore possible to compute

˜u

0 = J

ζϕ

−

ζy

(35)

and by substituting

given in (32), the fast update

for

˜u

is ﬁnally given by

˜u

ζy

−

ζϕ

ι(

k−1

)

ζϕ

κ(

k−1

)

. (36)

Note that only matrix vector multiplications are re-

quired for the fast computation of

˜u

, hence the com-

putational effort is reduced towards quadratic com-

plexity. The fast RFS algorithm, which consists of

(14)-(16) and (36) is referred to as FRFS within the

subsequent development.

5 NUMERICAL EXAMPLES

It is of interest to compare the RFS estimates with

those obtained by the FRFS and also to compare the

computation time of both algorithms.

5.1 Estimation of σ

˜u

A LTI SISO system with n

= n

= 2 and given by

θ =



−1.5 0.7 1 0.5



(37a)

σ =



2.1 0.1



(37b)

is simulated for 1000 samples using a zero mean,

white and Gaussian distributed input signal of unity

variance. The RFS and FRFS algorithms are applied

to estimate ϑ using n

= n

+ n

+ 1, whilst λ = 1 is

chosen (i.e. no forgetting). The estimates of σ

˜u

and σ

˜y

are projected into the intervals [0,σ

max

˜u

] and [0,σ

max

˜u

where the maximal admissible values for the input

and output measurement noise variances are chosen

to be σ

max

˜u

= 2σ

˜u

= 0.2 and σ

max

˜y

= 2σ

˜y

= 4.2, respec-

tively. The estimates of σ

˜u

are compared in Figure 2.

Here it is observed that the projection facility (which

200 400 600 800 1000

0.05

0.1

0.15

true

RFS

FRFS

˜u

Figure 2: Estimates of σ

˜u

for using the RFS, and FRFS.

sets

˜u

k−1

˜u

if the estimate is not within the speci-

ﬁed interval) seems to be more often active for the fast

algorithm (see around k = 420). After approximately

500 recursions, however, the FRFS estimate is barely

distinguishable from the RFS, although the FRFS so-

lution seems to be slightly more erratic. Hence, at

least in the example considered here, the FRFS ap-

pears to be able to approximate the estimate of σ

˜u

ob-

tained by the more computationally demanding RFS

algorithm.

5.2 Comparison of Computation Time

Naturally, it is of major interest to compare the com-

putation time per recursion of the FRFS algorithm

with that of the RFS scheme. Therefore, the algo-

rithms are applied to systems with an incrementally

increasing model order m = n

= n

= 1,...,30 and

the computation time per single recursion is recorded

for each identiﬁcation task. The results are presented

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

140

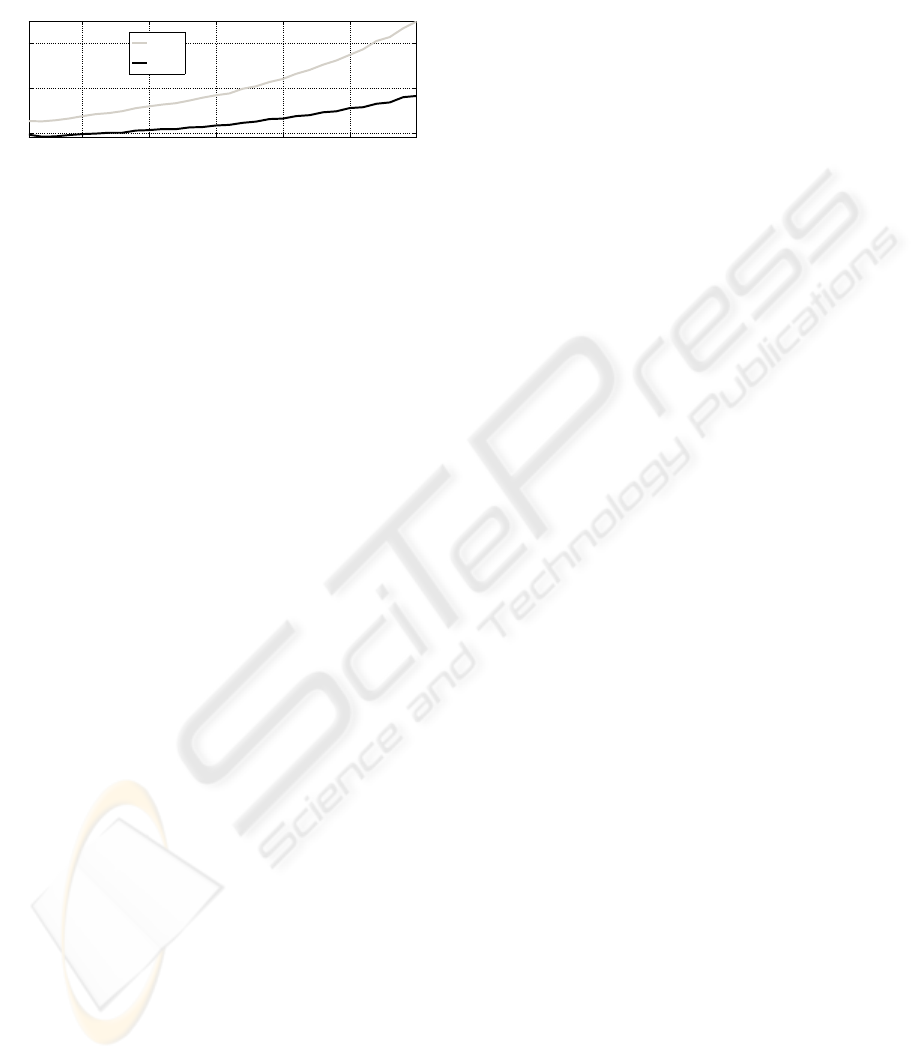
in Figure 3, which clearly shows the relative reduction

of computational complexity for the FRFS approach.

For a model order of m = 30, the RFS requires around

5 10 15 20 25 30

x 10

−3

time[s]

RFS

FRFS

Figure 3: Computation time per single recursion with in-

creasing model order m.

3.5ms, whilst the FRFS requires less than 2.0ms. The

fact that the slope of the curve corresponding to the

FRFS algorithm is lower than that of the RFS ap-

proach illustrates that the computational complexity

is reduced from cubic to quadratic order; this under-

pins the theoretical results obtained in this paper.

6 CONCLUSIONS AND FURTHER

WORK

The Frisch scheme for the identiﬁcation of lin-

ear time-invariant single-input single-output errors-

in-variables systems has been reviewed. The well-

known non-recursive case as well as a recently devel-

oped recursive algorithm has been discussed. Since

the latter is of cubic computational complexity with

respect to the number of parameters to be estimated,

several approximations have been introduced, in or-

der to reduce the complexity from cubic to quadratic

order. This theoretical result is in agreement with the

measured computation time which has been obtained

for a numerical simulation. This simulation has also

shown that the fast algorithm is able to approximate

the solution of the computationally more demanding

algorithm satisfactorily.

Further work could concern the convergenceprop-

erties of the recursive algorithm.

REFERENCES

Beghelli, S., Guidorzi, R. P., and Soverini, U. (1990). The

Frisch scheme in dynamic system identiﬁcation. Au-

tomatica, 26(1):171–176.

Bj¨orck,

A. (1996). Numerical Methods for Least Squares

Problems. SIAM, Philadelphia.

Diversi, R., Guidorzi, R., and Soverini, U. (2006). Yule-

Walker equations in the Frisch scheme solution of

errors-in-variables identiﬁcation problems. In Proc.

17th Int. Symp. on Math. Theory of Networks and Sys-

tems, pages 391–395.

Feng, Y. T. and Owen, D. R. J. (1996). Conjugate gradi-

ent methods for solving the smallest eigenpair of large

symmetric eigenvalue problems. Int. J. for Numerical

Methods in Engineering, 39:2209–2229.

Hong, M., S¨oderstr¨om, T., Soverini, U., and Diversi, R.

(2007). Comparison of three Frisch methods for

errors-in-variables identiﬁcation. Technical Report

2007-021, Uppsala University, Uppsala, Sweden.

Linden, J. G., Larkowski, T., and Burnham, K. J. (2008a).

An improved recursive Frisch scheme identiﬁcation

algorithm. In Proc. 19th Int. Conf. on Systems En-

gineering, pages 65–70, Las Vegas, USA.

Linden, J. G., Vinsonneau, B., and Burnham, K. J. (2007).

Fast algorithms for recursive Frisch scheme system

identiﬁcation. In Proc. CD-ROM 22nd IAR & ACD

Workshop, Grenoble, France.

Linden, J. G., Vinsonneau, B., and Burnham, K. J.

(2008b). Gradient-based approaches for recursive

Frisch scheme identiﬁcation. In Preprints of the 17th

IFAC World Congress, pages 1390–1395, Seoul, Ko-

rea.

Ljung, L. (1999). System Identiﬁcation - Theory for the

user. PTR Prentice Hall Information and System Sci-

ences Series. Prentice Hall, New Jersey, 2nd edition.

Sagara, S. and Wada, K. (1977). On-line modiﬁed least-

squares parameter estimation of linear discrete dy-

namic systems. Int. J. Control, 25(3):329–343.

S¨oderstr¨om, T. (2006). Statistical analysis of the Frisch

scheme for identifying errors-in-variables systems.

Technical report 2006-002, Uppsala University, De-

partment of Information Technology, Uppsala, Swe-

den.

S¨oderstr¨om, T. (2007a). Accuracy analysis of the Frisch

scheme for identifying errors-in-variables systems.

IEEE Trans. Autom. Contr., 52(6):985–997.

S¨oderstr¨om, T. (2007b). Errors-in-variables methods in sys-

tem identiﬁcation. Automatica, 43(6):939–958.

Zheng, W. X. and Feng, C. B. (1989). Unbiased parameter

estimation of linear systems in the presence of input

and output noise. Int. J. of Adaptive Control and Sig-

nal Proc., 3:231–251.

COMPUTATIONAL ASPECTS FOR RECURSIVE FRISCH SCHEME SYSTEM IDENTIFICATION

141