A MHT-BASED ALGORITHM FOR PERFORMANCE ESTIMATION

IN DT-MRI BAYESIAN TRACKING METHODS

L. M. San Jos´e Revuelta

ETSI Telecommunication, University of Valladolid, Campus Miguel Delibes, Valladolid, Spain

Keywords:

DT-MRI. Fuzzy system, Medical image processing, Reliability estimation, Bayesian modelling.

Abstract:

This paper deals with the development of a recursive fuzzy inference system that can be applied to estimate the

error probability of several tracking algorithms used in medical image processing systems. Speciﬁcally, we

are interested in the ﬁber bundles estimation process (ﬁber tracking) in diffusion tensor (DT) ﬁelds acquired

via magnetic resonance imaging (MRI). As tracking algorithm we have considered a variation of the Bayesian

tracking scheme proposed by Friman and Westin. This paper studies the analogies between this tracking

approach and a typical Multiple Hypotheses Tracing (MHT) system, for which fuzzy systems are closely

related. This comparison leads to the development of a SAM (Standard Additive Model) fuzzy system that

on-line estimates the certainty of the estimated ﬁber tracts. Its low computational load as well as its efﬁciency

in very isotropic volumes are its main advantages.

1 INTRODUCTION

The technique of Diffusion Tensor Magnetic Reso-

nance Imaging (DT-MRI) measures the diffusion of

hydrogen atoms within water molecules in 3D space.

Since in cerebral white matter most random motion of

water molecules are restricted by axonal membranes

and myelin sheets, diffusion anisotropy allows de-

piction of directional anisotropy within neural ﬁber

structures (Ehricke, 2006).

There exist many important applications for white

matter tractography: brain surgery, white matter visu-

alization using ﬁber traces and inference of connec-

tivity between different parts of the brain, to name a

few.

The great majority of DTI visualization tech-

niques focuses on the integration of sample points

along ﬁber trajectories and their three-dimensional

representation (Mori, 2002). These streamline-based

approaches are called ﬁber tracking and they usually

make use only of the principal eigenvector of the dif-

fusion ellipsoid as an estimate of the predominant di-

rection of water diffusion in a voxel (Ehricke, 2006).

Nevertheless, and due to some deﬁciencies in these

tracking algorithms and several shortcomings inher-

ent in datasets (noise, partial voluming), they may de-

pict ﬁber tracts which do not exist in reality or miss to

visualize important branching structures. In order to

avoid misinterpretations, the viewer of the visualiza-

tions must be provided with some information on the

uncertainty of a depicted ﬁber and of its presence in a

certain location. This task can be efﬁciently tackled if

a Bayesian approach is used.

In this paper, we have considered a Neural

network-based simpliﬁed implementation of a well-

known Bayesian tracking algorithm (Friman, 2005).

Speciﬁcally, this algorithm has been implemented

with a simpliﬁcation method based on those used in

(San Jos´e, 2005) in the context of a Bayesian detector

for digital multiuser communications.

Our goal is to establish a parallelism between a

standard Bayesian tracking scheme and another pro-

cedure, the Multiple Hypotheses Tracking (MHT)

strategy (Alberola, 1999; Reid, 1979), which is di-

rectly related to fuzzy logic and, to our knowledge,

has not been directly applied to ﬁber estimation. The

thus developed fuzzy system will calculate more reli-

able estimates of the depicted tracts certainty.

2 BAYESIAN TRACKING

ALGORITHM

Bayesian modelling has already been applied to ﬁber

tracking. However, its main drawback is the large

computational load involved. In this paper we pro-

pose to use the Bayesian algorithm of Friman and

445

San José Revuelta L. (2009).

A MHT-BASED ALGORITHM FOR PERFORMANCE ESTIMATION IN DT-MRI BAYESIAN TRACKING METHODS.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 445-448

DOI: 10.5220/0002213204450448

 SciTePress

Westin (Friman, 2005) with the Stochastic Draw-

ing Sampling Selection (SDSS) scheme developed

in (San Jos´e, 2005) for complexity limitation. This

Bayesian algorithm is next described.

The goal of the Bayesian modelling is to ﬁnd a pdf

of the local ﬁber orientation

k−1

, D), where

vectors

and

k−1

contain the path samples up to

time k or k− 1, respectively, and D denotes the mea-

sured diffusion data. If a model that relates the diffu-

sion measurements D with the underlying tissue prop-

erties and architecture is assumed, then it must con-

tain at least one ﬁber direction

and a set of nui-

sance parameters denoted by θ. Thus, applying the

Bayes theorem,

, θ|

k−1

, D) =

p(D|

, θ)p(

k−1

)p(θ)

p(D)

(1)

where we have assumed that the prior distribution can

be factorized p(

, θ|

k−1

) = p(

k−1

)p(θ). The

main problems found are (Friman, 2005): (i) the cal-

culation of p(

k−1

, D) needs to marginalize Eq. (1)

over θ, and (ii) the normalizing factor

p(D) =

,θ

p(D|

, θ)p(

k−1

)p(θ) (2)

is difﬁcult to evaluate due to the high-dimensional in-

tegral and the intractable integrand. Eq. (1) has to be

calculated in every step in the sequential sampling of

the ﬁber paths and, unless an approximation for the

integral in Eq. (2) is found, the cost is prohibitive.

Some attempts have been made to approach this

problem. In (Friman, 2005), a solution based on

drawing samples from a pdf deﬁned on the unit sphere

is proposed. This is accomplished by evaluating the

pdf at a sufﬁciently large number of points evenly

spaced over the unit sphere, effectively approximating

the continuous pdf with a discrete pdf, from which it

is straightforward to draw the random samples. How-

ever, the continuous pdf must be densely enough sam-

pled, speciﬁcally, Friman proposes to use 2,562 pre-

deﬁned points thus involving an important computa-

tional burden. At this point, we propose to use a sam-

pling strategy where those points (hypotheses, in the

Bayesian terminology of (San Jos´e, 2005)) with the

largest probabilities have more chances to be selected.

However, notice that some randomness is introduced

in the selection procedure. This way, those direc-

tions with the highest probability to prolong the cur-

rent ﬁber path will probably be selected. Speciﬁcally,

we have implemented the Stochastic Drawing Sam-

pling Selection (SDSS) algorithm in order to reduce

the number of sampled points in the above-mentioned

unit sphere.

Using the notation found in (Friman, 2005).

3 COMPARISON BETWEEN

BAYESIAN AND MHT

A fuzzy version of Reid’s classical Multiple Hypothe-

ses Tracking (MHT) algorithm (Reid, 1979) was pro-

posed in (Alberola, 1999). This system is based

on the likelihood discrimination and it was applied

to the tracking of natural language text-based mes-

sages. It shows the possibility of handling informa-

tion about any time-varying phenomenon, as long as

the phenomenon can be described by means of a few

keywords, and the phenomenon itself is statistically

causal in the sense that the distribution of future states

is statistically dependent on the past observed states.

It is not difﬁcult to see the following parallelism

that leads to the possibility of a tract probability es-

timation based on text-messages (fuzzy-messages):

(i) the natural-language messages in (Alberola, 1999)

and the noisy DT-MR image constitute, in both cases,

the source of noisy or ambiguous information, (ii) the

tracks used in the MHT algorithm, which are deﬁned

as sequences of associated symbols, can be clearly as-

sociated to the possible sequences of points in the 3D

space, in the tracking context, (iii) the MHT system

associates multiple messages generated along time by

using a speciﬁc stochastic model for the applications’

dynamics. In our case, this model can be the infor-

mation provided by the measured anisotropy, (iv) the

term target denotes some condition that generates ob-

servable phenomena. In our context, these targets are

the sequences of points that deﬁne a tract.

As a consequence, the MHT system can be viewed

as a Bayesian approach for multiple targets track-

ing. Theoretically, this algorithm conserves all the

hypotheses that explain the observation until certain

time, together with an estimation of the probability

of each hypothesis. At the end, the hypothesis with

the highest likelihood is taken as the solution. On

the other hand, the Bayesian tracking algorithm main-

tains a ﬁnite set of hypotheses (section 2) with their

associated probabilities, and a tract is coloured and

visualized based on these data.

4 PROPOSED FUZZY SYSTEM

In this section we propose a recursive SAM (Standard

Additive Model) fuzzy subsystem that allows to mon-

itor the performance of a DT-MRI tracking system.

The SAM model allows to work with linguistic de-

scriptions and ambiguities. This kind of description

allows to fuzzy-quantify the errors in the tractogra-

phy problem. On the other hand, the uncertainty in the

prediction of the future positions found in the MHT of

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

446

(Alberola, 1999), resembles the creation of new ﬁber

tracts based on the previous ones.

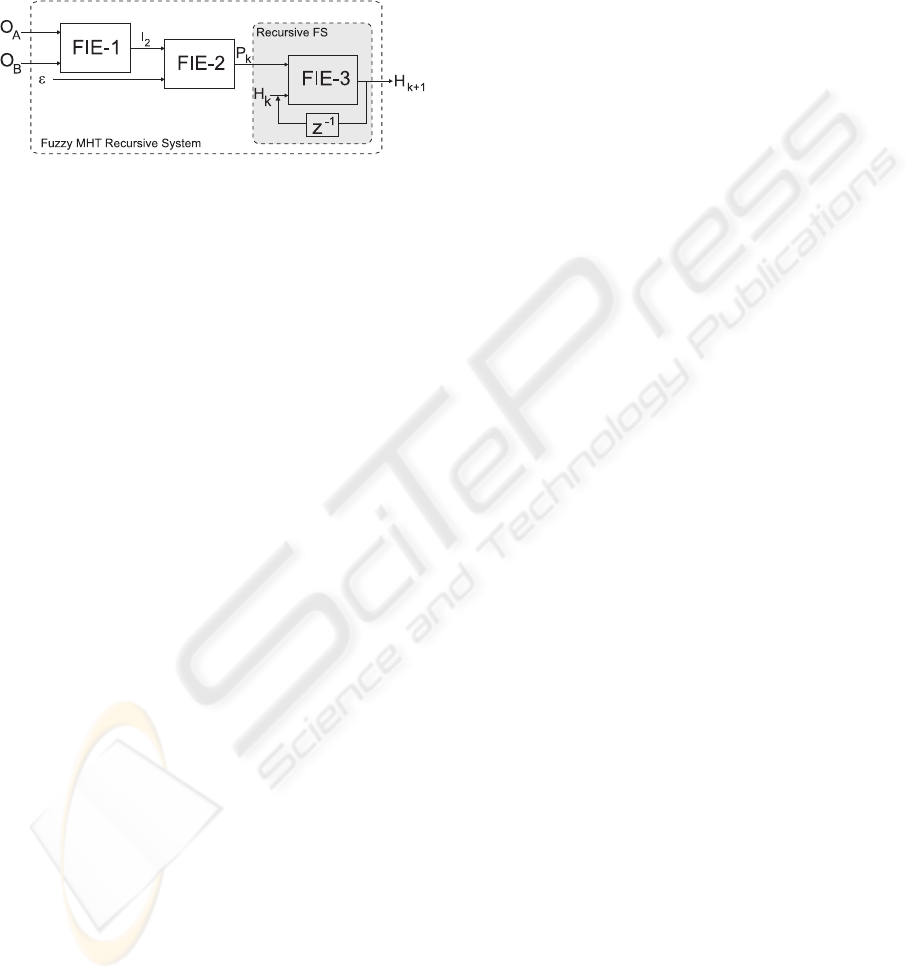
The system here proposed consists in three con-

nected fuzzy inference engines (FIEs) –see Fig. 1. It

is necessary to develop an algorithm where the inputs

to the MHT system have some correlation in time.

Figure 1: Recursive SAM fuzzy system for estimation of

the error probability of the estimated error tracts.

The inputs O

and O

to the FIE-1 are two dif-

ferent tracts (hypotheses) estimated by the algorithm

sharing in common the ﬁrst and the last points (in

practice, both tracts must start and ﬁnish in near vox-

els). These tracts are prolonged on one side with a

new sample every time a new point is considered (at

every iteration of the tracking algorithm), while the

last point of the tracts is lost. This way, compared

tracts have always the same length.

In order to evaluate the similarity between two

tract hypotheses O

and O

, it is necessary to quan-

tify their proximity using a 3D distance. As a con-

sequence, a similarity coefﬁcient that depends on the

distance between these two considered tracts can be

assigned.

In order to implement a fuzzy system, we must es-

tablish a relation between this crisp value (deﬁned in

[0− K]) and the fuzzy sets where a linguistic variable

is deﬁned, i.e.,







K − 1







−→







Very Unlikely

Unlikely

Likely

Very Likely







(3)

This allows to obtain the possible fuzzy values of

(output of the ﬁrst FIE and input to the second).

Next, we relate the prediction error ε used as input

in the FIE-2 with the anisotropy observed in the last

(currently processed) point of the tract. This way, if a

large anisotropy is obtained, the tract would be rather

smooth in the proximity of the current voxel and ε

will take a small value for those hypotheses (future

points to expand the current tract) that involve a small

change in the ﬁber direction. On the other hand, when

the anisotropy is small (isotropic area), parameter ε

would be the same for every direction (hypotheses).

The value of ε must, also, be fuzziﬁed.

This way, FIE-1 estimates the likelihood of two

close tracts while FIE-2 weights this estimate with re-

spect to the prediction error (that is inversely propor-

tional to the anisotropy) and obtains a second likeli-

hood. This value is used to update the global like-

lihood (or global reliability), which is a measure of

the tracking estimation error probability. This third

process is performed by FIE-3. Thus, this third block

updates, with a feedback system, the previous system

knowledge every time a new point is processed.

5 NUMERICAL RESULTS

5.1 Synthetic Images

First, four different synthetic DT-MRI data in a 50×

50 × 50 grid have been generated (three of them –

cross, earth and log– can be seen in Fig. 3 of (San-

Jos´e, 2006) while the fourth one, named star, –the

most complex one– is new. To make the simulated

ﬁeld more realistic, Rician noise was added in the dif-

fusion weighted images which were calculated from

the Stejskal-Tanner equation using the gradient se-

quence in (Westin, 2002) and a b-value of 1000.

The desired noisy synthetic diffusion tensor data

was obtained using an analytic solution to the

Stejskal-Tanner equation. The eigenvectors in the

isotropic areas were λ

= λ

, while in the re-

maining voxels of the image λ

= 7, λ

= 2, λ

= 1.

In our study, the SNR varies from 13 to 29 dB.

The “star” image consists of six orthogonal sine

half-waves, each of them with arbitrary radius. Notice

that this scenario constitutes the most complicated sit-

uation since the diffusion ﬁeld experiments variations

with the three coordinate axes and there exists a cross-

ing region.

The reliability of four approaches for estimat-

ing the tracts certainty is ﬁrst studied. These meth-

ods are: (i) the tracking algorithm described in

(San-Jos´e, 2006), (“ALG”), (ii) the Bayesian algo-

rithm described in section 2 (“BAY”), (iii) ALG with

the fuzzy engine for probability of error estimation

(“ALG+Fuzzy”), and (iv) BAY with the fuzzy pro-

cedure (“BAY+Fuzzy”). Figure 2 shows the mean

probability of wrong estimation (average value in 25

executions) and Table 1 presents the mean variance

of these estimators, for ﬁve different signal qualities

ranging from 13 to 29 dB.

Analyzing the results it can be seen that: (i) the

probability of error increases as the SNR of the orig-

inal image improves; more complex images have

A MHT-BASED ALGORITHM FOR PERFORMANCE ESTIMATION IN DT-MRI BAYESIAN TRACKING

METHODS

447

Figure 2: Mean probability of error for the tracking meth-

ods studied, with and without the fuzzy procedure for esti-

mation of the probability of error. Three synthetic images

were used: earth, log and star.

Table 1: Variance of the tracking error estimation method.

Each cell represents the values for: BAY/ALG/Fuzzy-

estimation.

SNR (dB)

13 21 29

Earth 4.2/3.7/1.6 2.3/1.9/0.7 1.4/0.9/0.2

Log 4.5/4.1/2.0 2.8/2.3/0.9 1.5/0.9/0.3

Star 6.4/5.1/2.8 3.2/2.7/1.5 2.2/1.7/0.7

larger tracking error estimates, (ii) in general, the ac-

curacy of the ALG method is slightly better than the

BAY approach, and (iii) the tracking error of both

methods (BAY and ALG) improves notably when the

fuzzy engine is used for estimation. These ﬁgures are

closer to the real probability of error when a human

expert manually evaluates the tracts obtained.

Table 1 shows how the fuzzy procedure greatly

decreases the variance of the estimator, leading to

more robust and accurate estimations, specially for

low quality images. The values shown in each cell

represent the variance of the different estimation ap-

proaches: BAY, ALG and the fuzzy-based estimation

using the strategy proposed in section 4. The fuzzy

method obtained very similar results when combined

to both BAY and ALG. Thus, only one value is in-

cluded in each cell.

It can be observed that the fuzzy approach gets

estimates with much smaller variances. This esti-

mation procedure is scarcely inﬂuenced by both the

SNR of the image and image complexity (in terms of

anisotropy). This implies that the estimation conver-

gence will not depend on the presence of branching

or crossing areas of the MR ﬁgure –as it would be the

case in real DT-MR images.

5.2 Real Images

Finally, we have applied the proposed tracking algo-

rithm to a real DT-MR image. Speciﬁcally, we have

selected the corpus callosum of the brain.

The variance of the same four estimation meth-

ods has been evaluated. Results are shown in Table

3. Once again the improvement on the estimates reli-

ability can be observed for both BAY and ALG.

Table 2: Variance of different probability of error estimation

methods.

BAY: 8.4 BAY+fuzzy: 3.8

ALG: 7.4 ALG+fuzzy: 3.2

If noisy voxels are present along the paths of in-

terest it is worth noting that the MHT-based fuzzy

method is less sensitive to these variations. The rea-

son is that the MHT performs a kind of smoothing

or data ﬁltering, which decreases the disturbing ef-

fects of the occasionally high noisy samples (this is

addressed using the FIE-3 in Fig. 1).

ACKNOWLEDGEMENTS

The authors acknowledge the Spanish CICYT for re-

search grant TEC2007-67073/TCM.

REFERENCES

Alberola, C., C. G. V. (1999). Tracking with text-based

messages. In IEEE Intell. Systems (14).

Ehricke, H. H., K. U. G. W. (2006). Visualizing mr-dt ﬁelds

by dynamic ﬁber tracking and uncertainty mapping.

In Computers & Graphics (30).

Friman, O., W. C.-F. (2005). Uncertainty in white mat-

ter ﬁber tractography. In Proc. MICCAI 2005, LNCS

3749.

Mori, S., v. Z.-P. C. M. (2002). Fiber tracking: principles

and strategies – a technical review. In Nuclear Mag-

netic Resonance in Biomedicine (15).

Reid, D. B. (1979). An algorithm for tracking nmultiple

targets. In IEEE Tr. Automat. Contr., vol. AC-24.

San Jos´e, L. M. (2005). Hypotheses control-based strategies

for the simpliﬁcation of bayesian multiuser detectors.

In Proc. IEEE XIV Workshop on Machine Learning

for Signal Processing.

San-Jos´e, L. M., M. M. A. C. (2006). A new method for

ﬁber tractography in diffusion tensor magnetic reso-

nance images. In Proc. ICSIP 2006, vol. I.

Westin, C.-F. e. a. (2002). Processing and visualization for

dt-mri. In Med. Image Analysis (6).

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

448