MINIMIZING THE MAKESPAN IN TWO-MACHINE JOB SHOP

SCHEDULING PROBLEMS WITH NO MACHINE IDLE-TIME

Fatma Hermès

Faculté des Sciences Mathématiques, Physiques et Naturelles de Tunis, Département Informatique, Laboratoire LI3

Campus Universitaire, 1060 Tunis, Tunisia

Jacques Carlier, Aziz Moukrim

Université de Technologie de Compiègne, Centre de Recherches de Royallieu

Laboratoire Heudiasyc, UMR CNRS 6599, BP 20529, 60205 Compiègne cedex, France

Khaled Ghédira

Institut Supérieur de Gestion de Tunis, Laboratoire LI3

Université de Tunis, 41 Rue de la Liberté – Bouchoucha, 2000 Bardo, Tunisia

Keywords: Scheduling, Job Shop, Two Machines, No-idle Constraint, Makespan, Optimal Solution.

Abstract: This paper deals with two-machine job shop scheduling problems working under the no-idle constraint, that

is, machines must work continuously without idle intervals. The makespan (C

max

) has to be minimized.

First, we study the problem where each job consists of at most two operations and we show that it can be

solved polynomially using Jackson’s rule (Jackson, 1956). Second, we study the problem where the number

of operations per job can be greater than two and all operations are of unit time and we extend the results of

(Hefetz and Adiri, 1982). Finally, we discuss the possibility of getting feasible solutions and then optimal

solutions in the general case where the number of operations per job can be greater than two and all

operations do not have the same processing time.

1 INTRODUCTION

Frequently, the cost of making machines wait is so

high that a no-idle constraint is imposed on

machines and no intermediate idle time between

operations processed by the same machine is

allowed. For example, if the machine is an oven that

must cook some pieces at a given high temperature

then maintaining the required temperature of the

oven while it is empty may be too costly. However,

studies of problems on this topic have not attracted a

great deal of attention. In the literature, we find

some works, most of which are recent, on the

permutation flow shop ((Adiri and Pohoryles, 1982),

(Baptiste and Lee, 1997), (Kalczynski and

Kamburowski, 2007), (Saadani, Guinet and Moalla,

2001), (Saadani, Guinet and Moalla, 2003)). There

are also some recent works discussing one machine

scheduling problems ((Chrétienne, 2008), (Valente

and Alves, 2005), (Valente, 2006)).

The aim of this paper is to study two-machine

job shop problems where a set I of n jobs, I = {1, ...,

n}, has to be scheduled without intermediate delay

on two machines in order to minimize the maximum

of the completion times of the jobs i.e. the makespan

max

). Each job i, i ∈ I, is composed of n

operations

i,j

, j = 1…n

, and each operation O

i,j

has to be

processed on a fixed machine for p

i,j

time units.

The job shop problem plays an important role in

the scheduling theory because of its practical

applications. Most of job shop problems are NP-hard

and there are only few special cases which can be

solved polynomially. The two-machine job shop

problem with at most two operations per job is

denoted J2|n

≤2|C

max

. It was solved polynomially by

Jackson (Jackson, 1956) who proposed an algorithm

which calculates an optimal schedule in O(n*log(n))

steps using Johnson’s rule (Johnson, 1954). The

two-machine unit-time job shop problem is denoted

Hermès F., Carlier J., Moukrim A. and Ghédira K. (2009).

MINIMIZING THE MAKESPAN IN TWO-MACHINE JOB SHOP SCHEDULING PROBLEMS WITH NO MACHINE IDLE-TIME.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,

pages 89-96

DOI: 10.5220/0002213500890096

 SciTePress

J2|p

i,j

=1|C

max

. It was proved to be polynomial by

(Hefetz and Adiri, 1982) where authors proposed the

longest remaining processing time first algorithm

which schedules operations in a decreasing order of

the remaining processing time of jobs. Lenstra,

Rinnooy Kan and Brucker showed in (Lenstra,

Rinnooy Kan and Brucker, 1977) that problem

J2||C

max

is strongly NP-hard. Later, Brucker showed

in (Brucker, 1994) that the two-machine job shop

problem with a fixed number k of jobs, denoted

J2|n=k|C

max

, can be solved polynomially by reducing

it to a shortest path problem and then he deduced

that it is possible to calculate an optimal schedule for

J2||C

max

for any fixed number of jobs in polynomial

time.

The paper is organized as follows: In section 2,

we define the studied problem and we recall some

backgrounds and basic results relying on the two-

machine job shop problem. In section 3, we study

the two-machine job shop problem where the

number of operations per job is at most equal to two

and machines must work under the no-idle

constraint. This problem is denoted J2|n

≤2,no-

idle|C

max

. We show that it can be solved in

polynomial time using Jackson’s rule (Jackson,

1956). In section 4, we study the two-machine unit-

time job shop problem with no machine idle time,

denoted J2|p

i,j

=1,no-idle|C

max

, and we extend the

results of (Hefetz and Adiri,1982). Finally, in

section 5, we deduce some special cases which are

polynomially solvable.

2 GENERAL POINTS

In this section, we first define the problem subject of

this study and we present some definitions. Next, we

present Johnson’s and Jackson’s algorithms where

Johnson’s algorithm (Johnson, 1954) solves the two-

machine flow shop problem with C

max

criterion

denoted F2||C

max

and Jackson’s algorithm (Jackson,

1956) solves problem J2|n

≤2|C

max

using Johnson’s

rule. Finally we introduce the longest remaining

processing time first algorithm (Hefetz and Adiri,

1982) which solves problem J2|p

=1|C

max

2.1 Problem Formulation and Basic

Definitions

The two-machine job shop problem is a problem

where a set I of n jobs, I = {1, ..., n} have to be

processed in a shop with two machines M

and M

Each job i, i = 1, …, n, consists of a sequence of n

operations O

i,1

, O

i,2

, ..., O

i,ni

which must be

processed in this order. The precedence constraints

are so that O

i,j

precedes O

i,j+1

, j = 1, …, n

– 1. Each

operation O

i,j

must be processed for p

i,j

time units on

machine µ

i,j

∈

, M

The following assumptions are made:

 A machine can process only one operation at a

time.

 An operation cannot be interrupted.

 The time zero is the earliest time an operation

can be started.

 All setup times are included into the job

processing times.

 If operation O

i,j

must be processed on machine

, then operation O

i,j+1

must be processed on

machine M

(µ

i,j

≠ µ

i,j+1

for i = 1,…, n

– 1).

Thus, job i may be characterized by the number

of operations and the machine on which the

first operation must be processed.

 Only no-idle schedules are considered.

Let t

i,j

be the starting time of operation O

i,j

and

let C

i,j

be its completion time. Let C

be the

completion time of job i so that

1...nj

max

i,j

(1)

Let us present the following definitions:

 An initial operation is one without

predecessors: the operation O

i,1

is the initial

operation for job i.

 A terminal operation is one without successors:

the operation

ni,O

is the terminal operation for

job i.

 A ready operation is an operation that has not

yet been scheduled while all its predecessors

have been.

 A no-idle schedule satisfies the no-idle

constraint on each machine. In other words, if

operation O

i,j

is executed immediately before

operation O

i’,j’

on the same machine then we

have:

i,j

= t

i,j

+ p

i,j

= t

i’,j’

(2)

Given a feasible schedule π we have:

max

(π) =

1...nj

1...ni

max

i,j

1...ni

max

(3)

The objective is to find a no-idle schedule so as

to minimize the C

max

. The problem so formulated is

denoted J2|no-idle|C

max

. When the number of

operations per job is at most equal to two, the

problem is denoted J2|n

≤2,no-idle|C

max

and when all

operations have the same processing time which is

considered as the unit-time, the problem is denoted

J2|p

i,j

=1,no-idle|C

max

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

2.2 Jackson’s and Johnson’s

Algorithms

Jackson’s algorithm constructs an optimal schedule

for J2|n

≤2|C

max

problem reducing it to F2||C

max

problem. Below, we first describe Johnson’s

algorithm. Then, we present Jackson’s algorithm.

Finally, we conclude with some results concerning

the presence of idle times on machines.

2.2.1 Johnson’s Algorithm

The two-machine flow shop problem is a problem

where a set I

’

of n

’

jobs, I

’

= {1,2,…,n

’

} must visit

machines in the same order. Each job i consists of

two operations O

i,1

and O

i,2

which must be processed

respectively, first on machine M

then on machine

. Johnson’s algorithm (Johnson, 1954) constructs

an optimal schedule in polynomial time

(O(n*log(n))) for F2||C

max

problem. It applies the

following steps:

i. Divide the set of jobs I

’

, I

’

= {1,2,…,n

’

}, into two

subsets:

a. Let I

’

denote the subset of jobs i, i = 1, …,

’

, which satisfy the condition p

i,1

≤ p

i,2

b. Let I

’

denote the subset of jobs i, i = 1, …,

’

, which satisfy the condition p

i,1

> p

i,2

ii. Schedule on each machine first the jobs of I

’

an increasing order of p

i,1

and then the jobs of I

’

in a decreasing order of p

i,2

2.2.2 Jackson’s Algorithm

Jackson’s algorithm (Jackson, 1956) calculates an

optimal solution for problem J2|n

≤2|C

max

, in

polynomial time (O(n*log(n))) by first reducing it to

F2||C

max

problem and then using Johnson’s rule. It

applies the following steps:

i. Divide the set of jobs I = {1, 2, …, n} into four

subsets:

a. Let I

denote the subset of jobs consisted of

only one operation which must be

processed on machine M

b. Let I

denote the subset of jobs consisted of

only one operation which must be

processed on machine M

c. Let I

1,2

denote the subset of jobs which are

processed first on machine M

then on

machine M

d. Let I

2,1

denote the subset of jobs which are

processed first on machine M

then on

machine M

ii. Calculate an optimal sequence R

1,2

for the flow

shop problem relative to the job set I

1,2

iii. Calculate an optimal sequence R

2,1

for the flow

shop problem relative to the job set I

2,1

iv. On machine M

schedule first I

1,2

according to

1,2

, then all jobs in I

and finally I

2,1

according

to R

2,1

v. On machine M

schedule first I

2,1

according to

2,1

, then all jobs in I

and finally I

1,2

according

to R

1,2

2.2.3 Further Results

Adiri and Pohoryles (Adiri and Pohoryles, 1982)

observe that problems F2|prmu,no-idle|C

max

and

F2|prmu|C

max

are equivalent in the sense that every

F2|prmu|C

max

schedule can be transformed into an

F2|prmu,no-idle|C

max

schedule with maintaining the

same C

max

. Thus, both problems can be solved by

Johnson’s algorithm (Johnson, 1954). Johnson’s

schedule is an active schedule in which machine M

is naturally no-idle since operations are processed

consecutively on it without idle interval. Moreover,

the jobs preceding each idle interval on the second

machine M

can be delayed without increasing the

max

. It is enough to fix the starting time of the last

operation scheduled on M

and to schedule the other

operations so that all operations are scheduled

consecutively without any intermediate delay.

Brucker (Brucker, 1995) observes that in

Jackson’s schedule at least one machine processes

jobs without idle intervals. More specifically, having

the following assumption:

∑

≤

∑

∈∈∈

11,22,1

i,1

i,2

ppp

(4)

then there is no idle time on machine M

. Otherwise,

there is no idle time on machine M

2.3 The Longest Remaining Processing

Time First Algorithm

The longest remaining processing time first

algorithm has been proposed by (Hefetz and Adiri,

1982) to solve J2|p

i,j

=1|C

max

problem. It constructs

an optimal schedule for this problem with applying

the following steps:

i. Give a label α

i,j

to each operation O

i,j

so that:

i,j

= n

– j + 1 i = 1,…,n and j = 1,…,n

(5)

ii. Schedule the highest label operation for the

earliest possible time on the required machine,

with ties broken arbitrarily.

iii. Remove from the problem the scheduled

operation. Stop if all operations are scheduled,

otherwise return to (ii).

The authors noted that the operation with the

highest label in step (ii) must be a ready operation,

MINIMIZING THE MAKESPAN IN TWO-MACHINE JOB SHOP SCHEDULING PROBLEMS WITH NO MACHINE

IDLE-TIME

since, if it is not then there is an unscheduled

predecessor with a higher label, which is a

contradiction.

Let T

, j = 1, 2, be the total processing time

required on machine M

and p

the processing time

of job i. Thus, p

= n

in view of the fact that all

operations have unit duration.

Theorem 1 (Hefetz and Adiri, 1982). The longest

remaining processing time first algorithm constructs

an optimal schedule for J2|p

i,j

=1|C

max

problem. If all

initial operations require the same machine and we

have:

= T

≥ max

(6)

Then, the optimal schedule length is:

max

= T

+ 1 = T

+ 1 (7)

Otherwise, the optimal schedule length is:

max

= max(T

, T

, max

)

(8)

3 RESOLUTION OF THE

PROBLEM

J2|N

≤2,NO-IDLE|C

MAX

The problem we consider in this section is to find an

optimal schedule for J2|n

≤2,no-idle|C

max

problem.

We propose first to study the feasibility of Jackson’s

schedule then, we prove its optimality. We also

deduce some interesting results which concern the

necessity of applying Johnson’s rule in Jackson’s

algorithm.

Proposition 1. The C

max

-value of Jackson’s schedule

is a lower bound for the optimal C

max

of J2|n

≤2,no-

idle|C

max

problem.

Proof. Jackson’s schedule is an active schedule in

which all the operations are scheduled as soon as

possible. On the other hand, to satisfy the no-idle

constraint, some operations must be delayed which

must increase the C

max

-value. So, the optimal C

max

J2|n

≤2,no-idle|C

max

problem must be greater than or

equal to that of J2|n

≤2|C

max

problem.

So, evidently Jackson’s schedule is optimal for

J2|n

≤2,no-idle|C

max

problem if it is no-idle or if it

can be transformed into a no-idle schedule without

increasing the C

max

-value.

Lemma 1. If (4) then there is no-idle time on

machine M

and it is unnecessary for Jackson’s

algorithm to apply Johnson’s rule for the two-

machine flow shop sub-problem relative to I

2,1



0t

’

tTime

1,2

j

1,2



Figure 1: A schedule where there is no-idle time on

machine M

Proof. If (4) holds, then at time t where,

∑

∈∈

11,2

i,1

ppt

(9)

all the operations of I

2,1

which must be processed on

machine M

are ready. Therefore, these operations

can be processed without idle time immediately after

the end of those of I

as presented in figure 1 above.

As a result, the order of processing the

operations of I

2,1

on machine M

and on machine M

does not affect the C

max

-value since all the

operations of I

2,1

which must be processed on

machine M

are naturally ready at time 0. They are

completed at time t

’

, where

i,2

p t'

2,1

≤

∑

∈

(10)

Lemma 2. If

∑

≤

∑

∈∈∈

22,11,2

IiIiIi

i,1

i,2

(11)

then there is no-idle time on machine M

and it is

unnecessary for Jackson’s algorithm to apply

Johnson’s rule for the two-machine flow shop sub-

problem relative to I

1,2

Proof. The proof is similar to that of lemma 1.

Let us note that if

∑

≤

∑

∈∈

1,22,1

IiIi

i,2

i,1

(12)

then (4) holds. Also, if

∑

≤

∑

∈∈

2,11,2

IiIi

i,1

i,2

(13)

then (11) holds.

By summation of (12) and (13), we have:

∑

∈∈

2,11,2

i,2

i,1

(14)

Lemma 3. If any of the following assumptions hold,

namely, (4) and (13), (11) and (12), or (14) then

Jackson’s schedule is no-idle. It is consequently

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

optimal for problem J2|n

≤2,no-idle|C

max

and it is

unnecessary for Jackson’s algorithm to apply

Johnson’s rule neither for the two-machine flow

shop sub-problem relative to I

1,2

nor for the two-

machine flow shop sub-problem relative to I

2,1

Proof. If (4) holds then there is no idle time on

machine M

and it is pointless to apply Johnson’s

rule in Jackson’s algorithm to the sub-problem

relative to I

2,1

(lemma 1).

If (13) holds then there is no-idle time on

machine M

and it is pointless to apply Johnson’s

rule in Jackson’s algorithm to the sub-problem

relative to I

2,1

(lemma 2).

By summation of (4) and (13), Jackson’s

schedule is no-idle. It is consequently optimal for

J2|n

≤2,no-idle|C

max

problem and it is unnecessary

for Jackson’s algorithm to apply Johnson’s rule

neither for the two-machine flow shop sub-problem

relative to I

1,2

nor for the two-machine flow shop

sub-problem relative to I

2,1

In the same way, we deduce the same results if

assumptions (11) and (12) hold or assumption (14)

holds.

Proposition 2. The problem J2|n

≤2,no-idle|C

max

polynomial. It can be solved with Jackson’s

algorithm.

Proof. At least one machine is no-idle (Brucker,

1995). If there is an idle interval on machine M

then

it is between the operations of I

2,1

and in this case

the assumption (4) does not hold. If there is an idle

interval on machine M

then it is between the

operations of I

1,2

and in this case the assumption (11)

does not hold either.

Supposing that machine M

contains an idle

time, then this idle time is between the operations of

1,2

relative to the two-machine flow shop sub-

problem where each job visits first, machine M

then

machine M

. This idle time can be reduced by fixing

the starting time of the last operation scheduled on

machine M

and scheduling the other operations of

1,2

consecutively without any intermediate delay

(Adiri and Pohoryles, 1982).

This action creates an other idle time between

the first operation scheduled of I

1,2

on machine M

and the last operation scheduled of I

on the same

machine.

The last idle time can also be reduced by

delaying all the operations of I

and then the idle

time becomes between the last operation scheduled

of I

2,1

and the first operation scheduled of I

. Since,

there is no idle time on machine M

, then (4) holds.

Let t be the ending date of the last operation of

1,2

scheduled on machine M

and let t

’

be the

starting time of the first operation of I

1,2

scheduled

on machine M

Naturally, we have:

’

≤ t (15)

Because if (15) does not hold, then (4) does not

hold. Consequently, it is possible to shift the

operations of I

2,1

on machine M

to the right so that

there is no-idle time on machine M

Thus, the schedule constructed by Jackson’s

algorithm can be easily transformed into a no-idle

schedule without increasing the C

max

-value. It is

enough to fix the last operation on the machine

which contains idle intervals and shift to the right all

the other operations in order to have no idle

intervals.

As a result, Jackson’s algorithm also constructs

an optimal schedule for he problem J2|n

≤2,no-

idle|C

max

problem.

Proposition 3. The set of optimal solutions of

J2|n

≤2,no-idle|C

max

problem is included in the set of

optimal solutions of J2|n

≤2|C

max

problem.

Proof. Jackson’s schedule can easily be transformed

to a no-idle schedule without increasing the C

max

value. So, both problems have the same C

max

Besides, an optimal solution for J2|n

≤2,no-idle|C

max

problem is also optimal for J2|n

≤2|C

max

problem.

Thus, the set of optimal solutions of J2|n

≤2,no-

idle|C

max

problem is included in the set of optimal

solutions of J2|n

≤2|C

max

problem.

4 RESOLUTION OF THE

PROBLEM J2|p

=1,no-idle|C

max

In this section, we study J2|p

=1,no-idle|C

max

problem.

Proposition 4. The optimal C

max

of J2|p

=1|C

max

problem is a lower bound for the optimal C

max

J2|p

=1,no-idle|C

max

problem; if an optimal schedule

exists.

Proof. The proof is similar to that of proposition 1.

Below, we denote HA the longest remaining

processing time first algorithm. Let S be the

schedule constructed by HA algorithm.

MINIMIZING THE MAKESPAN IN TWO-MACHINE JOB SHOP SCHEDULING PROBLEMS WITH NO MACHINE

IDLE-TIME

Lemma 4. If there is no-idle time in S then the

makespan of S is minimal and the number of idle

times is minimal.

Proof. HA calculates a schedule with minimal

makespan for J2|p

= 1|C

max

problem (theorem 1).

Moreover, if there is no-idle time in S then the

number of idle times is also minimal.

Let us introduce a second criterion to minimize

which is the number of idle times denoted Ā. The

objective is then to minimize first the C

max

then Ā. In

this case, the related problem is denoted

J2|p

=1|Lex(C

max

,Ā).

Evidently, if an optimal schedule for

J2|p

=1|Lex(C

max

,Ā) problem is no-idle then it is

also optimal for J2|p

=1,no-idle|C

max

problem. Also,

if there is no-idle time in S, then S is optimal for

both problems J2|p

=1,no-idle|C

max

and

J2|p

=1|Lex(C

max

,Ā). Furthermore, if it is possible to

built a no-idle schedule S’ from S without increasing

the C

max

then S’ is optimal for both problems

J2|p

=1,no-idle|C

max

and J2|p

=1|Lex(C

max

,Ā).

Let us assume that job h is the job so that

= max

(16)

Figure 2: The schedule resulting from the assumption of

an idle interval on machine M

in interval t and t is even.

Lemma 5. If in S there is an idle time, on some

machine, then

i. the job h is unique, and it is processed

continuously from time

0 to n

, alternating on

the two machines;

ii. the only job processed on the machine

containing this idle time is the job h;

iii. from time t – 1, all the operations processed

on the other machine, except of those of the

job h, must have a label 1.

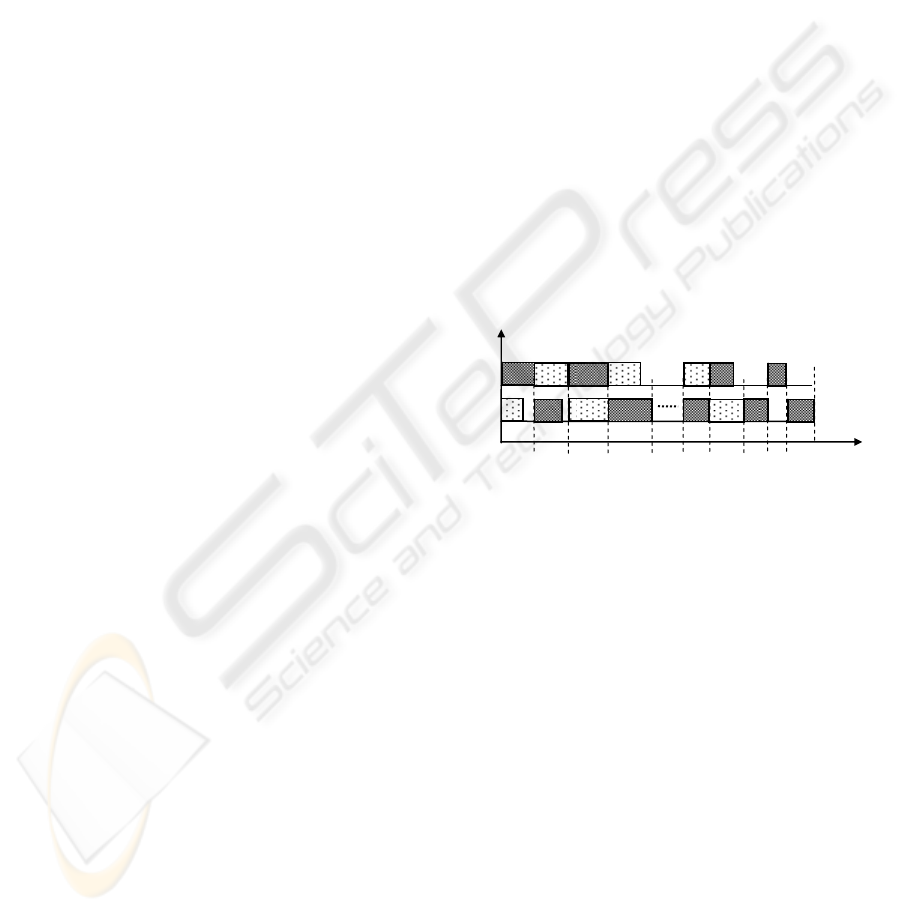
Proof. The time axis is supposed to be split into

intervals of unit times. We suppose that the first idle

interval is the interval t. Let us suppose also that t is

even and that this idle time is on machine M

. Let us

denote i

(resp: j

) the job processed in interval 1 on

machine M

(resp: M

) and so on. So, i

t-1

is the job

processed on machine M

in interval t – 1, and i

the job processed on machine M

in interval t (figure

2). The label of job j

t-1

is 1. Otherwise there doesn’t

exist any idle time in interval t. Consequently, all

jobs processed after t – 1, at the exception of job i

which is the only job which can have a label strictly

larger than 1. Let us set i = i

. We prove that i

t-1

= i.

It is the only job which can have a label strictly

larger than 2. For the same reason i

t-2

= i (the only

job which can have a label strictly larger than 3) and

so on until i

= i. Consequently, i = h. The same

reasoning can be applied when t is odd.

Thus, the job i must be the job h and then the job

h is continuously scheduled from beginning to end

since at each time it have the greatest label. It is

consequently the job h verifying the assumption (16)

and it is unique.

Figure 3: The first operation of job h is processed on

machine M

and machine M

work for the first interval.

Figure 4: The first operation of job h is processed on

machine M

and machine M

is free for the first interval.

Algorithm IT

i. Built S with applying HA algorithm

ii. Built S’ by scheduling the first operation of

job h at time 0 and letting the other machine

idle at time 0 and scheduling the remaining

jobs by applying HA algorithm from time 1.

Theorem 2. One of the two schedules built by

algorithm IT is optimal for both objective functions.

Proof. First, let us note that if there is an idle time in

S then this idle time usually precedes an operation of

job h and it is also preceded with an operation of the

same job h. Indeed, if there is an idle time then the

job h is unique and therefore it is continuously

scheduled from beginning to the end (lemma 5).

Thus, in each interval the job h is processed on one

machine and on the other machine either another job

is processed or there is an idle time. On the other

hand, if the first operation of job h is processed on

t-1

1 2 t-1 t t+1 t

’

-1 t

’

Interval

0 1 2 t-2 t-1 t t+1 t

’

-2 t

’

-1 t

’

Time

t-1

t+1

t-1

1 2 t-1 t t+1 Interval

0 1 2 t-2 t-1 t t+1 Time

t-1

1 2 t-1 t t+1 t

’

-1 t

’

Interval

0 1 2 t-2 t-1 t t+1 t

’

-2 t

’

-1 t

’

Time

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

machine M

then if there is an idle time on machine

which occurs in interval t then t is even and if

there an idle time on machine M

which occurs in

interval t

’

then t

’

is odd. Otherwise, t is odd and t

’

even.

Below, we show in four cases that S or S’ is

optimal for both objectives.

In the first case, we assume that the first

operation of job h is processed on machine M

and

the machine M

works for the first interval of time

(figure 3). In this case, the number of idle times on

machine M

is minimal because the operations

scheduled on machine M

, except of those of the job

h, are used optimally to fill idle intervals created by

the job h. It is the same for machine M

from time 1.

However, if it is possible to make machine begin

working later with one unit of time without

increasing the ending date on this machine and the

max

then we can suppress an idle time. This is done

eventually in S

’

In the second case, we assume that the first

operation of job h is processed on machine M

and

the machine M

works for the first interval of time.

This case is similar to the first one.

In the third case, we assume that the first

operation of job h is processed on machine M

and

the machine M

is free for the first interval of time

(figure 4). In this case, the number of idle times is

minimal in both machines because in each machine

the first operation scheduled is an operation of job h.

In the fourth case, we assume that the first

operation of job h is processed on machine M

and

the machine M

is free for the first interval of time.

This case is similar to the third one.

Thus, S or S’ is optimal for both objectives.

We can resume that S is no-idle if and only if

one of the following cases holds:

Case 1:

max

≤ min(T

, T

)

(18)

Case 2:

max

= min(T

, T

) + 1 (19)

and the last operation of the job h is scheduled on

the machine which determines the schedule length.

Case 3:

max

= min(T

, T

) + 2 (20)

and all jobs begin in the same machine and the last

operation of the job h is scheduled on the machine

which determines the schedule length.

Finally, we note that S’ is no-idle if S is no-idle

or S contains only one idle time.

5 RESOLUTION OF THE

PROBLEM J2|n=k, no-idle|C

max

In this section, we discuss J2|n=k,no-idle|C

max

problem.

Proposition 5. The optimal C

max

of J2|n=k|C

max

problem is a lower bound for the optimal C

max

J2|n=k,no-idle|C

max

problem; if an optimal schedule

exists.

Proof. The proof is similar to that of proposition 1.

So, the optimal schedule for J2|n=k|C

max

problem

is optimal for J2|n=k,no-idle|C

max

problem if it is no-

idle or if it can be transformed into no-idle schedule

without increasing the C

max

-value.

Obviously, if n = 1 and n

> 2 then it is not

possible to construct a no-idle schedule. There are

exactly n

– 2 idle intervals.

Let us consider the problem where the number of

jobs is equal to two. This problem is denoted

J2|n=2,no-idle|C

max

Figure 5: Schedule format with two jobs where n

> n

Let us give the following cases:

Case 1: n

= n

, μ

1,1

≠ μ

2,1

and p

1,j

= p

2,j

for

j = 2… n

– 1

Case 2: n

= n

, μ

1,1

= μ

2,1

and p

1,j+1

= p

2,j

for

j = 1… n

– 1

Case 3: n

= n

, μ

1,1

= μ

2,1

and p

1,j

= p

2,j+1

for

j = 1… n

– 1

Case 4: n

= n

+1, μ

1,1

≠ μ

2,1

and p

1,j

= p

2,j

for

j = 2… n

Case 5: n

= n

+ 1 and μ

1,1

= μ

2,1

and p

1,j+1

= p

2,j

for j = 1…n

– 1

Case 6: n

= n

+ 1, μ

1,1

≠ μ

2,1

and p

1,j

= p

2,j

for

j = 2…n

Case 7: n

= n

+ 1, μ

1, 1

= μ

2,1

and p

1,j

= p

2,j+1

for

j = 1…n

– 1

Case 8: n

= n

+ 2, μ

1,1

= μ

2, 1

, and p

1,j+1

= p

2,j

for j = 1…n

Case 9: n

= n

+ 2, μ

1,1

= μ

2, 1

, and p

1,j

= p

2,j+1

for j = 1…n

t T=

1 1

2 2

MINIMIZING THE MAKESPAN IN TWO-MACHINE JOB SHOP SCHEDULING PROBLEMS WITH NO MACHINE

IDLE-TIME

Proposition 6. If any of the previous cases holds

then the no-idle schedule is unique; it is

consequently the optimal solution for J2|n=2,no-

idle|C

max

problem. Otherwise, it is impossible to get

a no-idle schedule.

Proof. A feasible schedule for J2|n=2|C

max

problem

takes the format presented in figure 5 above.

Clearly, having this format, it is not possible to

transform any schedule to a no-idle schedule. There

are at most max(n

, n

) – 2 idle intervals.

However, we deduce that if any of the previous

cases holds then the no-idle schedule is unique. It is

consequently the optimal solution for J2|n=2,no-

idle|C

max

problem. Otherwise, it is impossible to get

a no-idle schedule.

6 CONCLUSIONS

In this paper, we have studied the impact of adding

the no-idle constraint to the problem of minimizing

the makespan in a two-machine job shop. We have

studied separately the case where the number of

operations per job isn’t greater than two and the case

where all operations are of unit time. In the first case

we have showed that there exists usually an optimal

schedule which we can calculate using Jackson’s

rule and then fixing the last operation scheduled on

the machine which contains an idle time and then

scheduling the other operations consecutively

without idle times. However, in the second case, we

showed that it is not usually possible to build a

feasible no-idle schedule. Then, we have proposed

the IT algorithm which minimizes first the C

max

then

the number of idle times (Ā). We have shown that it

is impossible to build a schedule which contains a

number of idle times smaller than that of the

schedule obtained by applying IT algorithm.

Consequently, if this schedule is no-idle then it is

also optimal for the corresponding problem with

adding the no-idle constraint. Moreover, in the

general case, where the number of operations per job

can be greater than two and all operations do not

have the same processing time, we have shown that

where the number of jobs is equal to two there are

only few cases numbered from 1 to 9 which are

efficiently solvable and where the set of feasible no-

idle schedules contains a unique schedule. In

conclusion, we deduce that it is not usually possible

to construct a feasible no-idle schedule for the two-

machine job shop problem and that in the majority

of cases, this set is empty.

REFERENCES

Adiri, I., Pohoryles, D., 1982. Flow-shop/no-idle or no-

wait scheduling to minimise the sum of completion

times.

Naval Research Logistics Quarterly, Vol. 29,

pp. 495-504.

Baptiste, P., Lee, K.H., 1997. A branch and bound

algorithm for the F|no-idle|C

max

. Proceedings of the

International Conference on Industrial Engineering

and Production Management (IEPM’1997)

, Lyon, vol.

1, pp. 429-438.

Brucker, P., 1994. A polynomial algorithm for the two

machine job-shop scheduling problem with fixed

number of jobs.

Operations Research Spektrum, Vol.

16, pp. 5-7.

Brucker, P., 1995. Scheduling Algorithms,

Springer,

ISBN: 3-540-60087-6.

Chrétienne, P., 2008. On single-machine scheduling

without intermediate delays.

Discrete Applied

Mathematics, 156, p. 2543-2550.

Garey, M.R.D., Johnson, D.S., Sethi, R., 1976. The

complexity of flowshop and jobshop scheduling.

Mathematics of Operations Research, Vol. 1, pp. 117-129.

Hefetz, N. , Adiri, I., 1982. An Efficient Optimal

Algorithm for the Two-Machines Unit-Time Jobshop

Schedule-Length Problem.

Mathematics of Operations

Research, Vol. 7, No. 3., pp. 354-360.

Jackson, J.R., 1956. An extension of Johnson’s results on

job lot scheduling.

Naval Research Logistic Quarterly,

Vol. 3, pp. 201-203.

Johnson, S.M., 1954. Optimal two- and three-stage

production schedules with setup times included,

Naval

Research Logistics Quarterly, Vol. 1, pp. 61-68.

Kalczynski, P. J., Kamburowski, J., 2007. On no-wait and

no-idle flow shops with makespan criterion.

European

Journal of Operational Research, Vol. 178, pp. 677–685.

Lenstra, J. K., Rinnooy Kan, A.H.G., Brucker, P., 1977.

Complexity machine scheduling problems.

Annals of

Discrete Mathematics

, Vol. 1, pp. 343-362.

Saadani, H., Guinet, A., Moalla, M., 2001. A travelling

salesman approach to solve the

F|no-idle|C

max

problem.

Proceedings of the International Conference on

Industrial Engineering and Production Management

(IEPM’ 2001)

, Quebec, vol. 2, 880-888.

Saadani, H., Guinet, A., Moalla, M., 2003. Three stage no-

idle flow-shops.

Computers and Industrial

Engineering

, 44, 425-434.

Valente, J. M. S., Alves, R. A. F. S., 2005. Improved

Heuristics for the Early/Tardy scheduling problem with

no idle time.

Computers & Operations Research, 32: p.

557-569.

Valente, J. M. S., 2006. Heuristics for the single machine

scheduling problem with early and quadratic tardy

penalities. Working paper 234, Faculdade de Economia

do Porto, Portugal, December.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics