
Evolving Gradient a New Approach to Perform Neural
Network Training
C
´
esar Dalto
´
e Berci and Celso Pascoli Bottura
Faculdade de Engenharia El
´
etrica e Computac¸
˜
ao, Universidade Estadual de Campinas
Av. Albert Einstein 400, Campinas, Brazil
Abstract. The use of genetic algorithms in ANNs training is not a new subject,
several works have already accomplished good results, however not competitive
with procedural methods for problems where the gradient of the error is well
defined. The present document proposes an alternative for ANNs training using
GA(Genetic Algorithms) to evolve the training process itself and not to evolve
directly the network parameters. This way we get quite superior results and obtain
a method competitive with these, usually used to training ANNs.
1 Introduction
Artificial Neural Networks is a computational paradigm inspired in the operation of the
biological brain, especially in the human brain, and seeks to explore certain properties
present in the human neural processing, that are very attractive from the computational
view point. Among the principal characteristics of the biological information process-
ing, the following can be mentioned [9]:
– Robustness and fault Tolerance. The human brain possesses a great number of neu-
rons and even losing thousands of them, the brain may continues in operation with-
out losing its capacities.
– Flexibility. There is no need to reprogram the system when exposed to new un-
known situations. In these cases the brain has the capacity to assimilate the new
scenery and to adapt to it.
– Possibility of working with fuzzy, probabilistic, noisy and inconsistent information.
The neural computation has the intrinsic ability to work with uncertainties, which
conventionally requires a high sophistication level to be treated by more conven-
tional computational paradigms.
– Parallelism. Neural computers, as the human brain, are parallel in their essence,
what turns them highly efficient for treating certain problems.
Another computational method, also bio-inspired, are the genetic algorithms, based
on Charles Darwin’s work, more precisely in his book The Origin of Species [6] where
the author idealizes the natural selection mechanism. The philosopher Daniel Dennett
great defender of Darwin’s theories, presents in his book: Darwin’s Dangerous Idea:
Evolution and the Meanings of Life [7], a engineering vision of the evolution theory,
being this one of the most influential works on the subject today.
Berci C. and Bottura C. (2009).
Evolving Gradient a New Approach to Perform Neural Network Training.
In Proceedings of the 5th International Workshop on Artificial Neural Networks and Intelligent Information Processing, pages 3-12
DOI: 10.5220/0002214000030012
Copyright
c
SciTePress

Genetic algorithms are computational devices, based on biological evolutionary
processes, designed to find optimum and sub-optimum solutions for computational
problems. An usual application case of this tool, is in continuous function optimization,
where the genetic algorithms can be viewed as a multi objective global optimization
tool, that finds the function extreme points through a blind search mechanism, based on
the evolution of previous solutions.
The optimization problem extends to several areas of the exact sciences, including
the optimization of the ANNs parameters vector
1
, also known as ANNs learning or
training, because this process trains the network to recognize a certain pattern relating
its inputs to its outputs.
That training usually occur through iterative optimization methods, based on the
gradient descent of the ANN error surface, which is calculated through the backpropa-
gation algorithm [14],[15]. Among the more efficient methods known today for ANNs
training can be mentioned, the quasi-Newton method: BFGS [1] and the conjugated
directions method: Scaled Conjugate Gradient [11],[12].
An alternative way to find desired the ANNs parameters vector, is the use of meta-
heuristic methods, as the genetic algorithms. Several researchers are using those algo-
rithms directly in the optimization of the error surface with respect with parameters
vector[16],[13],[17]. There are others works using genetic algorithms not only to opti-
mize the network with respect to its parameters vector, but also other parameters as its
topology [4],[8].
In spite of genetic algorithms represent a tool of great computational power to train
ANNs, it does not have the same efficiency as procedural optimization methods, that
uses more information about the problem (first and/or second order information), and
usually produce better results.
The present document, introduces a new optimization concept for using genetic al-
gorithms for ANN training, where an sub-optimum gradient is used, and steps are taken
in the direction of this gradient. This proposal makes use of the full exploratory capacity
of the genetic algorithms, united with the efficiency of gradient descent methods, reach-
ing very superior results to those obtained by both techniques when applied separately.
2 Neural Networks Training
Artificial Neural Networks are devices with the universal approach capacity, and are in
general applied to assimilate mappings, using for this a chain of interconnected artificial
neurons, that interact each other in a similar way of the natural neural information
processing.
This devices have also a formal mathematical representation, given by a mapping
with inputs and outputs, which are expressed as a nonlinear function of its input, as
described following:
y = F(x, θ) (1)
1
In this work, is considered the ANN parameters vector, a vector ω ∈ R
N
containing the values
of all network weighs and bias
4

where θ is the ANN parameters vector.
A priori it is not possible to determine an appropriated parameters vector θ such
that the network expresses correctly any desired mapping y = H(x), therefore it is
necessary to train the ANN to find a parameters vector, which produces the desired
behavior.
In general, is not possible to find the parameters vector analytically, than, the net-
work learning process is iterative, and seeks to increase the network adaptation to the
target mapping at each iteration (also known as epoc). To make possible this task, an
error is defined for the network output, that expresses the difference between the cur-
rent behavior and the desired one. A possible definition for the network error, which is
adopted in this work, can be the following:
e =
X
i
(H
i
(x) − F
i
(x, θ))
2
!
/n
o
(2)
where H is the target mapping that one wants to assimilate by the ANN, and n
o
is the
number of neurons on the output layer.
This error is a functional and creates a smooth surface in the space R
N
, where N is
the dimension of the vector θ, therefore the process of ANN training can be seen as the
minimization of the error surface with respect to its parameter: θ.
3 The Evolving Gradient
There are some works that try to optimize the weight vector of the ANN using a genetic
algorithm. This process is in general more onerous from the computational cost
2
view-
point, and shows poor results when compared to conventional optimization methods
based on gradient descent.
The present document, presents an alternative solution inspired in the work of Chalmers
The Evolution of Learning: An Experiment in Genetic Connectionism[5], that applied
evolutionary processes to evolve the learning process itself.
In the EG: Evolutionary Gradient method, the genetic algorithms are not used to
optimize the weights vector, but to optimize the process by evolving the gradient vector.
3.1 Codification
The genetic algorithm implemented in the proposed EG algorithm, uses a population of
n
p
individuals, with a real codification, described as follows:
– Chromosome: Vectors containing real values belonging to the space R
N
– Fitness: exp (−αe(x, θ − p)) where α it is a parameter to be adjusted, and p is a
chromosome.
– Selection: Roulette and Elitist.
2
here computational cost of a procedure is understood, the number of sum and multiplication
operations necessary for accomplish this
5

– Reproduction: Matrix method [2] designed with based on the subspaces generated
by parents chromosomes.
– Mutation: A Gaussian mutation modifying all components of the chromosome by
adding a random noise.
In this code n
rep
pairs are chosen for reproduction through a roulette mechanism,
where n
rep
∈ [1, n
p
] is a random number. The remaining of the population n
p
− n
rep
is chosen with an elitist selection procedure, to avoid loosing of the best solution and
also to preserve the population diversity.
3.2 The EG Algorithm
This algorithm is based on gradient descent algorithm, where steps are taken in the
direction of the gradient vector, however, here steps are taken in the direction of a sub-
optimum gradient evolved by the genetic algorithm previously discussed.
To each iteration of the algorithm, an initial gradient vector is calculated using the
Backpropagation method, or simple taken equals to the origin. Later a new population
is created, and this gradient is introduced in the population, that will be evolved by
the genetic algorithm during n
i
generations, and then, an unit step is taken in this new
evolved direction.
The use of the initial gradient seeks to accelerate the convergence of the evolution-
ary process, giving to him a reference point. It is also possible the method execution
calculation of the initial gradient, as can be seen in [3]. This procedure is useful when it
is not possible to accomplish the ANN retro-propagation phase, impeding the gradient
vector construction, what enlarge the application range of the EG.
The EG algorithm for ANNs training is describe following.
Algorithm 1: Evolving Gradient.
Determine: n
p
, n
i
, n
max
;
Initialize: θ;
for i=1 to n
max
do
Calculate g
0
by the retro-propagation of the error, or just set g
0
= 0;
Evolve the gradient: g = AG(n
p
, n
i
, g
0
) ;
Unit step: θ
i+1
= θ
i
− grad
end
where AG represents a genetic algorithm.
The algorithm 1, is the result a exhaustive study of the training process, and the
functional analysis of the relations between the quantities of interest, taking into account
the dimensionality of the involved spaces and the characteristics a priori known about
the problem.
These studies converged to a method where the genetic algorithm is applied in a
space of same dimension of the parameters vector. However, this choice brings a great
advantage with respect to the cost function to be optimized.
In the application of a blind search method, as in case, the efficiency of the opti-
mization process may be considerably increased if the method is initialized near the
6

neighborhood of a local optimum point, which represents a good solution to the prob-
lem. However, this points are not known a priori, nor their neighborhoods.
The same happens in the ANNs training, the error surface are not complete known,
so nothing can be done to increase the training algorithm efficiency. Moreover, it is
known that a sufficient small step in a descent direction is ways a minimizing step.
Therefore, we conclude that a R
N
vector, representing a descent direction, will be cer-
tainly found in a neighborhood of the origin.
This information is the main goal of the EG, given to blind search method what it
needs, a good initial condition. This approach gives to genetic algorithm a considerable
efficiency increase, so the algorithm EG here proposed, presents a significantly higher
convergence rate when compared with others meta-heuristic methods in the same con-
text.
Another important feature of the EG, is the intrinsic parallelism of the algorithm. Its
implementation in a sequential machine, as a digital computer, will generates a process
computationally very onerous, however, in a completely parallel machine, still hypo-
thetical, is obtained a very faster and efficient process.
4 Examples and Comparisons
With the intention of determining the relative efficiency of the EG compared with others
founded in the literature, some ANN application examples are used, and the efficiency
of the learning process is evaluated when the network is trained by different methods.
In this document will be considered, as comparison bases, two quasi-Newton meth-
ods, two conjugated directions methods and one simple gradient descent method, all
described as follows:
– GRAD: Optimium Gradient [10]: Gradient descent method with super-linear con-
vergence, the fastest among methods with linear convergence rate.
– DFP: Davidson Fletcher Powell [10]: quasi-Newton Method with quadratic con-
vergence.
– BFGS:Broyden Fletcher Goldfarb Shanno [1]: quasi-Newton Method with quadratic
convergence, and with smaller sensibility to the bad numerical conditioning than
the DFP method.
– FR: Fletcher Reeves [1]: Conjugated directions method, with N-steps quadratic
convergence.
– SCG: Scaled Conjugated Gradient[12]: Conjugated directions method that do not
use unidimensional searches. It possesses N-steps quadratic convergence, and it is
the fastest among these methods from the computational cost viewpoint.
The process of unidimensional search used in the algorithms GRAD, DFP, BFGS
and FR is the golden section method, applied by 30 iterations on the initial interval.
4.1 Motor Currents
In theory, the current of a three-phase induction motor can be easily calculated on the
basis of motor voltage and power, as shown in equation (3).
7
I =
P
√
3V η
(3)
where P and V represent the motor power and tension respectively. The variable
η takes into account the power factor and efficiency of the motor, that are based on
construction factors, the mechanical load and the rotation of the motor. Thus, it is clear
difficult to specify the variable η and so, the motor current.
The problem in question uses a neural estimator for the current calculation, based
on motor power, voltage and rotation, through a MLP network containing 3 neurons in
its sensorial layer, and with 1 neuron in its output layer.
The set used in the training consist on 300 samples obtained from manufacturers
catalogs, including motors that meet the following values ranges:
– Power: 0.1 a 330 KW.
– Rotation: 600,900,1200,1800 e 3600 rpm.
– Tension: 220, 380 e 440 V.
– Current: 0.3 a 580 A.
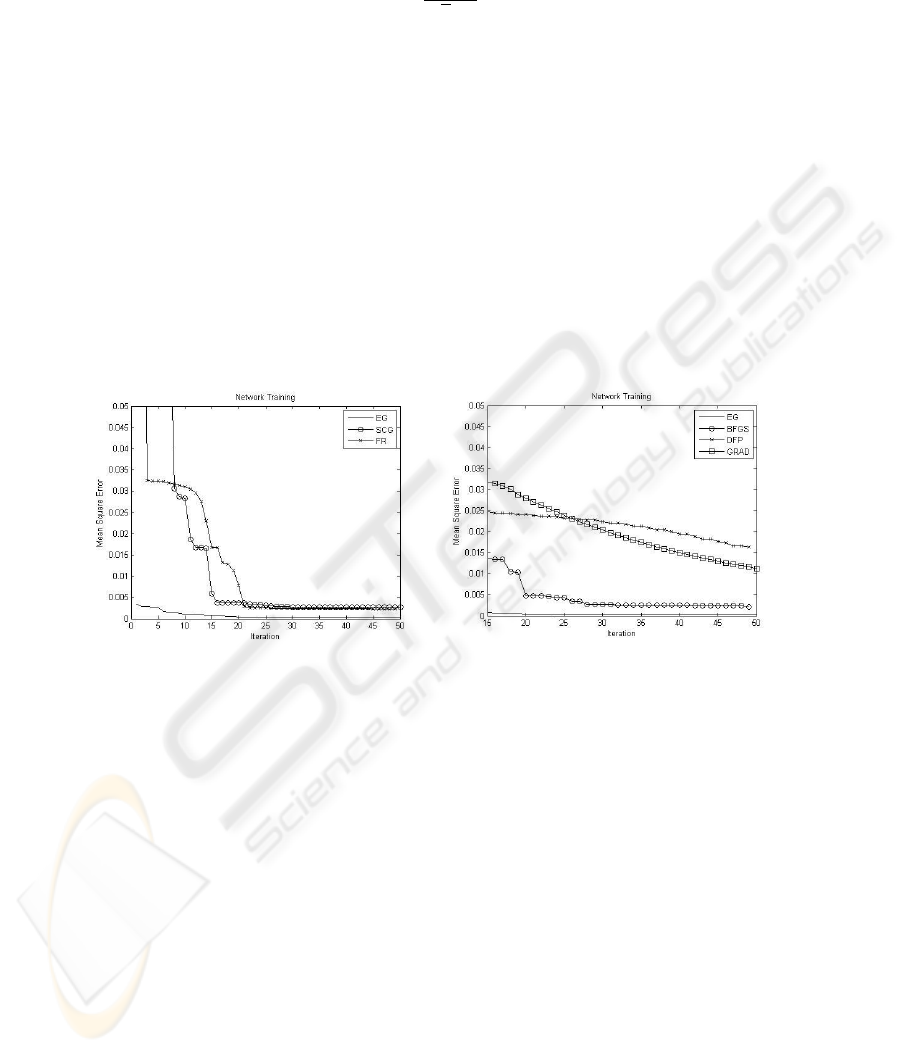
Fig. 1. EG SCG FR.
Fig. 2. EG BFGS DFP GRAD.
In a first test, seeking to compare the efficiency of the EG compared to the previ-
ously mentioned methods, a ANN containing 3 neurons in its hidden layer was used,
having the configuration: 3-3-1. The result of the network training can be visualized in
the Fig.1 and Fig.2.
Given the stochastic characteristic of the EG, these figures show its average behavior
for a total of 20 repetitions of the training process. For this example the EG presented
quite superior results when compared with the procedural methods.
Another important analysis is to compare the result of the ANN training by evolv-
ing gradient the method with the using the genetic algorithm directly for obtaining the
optimum vector θ by minimizing the error surface.
For accomplish this analysis, let us consider a genetic algorithm, GA, with the same
number of individuals of the EG. This algorithm is applied to search for parameters
vector through 100 iterations while the EG algorithm had accomplished 5 epoc with
20 iterations per epoc, what gives for both methods the same number of iterations. The
8

optimization process was repeated 20 times, and the average values for the ANN error
as shown in Figure 3.
Fig. 3. Network Learning: EG × GA. Fig. 4. Network Learning Diversity.
Figure 3 shows the superiors results obtained by the EG.
An analysis also relevant in this study, is to verify the populations diversity in both
methods, what together with the results above, gives an more accurate understanding
about the search mechanism. The metric here chosen to measure the diversity value, is
the variance of the individuals fitness. Figure (5) shows the average value of diversity
for both methods in each iteration
3
of the training process.
Is clearly in Figure 3 the superior diversity preservation present by the EG. Differing
from the GA algorithm, the EG one do not present a significant lost of diversity after
some iterations.
In spite of to providing a significant reduction of the network mean square error at
each iteration, the EG is quite onerous from the computational cost viewpoint, given
that an evolution process should be completed at each epoc. In that way, the execution
of the algorithm may become too slow, depending of its configuration.
In [12], the author proves the superiority of the method SCG about the other meth-
ods here analyzed, due to the need of unidimensional search required by most methods,
that has computational cost O(N
2
) per iteration. The SCG method presents a compu-
tational cost: O(2N
2
) per iteration, what is very inferior to the ones of the methods
GRAD, DFP, BFGS and FR that possess computational costs:
4
O(31N
2
).
The EG method, presents a total cost O(n
i
n
p
N
2
) (using the same analysis of [12]),
that can become quite superior to the ones of the other methods depending on the choice
of n
i
and n
p
. However, the fast convergence of the method, compensate this high com-
putational cost. Figure 5 illustrates a simple comparison of the temporary evolution of
the SGC method with the evolving gradient method, for the network configuration: 3-9-
9-1 containing two hidden layers. For the SCG method 500 iterations were made while
3
Here iteration is used to describe the intermediate steps of training processes, and one iteration
of main process, of the EG, is referred as epoc
4
This value is due to the fact that the unidimensional search to makes 30 iterations for each
iteration make for the training method
9

for the EG method only 5 iterations were made, to compensate the difference between
the computational costs.
Fig. 5. Network Learning.
The EG, in spite of being computationally onerous, has a quite fast convergence,
and in some cases this characteristic compensates its high computational cost, as in the
situation shown in the Figure 5. Due the stochastic characteristic present in the EG and
also in the training initialization, is not possible to conclude that the EG algorithm is
faster than the SCG method in all cases, however, the result in Figure5 let us to state
that the EG method is competitive with the other methods, from the learning efficiency
viewpoint.
4.2 Curve Fitting
In this example a group of 100 test samples of input-output pairs was used for a quadratic
function y = x
2
, where a white noise of width 10
−4
was inserted in both signs (input
and output). The training was accomplished for various networks configurations, using
the EG and the algorithms previously mentioned. The results can be observed in Tables
1 and 2.
Table 1. Learning Results: EG SCG FR.
Architecture EG SCG FR
1-3-1 0.00019 0.00066 0.00030
1-6-1 0.00022 0.00069 0.00031
1-9-1 0.00020 0.00078 0.00033
1-18-1 0.00024 0.00082 0.00035
1-6-6-1 0.00029 0.01065 0.01395
1-12-12-1 0.00019 0.01135 0.01735
1-6-12-6-1 0.00023 0.00667 0.05779
1-12-18-12-1 0.00014 0.01764 0.06142
10

Table 2. Learning Results: BFGS DFP GRAD.
Architecture BFGS DPF GRAD
1-3-1 0.00032 0.00079 0.01012
1-6-1 0.00037 0.00529 0.01197
1-9-1 0.00039 0.00617 0.01207
1-18-1 0.00045 0.00657 0.01287
1-6-6-1 0.01161 0.00959 0.01342
1-12-12-1 0.00943 0.00993 0.01377
1-6-12-6-1 0.00070 0.01060 0.01398
1-12-18-12-1 0.00420 0.01254 0.01485
For this problem it is also possible to notice that the final errors for the EG, was also
quite inferior to the ones of the others tested algorithms. Another outstanding charac-
teristic observed in the exposed results is the robustness of the EG method with respect
to variations in the ANN topology. Due the stochasticity of the learning process, it is
possible to infer that the EG method has presented the same final errors results for the
several tested configurations.
5 Conclusions
The method proposed in this paper represents a new approach for MLP artificial ANNs
training using meta-heuristic methods, presenting some new features with respect to
others similar methods.
The use of genetic algorithms in ANN training was until now, not competitive given
the inferior performance of these methods when compared to procedural optimization
techniques. This new approach, however, is competitive in this scenery, reaching results
comparable with the ones of the usual methods of ANN training, and still preserving
some characteristics of the heuristic methods.
One of the main advantages of the evolving gradient method, is the possibility to
train ANNs with the same efficiency of methods as BFGS and SCG, without the error
gradient, enlarging its application to another several problems, as the one proposed in
[3],[2].
The high computational cost, characteristic of heuristic methods as the genetic al-
gorithms, also is present in the EG that is more onerous that the other methods here
discussed. However, it is clear in the shown examples, that this high computational cost
is compensated by the accelerated convergence rate of EG method, turning its tempo-
rary evolution, comparable to any one of the others training algorithms here discussed.
Moreover, the computational cost here analysed is related to a digital machine,
which is the tool today available, however, the intrinsic parallelism of the EG, allows
its an implementation in a hypothetical parallel machine, that can be several orders of
magnitude faster than the procedural methods here discussed, inherently sequential.
So we may conclude that the Evolutionary Gradient method here presented, rep-
resents a viable alternative solution for artificial ANNs training in several situations,
especially in more complex applications, mainly when the construction of the gradient
vector is difficulty or even impossible.
11

References
1. R. Battiti and F. Masulli. Bfgs optimization for faster and automated supervised learning.
INNC 90 Paris, International Neural Network Conference,, pages 757–760, 1990.
2. Csar Dalto Berci. Observadores Inteligentes de Estado: Propostas. Tese de Mestrado,
LCSI/FEEC/UNICAMP, Campinas, Brasil, 2008.
3. Csar Dalto Berci and Celso Pascoli Bottura. Observador inteligente adaptativo neural no
baseado em modelo para sistemas no lineares. Proceedings of 7th Brazilian Conference on
Dynamics, Control and Applications. Presidente Prudente, Brasil, 7:209–215, 2008.
4. J
¨
urgen Branke. Evolutionary algorithms for neural network design and training. In 1st Nordic
Workshop on Genetic Algorithms and its Applications, 1995. Vaasa, Finland, January 1995.
5. D.J. Chalmers. The evolution of learning: An experiment in genetic connectionism. Pro-
ceedings of the 1990 Connectionist Summer School, pages 81–90, 1990.
6. Charles Darwin. On the Origin of Species by Means of Natural Selection, or the Preservation
of Favoured Races in the Struggle for Life. John Murray, London, 1859.
7. D.C. Dennett. Darwin’s Dangerous Idea: Evolution and the Meanings of Life. Penguim
Books, 1995.
8. A. Fiszelew, P. Britos, A. Ochoa, H. Merlino, E. Fernndez, and R. Garca-Martnez. Finding
optimal neural network architecture using genetic algorithms. Software & Knowledge Engi-
neering Center. Buenos Aires Institute of Technology. Intelligent Systems Laboratory. School
of Engineering. University of Buenos Aires., 2004.
9. C. Fyfe. Artificial Neural Networks. Department of Computing and Information Systems,
The University of Paisley, Edition 1.1, 1996.
10. D.G. Luenberger. Linear and Nonlinear Programming. Addison-Wesley, 2nd edition, 1984.
11. M.F. Mller. Learning by conjugate gradients. The 6th International Meeting of Young Com-
puter Scientists, 1990.
12. M.F. Mller. A scaled conjugate gradient algorithm for fast supervised learning. Computer
Science Department, University of Aarhus Denmark, 6:525–533, 1990.
13. D. Montana and L. Davis. Training feedforward neural networks using genetic algorithms.
Proceedings of the International Joint Conference on Artificial Intelligence, pages 762–767,
1989.
14. D. E. Rumelhart, R. Durbin, R. Golden, and Y. Chauvin. Backpropagation: The basic theory.
Lawrence Erlbaum Associates, Inc., 1995.
15. D. E. Rumelhart, G. E. Hinton, and R. J. Williams. Learning internal representations by
error propagation, in: Parallel distributed processing: Exploration in the microstructure of
cognition. Eds. D.E. Rumelhart, J.L. McClelland, MIT Press, Cambridge, MA., pages 318–
362, 1986.
16. Udo Seiffert. Multiple layer perceptron training using genetic algorithms. ESANN’2001
proceedings - European Symposium on Artificial Neural Networks, pages 159–164, 2001.
17. Zhi-Hua Zhou, Jian-Xin Wu, Yuan Jiang, and Shi-Fu Chen. Genetic algorithm based selec-
tive neural network ensemble. Proceedings of the 17th International Joint Conference on
Artificial Intelligence., 2:797–802, 2001.
12
