OBSTACLE AVOIDANCE FOR AUTONOMOUS MOBILE
ROBOTS BASED ON POSITION PREDICTION
USING FUZZY INFERENCE
Takafumi Suzuki
Graduate School of Science and Technology, Keio University, 3-14-1, Hiyoshi, Kohoku-ku, Yokohama 223-8522, Japan
Masaki Takahashi
Department of System Design Engineering, Faculuty of Science and Technolog
Keio University, 3-14-1, Hiyoshi, Kohoku-ku, Yokohama 223-8522, Japan
Keywords: Autonomous Mobile Robot, Obstacle Avoidance, Fuzzy Potential Method, Omni-directional Mobile Robot.
Abstract: This study presents an obstacle avoidance method for Autonomous Mobile Robot by Fuzzy Potential
Method (FPM) considering velocities of obstacles relative to the robot. The FPM, which is presented by
Tsuzaki, is action control method for autonomous mobile robot. In the proposed method, to decide a
velocity vector command of the robot to avoid moving obstacles safely, Potential Membership Function
(PMF) considering time until colliding and relative velocity is designed. By means of considering predicted
positions of the robot and the obstacle calculated from the time and the relative velocity, the robot can start
avoiding behaviour at an appropriate time according to the velocity of the obstacle and the robot. To verify
the effectiveness of the proposed method, numerical simulations and simplified experiment intended for an
omni-directional autonomous mobile robot are carried out.
1 INTRODUCTION
In the future, it’s not difficult to image that we will
often come across many autonomous mobile robots
traversing densely populated place we live in. In
such situation, because the autonomous mobile
robots need to carry out their tasks in a place with
unknown obstacles, the obstacle avoidance is one of
the important functions of the robots. With a view to
implementation of autonomous mobile robot
working in doors, we employ an omni-directional
platform as shown in Figure 1(a). For experimental
verification, an omni-directional mobile robot shown
in Figure 1(b) is developed. The robot has an omni-
directional camera for environmental recognition,
and can move to all directions by four omni wheels.
While there are many studies about obstacle
avoidance method focusing attention on possibility
of avoidance, this paper presents the method
focusing on not only possibility but also safer
trajectory of avoidance. Even if there are the same
situations that the robot needs to avoid a static
obstacle, timing of beginning avoidance behaviour
should vary according to the robot speed. If the
obstacles are moving also, the timing should vary
according to the velocities of the obstacles. To cite a
case, in a situation that a robot and an obstacle go by
each other as shown in Figure 2, the robot should
avoid along the curved line like (iii) according to the
speeds of the obstacle and own speed. To get to the
goal with efficient and safe avoidance behaviour in
the unknown environment for the robots, predicting
the future obstacles’ position by their current
(a) (b)
Figure 1: An omni-directional platform of a prototype
robot (a) and an example of a situation that the robot needs
to avoid the other robot (b).
299
Suzuki T. and Takahashi M. (2009).
OBSTACLE AVOIDANCE FOR AUTONOMOUS MOBILE ROBOTS BASED ON POSITION PREDICTION USING FUZZY INFERENCE.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 299-304
DOI: 10.5220/0002217102990304
Copyright
c
 SciTePress

y
x
Robot
Robot
Obstacle
Obstacle
Goal point
Goal point
(i)
(i)
(ii)
(ii)
(iii)
(iii)
y
x
y
x
Robot
Robot
Obstacle
Obstacle
Goal point
Goal point
(i)
(i)
(ii)
(ii)
(iii)
(iii)
Figure 2: Example of a situation of obstacle avoidance.
0
180−
180
direction
direction
[deg]
[deg]
1
0
μ
μ
0
180−
180
direction
direction
[deg]
[deg]
1
0
μ
μ
0
180−
180
direction
direction
[deg]
[deg]
1
0
μ
μ
0
180−
180
direction
direction
[deg]
[deg]
1
0
μ
μ
0
180−
180
direction
direction
[deg]
[deg]
1
0
μ
μ
0
180−
180
direction
direction
[deg]
[deg]
1
0
μ
μ
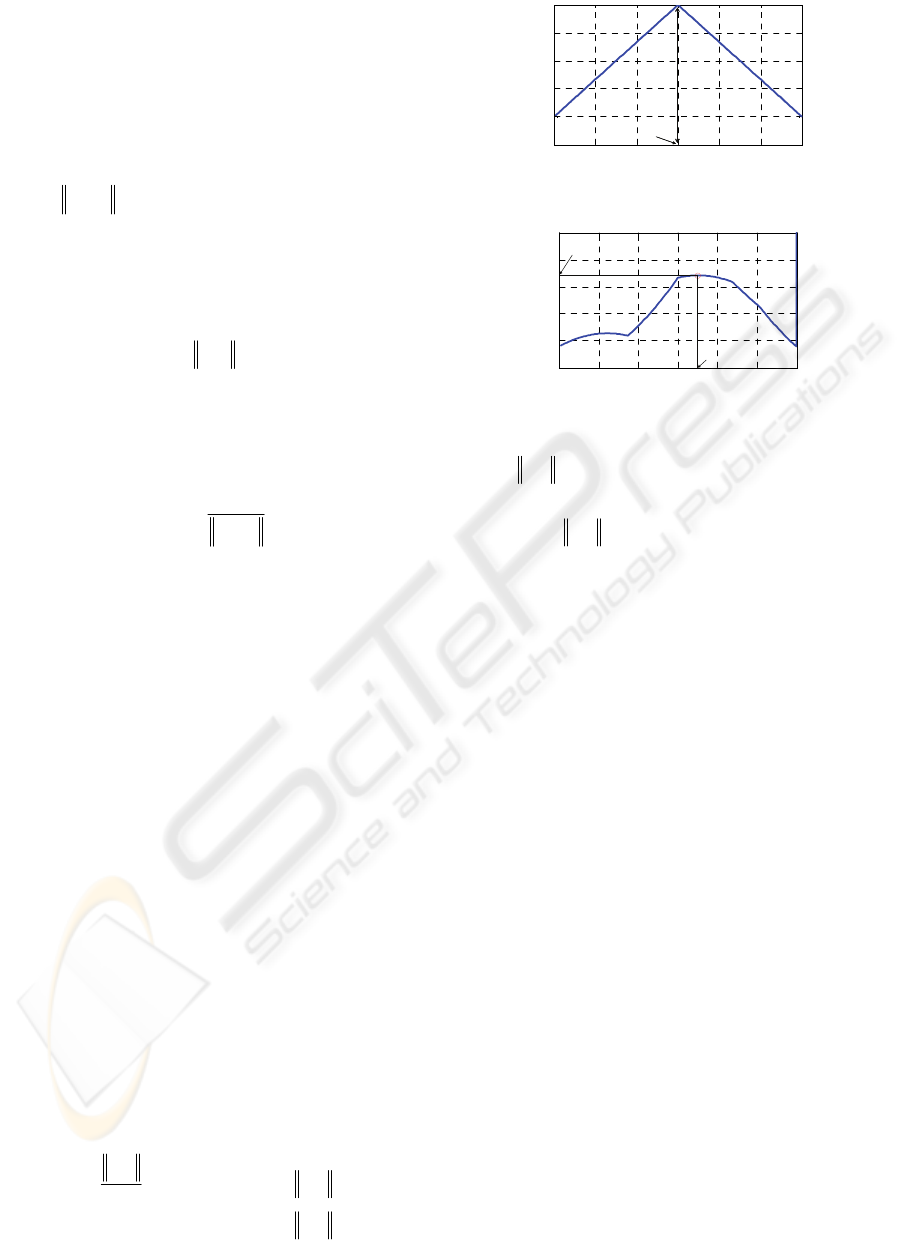
Figure 3: Example of PMF.
movements is needed. This paper introduces a real-
time obstacle avoidance method introducing the
velocity of obstacle relative to the robot. By means
of considering predicted positions of the robot and
the obstacle calculated from the time and the relative
velocity, the robot can start avoiding behaviour at an
appropriate time according to the velocity of the
obstacle and the robot. Some researches focus
attention on the velocity of obstacle (Ko et al., 1996)
to avoid moving obstacles efficiently. In this
research, virtual distance function is defined based
on distance from the obstacle and speed of obstacle,
however, only projection of the obstacle velocity on
the unit vector from the obstacle to the robot is
considered. In other words, the velocity of the robot
is not considered. On the other hand, in (Ge et al.,
2002), the velocity of the obstacle relative to the
robot is considered. Our approach also employs the
relative velocity. In addition to this approach, a
position vector of the obstacle relative to the robot in
the future is calculated by the relative position and
the velocity. To solve the real-time motion planning
problem, fuzzy potential method (FPM) is proposed
by Tsuzaki (Tsuzaki et al., 2003). In this research,
the method is applied to autonomous mobile robot
which plays soccer. By adequate designing of
potential membership function (PMF), it is realized
that wheeled robots can get to the goal with
conveying a soccer ball and avoiding obstacles. This
method is easy to understand at a glance. However,
in dynamic environment, to avoid moving obstacles
efficiently, more specific guideline of designing is
desired. In this paper, we introduce design method
of PMF considering the predicted positions and
discuss the availability by comparing the design of
PMF considering the relative velocity and that not
considering.
δ
out
v
2
w
v
1
w
v
4
w
v
3
w
v
x
r
v
y
r
v
φ

out
θ
L
δ
out
v
2
w
v
1
w
v
4
w
v
3
w
v
x
r
v
y
r
v
φ

out
θ
LL
Figure 4: An omni-directional platform.
2 FUZZY POTENTIAL METHOD
(FPM) FOR
OMNI-DIRECTIONAL
PLATFORM
In the Fuzzy Potential Method (FPM), a recent
command velocity vector considering element
actions is decided. Element actions are represented
as Potential Membership Functions (PMFs), and
then they are integrated by means of fuzzy inference.
Furthermore, by using a state evaluator, the PMFs
are modified adaptively according to the situation.
The directions on the horizontal axis in Figure 3
correspond to the directions which are from -180 to
180 degrees and measured clockwise from the front
direction of the robot. The priority for the direction
is represented on the vertical axis. By use of the
priority, direction and configured maximum and
minimum speed, the current command velocity
vector
out
v is calculated. The command velocity
vector is realized by four DC motors and omni
wheels using following equations:
cos
x
r out out
v
θ
= v
(1)
sin
y
r out out
v
θ
= v
(2)
1
2
3
4
cos sin
cos sin
cos sin
cos sin
w
x
r
w
y
r
w
w
L
v
v
L
v
v
L
v
L
v
δδ
δδ
δδ
φ
δδ
⎛⎞
⎛⎞
⎛⎞
⎜⎟
⎜⎟
−−
⎜⎟
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
−−
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎜⎟
−−
⎝⎠
⎝⎠

(3)
where
out
v and
φ

are respectively current command
velocity vector and rotational speed.
δ
is an angle
of gradient for each wheel.
L is a half of a distance
between two catawampus wheels.
w
i
v is a command
movement speed of each
-thi wheel.
PMF idea allows us to represent our knowledge
and experiences easily, and furthermore it gives us
easy understanding. The priority can be seen as a
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
300

desire for each direction of the robot. In this paper,
to discuss an obstacle avoidance problem, methods
for generating of PMF to head to the goal and to
avoid moving obstacles are introduced. This method
has two steps. First step is generating PMFs. Second
step is deciding the command velocity vector by use
of fuzzy inference to integrate the PMFs.
Hereinafter, design method of PMF considering the
obstacle velocity relative to the robot and way to
decide the command velocity vector by fuzzy
inference are described.
y
x
Robot
Obstacle
Predicted coordinate
Goal point
,_ro p
θ
φ
,_ro p
r
α
y
x
y
x
Robot
Obstacle
Predicted coordinate
Goal point
,_ro p
θ
φ
,_ro p
r
α
Figure 5: Predicted coordinate.
3 FPM CONSIDERING THE
RELATIVE VELOCITY
To realize the obstacle avoidance in dynamic
environment, the proposed method employs two
different PMFs, one is considering the velocity of
obstacle relative to the robot, the other is to head to
the goal. PMF is denoted by
μ
which is function of
θ
. Note
θ
is the direction from -180 to 180 degrees
measured clockwise from front direction of the
robot. To simplify the analysis, it is assumed that the
autonomous mobile robots detect obstacles by
equipped external sensors and are capable of
calculating the positions and velocities of obstacles
relative to the robot. The shapes of the robot and the
obstacles are treated as circles on 2D surface.
3.1 Design of PMFs
3.1.1 PMF for an Obstacle
To avoid moving obstacles safely and efficiently, an
inverted triangular PMF by specifying a vertex,
height and base width is generated. Because this
PMF considers future positions of the robot and the
obstacle, the robot can start avoiding the obstacle
early and be prompted not to go on to the future
collision position. For the purpose of safe avoidance,
the PMF
o
μ
is generated.
First, to predict the future state of both the obstacle
and the robot with the aim of efficient avoidance, a
-180 -120 -60 0 60 120 180
0
0.2
0.4
0.6
0.8
1
θ
[deg]
p[-]
a
[deg] θ
μ
o
1.0
,_ro p
θ
b
-180 -120 -60 0 60 120 180
0
0.2
0.4
0.6
0.8
1
θ
[deg]
p[-]
a
[deg] θ
μ
o
1.0
,_ro p
θ
b
Figure 6: PMF for obstacle considering relative velocity.
predicted relative position vector, in
T
γ
seconds,
,_ _ _
(r ,r )
ro p x p y p
=
r
is calculated as following
equation:
,_ , ,ro p ro ro
T
γ
=
+rrv
(4)
where
,
(r ,r )
ro x y
=
r is current position vector of the
obstacle relative to the robot, and
,
(v ,v )
ro x y
=v is
the current velocity vector of obstacle relative to the
robot.
γ
is an arbitrary parameter from 0 to 1.
T
,which is the time until the distance between the
obstacle and the robot is minimum, is defined as
following equation:
,
,
ro
ro
T
−
=
r
p
v
(5)
where
(p ,p )
x
y
=
p is a position vector of the
obstacle relative to the robot when a distance in the
future between the obstacles and the robot is
minimum.
p is calculated by means of relative
position and velocity vector as following equation:
{
}
(v v )r r (v v v v )
p
p
(v v )p
yxy x yx xy
x
y
yxx
⎛⎞
−+
⎛⎞
⎜⎟
=
⎜⎟
⎜⎟
−
⎝⎠
⎝⎠
(6)
As described above, the predicted relative position
vector, at the time
T
γ
seconds from now,
,_ro p
r is
calculated as Figure 3 shows. By use of this position
vector, a predicted obstacle direction relative to the
robot
,_ro p
θ
is calculated as following:
_
,_
_
r
arctan
r
yp
ro p
xp
θ
⎛⎞
=
⎜⎟
⎜⎟
⎝⎠
(7)
where,
,_ro p
θ
is decided to be the vertex of the
inverted triangle.
Next, as a measure to decide how far the robot
should depart from the obstacle,
a is defined as the
height of the inverted triangular PMF.
a is
described as following equation:
,_
,_
,
ro p
ro p
ro
aif
R
α
α
α
−
=
<
−
r
r
(8)
,ro r o
RRR
=
+
(9)
OBSTACLE AVOIDANCE FOR AUTONOMOUS MOBILE ROBOTS BASED ON POSITION PREDICTION USING
FUZZY INFERENCE
301

where
r
R and
o
R denote respectively the radius of
the robot and that of the obstacle treated as circles. If
the calculated obstacle position at
T
γ
seconds later
is inside of a circle with radius
α
from the robot
position at
T
γ
seconds later, the PMF for obstacle
avoidance considering the relative velocity is
generated. In other words, if a predicted relative
distance
,_ro p
r is below
α
, a is defined and the
inverted triangular PMF corresponding to the
obstacle is generated. Smaller the predicted relative
distance is, larger the value of
a is.
In addition, a base width of inverted triangular
PMF is decided by following equation:
,ro
b
η
φ =+v
(10)
where
φ
is decided based on the sum of radiuses of
the robot and the obstacle, and predicted relative
position vector as Figure 3 shows.
φ
is calculated
by following equation:
,
,_
arcsin
ro
ro p
R
φ
⎛⎞
⎜⎟
=
⎜⎟
⎝⎠
r
(11)
b increases up to
π
[rad] in proportion to an
absolute value of the relative velocity and predicted
relative distance. If the obstacle comes at rapidly, for
instance, the value of
b
increases. Hence, the base
width grows shown in Figure 4, and the value of
priority for the direction of the obstacle relative to
the robot comes about to be reduced.
η
is a gain.
As mentioned above, by deciding the vertex, the
height and the base width of inverted triangle
considering the predicted relative position, PMF
o
μ
,
which aims to early starting of avoidance behavior
and prompt the direction of the velocity vector to be
far from obstacle direction in response to the fast-
moving obstacle, is generated.
3.1.2 PMF for a Goal
To head to the goal, a PMF
d
μ
shaped like triangle
as shown in Figure 5. As a measure to decide how
much the robot want to head to the goal,
c
is
defined as the height of the triangular PMF.
c
gets
the maximum value at an angle of the goal direction
relative to the front direction of the robot,
d
θ
, and is
described as following equation:
,
,
,
1.0
rd
rd
rd
if
c
if
ε
ε
ε
⎧
≤
⎪
=
⎨
⎪
>
⎩
r
r
r
(12)
-180 -120 -60 0 60 120 180
0
0.2
0.4
0.6
0.8
1
θ
[deg]
p[-]
[deg]
θ
c
1.0
μ
d
d
θ
-180 -120 -60 0 60 120 180
0
0.2
0.4
0.6
0.8
1
θ
[deg]
p[-]
[deg]
θ
c
1.0
μ
d
d
θ
[deg]
θ
c
1.01.0
μ
d
d
θ
Figure 7: PMF for a goal point.
-180 -120 -60 0 60 120 180
0
0.2
0.4
0.6
0.8
1
θ
[deg]
p[-]
()
mix out
μθ
[deg] θ
out
θ
1.0
μ
mix
-180 -120 -60 0 60 120 180
0
0.2
0.4
0.6
0.8
1
θ
[deg]
p[-]
()
mix out
μθ
[deg] θ
out
θ
1.01.0
μ
mix
Figure 8: Mixed PMF.
where
,rd
r is an absolute value of the position
vector of the goal relative to the robot.
ε
is
constant. If
,rd
r is below
ε
, c is defined. The
shorter the distance between the obstacle and the
robot is, the smaller
c becomes. Therefore the robot
can decelerate and stop stably.
3.2 Calculation of Command Velocity
Vector by Fuzzy Inference
The proposed method employs fuzzy inference to
calculate the current command velocity vector.
Specifically, The PMF
o
μ
, which considers the
velocity of obstacle relative to the robot, and the
PMF
d
μ
, which is to head to the goal, are integrated
by fuzzy operation into a mixed PMF
mix
μ
as shown
in Figure 6.
mix
μ
is an algebraic product of
o
μ
and
d
μ
as following equation:
mix d o
μ
μμ
=
⋅ (13)
Finally, by defuzzifier, the command velocity
vector is calculated as a traveling direction
out
θ
and
an absolute value of the reference speed of the robot
base on the mixed PMF
mix
μ
.
out
θ
is decided as the
direction
i
θ
which makes a following function
()f
θ
maximum.
() ( )
jn
mix i
ijn
f
θ
μθ
+
=−
=
∑
(14)
where
n is the parameter to avoid choosing
undesirable
i
θ
caused by such as noises on the
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
302

-180 -120 -60 0 60 120 180
0
0.2
0.4
0.6
0.8
1.0
theta[deg]
u[-]
μ
direction [deg]
Robot PMF
Desired direction
Robot PMF
Desired direction
-180 -120 -60 0 60 120 180
0
0.2
0.4
0.6
0.8
1.0
theta[deg]
u[-]
μ
direction [deg]
-180 -120 -60 0 60 120 180
0
0.2
0.4
0.6
0.8
1.0
theta[deg]
u[-]
μ
direction [deg]
Robot PMF
Desired direction
Robot PMF
Desired direction
Figure 9: Visualization of PMF.
sensor data. Based on
out
θ
,
out
v is calculated as
following equation:
()
(
)
out mix out max min min
vvvv μθ =−+ (15)
where
()
mix out
μθ is the mixed PMF
mix
μ
corresponding to the
out
θ
,
max
v and
min
v are
configured in advance respectively as higher and
lower limit of the robot speed.
3.3 Visualization for PMF on
Two-dimension Surface
It would be convenient to have a visualizer that
show us why the robot will go on to the direction. In
the proposed method, we can see aspects of the PMF
on two dimension surface and understand easily the
reason for choice of the direction. For example, a
PMF described on polar coordinate shown in Figure
9(a) is comparable to the PMF described on x-y
coordinate shown in Figure 9(b).
4 SIMULATION RESULTS
The radius of robot and obstacle are supposed to be
both 0.3m, therefore,
,
0.6m
ro
R = .
α
in equation
(8) is 1.6m.
γ
in equation (4) is 0.7.
ε
in equation
(12) is 1.0m.
Figure 10, 11 and 12 show the simulation results
when the robot passes the obstacle. Initial positions
of the robot and the obstacle are respectively
(0m,0m) and (5.0m, 0.3m) . The goal position of
the robot is
(7.0m,0m) . In the situation in Figure 10,
the higher limit of robot speed is
max
0.5m/sv = , the
lower one is
min
0.0m/sv = . The higher limit of
acceleration of the robot is
2
1.0m/s
r
a = . The
simulations have done with three different obstacle
speed
0.0, 0.5m/s
o
v = , that the direction is negative
on
x
-axis. Figure 10(a) and (b) show respectively
the trajectory of the robot that the PMF for obstacle
avoidance is generated without considering the
relative velocity and that with considering the
relative velocity, when
0.0m/s
o
v
=
. In Figure 10(a),
-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Robot : 10.8s
Robot : 15.0s
Robot : 0.0s
Robot : 19.0s Robot : 19.5s
-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Robot : 10.8s
Robot : 15.0s
Robot : 0.0s
Robot : 19.0s Robot : 19.5s
(a) not using PMF considering relative velocity
-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Robot : 3.1s Robot : 12.6s
Robot : 0.0s
Robot : 15.0s Robot :20.6s
-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Robot : 3.1s Robot : 12.6s
Robot : 0.0s
Robot : 15.0s Robot :20.6s
(b) using PMF considering relative velocity
Figure 10: Simulation results of an obstacle avoidance
going by each other when speed of obstacle (
o
v )
is
0.0m/s
and of a robot (
r
v ) is
0.5m/s
.
-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Robot : 1.9s Robot : 8.5s
Robot : 0.0s
Robot : 10.8s Robot :13.2s
-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Robot : 1.9s Robot : 8.5s
Robot : 0.0s
Robot : 10.8s Robot :13.2s
Figure 11: Simulation results of an obstacle avoidance
going by each other when speed of obstacle (
o
v )
is
0.0m/s and of a robot (
r
v ) is 0.8m/s.
the robot gets close to the obstacle because the
relative velocity is not considered. On the other
hand, in Figure 10(b), the early starting of avoidance
behaviour due to generating PMF by use of
predicted information based on the relative velocity.
In addition to the situation as in Figure 10(b), in
Figure 11, the higher limit of the robot speed has
been changed:
max
0.8m/sv
=
. Even if the robot
speed becomes more rapid, the robot succeed in
efficient avoidance. In Figure 12(a) and (b), the
trajectories of the robot, with PMF considering the
relative velocity and not considering that, when the
obstacle speed
0.5m/s
o
v
=
. In (a), due to delay of
starting avoidance behaviour, the robot collided with
the obstacle. On the other hand, in (b), due to the
early starting of the avoidance behaviour, the robot
succeeded at the obstacle avoidance.
From these simulation results, it is confirmed that
by an associating the PMF for avoidance with the
relative velocity, faster the obstacle speed is, earlier
the timing of the avoidance behaviour of the robot is,
therefore the ability of avoiding obstacle can be
enhanced.
OBSTACLE AVOIDANCE FOR AUTONOMOUS MOBILE ROBOTS BASED ON POSITION PREDICTION USING
FUZZY INFERENCE
303

-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Obstacle : 0.0s
Obstacle : 4.1sObstacle : 5.3s
Robot : 4.1s Robot : 5.3s
Robot : 0.0s
Robot : 15.0s
Robot : 18.8s
-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Obstacle : 0.0s
Obstacle : 4.1sObstacle : 5.3s
Robot : 4.1s Robot : 5.3s
Robot : 0.0s
Robot : 15.0s
Robot : 18.8s
(a) not using PMF considering relative velocity
-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Obstacle : 0.0s
Obstacle : 1.8sObstacle : 6.7sRobot : 0.0s
Robot : 1.8s Robot : 6.7s Robot : 15.0s Robot : 20.4s
-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
-1.0
0
1.0
x-coordinate [m]
y-coordinate [m]
Obstacle : 0.0s
Obstacle : 1.8sObstacle : 6.7sRobot : 0.0s
Robot : 1.8s Robot : 6.7s Robot : 15.0s Robot : 20.4s
(b) using PMF considering relative velocity
Figure 12: Simulation results of obstacle avoidance going
by each other when speed of an obstacle (
o
v ) is 0.5m/s
and of a robot (
r
v ) is 0.5m/s.
5 EXPERIMENTAL RESULTS
To verify the effectiveness of the proposed method
that employs PMF considering the velocity of the
obstacle of the robot, a ball is supposed to be a
moving obstacle and is rolled toward the robot. The
robot recognizes the environment by the omni-
directional camera. A position of a goal and that of
an obstacle relative to the robot are calculated by
extracting features based on objects’ colours. The
robot size is L 0.4
×
W 0.4
×
H 0.8m and the ball
diameter is 0.2m. The radius of robot and obstacle
are supposed to be 0.3m and 0.1m respectively,
therefore,
,
0.4m
ro
R = .
α
is set to 1.4m when the
robot uses the proposed PMF which is considering
relative velocity. When the robot doesn’t use the
proposed PMF,
α
is set to 2.4m.
γ
is 0.7.
ε
is
1.0m.
max
v is 0.5m/s,
min
v is 0.0m/s.
r
a is
2
1.0m/s .
When the robot used the proposed PMF, which was
considering relative velocity, as shown in Figure 13
(a), it succeeded in avoiding the moving ball with
smooth trajectory. On the other hand, in the situation
Figure 13 (b), the robot with the PMF, which was
not considering relative velocity, diverged once.
(a) (b)
Figure 13: Trajectories of the obstacle (ball) and the robot
with the PMF considering relative velocity (a) and not
considering relative velocity (b).
6 CONCLUSIONS
In this paper, design method of the potential
membership function (PMF), which is considering
the velocity of the obstacle relative to the robot for
the purpose of avoiding the moving obstacle safely
and smoothly, has been presented. In the proposed
method, the proposed PMF for an obstacle and PMF
for a goal are unified by fuzzy inference. By
defuzzification, the command velocity vector of the
robot is calcu lated and the obstacle avoidance has
realized. A numerical simulation, which assumes an
obstacle avoidance of autonomous omni-directional
mobile robot, has done. As the result of the
comparison between the design method of PMF
using relative velocity and not using, it is confirmed
that the ability of avoiding the moving obstacle can
be enhanced. In addition, thorough simplified
experiments, the real robot can avoid an obstacle
using proposed method.
REFERENCES
Khatib, O., 1986. Real-time Obstacle Avoidance for
Manipulators and Mobile Robots, In Int. J. of Robotics
Research, vol.5, no.1, pp.90-98.
Ge, S., S., and Cui, J., Y., 2002. Dynamic Motion
Planning for Mobile Robots Using Potential Field
Method, In Autonomous Robots, vol.13, pp.207-222.
Arkin, R., C., 1989. Motor schema-based mobile robot
navigation, In Int. J. Robotics Research, vol. 8, no. 4,
pp. 92-96.
Ko, Y., N., and Lee, H., B., 1996. Avoidability Measure in
Moving Obstacle Avoidance Problem and Its Use for
Robot Motion Planning, In Proc. of IEEE/RSJ Int.
Conf. on Intelligent Robots and Systems (IROS 96),
pp.1296-1303.
Borenstein, J., and Koren, Y., 1991. The Vector Field
Histogram Fast Obstacle Avoidance For Mobile
Robots, In IEEE Trans. on Robotics and Automation,
Vol.7, No.3, pp.278-288.
Fox, D., Burgard,W. and Thrun,S., 1997. The Dynamic
Window Approach to Collision Avoidance, In IEEE
Robotics and Automation, Vol. 4, No. 1, pp.1-23.
Tsuzaki, R., Yoshida , K., 2003. Motion Control Based on
Fuzzy Potential Method for Autonomous Mobile
Robot with Omnidirectional Vision. In Journal of the
Robotics Society of Japan . vol.21, no.6, pp.656-662.
Otsuka, F., Fujii, H., Yoshida, K.,,2005. Action Control
Based on Extended FPM for an Autonomous Mobile
Robot. The 26th Annual Conference of the Robotics
Society of Japan.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
304