Multi Project Organization Optimization

using Genetic Algorithm

Sven Tackenberg and Sebastian Schneider

Chair and Institute of Industrial Engineering and Ergonomics

RWTH Aachen University, Bergdriesch 27, Aachen, Germany

Abstract. Due to impatient customers and competitive threats, it has become

increasingly important to shorten the lead time of development projects and to

bring new products faster to the market. Furthermore, many organizations are

faced with the challenge of planning and managing the simultaneous execution

of multiple dependent projects under tight time and resource constraints. Within

that kind of business environment, effective project management and

scheduling is crucial to organizational performance. A genetic algorithm

approach with a novel genotype and GP mapping operation is proposed to

minimize the overall project duration and budget of multiple projects for a

resource constrained multi project scheduling problem (RCMPSP) without

violating inter-project resource constraints or intra-project precedence

constraints. Stochastic rework of tasks, variable assignment of actors and

stochastic makespan of a specific task are considered by the introduced GA.

The proposed Genetic Algorithm is tested on scheduling problems with and

without stochastic feedback. This GA demonstrates to provide a quick

convergence to a global optimal solution regarding the multi-criteria objectives.

1 Introduction

Challenges that are posed to an increasing number of companies are budget and

deadline overruns of development projects, missed specification, and therefore

customer and management frustration [11]. As a result, novel methods for identifying,

analyzing and optimizing the main performance shaping factors of development

projects as well as their interaction regarding complexity and coherence are necessary

[25].

Our vision is a novel approach to reduce the risk of multi-project management by

using optimization methods for multi-project planning to support project managers’

decision making. This concept should enable project managers to model, simulate and

optimize a work organization regarding their multi objective target system (cost, lead

time, utilization etc.) at each point of time during a development project. However, as

a consequence of the inherent complexity of development projects, [10] scientific

methods for a multi-criteria optimization of valid development project models are

missing. Based on results of the latest research, first results of a research project are

presented to close the identified gap between work process modeling and optimization

methods in order to continuously improve the performance of an organization’s

project portfolio.

Tackenberg S. and Schneider S. (2009).

Multi Project Organization Optimization using Genetic Algorithm.

In Proceedings of the 7th International Workshop on Modelling, Simulation, Veriﬁcation and Validation of Enterprise Information Systems, pages

101-115

DOI: 10.5220/0002219801010115

 SciTePress

The rest of the paper is organized as follows. In the next section, we review the

sequencing complexity of a project organization. Section 3 provides some background

of task scheduling and selected approaches for the systematical improvement of

project organizations due to optimization algorithms. The section 4 presents the

developed genetic algorithm. It comprises the GA structure as well as the

chromosome representation and initialization, the developed genetic operators and

especially the transformation of a chromosome representation into a specific project

organization model. To investigate the performance of the GA we discuss the results

of computational experiments for a project portfolio of an enterprise of the chemical

industry. Furthermore we evaluate the results of the proposed GA-based approach in

comparison to outcomes of a stochastic simulation model. The paper concludes with a

brief summary of the work completed, a critical acclaim and possible extension in

future.

2 Problem Complexity

The objective of a project manager is the prioritization of the precedence-constrained

tasks of a project to optimize an objective function such as minimizing project

duration or project costs. There are many possible objectives when considering a

resource-constrained project scheduling problem – RCPSP [15].

Therefore the scheduling problem for a multi project environment of a company – m

concurrent projects P

...P

, with a set of tasks TA

= {ta(1)...ta(n)}, where n specifies

the total number of tasks in project P

– is known as the resource-constrained multi

project scheduling problem (RCMPSP). The scheduling problem can be very complex

as the number of projects, tasks, actors and resources increases. It was shown by

Lenstra and Rinnooy (1978) that the scheduling of tasks under consideration of

precedence and resource constraints is NP-hard [5]. Due to the fact that a semi formal

project model can be transformed into a Design Structure Matrix – DSM [3] the

sequencing and assigning process can be formulated as a Quadratic Assignment

Problem (QAP). The QAP is well known as a NP-hard combinatorial optimization

problem [33]. Therefore at present no algorithm can be found to solve real-world

project models of arbitrary sizes for a multi project environment to optimality with an

adequate performance. A benchmark study done by Hartmann [9] demonstrated that a

project with as few as 60 activities has not been solved to the global optimum by

computational experiments. Furthermore additional projects can extremely enlarge the

number of feasible schedules. When considering the set of feasible project schedules

for a RCMPSP θ = θ

∩ θ

, where θ

denotes the set of precedent-feasible schedules

and θ

denotes the set of resource-feasible schedules, there exist many possible θ and

many potential objectives for choosing between them. Therefore it is important to

note, that the global optimum of θ is not compulsively based on the local optima of θ

and θ

102

3 Background

The design of a detailed feasible project organization in a multi-project environment

has been shown to be critical to the success of a development project [6].

Nonetheless, there is still a significant demand for fundamental research on planning,

execution and optimization of development projects [14]. Thus, project portfolio

managers are currently incapable to define effective and flexible project

organizations. The latter is basically caused by the high complexity of development

projects due to large degrees of freedom regarding the sequence of targets, the

assignment of actors and resources to targets, the occurrence of iterations as well as

types of cooperation, coordination and communication. Therefore substantiated and

comprehensive organizational models and methods for continuous improvement are

required [14]. However these have not yet been developed. Against this background,

the status of research in the field of optimization methods for development projects

will be reviewed in the following.

Project scheduling is of great practical significance, and generalized models can

be applied in product development, production planning as well as a variety of

scheduling applications. Early attempts at project scheduling were focused on

reducing the total project lead time (makespan) assuming unlimited resources. Well

known techniques include the Critical Path Method (CPM) [13] and the Project

Evaluation and Review Technique, PERT [22]. Scheduling problems have been

extensively studied for many years by attempting to establish precise solutions using

methods from the field of operations research [15].

It was shown that the general scheduling problem concerning precedence and

resource constraints is NP-hard [19]. Therefore, exact optimization methods are too

time consuming and ineffective for solving large organizational problems found in

real enterprises. Yang et al. [30] and Kolisch and Padman [15] surveyed the most

common methods that were developed for resource-constrained project scheduling

(RCPSP), such as dynamic programming, zero-one programming and implicit

enumeration with branch and bound.

Surveys of heuristic and metaheuristic approaches which solve intractable

problems quickly, efficiently and fairly satisfactorily can be found in Grünert and

Irnich [8] and Kolisch and Hartmann [17]. Nonobe and Ibaraki [24] developed a

technique to solve the RCPSP based on local search. Alternative approaches based on

tabu search and genetic algorithms were presented by Shouman et al. [26]. The

RCMPSP as a generalization of the RCPSP not only deals with the scheduling of one

project but also several projects. Each project is composed of a number of activities.

Goncalves et al. [7] solved multi-project instances consisting of up to 50 single

projects and 120 activities with a genetic algorithm (GA). The generation of solutions

of the RCMPSP based on GAs is also analyzed by Yassine et al. [31, 32]. Kolisch

[16], however, proposed a list scheduling algorithm. Due to its fast convergence and

easy implementation Linyi et al. [21] developed a particle swarm optimization. Their

study proved the results of former works that meta-heuristics are a promising

approach to project scheduling problems.

103

Fig 1. The GA structure.

4 Design and Implementation

This section introduces a novel GA to solve the RCMPSP. The probability of an

iterative execution of tasks during the project as well as stochastic values for the

duration of an activity can be also integrated in problem encoding.

4.1 GA Structure

Each chromosome consists of a collection of genes. Genes are placed at different

locations or loci of the chromosome and have values which are called alleles. The

characteristic of each gene of one chromosome is thereby represented by an allele.

The combination of genes (defined by loci and alleles) refers to the specific genetic

makeup of an individual, termed as genotype. While the genotype corresponds to the

structure of a GA, the term phenotype represents the decoded structure for the

RCMPSP – a specific project organization model which can be regarded as one point

in the search space. Classic genetic operations and functions as fitness function,

selection, crossover and mutation were adapted to our semi-formal description of

project models – C3 method [27] – to find optimal task sequences and assignments of

actors or tools for the predefined objectives.

The fitness function is used to evaluate a chromosome how good the underlying

project organization fulfils the multi criteria target system of a project manager. Next,

the function selection chooses chromosomes that will be passed on to the next

104

generation. To map the random process a crossover function is used to produce a new

offspring chromosome from minimum two parent chromosomes according to a user-

defined probability p

. If an offspring takes the best parts from each of its parents, the

result will likely be a better solution [31]. Modified as well as unmodified

chromosomes can be further mutated according to a user defined probability p

. The

mutation leads to a variability of the alleles regarding the characteristic of the project

organization. A new generation of chromosomes replaces the previous one, and the

fitness of the new generation is evaluated. The cycle of functions is repeated until a

termination condition is met, –number of generations or fitness convergence in the

population.

The novelty of the presented approach is the characteristic of a chromosome, the

evaluation of the fitness as well as the transformation of the modified chromosomes

into a detailed, feasible project organization model. Therefore we will focus on these

three aspects.

4.2 Data Structure

The sequence of tasks as well as the assignment of actors (workers, teams) and

resources (tools, machines, facilities) must be represented in a chromosome, which

describes the project organization model. Various representation models for encoding

a project as chromosomes in GAs exist, but the most common is the natural encoding

by integer numbers. Yassine et al. [31] and Zhuang et al. [33] introduce an encoding

where a specific element or sub-element of a project is assigned exactly once to a

locus in the permutation. Therefore each activity of a project is represented once in

the chromosome. From our point of view this encoding does not permit an extensive

and efficient permutation of a realistic complex project organization. Especially

uncertainties regarding the makespan of tasks, execution of iterations and restrictions

regarding the assignment of actors cannot be easily integrated in the encoding of a

project organization.

As shown in Figure 1 our approach introduces a novel representation of a project

organization as a chromosome to fulfill the requirements of an adequate project

representation. Each task of a project or multi project portfolio is given an unique

identification number (ID) and each gene represents a task. A gene therefore contains

information about the Task ID, ID of Actors and Resources, Period relating to the

ending time of the predecessor tasks, Stochastic factor for the makespan of an activity

and Occurrence of iteration. As shown in Figure 1 the structure of the gene is

mandatory. A representation technique is used where the location of each gene in a

chromosome is fixed and cannot be modified by genetic operators. The information

regarding the task and execution of activities is linked via pair representation <locus,

allele> – the locus of a gene is determined by the value of the corresponding task ID.

Due to the composition of a multi project organization based on genes the

chromosome length is set to the total task number of all considered projects.

Chromosomes and genes are linked to a central database which contains the static

values of the project portfolio specific actors, resources and iterations.

105

4.3 Objective Function

Every optimization method must be able to assign a measure of quality to generated

results in the search space to distinguish good and bad results [32]. For this purpose a

fitness function is used for GAs to assign each individual chromosome a fitness value.

To break down the RCMPSP it can be decomposed into a genotype-phenotype

mapping f

and a phenotype-fitness mapping f

[20, 32]. Therefore a genotypic

search space Φ

as well as a phenotypic search space Φ

exist which can be either

discrete or continuous. The genotypic search space Φ

covers all permutations of

chromosomes and genes. A feasibility function f

assigns each element in Φ

a value as

follows: f(x):Φ

→

{0,1}. According to the introduced decomposition, the genotype-

phenotype mapping occurs first, where feasible genotype elements (value = 1) are

mapped to elements in the phenotypic search space Φ

: f

) : Φ

→ Φ

(Sec. 4.6).

The result of the mapping is a feasible representation of a detailed project

organization. Subsequently, the fitness of a phenotype in Φ

is calculated by: f

→ ℜ. Thus, the fitness of an element is a result of both mappings: f = f

° f

= f

)) (see also [32]).

For the definition of f

essential objectives for the scheduling problem must be

considered. Based on the comprehensive survey by Kolisch and Padman [15] we

identified critical success factors for chemical engineering projects including

traditional ones such as project duration and cost minimization but also more recent

ones like the qualification of actors [12]. We use total project duration T, project cost

C as the RCMPSP multi criteria performance measure to be minimized and degree of

capacity utilization U to be maximized. So we use the following fitness function:

Minimize T = {∑d

+ p

| i = 1,...,n}

Minimize C = {∑c

| i = 1,2, …,n}

(1)

Maximize U = {∑u

| i = 1,2, …,n}

where t

is the starting time of task i

is the duration of task i

is the maximum time period between task i and its predecessors

is the cost of task / activity i

is the utilization of actor i

4.4 Constraints

The solution of the RCMPSP is subjected to the predecessor relationship between

tasks, described in the semi formal project model (C3 model). Due to the precedence

constraints of each project, each task needs to be checked if its immediate

predecessors have been sufficiently executed before being performed. Thereby a

complete fulfillment of a predecessor task is not mandatory. To integrate aspects of

Simultaneous Engineering (SE) an overlapping of coupled activities has been

considered in the GA. Therefore the precedence relationships are described by the

value “minimum percentage of completion” e

in the C3 model. The precedence

constraint can be formulated as:

106

min t

+ (d

× e

) ≤ t

i+1

, 0 < e

< 1 | 1,…,n

(2)

where e

represents the minimum percentage amount of work for task i to fulfill

the requirements for an execution of task i+1.

Although projects and tasks may be unrelated by precedence constraints, they

depend on a common pool of actors and resources. Due to the resource constraints

two actors or resource conflicting tasks ta

, ta

i+1

cannot be executed at the same time t:

+ d

≤ t

i+1

or t

i+1

+ d

i+1

≤ t

, | 1,…,n (3)

if a

(ta

) = a

(ta

i+1

) or r

(ta

) = r

(ta

i+1

is task i

is the actor i with a specific characteristic

is the resource i with specific functions

(ta

) is actor i assigned to task i.

Based on the task specific requirements at least one actor (worker, team) must be

assigned to a task. We assume that an actor and a resource must be devoted to an

activity until it is completed. An abort of an activity to start another activity is not

allowed. In contrast to the approaches of Zhuang et al. [33], KHosraviani [14] and

Yassine et al. [31, 32] the processing time d

and the actors a

and resources r

required

for any task ta

, a

(ta

); r

(ta

) are not fixed.

4.5 Initialization

Due to stochastic elements of the project model and several concurrent projects there

is only a small feasible search space. Therefore a random generation of alleles could

result in the generation of a large number of infeasible solutions [33]. Therefore a

permutation algorithm is used to generate an initial population of precedence feasible

individuals. This algorithm proceeds as follows:

Step 1: A task from one of the considered projects is randomly chosen. The task is

mapped to a gene:

- The gene is placed; task ID of the C3 model represents the locus.

- Values for the start time of an activity, the duration and the occurrence of an

iteration are calculated based on the database entries and the corresponding

probability distributions.

- Randomly an actor who fulfills the requirements (qualification, competence) is

chosen, and it is checked if the actor is already selected for the given period.

If the actor was selected before, continue this random selection until an

adequate actor is found. The assignment of resources is analogue.

Step 2: Repeat step 1 until the set of unselected tasks of all considered projects is

empty, which generates a chromosome that consists of all tasks.

Step 3: Repeat 1 and 2 until all chromosomes of a population size are generated.

The population size is determined by the project manager in consideration of the

problem complexity. To have an indication of an adequate population size Thierens

defined an equation necessary for a successful GA (1995). The equation was used by

us to get a first impression of the population size.

107

4.6 GP Mapping

A chromosome is a blueprint for a project organization. The genotype-phenotype

mapping f

– GP-mapping – is used to generate a feasible, detailed project

organization for each individual of a population. It results in a description of a project

organization which covers information about the characteristics and interactions of

tasks, the assignment of actors and resources to tasks as well as specific

characteristics of a detailed project scenario, i.e., concrete information regarding

starting time, makespans of activities, responsibilities etc. Attention should be paid to

the fact that a specific definition of a task sequence and responsibilities of actors does

not generate only one course of a project. Due to uncertainties regarding the required

effort to solve a task and the exact starting and ending time of an activity there exist

several courses of a project.

The GP Mapping operator acts to generate a project organization based on the

information of the varied or unvaried chromosomes and the data base entries. The

steps to this process are as follows:

Step 1: A task is randomly chosen and it is checked if its immediate predecessors

have been sufficiently executed before set in the project plan. If not, step 1 is

continued until a task is found.

Step 2: The makespan for the execution of a chosen task i is calculated, based on:

- Basic effort d

e(i)

of task i estimated by project managers without consideration

of actor’s qualification, (constant value for each specific task, stored in

database Activity)

- Qualification of assigned actor (constant value q, stored in database Actor)

- Random value h (variable value, stored in gene of the chromosome), based on

a task specific probability distribution, e.g., Gaussian, right- or left-skewed β-

distribution (constant parameters of the distribution are stored in database

Activity).

The makespan of task i is calculated as follows:

e(i)

× q × p

(4)

and is saved in the corresponding object of the class Chromosome.

Step 3: Calculation of the absolute starting time of activity i, based on:

- Period related to the ending time of the predecessor activities (variable factor

, saved in gene of the chromosome)

- Starting time and duration of the predecessor(s) saved in a LinkedHashMap

(temporary data base entry).

The absolute starting time of activity i is calculated as follows:

= t

i-1

+ (z

× d

i-1

)

(5)

The variance of value for z

is determined by the project manager, z

> 0. For

activities with more than one predecessor:

= max {

i-1

+ (c

× d

) | i = 2, …, n-1}

(6)

As an example, consider a chromosome with the two tasks ta

and ta

. Task ta

is the

predecessor of ta

and starts at the starting time 0 Time Units (TU) with a duration d

108

of 10 TU. The value for z

of task ta

(characteristic of the allele) is 0,4. Therefore 6

TU before finishing ta

is the earliest time to execute ta

(starting time: 4 TU).

Step 4: Assignment of an actor to a task, based on:

- Actor ID (variable value), stored in gene of the chromosome.

- Status of the actor (employed, unemployed) for the considered time period:

= t

+ d

(7)

The verification if an actor fulfills the minimum requirements of a task is

previously done during the mutation of a gene.

Step 5: Checking if the assigned actor executes another activity at any particular time

of the period p

. If the actor is unemployed the assignment leads to a change of status

(employed) of this actor for the period p

. If an actor is employed, the starting time of

the activity ta

is modified under consideration of predecessor conditions and the

earliest starting time, until a feasible solution is generated. In such a case the

equations 5 or 6 and 7 are re-executed until a valid solution is found.

Step 6: Task Freeze – the parameters of the considered task/activity are saved for the

current chromosome and cannot be modified again during this generation. The

activity is “placed” in the project plan.

Step 7: Repeat Steps 1 to 7 until all tasks of a chromosome have been placed to

generate a whole project organization.

It is important to note that different chromosomes may potentially have the same

fitness value and essentially represent the same project organization after the GP

mapping. Although uncertainties of development projects have been considered in the

GA, due to the novel genotype and GP Mapping the mapping of a specific genotype

into a phenotype produces always an identical project plan.

4.7 Selection

The selection pressure (SP) is defined as the number of expected individuals

(chromosomes) in the next generation and determines the performance of a selection

operator [1]. There are two popular types of selection approaches: fitness-

proportionate selection schemes and ordinal-based selection schemes. Fitness-

proportionate schemes may often fail to provide adequate SP when fitness variance in

the population is very high or very low [31].

Therefore an ordinal-based selection scheme – Tournament Selection [2] – is

employed in this algorithm because of its ability to ensure an adequate SP

independent of a specific fitness structure within the population. In tournament

selection, a certain number of chromosomes is randomly selected, depending on the

tournament size s. The best chromosome wins the tournament with probability p and

overcomes the selection phase. We favor a binary tournament selection. It picks two

individuals from a population of chromosomes and selects the better. Therefore a

chromosome’s fitness rank within a population is crucial rather than the value of its

fitness.

109

4.8 Crossover

Several crossover operators have been developed which enable a global exploration of

the search space. The results of the different crossover operators are very

heterogeneous. Therefore Whitfield et al. [29] compared several crossover strategies

for DSM sequencing. Due to the feasibility of a mapping a C3 model into a DSM the

results of Whitfield et al. give a conclusion about their performance regarding the

considered C3 modeled RCMPSP. A crossover procedure based on a version of one

point crossover is used that works as follows [23, 32]:

Step 1: Two chromosomes that passed the selection phase are chosen randomly from

the population (probability p

). One of them is randomly designated as the “primary”

parent (Parent 1). These two chromosomes Parent 1 and Parent 2 undergo crossover

according to the crossover probability p

Step 2: If these both chromosomes undergo crossover a position (locus) along both

parents is chosen by random. The position of Parent 1 corresponded with locus of

Parent 2.

Step 3: Select and place the genes of the first part of Parent 1 into the positions at the

beginning of Offspring 1. The second part of Parent 2 is set into the loci right of the

cutting position to complete Offspring 1. Due to the fixed assignment <locus, Task

ID> for all chromosomes of a generation the crossover operator only generates valid

solutions.

Step 4: The generation of the second offspring (Offspring 2) is taken place

analogously.

Figure 1 provides a graphical example of this process. The offspring first inherits

four genes from parent 1 at loci (1,2,3,4) and then the remaining genes from parent 2

at loci (5,6,7).

4.9 Mutation

Mutation is able to produce new chromosomes and can be helpful when the effects of

crossover diminish, diversity slowly disappears, and the GA begins to converge [31].

Due to empirical results of Whitfield [29] we favor a modification of a two operaton

swap [23]. A chromosome that passed the selection phase is chosen randomly from

the population for mutation (probability p

). Two genes (A

, A

) or a multiple of two

are then accidentally selected. The first gen at loci A

partly exchanges values (alleles)

with the gen of loci A

under consideration of predecessor and resource constraints. In

particular the assignment of actors and resources are swapped but also the starting

time of the activity (period relating to the ending time of the predecessor tasks),

stochastic value to determine makespan or the occurrence of iteration.

5 Computational Results

We now present test results for the GA and the Petri-Net simulation model. We

performed tests for C3 models with different project specific characteristics. The

110

results give a first impression of the performance of the GA. Further studies are

currently in progression.

5.1 Case Study

The performance of the developed GA is tested on a RCMPSP – three a posteriori

modeled development projects in an enterprise of the chemical engineering industry.

The projects for the development of three large scale chemical engineering plants

have respectively 62 different tasks with project specific characteristics. While the

projects are unrelated, the execution of the 186 tasks depends on the common pool of

actors and resources of the involved organization units as well as precedence

relationships of tasks within a project. But there exist no precedence relationships

between the three projects. Tasks durations range from 1 to 60 time units. Every

project is characterized by two iterations which are combined to a cascade. For the

real and complex development processes an ideal sequence and assignment of actors

is not known, and finding the global optimum may is difficult with respect to the

problem size and constraint.

5.2 C3 Related Results

We expected the population size and crossover rate to be a problem: the larger the

crossover rate and the population, the greater is the chance that the best individuals of

a generation are not continuously improved. As the population size increases, the best

fitness value for each population improves. Figure 2 provides us an insight into the

change of the best fitness value over population size and how crossover probability p

impacts the performance. When population size reaches the task string size (number

of tasks: 186), the optimal makespans become stable. These results are consistent with

the findings of Zhuang et al. [33]. For such kind of scheduling problem, a decent

solution is expected when population size is the number of genes. With large enough

population, the initialization ensures that good schemas appear. When crossover rate,

= 0.85, the GA generated much better fitness values than those at p

= 0.05. It

indicates that the implemented crossover operator dictate the evolution.

Fig. 2. Average fitness value versus population size.

111

It is demonstrated in Figure 3 that the fitness value increases as generation

increases. A fast convergence rate is shown for the crossover due to moderate

precedence relationships of tasks. It is observed from Figure 3 that the global

optimum for the fitness value does not appear until several generations. Due to the

multi criteria objectives the optimum of the project duration does not present the best

solution for the project costs or the capacity utilization.

Fig. 3. Fitness Value at population 50.

It is shown in Figure 4 the project duration and cost of the fittest and worst

individual of each generation.

Fig. 4. Project Duration and Cost.

In this section we will also relate the performance of the proposed GA to a Petri

net based simulation model for task scheduling [12]. A best solution for the RCMPSP

is given by our simulation model: 690 TU and 505 CU. It is observed that our GA is

capable of significantly reducing the project duration, compared to the simulated

project scenarios. The difference regarding the project costs was low due to the low

variance of the wage of different actors.

The proposed GA-based scheduling method has demonstrated its advantage over

the simulation approach in terms of simulation time, accuracy and efficiency in this

particular test case.

112

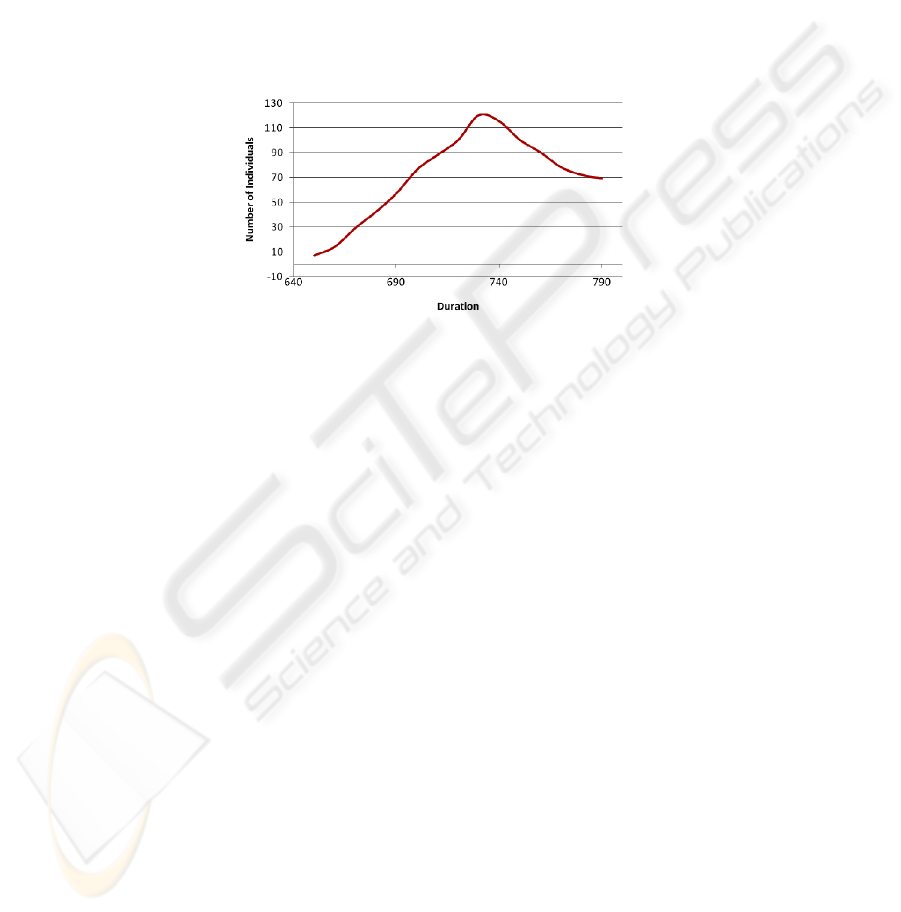
5.3 Stochastic Feedback

A project organization without any iterative execution of a task is often only a

baseline schedule. In reality, some downstream tasks may be forced to be repeated

due to changes in requirements of task`s outcome. In order to accommodate this

problem, this GA-based approach randomly generates a value based on the feedback

probability and thus decides whether the feedback will be part of schedule or not. The

model also considers that the probability of a feedback loop can be decrease or

sometimes increase during multiple executions of a loop. Also it was implemented

that the effort of a task during several iterations can vary. The value of the variance is

based on the knowledge of the project manager and is calculated with the equation

(4).

Fig. 5. Project Duration for projects with stochastic feedback.

Random trials with possible different feedback tasks of the three projects are

generated and an optimal schedule is obtained for each. A distribution function is

found to best fit the resulting project distribution as shown in Figure 5. It is helpful to

identify the most likely project duration range and provide a better understanding of

how long the project may last. As such, we can conduct a sensitivity test on the

project portfolio and evaluate how the three optimal project schedules are sensitive to

changes in feedback structure.

6 Concluding Remarks

This paper has proposed an implementation of Genetic Algorithms to solve a C3

model representation of the resource constrained multi-project scheduling problem for

multi-criteria objectives. A population was initialized due to simulation runs of a Petri

net model such that all individuals are precedence feasible. The novel characteristic of

a genotype for the RCMPSP and GP mapping was introduced to maintain precedence

and resource feasibility while obtaining the project duration, costs and degree of

capacity utilization for fitness evaluation. The development of a novel GP mapping

function was necessary due to the integration of uncertainties in the project model.

Good solutions were found however by using simple mutation and crossover

operators. These genetic operators perform well for the continuous improvement of

113

chromosomes over generations. It also accommodates feedback which is of

paramount importance in a management of several concurrent development projects.

A great focus of future work should be on the integration of human behavior in the

project model. This GA-based methodology can be easily extended to project models

that include cooperation, coordination and communication processes between actors.

In the latter case, preemption of tasks will be allowed. Therefore actors and resources

will be available whenever tasks of a higher priority are ready to be performed.

Finally, extensions to GA operators (crossover, mutation) to enlarge the performance

can be made as well as the multi-objective fitness function can be revised to find

better solutions for conflictive targets.

References

1. Bäck, T., 1994. Selective Pressure in Evolutionary Algorithms: A Characterization of

Selection Mechanisms. Proceedings of the First IEEE Conference on Evolutionary

Computation, Vol. 1, 57–62.

2. Brindle, A., 1981. Genetic Algorithms for Function Optimization. Doctoral dissertation,

University of Alberta, Edmonton, Canada.

3. Browning, T. R., and Eppinger, S. D., 2002. Modeling Impacts of Process Architecture on

Cost and Schedule Risk in Product Development. In: IEEE Trans. Eng. Manage., 49(4),

428–442.

4. Duckwitz, S., Licht, T., Schmitz, P., Schlick, C. M., 2008. Actor-Oriented, Person-

Centered Simulation of Product Development Projects. In: Bertelle, C.; Ayesh, A. (Ed.).

The 2008 European Simulation and Modelling Conference. Ghent, Belgien, EUROSIS-ETI,

66-73.

5. Garey, M. R., Johnson, D. S., 1979. Computers and intractability: A guide to the theory of

NP-completeness. W. H. Freeman & Co., New York

6. Ghomi, S., Ashjari, B, 2002. A simulation model for multi-project resource allocation. In:

International Journal of Project Management, 20(2), 127-130.

7. Goncalves, J.F., Mendes, J.J.M., Resende, M.G.C., 2008. A genetic algorithm for the

resource constrained multi-project scheduling problem. European Journal of Operations

Research, 189, 1171-1190.

8. Grünert, T., Irnich, S. 2005. Optimierung im Transport, Band 1: Grundlagen, 182-244.

Shaker Verlag GmbH, Aachen.

9. Hartmann, S., 1998. A competitive genetic algorithm for resource-constrained project

scheduling. Naval Research Logistics, 45, 733-750.

10. Hölltä-Otto, K., Magee, C. L., 2006. Estimating factors Affecting Project Task Size in

Product Development – An Empirical Study. IEEE Trans. Engineering Management, 53(1),

86-94.

11. Huberman, B.A., Wilkinson, D.M., 2005. Performance Variability and Project Dynamics.

Computational & Mathematical Organization Theory, 11(4), 307-332.

12. Kausch, B., Grandt, M., Schlick, C. 2007. Activity-based Optimization of Cooperative

Development Processes in Chemical Engineering. In: SCSC 2007 “Summer Computer

Simulation Conference”, 15-18 July 2007, San Diego.

13. Kelley, J.E. Jr., 1961. Critical-Path Planning and Scheduling: Mathematical Basis. In:

Operations Research, 9(3), 296-320.

14. KHosraviani, B., 2005. An Evolutionary Approach for Project Organization Design:

Producing Human Competitive Results Using Genetic Programming. Doctoral Dissertation,

Department of Civil and Environmental Engineering, Stanford

114

15. Kolisch, R., Padman, R., 2001. An integrated survey of project deterministic scheduling. In:

International Journal of Management Science, 29(3), 249–272.

16. Kolisch, R. (2000): Integrated scheduling, assembly area- and part-assignment for large-

scale, make-to-order assemblies. International Journal of Production Economies, 64, 127-

141.

17. Kolisch, R., Hartmann, S. 1998. Heuristic algorithms for solving the resource constrained

project scheduling problem: classification and computational analysis. In: Handbook on

Recent Advances in Project Scheduling, Kluwer, Boston.

18. Kummer, O., Wienberg, F., Duvigneau, M., 2006. Renew – the Reference Net Workshop.

appeared as electronic version ww.renew.de.

19. Lenstra, J., Rinnooy, K., 1978. Complexity of Scheduling under Precedence Constraints.

Operations Research, 26(1), 22-35.

20. Liepins, G.E., Vose, M.D. 1990. Representational issues in genetic optimization. In:

Journal of Experimental and Theoretical Artificial Intelligence, 2(2), 4-30.

21. Linyi, D.; Yan, L., 2007. A Particle Swarm Optimization for Resource-Constrained Multi-

Project Scheduling Problem. International Conference on Computational Intelligence and

Security, doi:10.1109/CIS.2007.157.

22. Malcolm, D.G., 1959. Application of a Technique for Research and Development Program

Evaluation. In: Operations Research, 7(5), 646-669.

23. Murata, T., Ishibuchi, H., 1994. Performance Evaluation of Genetic Algorithms for Flow

Shop Scheduling Problems. In: Proceedings of the First IEEE Conference on Genetic

Algorithms and their Applications Orlando, FL, June 27–29, 812–817.

24. Nonobe, K., Ibaraki, T., 2001. A Local Search Approach to the Resource Constrained

Project Scheduling Problem to Minimize Convex Costs. 4th Metaheuristics International

Conference, Porto, Portugal.

25. Schlick, C. M., Beutner, E., Duckwitz, S., Licht, T., 2007. A Complexity Measure for New

Product Development Projects. In: Proceedings of the 19th International Engineering

Management Conference, IEMC 2007, Managing Creativity: The Rise of the Creative

Class. Austin, Texas, USA, 143-150.

26. Shouman, M.A.; Ibrahim, M.S.; Khater, M.; Forgani, A.A., 2006. Genetic algorithm

constraint project scheduling. Alexandria Engineering Journal, Vol. 45, No. 3, 289-298.

27. Tackenberg, S., Kausch, B., Malabakan, A., Schlick, C. M., 2008. Organizational

Simulation of Complex Process Engineering Projects in the Chemical Industry. In:

Proceedings of the 2008 12th International Conference on Computer Supported

Cooperative Work in Design Vol. II, April 16-18, 2008 Xi'an, China, IEEE Press, Beijing,

648-653.

28. Thierens, D., 1995. Mixing in genetic algorithms. Doctoral Dissertation, Katholieke

Universiteit Leuven

29. Whitfield, R. I., Duffy, A. H. B., Coates, G., Hills, W., 2003. Efficient Process

Optimization, Concurr. Eng. Res. Appl., 11(12), 83–92.

30. Yang, B., Geunes, J., O’Brien, W.J., 2001. Resource-Constrained Project Scheduling: Past

Work and New Directions. Research Report 2001-6, Department of Industrial and Sys.

Engineering, University of Florida.

31. Yassine, A. A., Meier, C., Browning, T. R. 2007a. Design Process Sequencing With

Competent Genetic Algorithms. Transaction of the ASME, 129, 566-585.

32. Yassine, A. A., Meier, C., Browning, T. R. 2007b. Multi-Project Scheduling using

Competent Genetic Algorithms. Working Paper, University of Illinois

33. Zhuang, M., Yassine, A. A., 2004. Task Scheduling of Parallel Development Projects

Using Genetic Algorithms. In: Proceedings of DETC `04 ASME 2004, International Design

Engineering Technical Conferences and Computers and Information in Engineering

Conference. Salt Lake City, Utah, USA, 143-150

115