PARAMETERIZATION OF SAMPLES FOR MODELING OF

LASER BURNING

Increasing the Lifelikeness of Synthetically Generated Samples

Jana Hájková and Pavel Herout

Department of Computer Science and Engineering, University of West Bohemia, Univerzitní 8, Pilsen, Czech Republic

Keywords: Parameterization, Sample Generation, Pulse Approximation, Roughness, Laser Simulation, Concentric

Waves, Perlin Noise Function, Distortion.

Abstract: This paper describes methods for the generation of samples in modeling burning by a laser beam. In the first

part, it briefly informs about real data set and the way of approximation of real samples by mathematically

described smooth surfaces. In the main part, the paper focuses on methods which can be used for increasing

the lifelikeness of the result of the sample generation process for simulation purposes. Finally, the results

are summarized and the future plans are outlined.

1 INTRODUCTION

The work described in this paper is a part of a larger

project that deals with laser burning control and

simulation of laser burning process. We are

interested in processing the measured data, its

visualization and laser burning simulation. For our

work, we use real samples burned by a laser and

measured by a confocal microscope. The means of

data acquisition process is described in (Hájková,

2008).

All measured samples are represented in the

form of a height map. As a part of data processing,

we are going to find a set of parameters that would

define a mathematical function approximating the

shape of the pulse optimally and to get a

parametrical description of the sample roughness in

all its areas. The parametrical description could be

used as a part of the sample simulation process.

First, we generate the basic shape of the pulse. Than,

to get more realistic results, the basic smooth surface

can be further adjusted by using methods for a

random surface modification described in this paper.

1.1 Data Description

As mentioned in the introduction, the description of

each measured real sample is stored in the format of

a height map. This height map is formed by a matrix

of real numbers, which express the heights of

intersection points in a uniform rectangular grid. The

whole data set consists of samples with a defined

number of laser beam pulses burned by a laser into a

single point in the material.

To get a better imagination about the appearance of

a sample, see

Figure 1, where an example of a sample cross-

section is shown. It contains several typical features,

which result from the burning process and the

character of used material.

Figure 1: A typical cross-section of a sample.

During the burning process, the surface of the

material is exposed to an intense pulsed laser beam

that causes a rapid rise in local temperature. The

surface is warming up and the material starts to

ablate. The material, which is ablated, redeposites

around the irradiated area and damages the

surrounding material (Dahotre et al., 2008). Finally,

at the exposure site, a pit with a transition ring

around it is left behind. An example sample (100

283

ajkov

a J. and Herout P. (2009).

PARAMETERIZATION OF SAMPLES FOR MODELING OF LASER BURNING - Increasing the Lifelikeness of Synthetically Generated Samples.

In Proceedings of the 4th International Conference on Software and Data Technologies, pages 283-286

 SciTePress

laser pulses burned into a single point in steel) in 3D

view can be seen in Figure 3a.

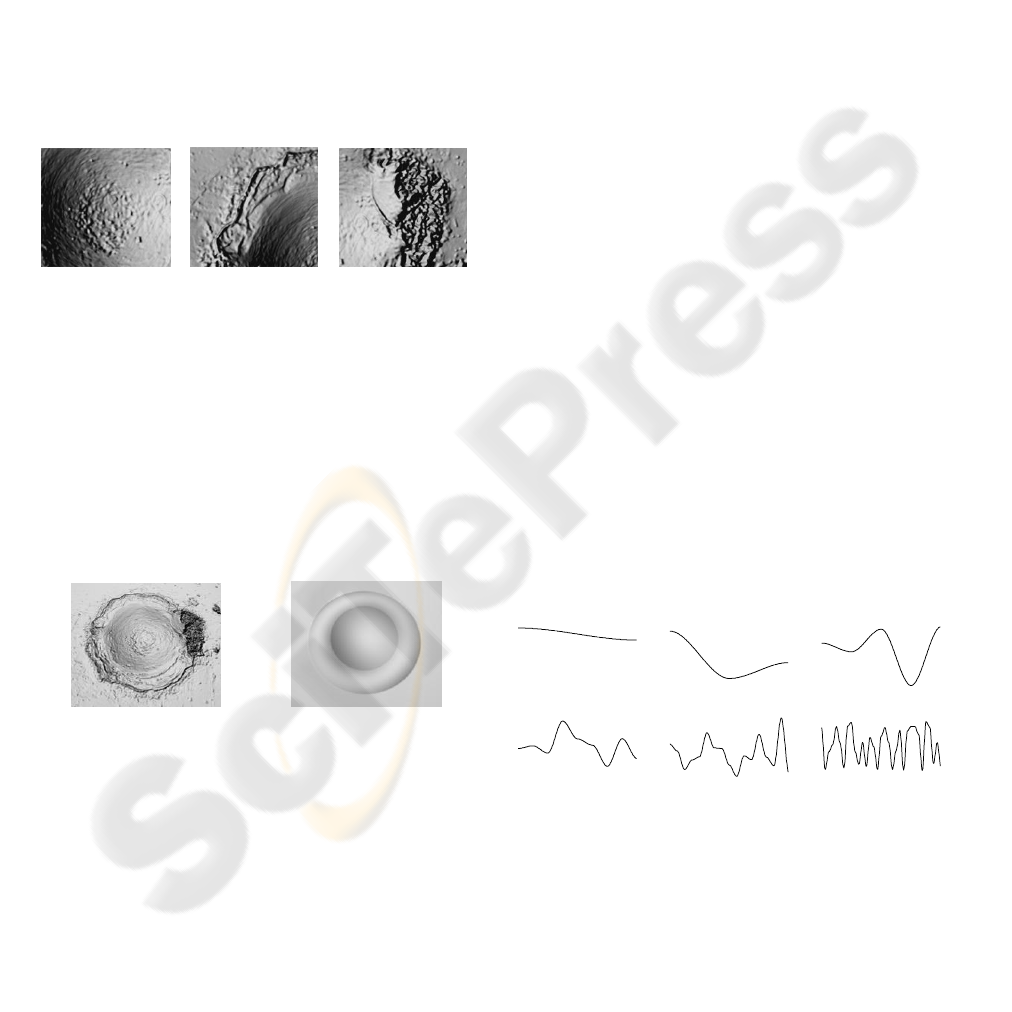
The central part of the pulse (i.e., the area

directly irradiated by the laser beam) is smooth and

the bottom of the pit is a little bit rougher (Figure

2a). The most ragged surface part is the transition

ring. The surface is modulated by some concentric

waves that are both regular and irregular (Figure 2b).

Sometimes, local defects with a considerable

roughness can appear, especially at the outer border

of the transition ring (Figure 2c). At the outer

border, the roughness declines slowly and fades into

the roughness of the bulk material. All these facts

should be taken into account if we want to generate

a realistically looking surface of a laser-burned

sample.

a) b) c)

Figure 2: Examples from different parts of a typical

sample surface.

1.2 Sample Shape Approximation

As described in (Hájková, 2009), the basic shape of

a sample can be approximated by a smooth surface

defined by mathematical functions which

approximate the pulse pit by an elliptical paraboloid,

and the pulse transition ring by the top half of a

parabolic elliptic torus. An example of a real sample

and its approximation can be seen in Figure 3.

a) b)

Figure 3: An example of the sample approximation by a

smooth surface.

To obtain the most realistically looking sample,

surface the generated surface should be further

modified and some roughness should be added.

2 ROUGHNESS GENERATION

If we burn the same sample twice into different

places, it will never be the same, because at least the

surface of the basic material differs. That is why we

have to enhance the sample generation with random

features such as noise or various defects to get more

realistic results. These features and the methods how

to generate them are described in the following

subsections.

2.1 Perlin Noise Function

As can be seen in Figure 3, the mathematically

generated sample is too smooth in comparison with

the real one. That is why it is necessary to modify a

generated surface by some kind of artificial defects

that would represent the granularity of the material

and the roughness of different parts of a real sample.

One of the possible solutions is to use the Perlin

noise function (Perlin 1985), (Perlin, 2002). The

Perlin noise function has a very wide range of

application, not only in the computer graphics, but

also in many other areas, where natural appearance

is required.

Perlin noise combines a noise function with an

interpolation function. The noise is formed by

randomly generated values the distance of which is

given by some frequency. This frequency is defined

as 1/wavelength, where the wavelength represents

the distance from one generated value to the next

one. The generated values are interpolated using the

Hermit interpolation (Žára et al., 2005) to get a

smooth interpolating curve (with given amplitude

and frequency). If we sum up several curves (called

octaves) with various frequencies and amplitudes,

we get the final Perlin noise function. An example of

1D octaves can be seen in Figure 4. The frequency

ranges from 1 to 32, the amplitude is the same for all

octaves.

Figure 4: Octaves that are added to the final 1D Perlin

noise with the same amplitude and different frequencies:

a) 1, b) 2, c) 4, d) 8, e) 16, f) 32.

For the modification of the generated smooth

material surface, we need the 2D Perlin noise. A

different number of octaves can be added into the

final 2D noise or various amplitudes can be used.

Several examples of the final 2D Perlin noise are

shown in Figure 5.

ICSOFT 2009 - 4th International Conference on Software and Data Technologies

284

Figure 5: 2D Perlin noise after summing up 6 noise

functions with different amplitudes. Amplitude of each

following octave is a) the same; b) half; c) quarter the size.

d-f) Perlin noise generated according to three different

amplitude vectors.

It is evident that the variability of the Perlin

noise function is high and so we can use it for the

realistically appearing samples generating.

Perlin noise can be used several times during the

process of pulse generation. The result depends on

the used parameters. The first case, where the Perlin

noise can be used, is the generation of the roughness

of the pit bottom. The roughness is generated

according to the noise amplitude vector. A real

sample (100 laser pulses burned into steel) is shown

in Figure 6a, an example of the Perlin noise

modulated surface of the ideal pit can be seen in

Figure 6b.

a) b)

Figure 6: a) The pit of a real sample; b) Perlin noise

modulated on the surface of the ideal pit.

Another area where the usage of the Perlin noise

is appropriate is generating the transition ring, or to

be more precise, some local defects on it. To get a

better imagination how the generated surface looks

like, compare the 3D surface of the real local defects

in two samples in Figure 7a,b and the surface

generated by the Perlin noise in Figure 7c.

For the sample generation, we need to form

several smaller areas representing the local defects.

For this purpose we can also use the Perlin noise. At

the beginning, we generate a mask of the transition

ring (see Figure 8a). Then, we generate another

mask representing the basic shape of the thresholded

Perlin noise (Figure 8b). If we make an intersection

of both masks, we get the result mask shown in

Figure 8c. This result mask serves for the

modulation of the Perlin noise described above

(Figure 8d). To get a more realistic appearance, the

original shape of the transition ring mask could be

slightly changed by a distortion.

a) b) c)

Figure 7: a, b) Local defects in two different samples;

c) surface generated by the Perlin noise.

a) b)

c) d)

Figure 8: a) Mask of the transition ring; b) mask of the

local defect areas; c) intersection of both previous masks;

d) final result after the generation of local defects.

2.2 Waves Modulation

In the real samples, concentric waves are visible in

the area of the transition ring (as shown in Figure

2b). These waves are especially noticeable on the

outer border of the ring, they are relatively thin and

sometimes even discontinuous. Their shape consists

of a number of edges which approximately form an

elliptical shape.

If we want to generate a wave, we have to know

several parameters for its description, e.g. its

diameter, width, height or segmentation. The

segmentation is determined with the set of points

forming a line segment. All line segments are

converted to an arc plane with the given width and

height.

In the real samples more than one wave can often

be recognized. Examples of 20 and 30 waves

modulated on the smooth sample surface can be seen

in Figure 9.

PARAMETERIZATION OF SAMPLES FOR MODELING OF LASER BURNING - Increasing the Lifelikeness of

Synthetically Generated Samples

285

a) b)

Figure 9: Examples of a) 20 and b) 30 waves modulated

on the smooth sample surface.

3 RESULTS

If we put all the generated parts together, we obtain

the final sample. For the basic material, the surface

of the measured real sample is used. Than, the basic

shape of the pit is computed and its bottom is

modified by the Perlin noise. After that, we can

generate the transition ring. Its basic shape is

computed, the masks for the ring and the Perlin

noise are created and then used for its modification.

Results can be seen in Figure 10. The original

samples with 10, 50, and 100 laser pulses burned

into steel are shown are placed in the left column.

They can be compared with the results of the pulse

generation, which are placed in the right column.

Figure 10: Real and generated samples: a) 10; b) 50;

c) 100 laser pulses burned into a single point in steel.

4 CONCLUSIONS

This paper describes methods for the roughness and

noise generation. They serve for increasing the

lifelikeness of samples which are synthetically

generated based on the parameters gained from the

real measured data. This can be used as a basic

approach for the laser burning process simulation.

The set of parameters consists of the parameters

describing the pulse basic shape (such as its inner

and outer border diameters, its depth or the maximal

height of the transition ring) and of several

parameters for the roughness description (such as

amplitude vectors for the Perlin noise, waves

parameters, etc.).

The majority of parameters have to be obtained

automatically to ensure the self-contained data

processing. Some parameters depend on the used

material and the others are typical for a particular

number of laser pulses burned into a single point. As

can be seen in Figure 10, the present results look

very well and the improvement of the generating

process automation is one of the tasks we want to

work on in the future.

ACKNOWLEDGEMENTS

This work was supported by the Ministry of

Education, Youth and Sport of the Czech Republic

“University specific research – 1311”.

REFERENCES

Dahotre, N. B., Harimkar, S. P. 2008. Laser Fabrication

and Machining of Materials, Springer, New York,

USA.

Hájková, J., 2008. Methods of Pulse Detection in Laser

Simulation, Proceedings of the 3rd International

Conference on Software and Data Technologies

ICSOFT 2008, ISBN: 978-989-8111-57-9, pp 186-

191, Porto, Portugal.

Hájková, J., 2009. Parameterization of Laser Burned

Samples and its Usage in Data Description and

Simulation, in preparation. accepted to 23

European

Conference on Modeling and Simulation ECMS2009,

Madrid, Spain, 2009.

Perlin, K. 1985. An Image Synthetizer, Proceedings of the

12th annual conference on Computer graphics and

interactive techniques, ISBN: 0-89791-166-0. ACM

New York, USA, pp. 287-296.

Perlin, K. 2002. Improving noise, Proceedings of the 29th

annual conference on Computer graphics and

interactive techniques, ISBN: 0730-0301. ACM New

York, USA, pp. 681-682.

Žára, J., Beneš B., Felkl P. 2005. Moderní počítačová

grafika, ISBN 80-251-0454-0. Computer Press, Brno,

Czech Republic.

ICSOFT 2009 - 4th International Conference on Software and Data Technologies

286