MONITORING NODE SELECTION ALGORITHM FOR

INTRUSION DETECTION IN CONGESTED SENSOR NETWORK

Jaeun Choi, Myungjong Lee, Gisung Kim and Sehun Kim

Dept. of Industrial & System Engineering, Korea Advanced Institute of Science and Technology, 335 Gwahangno

Yuseong-gu, Daejeon 305-701, Republic of Korea

Keywords: Intrusion detection, Congestion control, Wireless sensor network, Reliable sensor network.

Abstract: Since wireless resources are limited, an efficient way of utilizing wireless resources is needed in selecting

IDSs. We propose a monitoring node selection scheme for intrusion detection in congested wireless sensor

network. Network congestion is an important issue in mobile network. The network congestion does not

guarantee a proper detection rate and congested networks should cause an unreliable network. We consider

congested intrusion detection tasks by queuing theory. We confirm that proposed algorithm guarantee QoS

of monitoring tasks and reliable sensor networks.

1 INTRODUCTION

In recent years, as wireless network techniques

develop rapidly, security becomes one of the major

problems in wireless network. Wireless networks are

notably vulnerable to intrusions, as they operate in

open medium and don’t have any centralized

security systems. In contrast to wired networks,

wireless networks need a special method to detect

intrusions.

An Intrusion Detection System (IDS) for

wireless networks is widely employed for security

purpose to detect illegal intrusions. An IDS is a

system that tries to detect intrusions in the network

using statistical behavior models. To detect

intrusions, all nodes should be monitored by IDS

nodes. Only considering security, every node had

better perform intrusion detection. However, this

approach is inefficient in terms of wireless resources

such as network bandwidth and node battery. If all

nodes implement intrusion detection processing, the

wireless resources are inefficiently used and some

nodes are suffered from battery depletion, because a

node acting as an IDS which overhears and analyses

all packets within monitoring range consumes

additional resources. Since wireless network

resources such as battery and bandwidth are limited,

an efficient way of utilizing these wireless resources

is needed in construction IDSs (Kachirski O. and

Guha R., 1999), (Kim H. et al., 2006).

In this paper, we apply an IDS node selection

scheme to a wireless sensor network (WSN). A

wireless sensor network is a wireless network

consisting of distributed sensors to cooperatively

monitor physical or environmental conditions, such

as temperature, sound, vibration, pressure, motion or

pollutants, at different locations (Römer, Kay;

Friedemann Mattern, 2004), (Thomas Haenselmann,

2006). Wireless sensor networks are now used in

many industrial and civilian application areas

(Römer, Kay; Friedemann Mattern, 2004), (Hadim,

Salem; Nader Mohamed, 2006). Wireless sensor

networks have constraints on resources such as

energy, memory, computational speed and

bandwidth (Römer, Kay; Friedemann Mattern, 2004).

Therefore, an efficient IDS selection algorithm is

required in wireless sensor network.

There are two related works to select monitoring

nodes for intrusion detection before, distributed IDS

(DIDS) and lifetime-enhancing monitoring node

selection (LES) (Kachirski O. and Guha R., 1999),

(Kim H. et al., 2006). These schemes efficiently use

wireless resources such as network lifetime or

battery consumption of whole network. However,

previous researches did not consider congestion of

monitored packets in a buffer of IDS. Our work

differs from others by considering congestion of

monitoring tasks. In recent years, data transmission

speed becomes faster and faster. If the data

transmission rate is faster than monitoring rate, the

unmonitored packets increase in a buffer of IDS.

117

Choi J., Lee M., Kim G. and Kim S. (2009).

MONITORING NODE SELECTION ALGORITHM FOR INTRUSION DETECTION IN CONGESTED SENSOR NETWORK.

In Proceedings of the International Conference on Security and Cryptography, pages 117-120

DOI: 10.5220/0002225001170120

 SciTePress

When congestion occurs in a node due to high

packet arrival rates, the IDS cannot afford to monitor

the all arrival packets and the buffer overflow

happens. So the IDS becomes ineffective and

deteriorated. Hence, it is desirable to assign IDS

node to the network properly so that prevent the

denial of IDS service due to the overflow.

In this paper, we propose a monitoring node

selection algorithm for intrusion detection in

congested sensor network. By using queuing theory,

we prevent congested monitoring situations. In

congested system, our proposed scheme has the

longest network lifetime and the smallest total

battery consumption than other existing schemes. By

preventing congested monitoring tasks, our

algorithm guarantees QoS of monitoring tasks and

reliable sensor networks.

2 ALGORITHM

We propose an IDS node selection scheme based on

two requirements. First, to monitor all nodes in the

network, every node should be in the monitoring

coverage of IDS. Second, to prevent the congestion

of monitored packets, we design the IDS nodes

placement scheme considering congested systems.

For satisfying the first requirement, we apply a set

covering problem (SCP) to the IDS nodes selection

scheme.

The SCP is a classical question in computer

science and complexity theory. The SCP selects a

minimum number of sets that contain all elements

and additionally minimizes the cost of the sets.

Therefore, the SCP guarantees that every element is

covered by at least one server at minimal total cost.

To cover all nodes by minimal IDS, we propose a

formulation using the SCP. The formulation of the

IDS node placement scheme using the SCP is as

follows;

min

{0,1}

ij j

taxiN

≥ ∀ ∈

∈ ∀ ∈

∑

(1)

Formulation (1) is a typical SCP formulation.

Binary variable x

is one if node j is IDS node, and

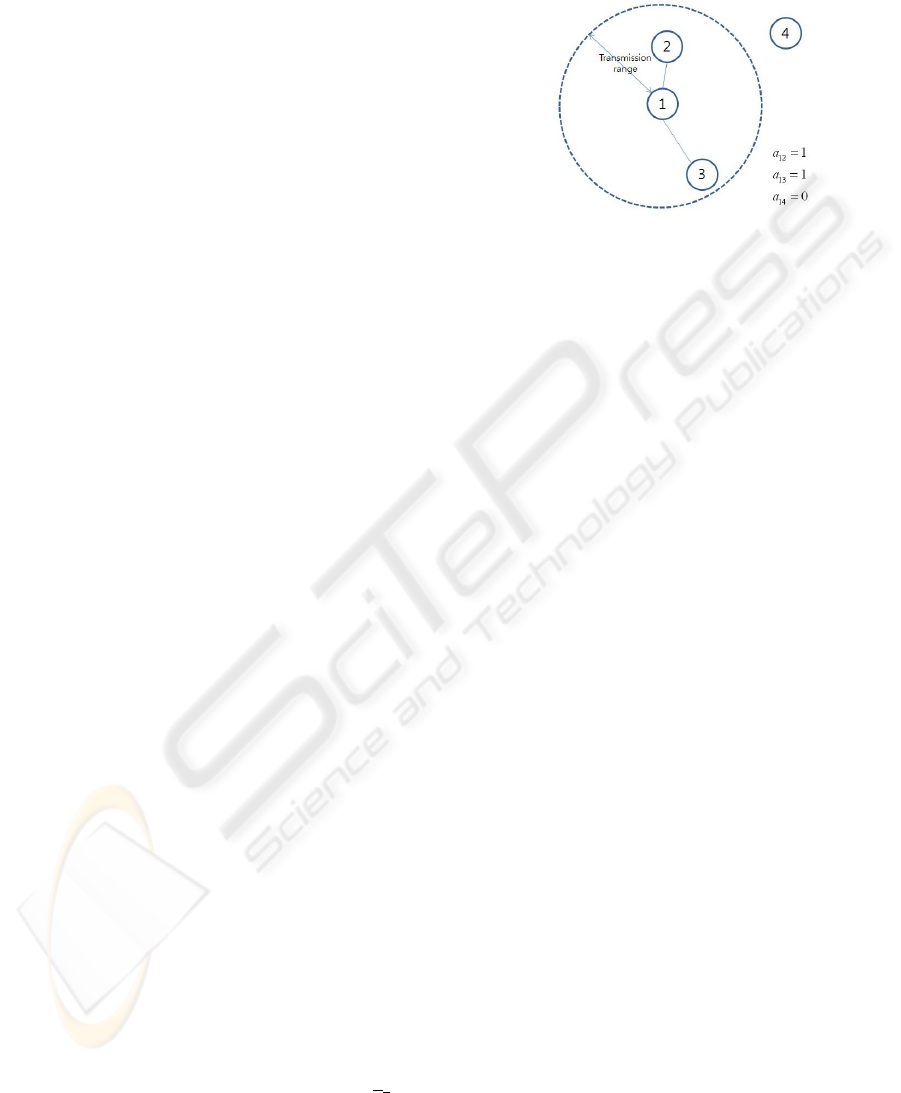
zero otherwise. Like figure 1, binary variable a

one if node j is in the transmission range of node i,

and zero otherwise. In the typical SCP, c

is the cost

which is needed to select server j. In this problem,

every node has same weight. Therefore, we define c

of every node as 1. We define the set N as the set of

all nodes in the network.

Figure 1: Transmission range of a wireless node.

Formulation (1) satisfies the first requirement.

Then, we discuss a constraint considering congested

systems. An implicit assumption in traditional SCP

is that each node in the coverage of a server always

receive satisfied service. However, when a server

suffers from congestion by excessive demand, some

users are not able to receive satisfied service in the

real situation. Especially, if an IDS node suffers

from congestion of monitored packets, intrusion

detection efficiency is reduced and battery

consumption of the IDS is high. In order to

guarantee high detection rate and use efficiently

limited wireless resources, considering congested

systems is important. To prevent congestions, any

packet should not stand in waiting line in the buffer

of IDS nodes for a time longer than a given time-

limit (Marianov, V. and Serra, D., 1998). The

constraint which considers congestion is as follows;

[]P waiting time at IDS node j j

≤ ≥ ∀

(2)

Constraint (2) makes the total time spent by a

packet at the IDS node shorter than equal to τ with

probability of at least α. The variables τ and α are

predefined time and probability. In order to express

constraint (2) as a numerical formula, we use the

queuing theory (Marianov, V. and Serra, D., 1998).

In this paper, we make an assumption that an packet

arrival rate from node i to j appears according to a

poisson process with intensity f

. Also, we assume

an exponentially distributed monitoring service time,

with an average rate of μ

. This is a reasonable

assumption, since IDS systems behave as M/M/1

queuing systems. As we assume a M/M/1 queuing

system, we are able to use the well known results for

a M/M/1 queuing system for each IDS and its

allocated nodes (Marianov, V. and Serra, D., 1998).

Rewriting constraint (2) as a numerical formula, we

get

SECRYPT 2009 - International Conference on Security and Cryptography

118

ln (1 )

ij ij j j

ax j N

μα

≤ + − ∀ ∈

∑

(3)

Adding constraint (3) to formulation (1), we

finally get our proposed formulation as follows;

min

,ln(1)

{0,1}

ij j

ij ij j j

st a x i N

fax D

where D j N

xjN

μα

≥ ∀ ∈

≤

= + − ∀ ∈

∈ ∀ ∈

∑

(4)

3 PERFORMANCE MEASURE

The normal node uses their energy for transmission

and receiving. Additionally, the monitoring node

overhears packets within monitoring range, and

analyzes them to detect intrusions. The battery

consumed by a monitoring node is calculated as:

()( )( )( )

tt t rr r oo o mm m

ms b ms b ms b m s b=++ ++ ++ +

(5)

where, s

, s

and s

, respectively, represent the

packet sizes for operations : transmission, receiving,

overhearing and monitoring. Factors m and b are

variable and fixed energy costs for each operation

(Feeney LM, Nilsson M. 2001). We will show

numerical simulations using equation (5).

For comparison with other schemes, we analysis

two performance measures; network lifetime and

sum of remain battery. The network lifetime defined

as the duration of time until the first node runs out of

battery. The network time is a meaningful

performance measure in a sense that a node which

has no battery cannot communicate with any other

nodes and it causes unreliable network (Kachirski O.

and Guha R., 1999). The sum of remaining battery

indicates total battery consumption of whole

network. By analysing this measure, we should

know efficiency of utilizing wireless resources

4 SIMULATION RESULTS

In the simulation, we consider a congested wireless

sensor network consisting of 20 nodes by

MATLAB. For the purpose of comparison, we

consider DIDS and LES mentioned above. We

generate certain amount of packets destined for

random nodes with a packet size of 512 bytes. Also,

we assume that all nodes have the same initial

battery. The simulation results are the average of

100 trials.

Figure 2: Network lifetime.

Figure 3: Sum of remain battery.

Figure 2 shows the average network lifetime in

congested systems and figure 3 shows the sum of

remain battery in congested network. In figure 2, the

network lifetime of proposed scheme is longer than

or similar to those of LES and DIDS. The total

battery consumption in proposed scheme is the

lowest among three schemes. By experiments,

proposed scheme has superior performance than

other existing schemes in congested network.

5 CONCLUSIONS

In this paper, we propose an IDS selection algorithm

for intrusion detection in congested sensor network.

In order to detect intrusions, the packets be buffered

in the queue of a monitoring node. If the buffer is

MONITORING NODE SELECTION ALGORITHM FOR INTRUSION DETECTION IN CONGESTED SENSOR

NETWORK

119

full, intrusion detection is not possible and it causes

the decline of detection rate. It means that congested

network cannot guarantee QoS of intrusion detection.

Moreover, the IDS node which is suffered from

congestion consumes more battery than other normal

IDS nodes.

To prevent congested IDS node, we use queuing

theory in set covering problem. Proposed algorithm

does not select IDS node which is suffered from

congestion of monitoring tasks. By experiment, in

congested situation, our proposed scheme has

superior performance than other existing schemes.

Moreover, we confirm that proposed algorithm

guarantee QoS of monitoring tasks and reliable

sensor network.

In the future works, the verification of our

algorithm is still required to use in the real situation.

Moreover, to reduce calculation time, heuristic

algorithms are required.

ACKNOWLEDGEMENTS

“This research was supported by the Ministry of

Knowledge Economy, Korea, under the

ITRC(Information Technology Research Center)

support program supervised by the IITA(Institute of

Information Technology Advancement)” (IITA-

2009-(C1090-0902-0016)).

REFERENCES

Kachirski O. and Guha R., 1999. Effective Intrusion

Detection Using Multiple Sensors in Wireless Ad Hoc

Networks, Proceeding of the international conference

on system sciences, Hawaii, 2003. p.57-64

Kim H., Kim D. and Kim S., Lifetime-enhancing selection

of monitoring nodes for intrusion detection in mobile

ad hoc networks, International Journal of Electronics

and Communications, (AEU) 60, 2006, p.248-250.

Römer, Kay; Friedemann Mattern, The Design Space of

Wireless Sensor Networks, IEEE Wireless

Communications 11 (6), December 2004, p. 54–61

Thomas Haenselmann, Sensornetworks, GFDL Wireless

Sensor Network textbook, 2006

Hadim, Salem; Nader Mohamed, Middleware Challenges

and Approaches for Wireless Sensor Networks, IEEE

Distributed Systems Online 7 (3), 2006

Marianov, V. and Serra, D., Probabilistic Maximal

Covering Location-Allocation Models for Congested

Systems, Journal of Regional Science 38, 1998, p.401-

424

Feeney LM, Nilsson M. Investigating the energy

consumption of a wireless network interface in an ad

hoc networking environment, Proceedings of

INFOCOM, Anchorage, 2001, p.1549-1557

SECRYPT 2009 - International Conference on Security and Cryptography

120