AN ALTERNATIVE APPROACH FOR FORMULA MODELLING IN
SECURITY METRICS
Rodrigo Sanches Miani, Felipe Marques Pires and Leonardo de Souza Mendes
Department of Communication, School of Electrical and Computer Engineering, State University of Campinas
Av. Albert Einstein, 400, Cidade Universitria ”Zeferino Vaz”, Distrito Baro Geraldo, Campinas, SP, Brazil
Keywords:
Security metrics, Network security, Security analysis.
Abstract:
This paper proposes an alternative approach to modelling the formula attribute within the context of security
metrics. This approach seeks to correct past errors by treating a security metric like a set, and inserting a
component that addresses the set intersection between the security elements. The work consists in to define
the model, explain the differences to the previous model and validate it, with examples from the metrics found
in literature and also with the results of a case study applied in Metropolitan Broadband Access Network in
Pedreira, a city located in the state of So Paulo, Brazil.
1 INTRODUCTION
A widely used concept in the information security
scope, is the security metric. Metrics can be defined
as a set of measures that can generate a quantitative
approach about a problem. (Lowans, 2002).
The primary goal of a metric is to convert raw
data into information capable of analysis. In the
information security world, large organizations as
CERT (Computer Emergency Response Team), SANS
(SysAdmin, Audit, Network, Security) and NIST (Na-
tional Institute of Standards and Technology) develop
and recommend the implementation of security met-
rics.
The metrics are usually defined from a series of
attributes. Among them we highlight: purpose, fre-
quency, data source, measures and formula. The for-
mula attribute, in particular, is important to describe
the calculations that will be performed to quantify the
metrics in a numerical expression (Swanson et al.,
2003). From the result of the formula, the metrics
value or indicator is obtained, and it is usually ex-
pressed in percentage terms.
This paper will present an alternative approach
that was proposed in (Miani et al., 2008) for the
modelling of security metrics formulas, aiming to in-
crease the reliability degree from the results obtained
by the formulas. We will show the differences be-
tween the two approaches and a comparative study of
the research results of a case study performed in the
Metropolitan Broadband Access Network of Pedreira.
This paper is organized as follows. Section 2
brings some related works of security metrics. The
section 3 presents the mainly motivations and defines
the concepts that will be studied in this work. In sec-
tion 4 we will introduce the basis of the proposed
model and the differences between the model that will
be compared. In section 5 we present one model ap-
plication example and the results of a metrics imple-
mentation case study developed in the Metropolitan
Broadband Access Network of Pedreira. The section
6 brings the conclusion and some future works.
2 RELATED WORKS
The study of security metrics and their applications
in the IT scenarios are targets of several discussions
(Rosenblatt, 2008). An increase in failure rate of
components, discovered vulnerability in software and
communication network attacks may cause a big con-
cern on questions related to information security. To
deal with these problems it is necessary to invest in se-
curity controls implementation and security policies.
The characteristics of these investments must be care-
fully accounted for and can be defined from measures
and analysis of information security structure. This
process is formalized using a security metrics appli-
cation (Weiss et al., 2005). Through a combination
381
Marques Pires F., de Sousa Mendes L. and Sanches Miani R. (2009).
AN ALTERNATIVE APPROACH FOR FORMULA MODELLING IN SECURITY METRICS.
In Proceedings of the International Conference on Security and Cryptography, pages 381-386
DOI: 10.5220/0002227303810386
Copyright
c
 SciTePress

of predefined objectives, collection and data analysis,
metrics can indicate the actual level of security we
must aim at, directing the actions network adminis-
trators must take to secure the network (Payne, 2006).
Jaquith (Jaquith, 2007), Swanson et al. (Swanson
et al., 2003), Payne (Payne, 2006) and the ISO/IEC
27002 (ISO, 2005) standard, contributed to the devel-
opment and formalization of attributes that constitute
a security metric.
Herrera (Herrera, 2005) examined the indicators
development from the security metrics, affirming that
there is no magical formula to establish the perfect in-
dicator, each organization shall determine which indi-
cators are useful according to their business and how
to get to the results. However, the growth and the need
for security metrics has created a gap in the concepts
standardization. Every security framework provides
its own security indicator method and this fact may
affect the development of security indicators.
The CVSS (Common Vulnerability Scoring Sys-
tem) (Mell et al., 2007) is an initiative in this direc-
tion. Its goal is the creation of standard indicators for
security vulnerabilities from the equations that are di-
vided in three groups of measures: base, temporal and
environmental. Popular vulnerability scanners such
as Nessus, already use the CVSS in their database, as
well as the NVD - National Vulnerability Database of
the U.S. government, maintained by NIST.
Other efforts in the standardization of measures in
the information security area can be found in (Jelen
and Williams, 1998). In this work, Jelen and Wil-
ians argue that assurance is an integral part of the risk
and security management process. They proposes a
formulation intended to be universal in the measuring
assurance area. Weiss et al. (Weiss et al., 2005) pro-
poses a model for the security level calculation of an
organization through the percentage of lost assets.
Miani et al. (Miani et al., 2008) defines a model
for formula calculation of security metrics. The at-
tributes that constitute the model are: objective, met-
ric, measure, data source, frequency, metrics clas-
sification and formula. The model standardizes the
nomenclature of terms relative to security metrics,
and proposes the formula calculation in a generic way
contributing to the decreasing of subjective criteria in
the metrics formulation. The model define the cal-
culation only using the arithmetic mean. This work
proposes a model that using set theory and the inclu-
sion of a new component, the intersection component,
that seeks to correct possible flaws in the model inter-
pretation proposed by Miani et al.
3 METRICS FORMULATION
The security metrics model, proposed in (Miani et al.,
2008) has a different characteristic from the tradi-
tional approaches, that is from the grouping of multi-
ple metrics in a common group, calculate the security
indicator of this group. For example, consider the fol-
lowing security metrics proposed by ISO/IEC 27002:
• P
1
= Percentage of communication channels con-
trolled by the organization that have been secured
in accordance with policy.
• P
2
= Percentage of mobile users who access
enterprise facilities using secure communication
methods.
• P
3
= Percentage of workstation firewalls, host
firewalls, sub-network firewalls, and perimeter
firewalls configured in accordance with policy.
Although the metrics are organized into a com-
mon group called “ Network access control”, they are
individually treated. Each metric has its own formula
and there are no recommendations on how to analyze
the whole group. The model proposed by Miani et
al. consists in, to combine the three metrics in only
one, aiming the overall group analysis by calculating
a single formula representing the “ Network access
control” level.
The grouping is important because it unifies sev-
eral results in only one number, easing the results
interpretation of the non-technical organization staff.
When necessary the calculation of individual metrics
can also be performed.
In this case, even according to the proposal, the
formula of the group “Network access control” it
would be calculated as follows:
Consider the components, P
1
, P
2
and P
3
. The next
step is to examine the component security. P
1
is se-
cure, because when the number of secure communica-
tion channels increase, the risks of security problems
decrease. Analogously, P
2
and P
3
are secure compo-
nents too. Thus, the formula is given by the arithmetic
mean between P
1
, P
2
e P
3
.
The simplicity and possible flaws in the interpre-
tation of results, are the main motivating factors for
the development of a new reliable model. Take the
following example:
Example 1. Consider a metric M which aims to
measure the security between the connections of the
MBAN buildings. Let A
t
be the set of buildings that
constitute the network. Consider two secure compo-
nents A
1
and A
2
of the metric such that: A
1
is a subset
of A
t
, where A
1
represents the number of buildings
that have firewall resources or another logical access
control and A
2
is a subset of A
t
, where A
2
represents
SECRYPT 2009 - International Conference on Security and Cryptography
382

the number of buildings that have ciphered connec-
tions.
Miani et al. states that the metrics formula, in this
case would be the arithmetic mean between the com-
ponents. However, we can consider the existence of
another subset A
3
with A
3
= A
1
∩ A
2
, in other words
A
3
is the set of buildings that have firewall resources
and encryption between connections. This new pa-
rameter must be part of the formula. For this consider
the number of security resources in a system, in gen-
eral, more quantity of security resources implies in
more security. In our case, the set A
3
has more secu-
rity resources then the sets A
1
and A
2
and hence, the
set A
3
will have a greater weight in relation to other
sets. Therefore, we can conclude that the intersection
quantity of a component must affect its weight.
This is the major motivation of this work, to de-
velop a standardized model capable of correcting the
inaccuracies of the model proposed by Miani et al.
and encourage its use in any kind of security metric.
4 MODEL DESCRIPTION
Take the set of the components a
1
, a
2
, a
3
, ..., a
n
. For
each a
i
, let a
t
be the maximum value that this mea-
sure assumes. Rewriting this sentence using the set
theory notation, we have one set for each compo-
nent a
1
, a
2
, a
3
, ..., a
n
. The correspondent a
t
will be
the set that contains the respective a
i
. Then, a
1
⊂ a
t1
,
a
2
⊂ a
t2
and so on.
The model objective is to increase the reliability
of the security index calculation. For this, the compo-
nents in the formula calculation will be balanced by
using different weights and another factor will be pre-
sented: the intersection component between the sets.
The first step to update the calculation of the for-
mula is to verify if the metric has a maximum compo-
nent or maximum value set, with two or more subsets.
Then, you should classify every metrics component.
The model proposed by Miani et al. states that,
given a metric M: i) M is composed only by secure
components, ii) M is composed only by insecure com-
ponents and iii) M is composed by insecure and se-
cure components
Let us first consider the case where the metric
is composed only by secure components. The other
cases will be deducted from this.
In cases where maximum value sets with two or
more related subsets do not exists, the formula cal-
culation is reduced to the mean between the compo-
nents. Here we only consider the existence of maxi-
mum value sets with at least two related subsets.
We begin the formula construction for the case
where the number of subsets of a maximum value set
is equal to 2, then the case where such number is 3
and at last the formula will be generalized. Consider
a metric M, consisting of a maximum value set T and
two sets A
1
and A
2
such that A
1
⊂ T and A
2
⊂ T. Let
I
1,2
be the set formed by the intersection between A
1
and A
2
. The cardinality, of these sets are: a
1
= #A
1
,
a
2
= #A
2
, i
1,2
= #I
1,2
and t = #T.
The formula for the case where the number of sub-
sets is 2, will be built using a weighted mean between
the subsets. The weights will be distributed as fol-
lows: 2 for the intersection component and 1 for the
other components. Note that the weight 2 represents
the number of subsets of T. Then the formula will be
written as:
F
2
=
(2)(
i
1,2
t
)+(1)(
a
1
t
)+(1)(
a
2
t
)
(2+1+1)
It is important to make an analysis of the maxi-
mum and minimum of the formula. A metric with
formula equal to 0 represents that no security require-
ments have been accomplished. Similarly, a metric
with formula equal to 1 represents that the security
requirements have been accomplished. However, for-
mula equal to 1, does not mean that security is fully
accomplished.
The maximum security is achieved when the num-
ber of elements of I
1,2
is equal to the number of ele-
ments of T, that is, i
1,2
= t. On the other side this
is only possible when A
1
= A
2
. If A
1
= A
2
then
I
1,2
= A
1
= A
2
and a
1
= a
2
= i
1,2
= t. Calculating
the formula, we obtain 1.
The minimum security is achieved if no security
requirements were met, that is, if A
1
= A
2
= I
1,2
= ∅.
Calculating the formula, we obtain 0.
In other words, the maximum and minimum anal-
ysis shows that the developed formula is consistent
with the defined requirements.
Consider a metric M, composed by a maximum
value set T and three sets A
1
, A
2
e A
3
such that A
1
⊂ T
, A
2
⊂ T and A
3
⊂ T and the intersection sets I
1,2
, I
1,3
,
I
2,3
and I
1,2,3
. The cardinality, of these sets are: a
1
, a
2
,
a
3
, i
1,2
, i
1,3
, i
2,3
, i
1,2,3
and t.
The weights will be distributed as follows: 3 for
the intersection set I
1,2,3
, 2 for the other intersection
sets, I
1,2
, I
1,3
and I
2,3
and at last 1 for the other sets.
Thus,
F
3
=
(3)(
i
1,2,3
t
)+(2)(
i
1,2
t
+
i
1,3
t
+
i
2,3
t
)+(
a
1
t
)+(
a
2
t
)+(
a
3
t
)
(3+2+2+2+1+1+1)
The same analysis of maximum and minimum
should be made here. Note that the results do not
change because the requirements for the maximum
security level is that I
1,2,3
= t that is, A
1
= A
2
= A
3
.
Now we can generalize the formula calculation for
the case where the number of subsets of T is n.
AN ALTERNATIVE APPROACH FOR FORMULA MODELLING IN SECURITY METRICS
383

Consider a metric M which is composed by one
maximum value set T with A
1
, A
2
, ..., A
n
subsets of
T. We denote the cardinality of this sets as follows:
a
j
= #A
j
.
The formula will be built using a general rule for
obtaining each of the terms. The term of weight n is
obtained by the ratio between the cardinality of the in-
tersection of the n subgroups and the cardinality of the
set T. The term of weight (n − 1) is obtained adding
all the ratios between the cardinality of the intersec-
tion of n− 1 sets and the cardinality of the set T. Con-
tinuing this process, all terms will be obtained. The
denominator is formed by the sum of the weights of
each of the terms. Each of the combinations C
n
k
rep-
resents the number of subsets in each of 1 to n terms.
A generalized version of the formula is:
F
n
=
n

i
1,...,n
t

+(n−1)

i
1,...,n−1
t
+...+
i
2,...,n
t

+...+
n(C
n
n
)+(n−1)
(
C
n
n−1
)
+...+(2)
(
C
n
2
)
+(1)
(
C
n
1
)
+
+
+...+2

i
1,2
t
+...+
i
n,n−1
t

+
(
a
1
t
+...+
a
n
t
)
n(C
n
n
)+(n−1)
(
C
n
n−1
)
+...+(2)
(
C
n
2
)
+(1)
(
C
n
1
)
However, we need to recall one last detail. The
formula is valid only for one maximum value set. For
m sets we should do the calculation for each one, and
then calculate the arithmetic mean between the re-
sults.
4.1 Differences between the Models
This section aims to show that the inclusion of
weights makes the model presented here more pre-
cise than the model proposed in (Miani et al., 2008).
In other words, the formula results presented in this
work are always smaller than the formula results pro-
posed by Miani et al. Consider the case where the
number of sets is equal to 2.
Let M be a metric composed by one maximum
value set T and two sets A
1
and A
2
such that A
1
⊂ T
and A
2
⊂ T. Let I
1,2
be the set composed by the inter-
section between the sets A
1
and A
2
.
Note that the following inequalities are valid:
i
1,2
≤ a
1
e i
1,2
≤ a
2
.
The formula presented by Miani et al. is given by
F
1
=
a
1
+a
2
2t
, and the formula proposed in this work is
given by F
2
=
2(i
1,2
)+a
1
+a
2
4t
.
Therefore, we would like to demonstrate that
a
1
+a
2
2t
≥
2t+a
1
+a
2
4t
. Using the proof by contradiction,
we obtain a
1
+ a
2
< 2i
1,2
This contradicts our assumption because, if we
sum the inequalities i
1,2
≤ a
1
and i
1,2
≤ a
2
we have
a
1
+ a
2
≥ 2i
1,2
. In this case, the formula proposed
in this work is always less or equal than the formula
proposed by Miani et al.
For the other cases the demonstration is analogue,
using the proof by contradiction in the obtained in-
equalities. The case that the number of sets is equal
to 3, for instance, the following inequality must be
proved:
a
1
+a
2
+a
3
3t
≥
3(i
1,2,3
)+2(i
1,2
)+2(i
1,3
)+2(i
2,3
)+a
1
+a
2
+a
3
12t
regarding the validity of the following inequali-
ties: i) i
1,2,3
≤ a
1
, i
1,2,3
≤ a
2
and i
1,2,3
≤ a
3
, ii)
i
1,2
≤ a
1
and i
1,2
≤ a
2
, iii) i
1,3
≤ a
1
and i
1,3
≤ a
3
and
iv) i
2,3
≤ a
2
and i
2,3
≤ a
3
.
5 RESULTS AND APPLICATION
EXAMPLE
In this section will be presented an application exam-
ple of the proposed model in security metrics found
in (ISO, 2005) and the case study, using the proposed
model in the Metropolitan Broadband Access Net-
work (MBAN) of Pedreira.
5.1 Application Example
Consider the metrics of the Communication and
Operations Management group, proposed in (ISO,
2005). Withinthis group we can identify three metrics
that can address the same security control: backup.
In our proposal, will be created a new group called “
Backup Policy” containing such metrics. The metrics
definition are,
1. Assets backed up: measures the percentage of
systems with critical information assets that have
been backed up in accordance with policy.
2. Assets backup validated: measures the percentage
of systems with critical information assets where
restoration from a stored backup has been suc-
cessfully demonstrated.
3. Assets backup offsite: measures the percentage of
backup media stored offsite in secure storage.
The metrics, separately, would be calculated as
follows. Consider a
t
= total number of assets, a
1
=
number of assets backed up, a
2
= number of assets
with backup procedures and validated a
3
= number of
assets whose backups are stored off-site. So, for the
first metric, we have
a
1
a
t
, for the second metric
a
2
a
t
and
finally for the third metric
a
3
a
t
. Note that the three com-
ponents, a
1
, a
2
and a
3
, have the same total value com-
ponent, number of assets, allowing that the proposed
SECRYPT 2009 - International Conference on Security and Cryptography
384

model may be applied here. Applying the model pre-
sented in this work, the new formula of the group “
Backup Policy” will be calculated like this:
F =
(3)(
i
1,2,3
t
)+(2)(
i
1,2
t
+
i
1,3
t
+
i
2,3
t
)+(
a
1
t
)+(
a
2
t
)+(
a
3
t
)
(12)
Thus, we have a security indicator for the whole
“Backup Policy” task. The model can be applied to
any set of metrics within requirements, easing the elu-
cidation of the results and producing an efficient and
balanced overview of a security question.
5.2 Metrics Application in the MBAN of
Pedreira
Metropolitan broadband access networks (MBAN)
can be defined as the convergence of services, appli-
cations and infrastructure to create a community com-
munications network of a city. This implements the
public information highway, characterized for high
bandwidth transmission capacity and data aggrega-
tion of several types (Mendes, 2006). Further infor-
mations about this kind of network can be found in
(Alexiou et al., 2006).
The MBAN of Pedreira is a project that has being
developed by the State University of Campinas (UNI-
CAMP) and by the governmentof the city of Pedreira.
The project started in 2005 and officially launched
in 2007. The detection of security vulnerabilities in
Pedreira’s network was the main motivation for the
development of particular metrics that could quantify
the high amount of data generated by technical reports
and management software. In next will be presented
the results of three security metrics applied in this pe-
riod. Also will be showed a comparison between the
two models discussed in this work. The metrics are:
i) Security between the MBAN buildings, ii) Security
requirements in the VoIP network and iii) Availability
and reliability in the MBAN servers.
Security between the MBAN Buildings
The aim here is to analyze and to increase security
level among the MBAN buildings. The formula com-
ponents are the following: a
t1
= total number of
buildings, a
1
= number of buildings that use fire-
wall resources or logical access control in their con-
nections, a
2
= number of buildings that use ciphered
resources in their connections and i
1,2
= number of
buildings that have both firewall resources and en-
crypted connections. The formula also have a factor
p that varies accordingly the size of the cryptographic
protocol used, attached to the a
2
component. The for-
mula is given by:
F
1
=
2
i
1,2
t
1
+
a
1
t
1
+p
a
2
t
1
4
Security Requirements in the VoIP Network
The objective here is to analyze the security require-
ments of the VoIP network in a MBAN. The formula
components are the following: a
t1
= total number of
VoIP branches, a
t2
= total number of VoIP calls in
a specific period, a
1
= number of VoIP branches ci-
phered, a
2
= number of VoIP branches which are in
separated networks from the data network, a
3
= num-
ber failed calls and i
1,2
= number of VoIP branches
both ciphered and in separated networks. The formula
is given by:
F
2
=
2

i
1,2
a
t1

+
(
a
1
a
t1
)
+
(
a
2
a
t1
)
(4)
+

1−

a
3
a
t2

2
Availability and Reliability in the MBAN Servers
The aim here is to evaluate the impact of the un-
planned downtime in the services deployed by the
MBAN servers. The formula components are the fol-
lowing: a
t1
= total number of servers, a
t2
= total
number of hours, a
1
= number of servers with re-
dundancy resources, a
2
= number of servers that are
in the backup program, a
3
= number of servers that
stores the backups in security offsite, a
4
= uptime
mean of servers and i
1,2
= number of servers with
both redundancy and in the backup program. The for-
mula is given by:
F
3
=
2

i
1,2
a
t
1

+
(
a
1
a
t1
)
+
(
a
2
a
t1
)
(4)
+

a
3
a
2

+

a
4
a
t2

3
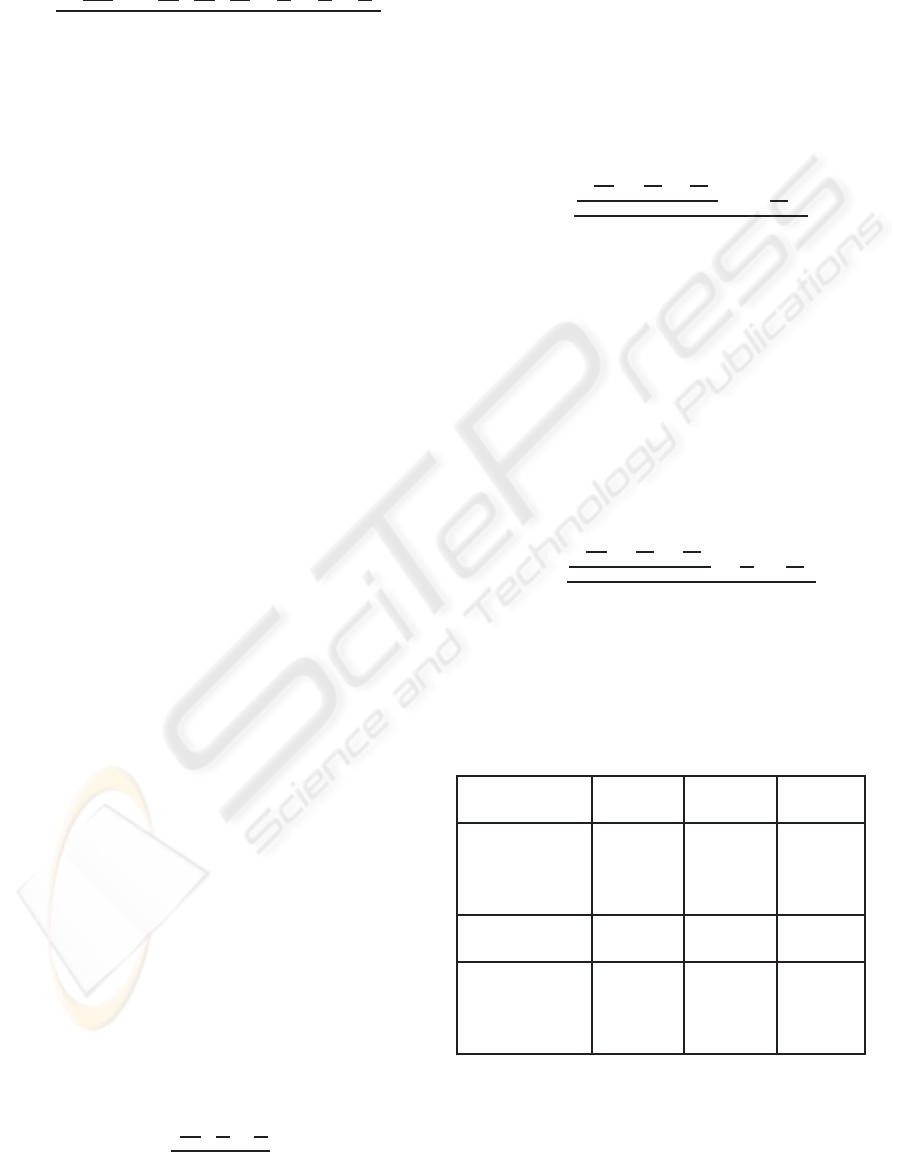
Table 1 shows the result of each one of the metrics
and also compares with the model proposed by Miani
et al. We denote Model 1 for the model proposed by
Miani et al. and Model 2 for the model proposed in
this work.
Table 1: Metrics results and comparison.
Metric
Formula
Model 1
Formula
Model 2
Decrease
Security
between the
MBAN
buildings
0.5411 0.3117 42.39%
VoIP security
requirements
0.7296 0.6046 17.13%
Server’s
availability
and
reliability
0.7496 0.7217 3.72%
According to what was showed in section 4.1, the
model proposed here achieved lower results. The col-
umn “Decrease” illustrates the difference between the
results of the two models. This difference is obtained
AN ALTERNATIVE APPROACH FOR FORMULA MODELLING IN SECURITY METRICS
385

from the values of the component intersection. Higher
values imply in the decrease of distance between the
formulas. Similarly, lower values imply in the in-
crease of distance between the formulas.
Besides the intersection component, the way that
the metrics formula is obtained can also influence on
the difference between the models. If the formula has
components that require in its composition the inser-
tion of additional arithmetic mean, such as have si-
multaneously secure and insecure components (met-
ric 2) or have components outside the intersection
(metric 3), these components will act as follows: val-
ues near to 1 decrease the difference and values near
to 0 increase the difference.
6 CONCLUSIONS
Security metrics are modern tools and with high re-
search potential. They are extremely important for the
security level understanding of the organization when
properly developed and applied.
A classic security metric has several components,
including: objective, data source, frequency, classifi-
cation and formula. The purpose of the formula, in
particular, is to describe the calculations to be per-
formed for quantify the metrics in a numerical expres-
sion. That is, the metrics results are investigated from
the formula. It is important that this task be accom-
plished in a clear, robust and generic way.
The model proposed in this work sought to cor-
rect the inaccuracies of the model proposed by Miani
et al. developing a new component, which deals with
sets intersections of security measures. This compo-
nent plays an important role in the model, distribut-
ing the weights in the proposed formula. Besides the
formula, the whole nomenclature and the logic con-
struction developedin this work can be reused to build
other models in this area.
The model validation it was obtained in two ways:
from the metrics application found in literature and
with a case study. Classic security metrics as found
in (Jaquith, 2007), (Swanson et al., 2003) and (ISO,
2005) are easily migrated to our model. One of the
benefits is the aggregation of various measures in only
one, easing the overview and the results interpretation
of the non-technical organization staff. Besides that,
the proposed model was used in three security metrics
that were implemented in the MBAN of Pedreira. The
results showed that the model proposed here achieved
lower results when compared to Miani et al. model
and could also explain how the numerical differences
between the models are established.
Future works includes the model utilization in
other security metrics, aiming to create its own cata-
log, suchlike what is developed in the Metrics Catalog
Project (MetricsCenter, 2008) and the application of
new case studies to refine the proposed model in pri-
vate institutions, government and other MBANs en-
abling the development of a security metrics database.
REFERENCES
Alexiou, A., Bouras, C., and Primpas, D. (2006). Design
aspects of open municipal broadband networks. In
AcessNets ’06: Proceedings of the 1st international
conference on Access networks, page 20, New York,
NY, USA. ACM Press.
Herrera, S. (2005). Information security management met-
rics development. In Security Technology, 2005.
CCST ’05. 39th Annual 2005 International Carnahan
Conference on, pages 51–56.
ISO (2005). Code of practice for information security man-
agement - iso/iec 27002.
Jaquith, A. (2007). Security Metrics - Replacing Fear, Un-
certainty and Doubt. Addison-Wesley.
Jelen, G. and Williams, J. (1998). A practical approach to
measuring assurance. In Computer Security Applica-
tions Conference, 1998, Proceedings., 14th Annual,
pages 333–343.
Lowans, P. W. (2002). Implementing a network security
metrics program. Technical report, SANS.
Mell, P., Scarfone, K., and Romanosky, S. (2007). A com-
plete guide to the common vulnerability scoring sys-
tem version 2.0. http://www.first.org/cvss/.
Mendes, L. S. (2006). Infovia Municipal - Um novo
Paradigma em Comunicaes. Universidade Estadual
de Campinas.
MetricsCenter (2008). http://www.metricscenter.org/
index.php/plexlogicmetricviewer. Accessed in
24/02/2009.
Miani, R. S., Zarpelo, B. B., de Souza Mendes, L., and Jr.,
M. L. P. (2008). Metrics application in metropolitan
broadband access network security analysis. In SE-
CRYPT 2008 - International Conference on Security
and Cryptography, pages 473–476.
Payne, S. C. (2006). A guide to security metrics. SANS Se-
curity Essentials GSEC Practical Assignment Version
1.2e.
Rosenblatt, J. (2008). Security metrics: A solution in search
of a problem. EDUCAUSE Quarterly, 3:8–11.
Swanson, M., Bartol, N., Sabato, J., Hash, J., and Graffo, L.
(2003). Security metrics guide for information tech-
nology systems. Technical report, NIST Special Pub-
lication 800-55.
Weiss, S., Weissmann, O., and Dressler, F. (2005). A com-
prehensive and comparative metric for information se-
curity. In Proceedings of IFIP International Confer-
ence on Telecommunication Systems, Modeling and
Analysis (ICTSM2005), pages 1–10.
SECRYPT 2009 - International Conference on Security and Cryptography
386