EFFICIENT ALGORITHMS AND ABSTRACT DATA TYPES FOR

LOCAL INCONSISTENCY ISOLATION IN FIREWALL ACLS

S. Pozo, A. J. Varela-Vaca, R. M. Gasca and R. Ceballos

Department of Computer Languages and Systems. Computer Engineering College

University of Seville. Avda. Reina Mercedes S/N, 41012 Seville, Spain

Keywords: Isolation, Inconsistency, Conflict, Anomaly, Firewall, ACL, Ruleset.

Abstract: Writing and managing firewall ACLs are hard, tedious, time-consuming and error-prone tasks for a wide

range of reasons. During these tasks, inconsistent rules can be introduced. An inconsistent firewall ACL

implies in general a design fault, and indicates that the firewall is accepting traffic that should be denied or

vice versa. This can result in severe problems such as unwanted accesses to services, denial of service,

overflows, etc. However, the administrator is who ultimately decides if an inconsistent rule is a fault or not.

Although many algorithms to detect and manage inconsistencies in firewall ACLs have been proposed, they

have different drawbacks regarding different aspects of the consistency diagnosis problem, which can

prevent their use in a wide range of real-life situations. In this paper, we review these algorithms along with

their drawbacks, and propose a new divide and conquer based algorithm, which uses specialized abstract

data types. The proposed algorithm returns consistency results over the original ACL. Its computational

complexity is better than the current best algorithm for inconsistency isolation, as experimental results will

also show.

1 INTRODUCTION

A firewall is a network element that controls the

traversal of packets across different network

segments. It is a mechanism to enforce an Access

Control Policy, represented as an Access Control

List (ACL).

One of the most important and frequent faults

during firewall ACL design and management are

inconsistencies (Wool, 2004) (Pozo2, 2008). A

firewall ACL with inconsistent rules implies in

general design faults, and indicates that the firewall

is accepting traffic that should be denied or vice

versa. This can result in severe problems such as

unwanted accesses to services, denial of service,

overflows, etc. ACL consistency is of extreme

importance in several contexts, such as highly

sensitive applications (e.g. health care). Thus,

algorithms and tools to automatically isolate and

characterize inconsistencies must be provided in

order to give firewall administrator enough

information to correct them and reduce the number

of faults in firewall ACLs. In this paper we are only

interested in layer 3 firewall ACLs, and thus in the

five typical selectors (Taylor, 2005): protocol,

source and destination IPs, and source and

destination ports.

Many algorithms to isolate and characterize

inconsistencies in firewall ACLs have been

proposed, but it is the firewall administrator who

ultimately decides which rules have to be corrected.

However, these algorithms have many drawbacks

regarding different aspects of the consistency

diagnosis problem. One of the most important ones

is that they pre-process the firewall ACL using

different types of non-trivial decompositions in

order to use more efficient abstract data types and

techniques. However, these decomposition

techniques increase the number of rules in the ACL

and have worst-case exponential time and space

complexity. As a consequence, results of these

consistency management algorithms are given over

the modified ACL. Time and space complexity of

inconsistency isolation algorithms is very important,

since these algorithms are being used in a new range

of applications in resource-constrained devices in

ubiquitous networks, such as ad-hoc network node

real-time ACL updates, real-time IDS or IPS rule

updates, etc.

Pozo S., J. Varela-Vaca A., M. Gasca R. and Ceballos R. (2009).

EFFICIENT ALGORITHMS AND ABSTRACT DATA TYPES FOR LOCAL INCONSISTENCY ISOLATION IN FIREWALL ACLS.

In Proceedings of the International Conference on Security and Cryptography, pages 42-53

DOI: 10.5220/0002233100420053

 SciTePress

To the best of our knowledge, there are only two

algorithms that do not decompose the ACL: the

trivial one (which is worst case O(f

) time

complexity with the number of rules in the ACL, f);

an optimization over the trivial one (Pozo2, 2008),

which only improves the average and best cases by

an order of magnitude in best and average cases.

However, the best algorithm to date (which

decompose the ACL) represents an improvement

over 30 times (on average) over the trivial one

(Baboescu, 2003).

In this paper we propose a rule-order

independent inconsistency isolation algorithm. Our

approach is based on an analysis of which data type

each rule selector can store, on the design of

specialized abstract data types for each one, and on

divide and conquer algorithm. Worst-case

computational complexity of the algorithm proposed

in this paper is better in all cases than Baboescu one,

as is going to be shown in both theoretical

complexity analysis and experimental results with

real ACLs. Furthermore, ACL pre-process is not

needed by our algorithm and thus results are

returned over the original, unmodified ACL.

This paper is structured as follows. In section 2,

we review related works comparing them to our

proposal. In section 3 we briefly analyze the

internals of the consistency diagnosis problem in

firewall ACLs. In section 4 we explain the

methodology followed to solve the problem, and

propose abstract data types (ADTs) and algorithms,

with their theoretical complexity analysis. In section

5, we give experimental results with real ACLs,

comparing these results with other proposals. In

section 6 we give some concluding remarks.

2 RELATED WORKS

The closest works to ours are related with

consistency isolation in general network filters. In

the most recent work, (Baboescu, 2003) provides

algorithms to detect inconsistencies in router filters

that are worst-case 30 times (an order of magnitude)

faster than O(f

) ones for the general case of any

number of selectors per rule, where f is the number

of rules in the ACL. Although a theoretical

complexity analysis is not provided, it improves

other previous isolation algorithms for k filters

(Eppstein, 2001) (Hari, 2000). Baboescu proposal

implies ACL decomposition as a pre-process,

converting selector ranges to prefixes (Srinivasan,

1998). Nevertheless, the range to prefix conversion

technique could need to split a range in several

prefixes and thus the final number of rules could

increase over the original ACL. In (Gupta, 1999)

(Taylor, 2005), Taylor and Gupta outlined that this

kind of conversion could be inefficient, because

transport layer specifications vary widely (for

example it possible to specify open port ranges, such

as “all ports greater than 1023”). Taylor also

calculated that, in the worst case, a range covering

w-bit port numbers may require 2(w-1) prefixes, and

that a single ACL including only two port ranges

could require 2(w-1)

entries (900 entries for 16-bit

port numbers, increasing the number of rules in the

ACL. Thus, inconsistency isolation results are given

over the modified ACL, which is bigger and

different that the original one. Baboescu also

calculated ACL size increase for its data set in his

paper.

Other researchers have analyzed the minimal

inconsistency diagnosis problem. This problem is

different to the inconsistency isolation one, since

isolation is the action of finding the rules that are

inconsistent with other ones, and is a polynomial

problem. However, inconsistency diagnosis also

implies the identification of the minimal number of

rules which are the cause of the isolated

inconsistencies (Pozo2, 2008), and the minimal

characterization of the diagnoses among an

established taxonomy (Hamed, 2006). The

consistency diagnosis problem consists in the

resolution of these three problems (isolation,

identification, characterization) plus a correction

stage (if necessary).

These researchers apply ACL decompositions in

some cases, and combinatorial algorithms in others,

in order to optimally solve the three problems at a

time. Decompositions are used in (Al-Shaer, 2004)

and in (García-Alfaro, 2008), which use ACL

decorrelation (Luis, 2002). As with range to prefix

conversion, ACL decorrelation increase the number

of rules in the ACL and have worst-case exponential

time and space complexity. As a consequence,

results of the consistency management algorithms

are given over the modified ACL.

Ordered Binary Decision Diagrams (OBDDs)

have been used in Fireman (Yuan, 2006). Fireman

authors’ do not decorrelate the ACL, and thus,

results are given over the original one. Note that the

complexity of OBDD algorithms depends on the

optimal ordering of its nodes, which is a NP-

Complete problem (Bollig, 1996). This results in

worst case exponential complexity, as with other

proposals for the consistency diagnosis problem.

EFFICIENT ALGORITHMS AND ABSTRACT DATA TYPES FOR LOCAL INCONSISTENCY ISOLATION IN

FIREWALL ACLS

3 CONSISTENCY IN FIREWALL

ACLS

Firewall rule-matching engines match packets in a

linear way, checking rules from the first one to the

last. The matching process stops once a rule has

been matched, or once there are no more rules in the

ACL (in this case, the firewall platform executes a

predefined default action). The values of selectors

(or filtering fields) between different rules can

overlap, and can even be rules that are completely

equal to others. An example of an ACL is presented

in Fig. 2. In this example,

43RR⊂ , because all

selectors of R4 are at least subsets of the same

selectors of R3. However, their actions are the

opposite. In this case R4 is never going to be

matched in this ACL, because all packets that R4

could match are also matched by a rule with higher

priority, R3. In this case, the firewall administrator

must be notified, since R3 may be a faulty rule (the

consequence, or the error, is that there is traffic that

is denied by R3 and it may be accepted). As another

example take rules R1 and R2,

12RR⊂ . In this

case traffic that is denied by R1 is also accepted by

R2. This kind of relation is used by administrators to

express exceptions (the most specific rule, R1) to a

general rule (R2), and is not usually considered to be

a fault, because there is no error in the ACL

execution.

Note that in these two examples, actions are

always different (in firewalls there only two possible

actions: to allow or to deny a packet). If actions were

equal, there is no potential erroneous behaviour in

the executed ACL, and thus there is no

inconsistency. However, in this case, the relation

between the rules is a redundancy, which is another

kind of problem that can reduce the performance and

increase the memory consumption of the rule-

matching engine. In this paper, we are only

interested in rules that be potential faults, or

inconsistent rules [4] (there could be cases where a

rule is inconsistent with many others). It must be

clarified that inconsistencies are order-independent

and mutual. We assume that ACL

do not have

redundancies (redundancies can be efficiently

detected and removed (Liu, 2008))

3.1 Problem Formalization

A layer 3 Firewall ACL is in general a list of linearly

ordered (total order) condition/action rules. Each

rule firewall rule is formed by an antecedent and a

(binary) consequent representing the action that

must be taken once a packet matches the rule.

Let PORTSRC and PORTDST be sets of natural

numbers and intervals of naturals between

[0..65535] representing a port number. Le IPSRC

and IPDST be two sets of valid IPv4 addresses in the

octet and CIDR format (o1.o2.o3.o4/CIDR). Let

PROTOCOL be a set of natural numbers in [0..255]

representing a protocol number. Let ID≥1 be a

natural number representing the rule priority in the

ACL (1 is the rule with more priority). These five

sets plus the ID represent the typical selectors of a

firewall rule [3]. Let ACTION={Allow, Deny} be the

binary set of possible actions for a rule consequent.

Let W=PROTOCOL×IPSRC×IPDST×PORTSRC×

PORTDST be the cartesian product of the five

previous sets or selectors, which represents a 5-

dimensional hypercube. W is the space where an

antecedent of a firewall rule can be defined. Layer 7

firewalls use different selectors (e.g. a selector to

express the content of a packet) and thus needs a

different problem analysis.

Definition 3.1. A layer 3 firewall ACL or rule set, is

defined as the cartesian product ACL

=W×ACTION,

where |ACL

|=f. A rule in ACL

is defined as

RACL kf

∈

≤≤ , kID∈ where

[PROTOCOL], R

[IPSRC], R

[IPDST],

[PORTSRC], R

[PORTDST] represent the

corresponding selectors of the rule.

Definition 3.2. ACL

can be trivially divided in two

disjoint sets, one composed of rules with Allow

action (ACL

allow

, where |ACL

allow

|=m), and the other

composed of rules with Deny action (ACL

deny

, where

|ACL

deny

|=n). Thus

allow deny f

CL ACL ACL=∪ and

allow deny

ACL ACL

∅

∩

Definition 3.3. Let the antecedent of a rule of

RACL

∈

defined as an element or subset of W,

()

aR W⊆ . Let the consequent of a rule

RACL

∈

be defined as ()

c R Allow Deny=∨.

The union of the antecedents of all rules in

ACL

allow

is the set

()

i allow

AaRACL=∈

∪

. The union of

the antecedents of all rules in

ACL

deny

is the set D,

()

deny

DaRACL=∈

∪

Definition 3.4. Inconsistency Detection.

()()

iallowjdeny

aR ACL aR ACL

∈

∈≠∅∩ iff R

and R

are mutually inconsistent, I(R

, R

) |− ⊥. Since two

elements in ACL

representing an action and the

contrary over a subset of W are logically

inconsistent. In the same way ACL

is inconsistent

SECRYPT 2009 - International Conference on Security and Cryptography

Priority/ID Protocol Source IP Src Port Destination IP Dst Port Action

R1 tcp 192.168.1.5/32 any *.*.*.*/0 80 deny

R2 tcp 192.168.1.*/24 any *.*.*.*/0 80 allow

R3 tcp *.*.*.*/0 any 172.0.1.10/32 80 allow

R4 tcp 192.168.1.*/24 any 172.0.1.10/32 80 deny

R5 tcp 192.168.1.60/32 any *.*.*.*/0 21 deny

R6 tcp 192.168.1.*/24 any *.*.*.*/0 21 allow

R7 tcp 192.168.1.*/24 any 172.0.1.10/32 21 allow

R8 tcp *.*.*.*/0 any *.*.*.*/0 any deny

R9 udp 192.168.1.*/24 any 172.0.1.10/32 53 allow

R10 udp *.*.*.*/0 any 172.0.1.10/32 53 allow

R11 udp 192.168.2.*/24 any 172.0.2.*/24 any allow

R12 udp *.*.*.*/0 any *.*.*.*/0 any deny

Figure 1: Example of a Firewall ACL.

iff AD≠∅∩ . Consistency is not affected by the

relative priority between rules. An inconsistency is

considered to be a fault if an administrator identifies

the behaviour of the executed ACL as being causing

undesirable effects (or having errors).

Definition 3.5. Inconsistency Isolation. It is to find

out all

i allow

RACL∈ ,

jdeny

RACL

∈

such that I(R

) |− ⊥.

The objective of the algorithm proposed in this

paper is to isolate (Definition 3.4) the elements in

ACL

allow

and ACL

deny

which are mutually

inconsistent (Definition 3.5). The trivial algorithm

consist in checking all pairs of rules in ACL

that are

consistent with Definition 3.4, which is in O(f

), or

to check rules in the set A with rules in the set D

with (again with Definition 3.5), which is in O(n·m).

Our algorithm depart from ACL

allow

and ACL

deny

with

|| | |

deny allow

ACL ACL< (and thus n<m) (if

|| | |

deny allow

ACL ACL< , results and explanations

are analogous), and is based on divide and conquer

algorithm:

Each set M

contains the ID selector of rules in

ACL

allow

that intersect with a given rule

ideny

RACL∈

Thus, the result of the isolation process consists

of several M

sets, where each one contains the IDs

of the inconsistent rules in ACL

deny

for a given rule

of ACL

allow

. A set M

is empty iff R

is consistent.

This result can be trivially decomposed to obtain all

pairs of inconsistent rules in ACL

Figure 2: Result of the inconsistency isolation process.

This result can be used directly by the firewall

administrator, or as input to an inconsistency

identification process (Pozo2, 2008), resulting in a

diagnosis that can be characterized. There is a

complete taxonomy for firewall ACL inconsistencies

available in (Hamed, 2006). We are interested in all

kinds of inconsistencies, independently of their

characterization, since all of them are equally

important for the firewall administrator (who is the

responsible of deciding if they are considered faults

or not).

4 INCONSISTENCY ISOLATION

PROCESS

An extensive analysis of the market-leader firewall

languages was presented in (Pozo1, 2009). In the

analysis it was shown that IP addresses can be

expressed by all of them in octets with a CIDR value

(IP blocks), port numbers as naturals or intervals of

naturals, and protocols as a natural number. Thus,

each selector although being different by nature, can

,,,

([])

deny

id i i

ACL

ROTOCOL IPSRC IPDST

PORTSRC PORTDST

ARj M

≤≤

∀∈

⎧⎫

∀∈

⎨⎬

⎩⎭

∩≠∅=

∏

PROTOCOL IPSRC

IPDST PORTSRC PORTDST

MMj

⎧⎫

=∈

⎨⎬

⎩⎭

∩

EFFICIENT ALGORITHMS AND ABSTRACT DATA TYPES FOR LOCAL INCONSISTENCY ISOLATION IN

FIREWALL ACLS

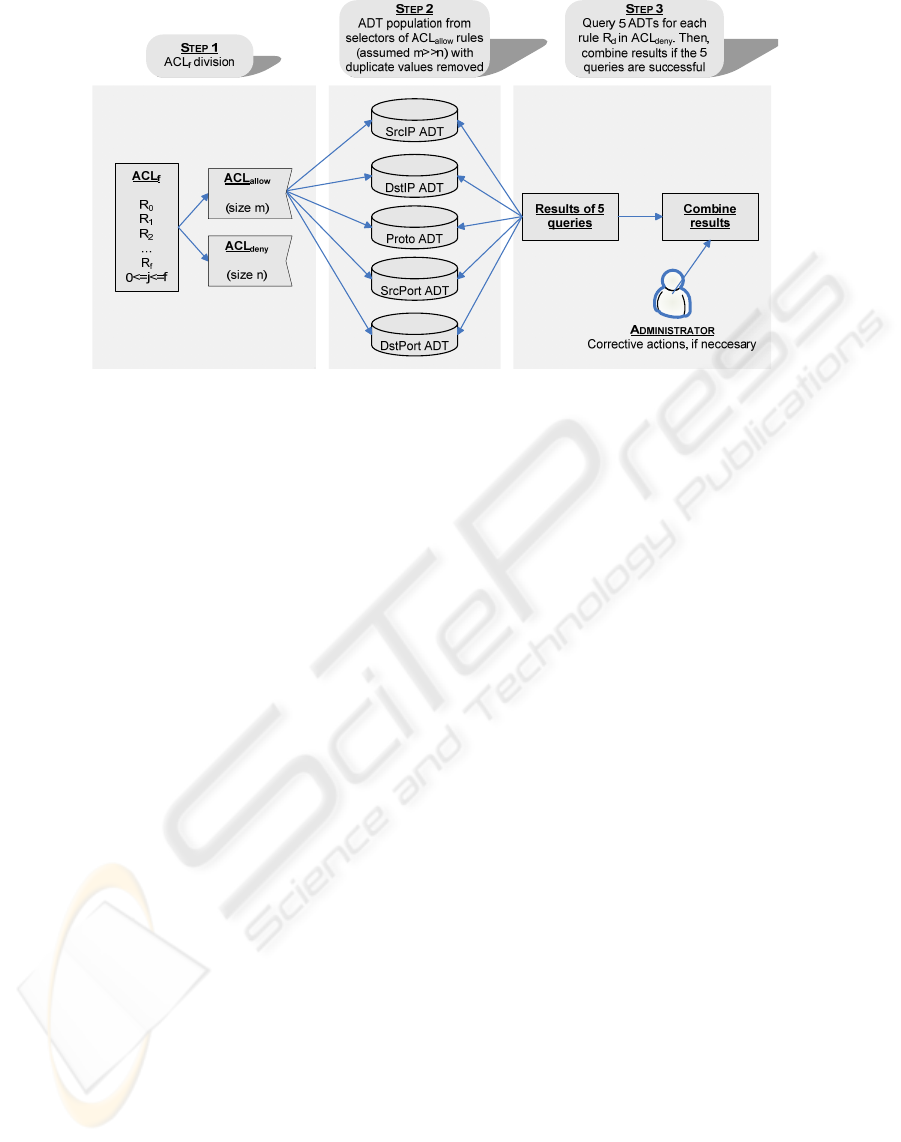
Figure 3: Proposed inconsistency isolation process.

be expressed as natural numbers and, in some cases,

as intervals of naturals.

One of the main ideas of our approach is to use a

specialized abstract data type (ADT) to store the set

of all selectors of the same type of the m rules in

ACL

allow

(i.e. one ADT to store protocols used in all

rules, two ADTs to store the source and destination

IPs used in all rules, and another two ADTs to store

source and destination ports). With this division and

using divide and conquer, in order to know with

which rules in ACL

allow

the rule

ddeny

RACL∈ is

inconsistent with, it is needed a search in each ADT

for each selector in R

. Each of these five searches

returns all rules which have an intersecting selector.

However, not all of these rules are inconsistent with

, a final combination step is needed. Attending to

the presented inconsistency definitions, R

inconsistent with one or more rules in ACL

allow

only

if all of its selectors intersect with all the selectors of

one or more rules in ACL

allow

. Thus, the results of

the five searches must be intersected in order to get

this information. Since the process must be repeated

for the n rules in ACL

deny

, this complexity must be

multiplied by n. The whole process is graphically

represented in Fig. 3.

In the following sections, a different data

structure is going to be proposed for each selector,

based on the analysis of the particular data set that

each one can store (Pozo1, 2009). The objective is to

find or design ADTs capable of doing searches in

worst case time complexity better or equal than

O(logm). Finally, a combination step for these

search results in worst case time complexity in O(r)

is also going to be proposed, where r=m/k, and

where k a very big constant (k≥128) which is going

to be theoretically calculated. So, the final time

complexity of the algorithm is in worst case

O(f

/4k). Note that in the worst case, n=m=f/2 (i.e.

ACL

has half rules with allow action, and the other

half with deny). As we have said at the beginning of

the section, we have assumed that m>n. However, if

n>m, the algorithm can adapt itself and use ACL

deny

rules (instead of ACL

allow

ones) to instantiate ADTs.

That is, the algorithm always dynamically takes the

bigger of the two ACLs for ADT instantiation.

Since the ADTs are only populated once,

insertion time for each ADT is amortized during

search operations. Also take into account that if the

ACL is going to be updated (new rules are inserted,

modified, or removed), ADT operations for updates

are necessary. However update operations have not

been considered, since updates are not the focus of

this paper, but a topic for future research. The

presented isolation process is thus considered static.

4.1 ADT for Protocol Number Selector

Attending to the exhaustive analysis of real firewall

languages presented in an earlier work (Pozo1,

2009) the protocol selector only admits 8-bit natural

numbers and the wildcard, ‘*’. Although symbolic

names are also possible, they can be converted to

naturals using IANA protocol number list

(RFC5237). An important fact is that no ranges are

allowed in the syntax of the selector, and thus search

is a trivial operation, since in order to find a non-

empty intersection with a protocol number (the one

of rule

ddeny

RACL∈ ) there are only two possible

coincidences in the ADT: ‘*’; or exactly the same

value. In the case that Rd protocol number is ‘*’,

SECRYPT 2009 - International Conference on Security and Cryptography

then R

intersects with all rules of the ADT, that is

all rules in ACL

allow

, and no search is necessary.

To store the association <Protocol number, Rule

ID> we propose to use a hash table with protocol as

the key, and the rule IDs as value. Hash tables

(Cormen, 2001) have O(1) (constant) time

complexity for insertions, removals, updates, and

search operations if a perfect hash function is used.

A perfect and minimal hash function is possible,

since the key space is limited and known in advance

(from 0 to 65535, plus the ‘*’). Hash table

instantiation is thus worst case O(n) (the number of

rules in ACL

allow

However, hash tables cannot store duplicate

keys. This is an important problem, since in most

real-life firewall ACLs only a few protocol numbers

are used, although they could be thousand of rules in

the ACL. This issue can be solved grouping all

protocol selectors of the rules that share the same

value (the same key). In this case, the associated

value to the key is a set containing the rule IDs of all

rules that have the key value as the value of their

protocol selector. However, as removal of values

could be inefficient in this way (a hash lookup plus a

search in the list of rule IDs), instead of a list, it is

used a fixed-size bit set of size m (the size of

ACL

allow

). Each position of the bit set represents one

of the m rules in ACL

allow

. Positions are set to ‘1’ for

the rules in the hash table that share the same

protocol number. As a side effect, with only one

lookup operation in the hash table, all rule IDs that

share the same protocol number are returned, as the

bit set is the return result of search operations.

Fig. 4 presents the hash table associated to Fig. 1

example, and the result of all the possible search

operations using the same protocol selector values of

ACL

deny

rules. In order to simplify the figure, only

the set positions of bit sets are represented (rule IDs

of the assigned rules have been directly used).

Furthermore, protocol names have been transformed

to IANA protocol numbers in the rightmost part of

the figure.

4.2 ADT for Port Number Selectors

Again, attending to the syntax analysis of market-

leader firewall languages (Pozo1, 2009), the port

selectors admit 16-bit natural numbers, double-

ended closed natural intervals, and ‘*’. Symbolic

names are converted to naturals or intervals. Source

and destination port selectors are treated the same

way from ADT and complexity viewpoint, and thus

the discussion is applicable for both.

As with the protocol selector, the result of the

search operation for port numbers is all rule IDs of

ACL

allow

which have an intersecting port number

with

ddeny

RACL∈ . In this case, a hash table is

useless, since searching a port or an interval in it will

only return equality result, but not intersections with

port intervals. For example, in a hash table with keys

{80, 79-81} and the port of R

is 80, the search

operation would return only the rule IDs associated

to port 80 key, but note that port 80 also intersects

with the interval 79-81. In the same way, if the port

of R

is the interval [81-82], then no value will be

returned, since the interval [81-82] is not stored in

the hash table. Searching the entire hash table would

return the needed result, but this operation has a

linear time complexity with the number of different

keys in the hash table.

ACL

allow

(proto=tcp)

(proto=udp)

, V

> = <6, {R

, R

, V

> = <17, {R

, R

ASH TABLE

ACL

deny

(proto=tcp)

(proto=udp)

RESULTS

Search(R

)={R

, R

}

Search(R

)={R

, R

}

Search(R

)={R

, R

}

Search(R

)={R

, R

}

Search(R

)={R

, R

}

Figure 4: Hash table (perfect and minimal hash function)

of protocol selector of Figure 1 example (ACL

allow rules)

and search results for ACL

deny rules.

There are two well-known 2D problems in

computational geometry that solve similar searches

(Chiang, 1991): first, given a set of data points (port

numbers) and a query rectangle (port interval), give

all the points that are inside the rectangle (this is the

orthogonal range search problem); second, given a

set of (possibly intersecting) data rectangles (port

intervals) and a query point (port number), give all

rectangles that intersect the query point (this is the

stabbing problem).

These two 2D problems can be reformulated into

1D space, where rectangles are intervals and points

are only represented by one coordinate. In 1D, these

problems are called 1D range search problem (de

Berg, 1997) and overlapping interval search

problem (Edelsbrunner, 1983) (EdelsBrunner2,

1983) respectively. Fortunately, specialized data

structures for 1D and 2D problems that give optimal

EFFICIENT ALGORITHMS AND ABSTRACT DATA TYPES FOR LOCAL INCONSISTENCY ISOLATION IN

FIREWALL ACLS

bounds (in time and space) solutions to these two

problems exist (Chiang, 1991). In the particular case

of 1D, the Interval Tree (Cormen, 2001)

(Edelsbrunner, 1983) (EdelsBrunner2, 1983), or

ITree, is the selected ADT because it has optimal

bound for the 1D problem (in time and space).

Fortunately, our port number or port interval

search problems can trivially be reformulated to

range search and overlapping interval search

problems respectively, as port numbers can be

represented as points in a 1D plane, and port

intervals can be presented as lines in the same 1D

plane.

Let X be a set of M points in a line, and S a set of

m segments with endpoints in X. The primary

structure for the ITree, T, can be a balanced binary

search tree (Chiang, 1991) or a red-black tree

(Cormen, 2001), whose internal nodes store the

points of X, sorted from left to right, and whose

leaves represent intervals between consecutive

points of X. Each segment s of S is allocated at the

least common ancestor of the nodes associated with

the endpoints of s. The set of segments allocated at a

node b, denoted by S(b), is represented by two lists

that store the left endpoints sorted from left to right,

and the right endpoints sorted from right to left.

Hence, the space complexity is in O(m+M). In our

problem, this is linear with the number of rules in

ACL

allow

. Furthermore, in our implementation

duplicate intervals or points are not allowed (as with

duplicate protocols), and are only stored once (again,

using a bits set for rule IDs). Thus, the space

complexity is reduced in a constant factor.

ITrees are static ADTs, where only a fixed set of

segments and points, known in advance, can be

stored. However, in order to support insertions and

deletions of segments and points, the endpoint lists

can be replaced with inorder-threaded balanced

search trees. Hence, the update time is in amortized

O(logm). Query time is in O(logm + L), where L is

the number of returned results (a constant factor).

Thus, instantiation is in worst case amortized

O(m*logm), one insertion for each rule in ACL

allow

Best case time complexity could be very small when

the number of port repetitions between different

rules is very high, since the resulting ITree would be

very small. ITrees is a well-know ADT, which has

been widely used in database searches. Due to space

constraints, no more information will be presented

here, but it is available in the given references,

including a time and space complexity analysis.

The result of the search operation over the ITree

with a port number or interval of the rule

ddeny

RACL∈ , is the union of all bit sets associated

to port values in the ITree which intersect the given

port of R

, or a bit set with all bits set to ‘1’ if the

given port of R

is ‘*’. Fig. 5 presents the ITree

associated to Fig. 1 example (destination port

selector of ACL

allow

only), and the result of all the

possible search operations using destination port

selector of Fig. 1 ACL

deny

rules.

ACL

allow

(dport=80)

(dport=21)

(dport=53)

(dport=*)

ACL

deny

(dport=80)

(dport=21)

(dport*)

(dport=*)

RESULTS

Search(R

)={R

, R

}

Search(R

)={R

, R

}

Search(R

)={R

, R

}

Search(R

)={R

, R

}

Search(R

)={R

, R

}

[0-65535]

}

[21,21]

, R

}

[80,80]

, R

}

[53,53]

, R

}

INTERVAL TREE

Figure 5: Interval tree of destination port selector of

Figure 1 example (ACL

allow rules) and search results for

ACL

deny rules.

4.3 ADT for IP Address Selectors

Attending to the syntax analysis of firewall

languages (Pozo1, 2009), both IP address selectors

admit 32-bit host IP addresses in CIDR format, and

‘*’. Symbolic names are converted to octets. Source

and destination IP selectors are treated the same way

from ADT and complexity viewpoint, and thus the

discussion is applicable for both.

As with previous cases duplicates are not

allowed (bit sets are used again). Thus, the result of

the search operation must be a bit set with positions

set to ‘1’ for all rule IDs of ACL

allow

which have an

intersecting IP with the given in the rule

ddeny

RACL∈ . As an IP block is a compact way of

expressing IP address intervals, a hash table is again

useless for IPs. An IP address is composed by four

octets, each one being an 8-bit natural. A search

operation over an ADT must use the CIDR of the

IPs stored in it: Let IP

/CIDR

and IP

/CIDR

be two

IP addresses, if CIDR

is the shortest of the two

SECRYPT 2009 - International Conference on Security and Cryptography

netmasks, then the intersection of IP

and IP

is not

empty if IP

&CIDR

=IP

&CIDR

Note that valid network IP addresses have CIDR

values between 1 and 30. Value 31 is useless, since

it only permits two hosts (.0 and .255, which are not

valid host IP addresses); CIDR 32 is reserved for

host IPs; and CIDR 0 is only used for the wildcard

IP (0.0.0.0/0).

We propose the design of a completely new and

specialized ADT to store IP addresses, capable of

doing searches that return multiple intersections (as

with previous selectors) in time better than O(m)

(where m is the size of ACL

allow

). As we are going to

show, space complexity of this ADT is better than

O(m). This new ADT is called IP Tree. The general

structure of an IP Tree as well as several example

IPs and its corresponding IP Tree are presented in

Figures 6 and 7 respectively.

The IP Tree is formed by four levels (root is not

considered to be a valid level). For each node, 255

children are possible at most (0-254). These children

values of each node (octets) are recursively stored in

a hash table (with a perfect and minimal hash

function). The association <Node octet, Children

nodes> is called an IP Tree node, where children

octets is another hash table of the same type (IP Tree

node, Fig. 6).

Figure 6: IPTree general structure.

As in the other ADTs, no repetition of IPs are

allowed. Leaf nodes maintain the information

regarding the IDs of the rules that share a common

value for an IP address selector. In fact, leaf nodes

does not have a hash table for storing <Node octet,

Children octets> (since they do not have any

children), but a hash table with a perfect hash

function (there are only 30 possible CIDRs) to store

<CIDR, RuleID Bit set>. CIDRs represent the

CIDRs of the inserted rules that ended in that leaf,

and if there are many with same CIDR (i.e. a

repeated value), then bits are set to ‘1’ in the bit set.

Insertions are done traversing the tree from top to

bottom. First, the IP/CIDR address to be inserted is

decomposed in its four natural octets plus the CIDR

value: o1.o2.o3.o4/cidr. Then, the root node hash

table is asked in order to know if o1 is already in the

first level of the IP Tree. If it is, the next step is to

navigate to the second level through the found octet

(using the children hash table). If not, a new IP Tree

node with value o1 is inserted in the root node

children hash table. These same is done for o2, o3,

and o4. Once at the last level, if o4 has been found, a

check is launched for the CIDR data stored in the

leaf <CIDR, Rule ID Bit set> hash table using cidr

value of the IP. If cidr value is found, the bit

corresponding to the ID of the inserted IP is set to

‘1’. If not, a new CIDR value is created with its

corresponding bit set. Thus, the insertion of a new IP

consists, in the worst case, of three O(1) searches in

perfect hash tables, plus a O(1) search in a leaf

perfect hash table, resulting in O(1) worst case time

complexity.

The search operation follows the same scheme as

the insertion one. Note that in order to know if two

IP addresses intersect, the application of the shortest

netmask of the two IP addresses is necessary, as has

been pointed at the beginning of the subsection.

However the result we need is the intersection of one

IP with all IPs in the IP Tree, which contains all the

IPs of the m rules in ACL

allow

. Thus, the application

of all netmasks of the IPs in the IP Tree which are

smaller than or equal the CIDR of the given R

address is necessary (at most 30 netmasks). The

result of the application of these netmasks is a set of

(at most) 30 network IPs. Now, a search operation

for each of these IPs is launched. The search

operation follows the same algorithm used for

insertions, but taking the list of rule IDs associated

to the CIDR of the leaf which coincide with the

CIDR used for the search, if a search ends

successfully. The result of the search operation is the

union of all bit sets associated to IP addresses in the

IP Tree which intersect the given IP address of R

(e.g. the result of the –at most- 30 searches), or a bit

set with all bits set to ‘1’ if the given IP address of

is ‘*’. Note that having 30 different netmaks in a

real firewall ACL is not very usual, because this

usually indicates that the firewall is controlling

traffic between 30 different networks, each one

attached to a different physical network interface.

Thus, worst case time complexity of a search

operation of a network address in a network tree is

in O(30*(4*1+1))=O(1). However, in the average

EFFICIENT ALGORITHMS AND ABSTRACT DATA TYPES FOR LOCAL INCONSISTENCY ISOLATION IN

FIREWALL ACLS

Figure 7: IPTree example for network addresses.

case, the multiplicative factor 30 of one search

operation can be reduced to 30-h. If a search

operation successfully ended in a leaf l, and l

contains k CIDR values not yet used for a search in

the IPTree list of CIDRs, then these values should

not be used, because if used for searches, they will

lead to the same leaf l, causing a duplicate search.

This reduction of CIDRs can be made each time a

new leaf is visited, thus the sum of these removed

CIDRs is h.

Finally, host search is slightly different. Suppose

that the search operation receives a host IP address

from R

. In this case, all CIDRs of the IP tree must

be applied to the host IP, creating at most 30 IP

network address. If the IP tree only contains network

IP addresses, the procedure is the described above

with no modifications at all. However, if the IP Tree

also has host IP addresses, the new network address

created from the application of a CIDR to the host IP

address of R

, could also intersect with another host

IP address of the IP tree. This is an important

problem, because the IP address of R

cannot

intersect with more than one host IP address of the

tree (the one that is exactly equal to the IP of R

although it can intersect with many network IP

addresses. This multiple host IP intersection problem

can be solved splitting the IP Tree in two disjoint IP

trees: one to store network ACL

allow

IP addresses and

wildcards, and another one to store ACL

allow

host IP

addresses. The network IP Tree is exactly the

described one (Figs. 6 and 7), but the host IP Tree is

a simplified version, where no CIDR information is

stored in leaves, and where all searches are exact

1..1. In addition, a slightly simplified version of

insert and search methods are necessary for the host

IP Tree. These simplifications are not described here

due to space constraints, but could easily be derived.

4.4 Combination of Search Results

Using the calculated worst case time complexities of

the search operations for the five selectors and, by

the sum of the rule, the combined search time for

five selectors is in worst case

O(1+2*1+2*logm)=O(logm). The first factor is the

time associated to the hash table search (used by

protocol number selector), the second is the two

searches in IP Trees (used by source and destination

IP address selectors), and the last one is the two

searches in interval trees (used by source and

destination port selectors).

The obtained results are five bit sets with

positions set to ‘1’ for intersecting rule IDs.

However, from the inconsistency definitions, all

selectors must overlap for a rule to be inconsistent

with other(s). Thus, the composition of this result is

somewhat trivial: the intersection of the five bit sets.

This intersection gives all between

ddeny

RACL∈ and

all rules in ACL

allow

. This result can directly be used

by the firewall administrator, since no

decomposition has been made to the firewall ACL.

Fig. 8 is an example for

0 deny

RACL∈ , where the

five bit sets resulting from the five searches for R

selectors and their intersection are shown. Some of

these results have been presented in previous

figures. In this case the combination step is

necessary because all searches have returned non-

empty bit sets. The returned bit set indicates that R

is inconsistent with R

and R

. Now is the firewall

SECRYPT 2009 - International Conference on Security and Cryptography

administrator who decides if these two

inconsistencies are faults or not.

SrcIP 1 1 1 1 1 1 0

DstIP 1 1 1 1 1 1 1

SrcPort 1 1 1 1 1 1 1

DstPort 1 1 0 0 0 0 1

Protocol 1 1 1 1 0 0 0

Combination 1 1 0 0 0 0 0

Figure 8: Combination step example.

As its name indicates, a bit set is an ADT whose

main purpose is to store bit elements. The

intersection of the five bit sets is a linear time

operation with the size of the bit sets (or the number

of rules in the ADTs, m, reduced by a constant factor

derived from the duplicate removals). However, in

the worst case, no repetitions are considered. Note

that although the problem is linear, logical

operations over bit arrays are very efficient, as they

are instructions that can be executed in one machine

cycle over 128 bit registers (at least) using special

multi-register multimedia instructions. This yields a

severe problem reduction by a big constant, k≥128,

in time (with no space penalty).

Thus, worst case time complexity of the full

process (for the n rules in ACL

deny

), including the

combination operation, is in worst case O(n*(logm +

m/k), n=m=f/2, m/k>logm

O(n*logm)+O(n*m/k)

O(f/2*log(f/2))+O(f/2*(f/2)/k),(f/2)/k>log(f/2)

O(f/2*(f/2)/k)

O((f

/2)/2k)

O(f

/4k), k≥128.

Derived from this analysis is the fact the

complexity is bounded principally by the number of

allow and deny rules (if they are equal, n=m=f/2,

worst case is achieved). However, as it is going to be

shown in the experimental results, worst case ACLs

are really unusual in the real word, where firewalls

usually control traffic between small network

segments with very specific services, and where

multiple firewall configurations are the norm. Thus,

best and average cases are achieved when there a lot

of selector repetitions in ACL

allow

(and thus ADTs

are very small), when n<<m, and when ACL

consistent (if a selector of a rule of ACL

deny

consistent with the same selector of all the rules of

ACL

allow

, then that rule of ACL

deny

is consistent by

definition, no more searches for the rest of selectors

are needed, and thus no combination of search

results is needed). This results in O(n*logm), where

m is very small due to duplicates

O(n), n<<m.

As has also been shown, the space needed in the

process is linear with the number of rules in ACL

allow

plus some bit sets (the space needed to store the bit

sets is negligible).

As the experimental results will show, this

complexity represents (for the tested real ACLs

(average cases) an algorithm that is up to three

orders of magnitude faster than the trivial O(f

), and

one to two orders faster than (Baboescu, 2003),

which is the best known algorithm to date.

Unfortunately, a direct theoretical comparison with

Baboescu ASBV algorithm is not possible, since its

time complexity is provided in number of memory

accesses. The complexity reduction of our algorithm

in the worst case is mainly obtained from the big

multiplicative constant, k, and in the best case is

mainly obtained from the ADTs.

5 EXPERIMENTAL RESULTS

In absence of standard ACLs or synthetic ACL

generators, the algorithms have been tested with real

firewall ACLs (Table 1).

The conducted performance analysis represents a

wide spectrum of cases, with ACLs of sizes ranging

from 50 to 10600 rules, and percentages of allow

and deny rules ranging from 2% to 65%. Recall that

worst case for our proposal is achieved when half

rules are allow and the other half are deny, and

where all rules are inconsistent. Also note that real

ACLs have some important differences with

synthetically generated ones. The most important

one is the number of deny and allow rules: as real

firewall ACLs are usually designed with deny all

default policy, most rules are going to have allow

actions, and thus ACL

allow

will be bigger than

ACL

deny

. The result is that the worst case would not

normally be achieved in real firewall ACLs.

Experiments were performed on a monothreaded

Java implementation with Sun JDK 1.6.0 64-Bit

Server VM, on an isolated HP Proliant 145G2

(AMD Opteron 275 2.2GHz, 2Gb RAM DDR400).

Execution times are in milliseconds.

As is shown in Table 1, execution of the isolation

process (for all rules in ACL

deny

) is really fast, even

in large ACLs. If the difference between the trivial

algorithm and the optimized version proposed in

(Pozo2, 2008) is very big, the difference between the

trivial one and the proposed in this paper is

dramatic, with improvements of up to x3000 for the

trivial, and up to x60 for the optimized trivial (with

the test ACLs).

In the case of Baboescu ASBV algorithm, results

show that his algorithm is 30 times faster than the

trivial one, which also coincide with the conclusions

EFFICIENT ALGORITHMS AND ABSTRACT DATA TYPES FOR LOCAL INCONSISTENCY ISOLATION IN

FIREWALL ACLS

Table 1: Performance evaluation.

ACL

Size

%Deny

Rules

No.

Inconsist

Trivial

Isolation

(ms)

Optimized Trivial

Isolation Algorithm

(ms)

Baboescu

Isolation

Algorithm (ms)

Proposed Isolation

Algorithm (ms)

ADT

build (ms)

50 28,21 37 0.22 0.09 0.58 0.03 0.09

144 30,91 108 1.34 0.62 1.50 0.06 0.17

238 66,43 231 3.56 2.04 2.71 0.17 0.22

450 34,73 422 13.22 5.61 5.29 0.26 0.54

900 14,8 871 51.57 3.46 11.11 0.4 1.14

2500 6,97 3349 387.86 55.01 43.12 0.86 3.54

5000 1,98 4937 3160.09 64.33 106.99 1.06 9.02

10611 2,05 11866 12046.67 332.85 476.81 8.31 21.85

Table 2: Number of different elements per selector and per ACL.

ACL

Size

Protocol

Hash Table

size

Source Port

ITree size

Dst Port

ITree size

SrcIP Host IP

Tree size

SrcIP NW IP

Tree size

DstIP Host IP

Tree size

DstIP NW IP

Tree size

39 34 4928 2

110 3 11 11 18 4 27 4

143 3 14 17 20 4 30 4

334 3 19 26 29 4 38 4

784 3 19 31 31 4 47 4

2337 3 47 49 76 5 70 5

4903 2 45 50 136 10 142 10

10398 3 86 87 177 25 217 25

Our proposal represents a 10 to 100 times faster

alternative than the current best known one. This

represents a dramatic improvement over other

proposals, specially taken into account that our

algorithm returns results the isolation over the

original, unmodified, ACL, and not over a pre-

processed one (as Baboescu proposal does).

Figure 9 presents a graphic comparison between

the optimized trivial (Pozo2, 2008), Baboescu

ASBV (Baboescu, 2003), and our new algorithms.

The last column in Table 1 presents ADT build

time for all ADTs, showing that they are very

reasonable and amortizable in a few worst-case

searches. Note that once ADTs are built, they need

no modification (unless the ACL changes).

The number of different values per selector and

per ACL is presented in Table 2. Note that if there

are a lot of values of selectors repeated in different

rules of the same ACL, then search times severely

improve. This is especially important for the two

port selectors, since the Interval Tree is the ADT

which has the worst time complexity of all ADTs.

As can be seen in Table 2, the number of repetitions

in the values of the selectors is unsurprisingly high

in real ACLs, even if they are very big. With

sufficiently small ADTs, experimental search times

are near constant (this fact can be seen in Table 1, in

the proposed algorithm column). The algorithms

scale very well. This confirms our assumptions over

real ACLs made at the end of the previous section.

Figure 9: Execution times.

6 CONCLUSIONS

During firewall ACL design and management

inconsistencies can be introduced. An inconsistent

firewall ACL implies in general a design error.

SECRYPT 2009 - International Conference on Security and Cryptography

However, the firewall administrator is who

ultimately decides if an inconsistent rule is faulty.

In this paper, we have proposed a new

inconsistency isolation algorithm for firewalls with

five integer (or intervals of integer). Our approach

has been based on an analysis of which data type

each rule selector can to store, on the design of

specialized abstract data types for each one, and on

divide and conquer algorithm. A theoretical

algorithmic complexity as well as an experimental

performance analysis has been made in order to

validate our theoretical results.

Our proposal represents an algorithm that is 10 to

100 times faster then the current best known one.

Furthermore, results are returned over the original,

unmodified ACL in our case, rather than over a

decomposed ACL which is different than the

original one.

However, our approach has some limitations that

give us opportunities for improvement in future

works. A performance analysis of each part ADT of

the algorithm is necessary in order to know where

the bottleneck is now, in order improve even more

the algorithms. Checking the behaviour of the

proposed ADTs in dynamic environments could be

another interesting point, where another comparison

in complexity and memory requirements to

Baboescu algorithm would be a point.

ACKNOWLEDGEMENTS

This work has been partially funded by Spanish

Ministry of Science and Education project under

grant DPI2006-15476-C02-01, and by FEDER

(under ERDF Program).

REFERENCES

Al-Shaer, E., Hamed, H. Modeling and Management of

Firewall Policies. IEEE eTransactions on Network and

Service Management (eTNSM) Vol.1, No.1, 2004.

Baboescu, F., Varguese, G. Fast and Scalable Conflict

Detection for Packet Classifiers. Computers & Networks

Vol.42, No.6, Elsevier 2003.

Bollig, B., Wegener, I. Improving the Variable Ordering of

OBDDs is NP-Complete. IEEE Transactions on

Computers, Vol.45 No.9, September 1996.

Cormen, T., Leiserson, C., Rivest, R., Stein, C. Introduction

to Algorithms, 2nd Ed. McGraw-Hill, 2001.

Chiang, Y., Tamassia, R. Dynamic Algorithms in

Computational Geometry. Technical Report CS-91-24.

Brown University, Providence, RI, USA, 1991.

de Berg, M., van Kreveld, M., Overmars, M., Schwarzkopf,

O. Computational Geometry: Algorithms and

Applications. Springer-Verlag, Berling, 1997.

Edelsbrunner, H. A new approach to rectangle intersections,

Part II. International Journal on Computational

Mathematics. Vol.13, pp. 221-229, 1983.

Edelsbrunner2, H. A new approach to rectangle intersections,

Part I. International Journal on Computational

Mathematics. Vol.13, pp. 209-219, 1983.

Eppstein, D., Muthukrishnan, S. Internet Packet Filter

Management and Rectangle Geometry. Proceedings of

the Annual ACM-SIAM Symposium on Discrete

Algorithms (SODA), January 2001.

García-Alfaro, J., Boulahia-Cuppens, N., Cuppens, F.

Complete Analysis of Configuration Rules to Guarantee

Reliable Network Security Policies, Springer-Verlag

International Journal of Information Security. Vol.7,

No.2, 2008.

Gupta, P., McKcown, N. Packet classification on multiple

fields. Proceedings of the ACM SIGCOMM. Cambridge,

MA, USA. September 1999.

Hamed, H., Al-Shaer, E. Taxonomy of Conflicts in Network

Security Policies. IEEE Communications Magazine

Vol.44, No.3, 2006.

Hari, B., Suri, S., Parulkar, G. Detecting and Resolving

Packet Filter Conflicts. Proceedings of IEEE INFOCOM,

March 2000.

Liu, Alex X., Gouda, Mohamed G., "Complete Redundancy

Removal for Packet Classifiers in TCAMs," IEEE

Transactions on Parallel and Distributed Systems, 24

Sept. 2008. IEEE computer Society Digital Library. IEEE

Computer Society.

Luis, S., Condell, M. Security policy protocol. IETF Internet

Draft IPSPSPP-01, 2002.

Pozo1, S., Ceballos, R., Gasca, R.M. Model Based

Development of Firewall Rule Sets: Diagnosing Model

Faults. Information and Software Technology Journal,

No. 51, Issue 5, pp. 894-915. Elsevier, 2009.

Pozo2, S., Ceballos, R., Gasca, R.M.. A Heuristic Polynomial

Algorithm for Local Inconsistecy Diagnosis in Firewall

Rule Sets. 3rd International Conference on Security and

Cryptography (SECRYPT), in International Conference

on e-Business and Telecommunications (ICETE). Porto,

Portugal. INSTICC Press, 2008.

Srinivasan, V., Varguese, G, Suri, S., Waldvogel, M. Fast and

Scalable Layer Four Switching. Proceedings of the ACM

SIGCOMM conference on Applications, Technologies,

Architectures and Protocols for Computer

Communication, Vancouver, British Columbia, Canada,

ACM Press, 1998.

Taylor, David E. Survey and taxonomy of packet

classification techniques. ACM Computing Surveys,

Vol.37, No.3, 2005.

Wool, A. A quantitative study of firewall configuration errors.

IEEE Computer, Vol.37, No.6, 2004.

Yuan, L., Mai, J., Su, Z., Chen, H., Chuah,, C. Mohapatra, P.

FIREMAN: A Toolkit for FIREwall Modelling and

ANalysis. IEEE Symposium on Security and Privacy

(S&P’06). Oakland, CA, USA. May 2006.

EFFICIENT ALGORITHMS AND ABSTRACT DATA TYPES FOR LOCAL INCONSISTENCY ISOLATION IN

FIREWALL ACLS