
TOWARD A SEMI-SUPERVISED APPROACH IN
CLASSIFICATION BASED ON PRINCIPAL DIRECTIONS
Luminita State
Dept. of Computer Science, University of Pitesti
Caderea Bastliei #45, Bucuresti – 1, Pitesti,Romania
Catalina Cocianu
Dept. of Computer Science, Academy of Economic Studies
Calea Dorobantilor #15-17, Bucuresti –1, Bucharest, Romania
Doru Constantin, Corina Sararu
Dept. of Computer Science, University of Pitesti, Pitesti, Romania
Panayiotis Vlamos
Ionian University, Corfu, Greece
Keywords: Principal component analysis, Data compression/decompression, Statistical signal classification, First order
approximation for eigen values and eigen vectors.
Abstract: Since similarity plays a key role for both clustering and classification purposes, the problem of finding a
relevant indicators to measure the similarity between two patterns drawn from the same feature space
became of major importance. The advantages of using principal components reside from the fact that bands
are uncorrelated and no information contained in one band can be predicted by the knowledge of the other
bands. The semi-supervised learning (SSL) problem has recently drawn large attention in the machine
learning community, mainly due to its significant importance in practical applications. The aims of the
research reported in this paper are to report experimentally derived conclusions on the performance of a
PCA-based supervised technique in a semi-supervised environment. A series of conclusions experimentally
established by tests performed on samples of signals coming from two classes are exposed in the final
section of the paper.
1 INTRODUCTION
In supervised learning, the basis is represented by a
training set of examples (inputs) with associated
labels (output values). Usually, the examples are in
the form of attribute vectors, so that the input space
is a subset of R
n
. Once the attribute vectors are
available, a number of sets of hypothesis could be
chosen for the problem.
Traditional statistics and the classical neural
network literature have developed many methods for
discriminating between two classes of instances
using linear functions, as well as methods for
interpolation using linear functions. These
techniques, which include both efficient iterative
procedures and theoretical analysis of their
generalization properties, provide a suitable
framework within which the construction of more
complex systems are usually developed.
The semi-supervised learning (SSL) problem has
recently drawn large attention in the machine
learning community, mainly due to its significant
importance in practical applications.
In statistical machine learning, there is a sharp
distinction between unsupervised and supervised
learning. In the former scenario we are given a
68
State L., Cocianu C., Constantin D., Sararu C. and Vlamos P. (2009).
TOWARD A SEMI-SUPERVISED APPROACH IN CLASSIFICATION BASED ON PRINCIPAL DIRECTIONS.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 68-73
DOI: 10.5220/0002233200680073
Copyright
c
SciTePress

sample
{}
i
x of patterns in ℵ drawn independently
and identically distributed (i.i.d.) from some
unknown data distribution with density P(x), the
goal being to estimate either the density or a
functional thereof. Supervised learning consists of
estimating a functional relationship x → y between a
covariate
ℵ∈x and a class variable
{}
My ,...,2,1∈ ,
with the goal of minimizing a functional of the joint
data distribution P(x, y) such
as the probability of classification error.
The terminology “unsupervised learning” is a bit
unfortunate: the term density estimation should
probably suit better. Traditionally, many techniques
for density estimation propose a latent (unobserved)
class variable y and estimate P(x) as
mixture distribution
()
()
∑
=
M
y
yPyxP
1
. Note that y has
a fundamentally different role than in classification,
in that its existence and range c is a modeling choice
rather than observable reality.
The semi-supervised learning problem belongs to
the supervised category, since the goal is to
minimize the classification error, and an estimate of
P(x) is not sought after. The difference from a
standard classification setting is that along with a
labeled sample
()
{
}
niyxD
iil
,...,1, == drawn i.i.d.
from P(x, y) we also have access to an additional
unlabeled sample
{
}
mjxD
jnu
,...,1==
+
from the
marginal P(x). We are especially interested in cases
where n«m which may arise in situations where
obtaining an unlabeled sample is cheap and easy,
while labeling the sample is expensive or difficult.
Principal Component Analysis, also called
Karhunen-Loeve transform is a well-known
statistical method for feature extraction, data
compression and multivariate data projection and so
far it has been broadly used in a large series of signal
and image processing, pattern recognition and data
analysis applications.
The advantages of using principal components
reside from the fact that bands are uncorrelated and
no information contained in one band can be
predicted by the knowledge of the other bands,
therefore the information contained by each band is
maximum for the whole set of bits (Diamantaras,
1996).
Recently, alternative methods as discriminant
common vectors, neighborhood components analysis
and Laplacianfaces have been proposed allowing the
learning of linear projection matrices for
dimensionality reduction. (Liu, Chen, 2006;
Goldberger, Roweis, Hinton, Salakhutdinov, 2004)
The aims of the research reported in this paper
are to report experimentally derived conclusions on
the performance of a PCA-based supervised
technique in a semi-supervised environment.
The structure of a class is represented in terms
of the estimates of its principal directions computed
from data, the overall dissimilarity of a particular
object with a given class being given by the
“disturbance” of the structure, when the object is
identified as a member of this class. In case of
unsupervised framework, the clusters are computed
using the estimates of the principal directions, that is
the clusters are represented in terms of skeletons
given by sets of orthogonal and unit eigen vectors
(principal directions) of each cluster sample
covariance matrix. The reason for adopting this
representation relies on the property that a set of
principal directions corresponds to the maximum
variability of each class.
A series of conclusions experimentally
established by tests performed on samples of signals
coming from two classes are exposed in the final
section of the paper.
2 THE MATHEMATICS BEHIND
THE PROPOSED ATTEMPT
The classes are represented in terms of multivariate
density functions, and an object coming from a
certain class is modeled as a random vector whose
repartition has the density function corresponding to
this class. In cases when there is no statistical
information concerning the set of density functions
corresponding to the classes involved in the
recognition process, usually estimates based on the
information extracted from available data are used
instead.
The principal directions of a class are given by a
set of unit orthogonal eigen vectors of the
covariance matrix. When the available data is
represented by a set of objects
N
XXX ,...,,
21
,
belonging to a certain class C, the covariance matrix
is estimated by the sample covariance matrix,
()()
∑
=
−−
−
=Σ
N
i
T
NiNiN
XX
N
1
ˆˆ
1
1
ˆ
μμ
, (1)
where
∑
=
=
N
i
iN
X
N
1
1
ˆ
μ
.
Let us denote by
N
n
NN
λλλ
≥≥≥ ...
21
the eigen
values and by
N
n
N
ψψ ,...,
1
a set of orthonormal
eigen vectors of
N
Σ
ˆ
.
TOWARD A SEMI-SUPERVISED APPROACH IN CLASSIFICATION BASED ON PRINCIPAL DIRECTIONS
69

If a new example X
N+1
coming from the same
class has to be included in the sample, the new
estimate of the covariance matrix can be recomputed
as,
()()
111
1
ˆˆ
ˆˆ
1
T
NN NNNN
N
μ
+++
=+ − − −
+
ΣΣ X μ X
1
ˆ
N
N
−Σ
(2)
Using first order approximations (State, Cocianu,
2006), the estimates of the eigen values and eigen
vectors respectively are given by,
() ()
N
iN
T
N
i
N
iN
T
N
i
N
i
N
i
ψΣψψΣψ
1
1
ˆˆ
+
+
=Δ+=
λλ
(3)
()
∑
≠
=
+
−
Δ
+=
n
ij
j
N
j
N
j
N
i
N
iN
T
j
N
N
i
N
i
1
1
ˆ
ψ
ψΣψ
ψψ
λλ
(4)
On the other hand, when an object has to be
removed from the sample, then the estimate of the
covariance matrix can be computed as,
11
ˆˆ
++
Δ+=
NNN
ΣΣΣ , (5)
where
()()
()()
11
11
1
ˆ
1
11
NN
T
NNNN
N
N
NN
++
++
Δ= −
−
−−−
−+
ΣΣ
X μ X μ
and
()
N
N
N
NN
N
11
1
++
−
+
=
Xμ
μ
The conclusion formulated in the next lemma
can be proved by straightforward computation.
Lemma. Let
K
XXX ,...,,
21
be an n-dimensional
Bernoullian sample. We denote by
,
1
ˆ
1
∑
=
=
N
i
iN
N
Xμ
()()
∑
=
−−
−
=
N
i
T
NiNiN
N
1
ˆˆ
1
1
ˆ
μXμXΣ
, and let
{
}
ni
N
i
≤≤1
λ
be the eigen values and
{
}
ni
N
i
≤≤1
ψ a set of
orthogonal unit eigen vectors of
N
Σ
ˆ
,
12 −≤≤ KN . In case the eigen values of
1
ˆ
+N
Σ are
pairwise distinct, the following first order
approximations hold,
()
1
1
11 +
+
++
Δ+=
N
iN
T
N
i
N
i
N
i
ψΣψ
λλ
(6)
()
∑
≠
=
+
++
+
+
+
+
−
Δ
+=
n
ij
j
N
j
N
j
N
i
N
iN
T
N
j
N
i
N
i
1
1
11
1
1
1
1
ψ
ψΣψ
ψψ
λλ
(7)
where
11
ˆˆ
++
−=Δ
NNN
ΣΣΣ
Let
N
n
N
ψψ
,...,
1
be set of principal directions of
the class C computed using
N
Σ
ˆ
. When the example
X
N+1
is identified as a member of the class C, then
the disturbance implied by extending C is expressed
as,
(
)
∑
=
+
=
n
k
N
k
N
k
d
n
D
1
1
,
1
ψψ
(8)
where d is the Euclidian distance and
11
1
,...,
++ N
n
N
ψψ
are the principal directions computed using
1
ˆ
+N
Σ .
Let
{
}
M
CCCH ,...,,
21
=
be a set of classes,
where the class C
j
contens N
j
elements. The new
object X is alloted to C
j
, one of the classes for which
(
)
==
∑
=
+
n
k
N
jk
N
jk
jj
d
n
D
1
1
,,
,
1
ψψ
(
)
∑
=
+
≤≤
=
n
k
N
pk
N
pk
Mp
pp
d
n
1
1
,,
1
,
1
min
ψψ
(9)
In order to protect against misclassifications, due
to insufficient “closeness” to any class, we
implement this recognition technique using a
threshold T>0 such that the example
X is allotted to
C
j
only if relation (8) holds and D<T.
The classification of samples for which the
resulted value of D is larger than T is postponed and
the samples are kept in a new possible class CR. The
reclassification of elements of CR is then performed
followed by the decision concerning to either
reconfigure the class system or to add CR as a new
class in H.
For each new sample allotted to a class, the class
characteristics (the covariance matrix and the
principal axes) are re-computed using (2), (3) and
(4). The skeleton of each class is computed using an
exact method,
M, in case PN samples have been
already classified in
{
}
M
CCCH ,...,,
21
=
.
Briefly, the recognition procedure, P1, is
described below (Cocianu, State, 2007).
Input:
{
}
M
CCCH ,...,,
21
=
the set of samples
coming from M classes respectively
Step 1: For each class, compute a set of
orthogonal unit eigen vectors (characteristics of the
classes)
Repeat
i←1
Step 2: Generate X a new test example and
classify
X according to (8)
Step 3: If Mjj
≤
≤
∃
1, such that X is allotted
to
j
C , then
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
70

3.1.re-compute the characteristics of
j
C using
(3), (4) and (5)
3.2. i←i+1
Step 4: If i<PN goto Step 2
Else
4.1. For i=
M,1 , compute the characteristics
of the class
i
C using M. 4.2. goto Step 2.
Until all test examples are classified
Output
: The new set
{}
CRCCC
M
∪,...,,
21
3 EXPERIMENTAL ANALYSIS
ON THE PERFORMANCE OF
THE PROPOSED
CLASSIFICATION METHOD
In this section, we present the results in testing the
performance of the proposed approach evaluated in
terms of the recognition error. The tests were
performed in discriminating between two classes of
signals, with known statistical properties. The
evaluation of the error is computed on new test
examples. The approach can be taken as a semi-
supervised approach because each new test example
is included in the class established by the decision
rule (not necessarily being the true provenance class)
therefore becoming involved in the re-actualization
of the new characteristics.
The classes are represented by NP examples
coming from each class.
Test 1. The evaluation of error using the leaving one
out method. Sequentially, one of the given examples
is removed from the sample. The classifier is
designed using the rest of 2NP-1 examples (that is
the characteristics of the classes are computed in
terms of the NP, NP-1 remaining examples) and the
removed example is classified into one of resulted
classes. The error is evaluated as
NP
F
2
, where F is
the number of misclassified examples.
Let
{
}
{
}
ni
NP
i
ni
NP
i
≤≤≤≤ 1
,2
1
,1
,
ψψ
,
{
}
{
}
ni
NP
i
ni
NP
i
≤≤≤≤ 1
,2
1
,1
,
λλ
be the characteristics of the
classes and the corresponding eigen values at the
initial moment and
21
,
NPNP
μμ
,
21
,
NPNP
ΣΣ
the sample
means and the sample covariance matrices
respectivelly. Let X be the removed example. In
case X comes from the first class, then the new
characteristics are,
(
)
∑
≠
=
−
−
ΔΣ
+=
n
ij
j
NP
j
NP
j
NP
i
NP
i
NP
T
NP
j
NP
i
NP
i
1
,1
,1,1
,11,1
,11,1
ψ
λλ
ψψ
ψψ
for the first class and remains unchanged for the
second one, where
()
()()
11
2
1
2
1
1
1
1
1
1
1
1
1
1
11
1
1
−
−
−
=
−−
−
−
−
−Σ
−
−
=Σ
Σ−Σ=ΔΣ
−
−−
−
−
NP
X
NP
NP
XX
NPNP
NP
NP
NP
NP
NP
T
NPNP
NPNP
NPNPNP
μ
μ
μμ
In case X comes from the second class, similar
formula are used.
The evaluation of the error is performed for
50,40,30,20,10
=
NP . Several tests were performed
on samples generated from 3 repartitions, Gaussian,
Rayleigh and geometric, each class corresponding to
one of them. All tests reported to a surprising
conclusion, that is the misclassification error is very
closed to 0.
a) The classes correspond to the Gaussian
repartition and Rayleigh repartition respectively,
NP=150, n=50, e=50, where n is the data
dimensionality and e is the number of epochs, the
resulted empirical error is 0.0327. The variation of
the empirical error in terms of e is presented in
Figure 1.
b) The classes correspond to the geometric
repartition and Rayleigh repartition respectively,
NP=150, n=50, e=50, where n is the data
dimensionality and e is the number of epochs, the
resulted empirical error is 0.0112. The variation of
the empirical error in terms of e is presented in
Figure 2.
Figure 1.
TOWARD A SEMI-SUPERVISED APPROACH IN CLASSIFICATION BASED ON PRINCIPAL DIRECTIONS
71
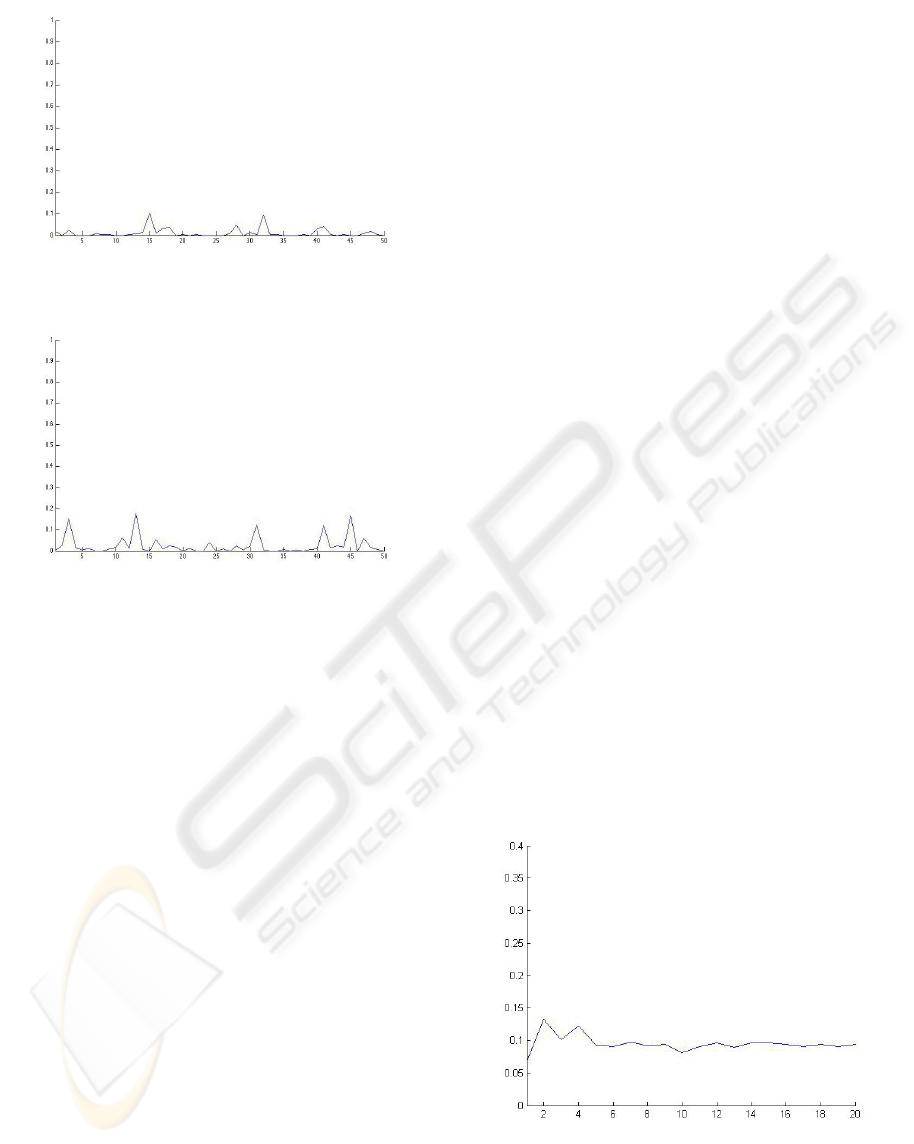
Figure 2.
Figure 3.
c)
The classes correspond to the Gaussian
repartition, NP=150, n=50, e=50, where n is the data
dimensionality and e is the number of epochs, the
resulted empirical error is 0.0261. The variation of
the empirical error in terms of e is presented in
Figure 3.
Test 2.
The evaluation of the error by counting the
misclassified examples from a set of NC new test
samples coming from the given classes of the same
repartitions.
In this case, the learning is performed in a non-
adaptive way, that is first order approximations of
the characteristics for each class are used for
classification purposes only (the characteristics of
the classes are the initial computed characteristics
during the classification process).
The tests were performed for
NP=10,20,30,40,50, NC=10,20,30,40,50, n=50,
e=50, where n is the data dimensionality and e is the
number of epochs.
a) The classes correspond to the Gaussian
repartition and Rayleigh repartition respectively.
b) The classes correspond to the geometric
repartition and Rayleigh repartition respectively.
c) The classes correspond to the Gaussian
repartition.
The values of the empirical error in terms of e lie
in the interval [0.02,0.15] in case a), [0.32,0.4] in
case b), and [0.04,0.4] in case c) respectively. In all
cases, a decreasing tendency is identified while the
number of epochs increases.
Test 3. The evaluation of the error by counting the
misclassified examples from a set of NC new test
samples coming from the given classes of the same
repartitions.
In this case, the learning is performed in an
adaptive way, that is, each new classified example
contributes to the new characteristics of the class the
exampled is assigned to, the new characteristics
being computed using first order approximations in
terms of the previous ones. Besides, after each
iteration, the characteristics of the new resulted
classes are re-computed using an exact method
M.
The tests were performed for NP=150,
NC=10,20,30,40,50, n=50, e=100, where n is the
data dimensionality and e is the number of epochs.
a) The classes correspond to the Gaussian
repartition and Rayleigh repartition respectively,
The empirical error stabilises in few epochs at the
value 0.015 and remains unchanged while the
number of epochs increases.
b) The classes correspond to the geometric
repartition and Rayleigh repartition respectively.
The variation of the empirical error in terms of e is
presented in Figure 4.
c) The classes correspond to the Gaussian
repartition. The variation of the empirical error in
terms of e is presented in Figure 5.
Figure 4.
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
72

Figure 5.
Finally, we conclude that the long series of tests on
the proposed classification procedure pointed out
very good performance in terms of the
misclassification error. In spite of the apparent
complex structure, using first order approximations
for the class characteristics, its complexity
significantly decreases without degrading the
classification accuracy.
REFERENCES
Chapelle, O., Scholkopf, B., Zien, A. (Eds.), 2006. Semi-
Supervised Learning, MIT Press
Cocianu, C., State, L., Rosca, I., Vlamos, P. 2007. A New
Adaptive Classification Scheme Based on Skeleton
Information, Proceedings of 2nd International
Conference on Signal Processing and Multimedia
Applications 2007
Diamantaras, K.I., Kung, S.Y., 1996. Principal
Component Neural Networks: theory and applications,
John Wiley &Sons
Goldberger, J., Roweis, S., Hinton, G., Salakhutdinov, R.,
2004. Neighbourhood Component Analysis. In
Proceedings of the Conference on Advances in Neural
Information Processing Systems
Gordon, A.D. 1999. Classification, Chapman&Hall/CRC,
2
nd
Edition
Hastie, T., Tibshirani, R., Friedman, J. 2001. The Elements
of Statistical Learning Data Mining, Inference, and
Prediction. Springer-Verlag
Jain,A.K., Dubes,R., 1988. Algorithms for Clustering
Data, Prentice Hall,Englewood Cliffs, NJ.
Liu, J., and Chen, S. 2006. Discriminant common vectors
versus neighbourhood components analysis and
Laplacianfaces: A comparative study in small sample
size problem. Image and Vision Computing 24 (2006)
249-262
Smith,S.P., Jain,A.K., 1984. Testing for uniformity in
multidimensional data, In IEEE Trans.`Patt. Anal.`
and Machine Intell., 6(1),73-81
State, L., Cocianu, C., Vlamos, P, Stefanescu, V., 2006.
PCA-Based Data Mining Probabilistic and Fuzzy
Approaches with Applications in Pattern Recognition.
In Proceedings of ICSOFT 2006, Portugal, pp. 55-60
.
Ripley, B.D. 1996. Pattern Recognition and Neural
Networks, Cambridge University Press, Cambridge
TOWARD A SEMI-SUPERVISED APPROACH IN CLASSIFICATION BASED ON PRINCIPAL DIRECTIONS
73
