AD-HOC ON DEMAND AUTHENTICATION CHAIN PROTOCOL

An Authentication Protocol for Ad-hoc Networks

A. M. Hamad

Faculty of Informatics and Computer Sciences, British University in Egypt (BUE), Egypt

W. I. Khedr

Faculty of Computers and Informatics, Zagazig University, Egypt

Keywords: Mobile ad-hoc networks, Authentication, Man-in-the-middle attack, Key establishment, Transitive

authentication.

Abstract: A mobile ad hoc network is an autonomous system that is made up of collaborative mobile nodes. Nodes in

mobile ad hoc networks have limited capabilities and dynamic topology. Authentication of network nodes

and the establishment of secret keys among nodes are both target security objectives in ad hoc networks.

The constrained devices and other special properties of ad hoc networks make achieving those security

properties a challenging task. This paper proposes an authentication protocol, Ad-hoc On Demand

Authentication Chain Protocol (AOAC), which allow individual node to authenticate each other and to

establish a shared key for secure peer-to-peer communication, the authentication does not rely on any

centralize trusted authority or fixed server and is not based on public key cryptography. To provide both

node authentication and pair-wise authenticated key establishment we proposed a transitive authentication

technique by which active attacks, specially the man-in-the-middle attack, can be prevented. The security of

our protocol is analyzed using GNY logic. We also provided simulation and performance analysis of the

proposed authentication protocol.

1 INTRODUCTION

Mobile ad hoc networks are gaining popularity as

these networks are self organizing without requiring

fixed infrastructure such as servers or access points.

The parties involved might not have a common

history. The devices forming an ad-hoc network are

often small and portable. Therefore, they do not

have much memory or computational power and

they are probably not tamper-resistant. Connections

are formed by jumping from point to point via other

peer devices and not through dedicated router

networks. These limitations pose some drastic

demands on authentication protocols (Murthy and

Manoj, 2004).

Authentication service has become a challenging

task in securing ad-hoc networks. Recent research

work has come up with a variety of protocol for

authentication. Most of the existing protocols have

been devised and engineered based on some specific

scenarios. More precisely they are not general

solution rather they are application specific.

Most of authentication techniques are based on

public key cryptography, (Zhou and Haas, 1999),

(Kong et al., 2001), (Narasimha et al., 2003), (Luo et

al., 2002). Although such techniques have become

quite mature and are widely deployed in wired

networks such as the Internet, they usually do not

adapt well to ad hoc networks.

In this paper we proposed an efficient and secure

authentication scheme for ad-hoc networks. The

proposed scheme supports dynamic topology,

limited resources and lack of central management of

ad-hoc networks. The proposed authentication

protocol allow individual node to authenticate each

other and to establish a shared key for secure peer-

to-peer communication, the authentication does not

rely on any centralize trusted authority or fixed

server and is not based on public key cryptography.

To provide both node authentication and pairwise

authenticated key establishment we proposed a

274

M. Hamad A. and I. Khedr W. (2009).

AD-HOC ON DEMAND AUTHENTICATION CHAIN PROTOCOL - An Authentication Protocol for Ad-hoc Networks.

In Proceedings of the International Conference on Security and Cryptography, pages 274-284

DOI: 10.5220/0002235102740284

 SciTePress

transitive authentication technique by which active

attacks, especially the man-in-the-middle attack

(MITM), can be prevented.

The rest of the paper is organized as follows. Section

2 gives a background of our proposed schemes.

Section 3 describes our proposed authentication

scheme. In Section 4 we present the security and

complexity analysis of our proposed schemes.

Finally we draw the conclusion in Section 5.

2 BACKGROUD

AOAC protocol is based on the technique used in

the establishment of the network and groups keys

proposed in (Hamad et al., 2008a). The main idea

that the scheme proposed in (Hamad et al., 2008a) is

based on is that active attacks, like MITM attack,

can not be launched against nodes within the

transmission range of each other. This is true

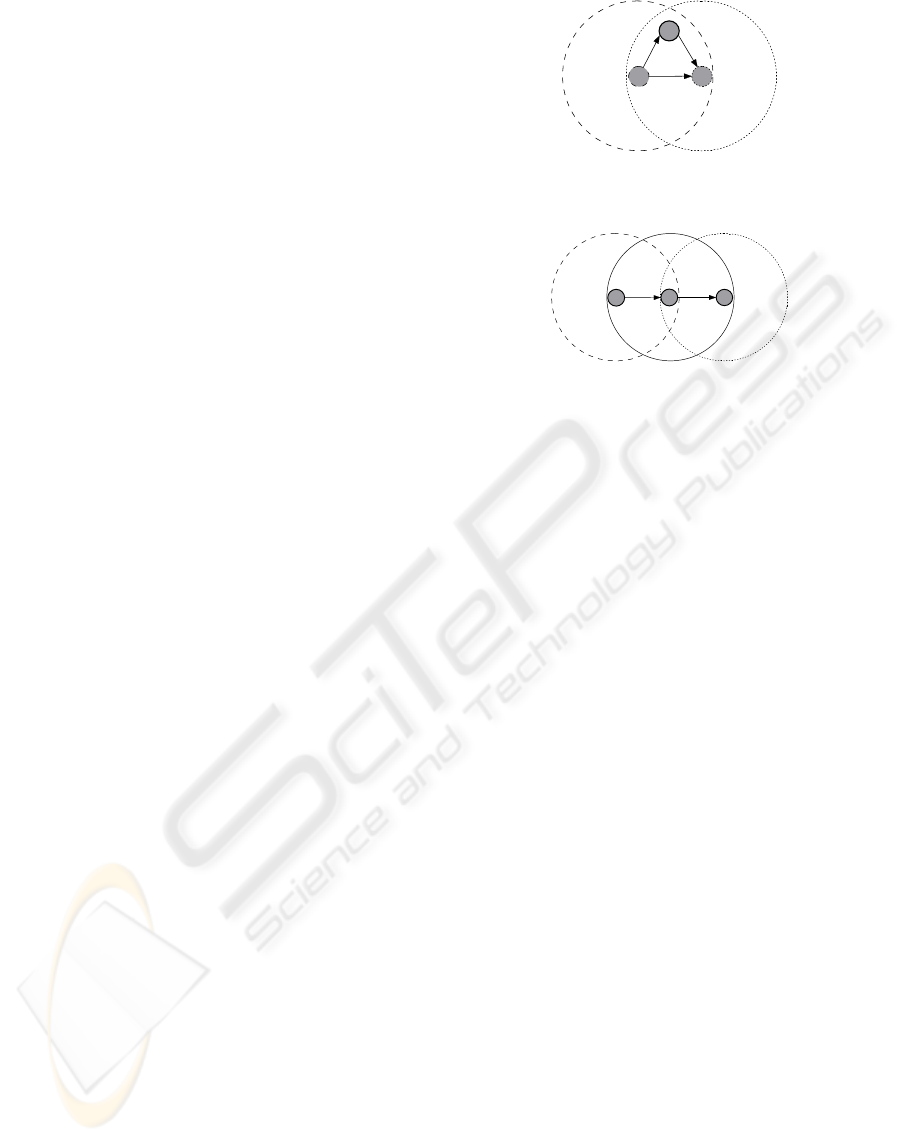
because if node A

sends a message to node B, an

attacker E cannot intercepts the message because the

original message will reach B since it is within A

transmission range, see Figure 1. Active attacks like

MITM attack can be launched against mobile ad-hoc

networks nodes only when any two nodes are out of

the transmission range of each other, so an attacker

can easily intercept a message sent from one node,

modify it and send it to the other node, see

Figure 2.

By the definition of ad-hoc network, during the

formation phase of ad-hoc networks, nodes meet

each other for the first time. So, the main concern in

this phase is how a node can be sure that a message

received from a certain node is really come from that

node and not from another one, we call this message

authentication. Entity authentication in this phase is

not a concern because by the definition of ad-hoc

network, nodes meet each other for the first time in

this phase, so there is no shared key between them

and public keys are not exchanged. So, nodes within

the transmission range of each other can provide

data origin authentication. The scheme we proposed

in (Hamad et al., 2008a) is based on the above

concept; each group of node within the transmission

range of each other starts a key establishment

process.

In this section we give an overview of the key

establishment scheme proposed in (Hamad et al.,

2008a). It is based on both key agreement and key

transport algorithms proposed in (Hamad et al.,

2008b). The protocol is divided into four sub-

protocols.

Figure 1: Node A and B are within the transmission range

of each other.

Figure 2: Node A and B are out of the transmission range

of each other

2.1 The Network Leader Election

Protocol (NLEP)

Each node in the network participates in this

protocol to elect a node that will be the network

leader, R, by locally broadcasting the group of its

direct neighbours that form a complete graph. This

leader should have the maximum number of

immediate neighbours that form a complete graph

i.e. graph with maximum size, , among other nodes.

Nodes apply the algorithm developed by Patric R. J.

Östergård (Östergård, 2002) to calculate the

maximum number of its immediate neighbours that

form a complete graph.

2.2 The Network Leader Confirmation

Protocol (NLCP)

After applying the network leader election protocol,

each node learned the network leader and

max

q nodes. To be sure that the elected node is really

the network leader, other nodes wait for "Root

Confirmation Message" (RCM) from

max

q nodes to

confirm that R belongs to

max

q . We call

max

nodes, excluding R, the "Witness Group" (WG).

2.3 The Network Key Establishment

Protocol (NKEP)

The network leader performs the network key

establishment protocol with WG members to create

the Network Key

K . Since WG members meet

AD-HOC ON DEMAND AUTHENTICATION CHAIN PROTOCOL - An Authentication Protocol for Ad-hoc Networks

275

each other for the first time and since they are within

the transmission range of each other, they use ECBD

key exchange algorithm (Hamad et al., 2008b) to

establish the network key. We call the function that

applies the key exchange algorithm, ECBD, "Key

Exchange Function" (KEF). In NKEP KEF applies

ECBD key exchange algorithm. We assume that a

base point P = (x, y) on elliptic curve in E

(a, b) is

chosen and both E

(a, b) and P are universally

known and used among the network members. We

also assume that each node

N has generated its

elliptic curve DH (ECDH) public and private keys,

KU and

KR respectively. The protocol works

as follows:

1. R finds the set of all cliques in its graph

g ,

{ , ,..., }

RR R

Qqq q= ,

, 1,...,

qi m∈= and

max R

qWGQ=∈,

using the algorithm proposed by Patric R. J.

Östergård (Östergård, 2002).

2. To generate the network key

K , R performs

key establishment between itself and WG

members using ECBD algorithm (Hamad et al.,

2008b).

To distribute the network key to the whole

network, each node should have a shared key with a

group of its immediate neighbours; we call this key

the group key.

2.4 The Groups Key Establishment

Protocol (GKEP)

To propagate the network key to all node, the

network leader has to authenticate it self to the rest

of the network; WG members including R trust each

other because they are within the transmission range

of each other. So, for the rest of nodes to trust R they

should be within its transmission range, but this is

infeasible, so other nodes should inherit this trust

from WG members. This can be done by performing

a key establishment between each member of WG

and its immediate neighbours such that these

neighbours form a complete graph. Using this key

each WG member can propagate the network key to

its immediate neighbours. The protocol assumes that

all nodes do not change their position during the

group key establishment protocol.

The process of propagated group key

establishment starting form R, continue until each

node in the network either belongs to just one group

leaded by a group leader or be a leader of at least

one group which implies that it belongs to a group.

3 AOAC PROTOCOL

AOAC protocol is based on the technique that we

proposed in the establishment of the network and

groups keys, see (Hamad et al., 2008a). It assumes

that the network is partitioned into a set of groups

and each group is leaded by one leader with leaders

connecting these groups. When we say that leaders

connecting groups, we do not mean a physical

connection, we mean an authentication connection

i.e. if node N

connects two group (N

belongs to one

group and leads another one or leads both groups),

then the only way for these two groups to

authenticate each other is through N

; because N

shares a key with the first group and shares another

key with the other group. So, when a source node

wants to authenticate a destination node, it has to

find a set of group leaders that authenticate the

source to destination.

AOAC is a protocol for creating chain of group

leader nodes that authenticate the source node to the

destination node. Also, the created chain will

authenticate the destination node to the source node.

This will be done by constructing a forward path that

authenticate the source node to the destination node

and a reverse path that authenticate the destination

node to source node. We assume that the source and

destination nodes belong to different groups. In case

that the source and destination nodes belong to the

same group (trivial case), they can authenticate each

other through their group leader and their peer-to-

peer session key,

K (A. M. Hamad et al.,

2008b), without using the AOAC as described

below.

Before establishing the Transitive Authentication

Protocol, discussed below, of AOAC protocol, both

the source and the destination nodes should know

the ID and the group ID of each other, we mean by

the group, the group that each of them belongs to,

not they lead. This piece of information (the group

ID) help the AOAC to improve the performance of

the authentication chain discovery protocol as

discussed in the next section. They also should

exchange the ECDH public keys (Hamad et al.,

2008b) of each other, this will prevent the inside

man-in-the-middle attack as discussed later. These

three pieces of information, node ID, group ID and

public key along with a nonce value to prevent

replay attacks, of both the source and destination

nodes should be signed by the network key to

prevent outside MITM attack. AOAC protocol is

divided into two sub-protocols:

SECRYPT 2009 - International Conference on Security and Cryptography

276

• Authentication Chain Discovery Protocol: This

is used to find a chain of leader nodes that

authenticate the source node to the destination

node and vise versa

• Transitive Authentication Protocol: This

protocol allows two nodes to use the

authentication chain to authenticate each other

and to establish a direct pairwise shared key

3.1 Authentication Chain Discovery

Protocol

In this protocol we assume that the group leader ID

is part of the group ID i.e. we can identify the group

leader ID from the group ID, So when the source

node want to find an authentication chain to a

destination node which does not belongs to groups it

leads or belongs to, first it checks if the destination

group leader is one of the leader members of the

groups it leads or belongs to. If it is one of them, it

sends it a "Chain Request (CREQ)", this will save

communication cost; because other nodes are not

able to deliver the request to the destination node,

otherwise the source node sends a (CREQ) to its

group leader and to leader members of the groups it

leads. For example Figure 3 shows the trivial case

when node L4 (leader of group G4) wants to

communicate with node L1 (leader of group G1) and

both nodes belongs to the same group (group G1).

So they can authenticate each other using their

shared session key. Note that gray nodes represent

leader nodes and white nodes represent non-leader

nodes.

In Figure 4, the source node is L4 and the source

group is G1 leaded by L1, the destination node is L8

and the destination group is group G6 leaded by

node L6. As we see L8 neither belongs to group G4,

leaded by L4, nor group G1, but its leader L6

belongs to group G4. So, L4 will forward the CREQ

to leader node L6 and nodes L1, L5, L2, and L3 are

ignored because they are not able to deliver the

CREQ message to L8.

If the source node is the network leader, it sends

the CREQ message to leader members of groups it

leads; this is because the network leader does not

belong to any group (does not have a leader) and set

the source group ID to the witness group ID. When a

node N sends or forwards a CREQ message to a

given node, this node should belongs to groups that

N leads or belongs to. CREQ is also sent to leader

members to save communication cost; because non-

leader members are not able to forward CREQ

message to nodes outside the group it belongs to.

The CREQ message contains the following:

• Source node: this is an ID that uniquely

identifies the source node.

• Source group: the ID of the group that the

source node belongs to.

• Destination node: this is an ID that uniquely

identifies the destination node

• Destination group: the ID of the group that the

destination node belongs to.

• Authenticator count: it is similar to hop count,

it is simply a counter that count the number of

node in the authentication chain

• Sequence Number: Serves as a unique ID of the

CREQ, this sequence number allows nodes to

know which "Chain Reply (CREP)", described

latter, corresponds to a given CREQ.

L10

L11

N5N4

N7N6

L7L8

N11N10

N12

N13

G10

N2N1

G11

Figure 3: L4 and L1 are leader nodes and belong to the

same group (group 1).

L10

L11

N5N4

N7N6

N11N10

N12

N13

G10

N2N1

G11

Figure 4: The destination node L8 neither belongs to

group 4 nor group 1.

3.2 Transitive Authentication Protocol

If the source node

NG∈ wants to

communicate with the destination node

NG∈

1. N

unicasts a communication request message

(MREQ), its ID (N

), group ID (

G ), its

public key

and a nonce value

r signed

AD-HOC ON DEMAND AUTHENTICATION CHAIN PROTOCOL - An Authentication Protocol for Ad-hoc Networks

277

K i.e.

({,,,})

ip Ni

Sign MREQ N G KU r , to

2. When N

receives a MREQ from N

it extracts

the data from the message and store it then send

a communication reply message (MREP),

({,,,})

jv N j

Sign MREP N G KU r

signed by

K to N

and wait for

Authentication Request Message (AREQ),

explained later, from one of leader members

that belongs to

G or belongs to one of groups

it leads. AREQ message has the following

fields:

1. The source node ID

2. The source group ID.

3. The destination node ID

4. The destination group ID.

5. The hash value of the Session Key (KS)

generated by the two parties Elliptic Curve

Diffie-Hellman (ECDH) group key

agreement using the source and destination

node's public key

KU and

KU that

and N

extract from the MREQ and

MREP respectively along with the nonce

value

r + to prevent replay attack. This

key is used for authentication between the

source and destination node and for peer-

to-peer communication between the source

and destination if needed.

3. Node N

applies the "Ad-hoc On-Demand

Authentication Chain (AOAC)" described

above, to find an "Authentication Chain (AC)"

to N

. The authentication chain is a set of group

leader nodes that authenticate the source node to

the leader of the destination group or to a leader

member leaded by the destination node which

authenticate the source node to the destination

node. Also, the created chain will authenticate

the destination node to the source node.

4. Node N

search its authentication chain table for

an authentication chain to the destination group

then sends an Authentication Request (AREQ)

message to the first member of the

authentication chain,

h , pointed to by "Next

Leader" field in its authentication chain table.

This message is signed by the common group

key between itself and h

. The first member of

the authentication chain should be one of the

following:

i. A member of a group leaded by N

i.e.

hG∈ , where

G is group number x

leaded by node N

. In this case N

sends h

an AREQ message signed by the common

group key between itself and h

after

incrementing

N 's nonce by one ( 1

({,,,,(,1)}).

ip ju j

Sign AREQ N G N G H KS r +

Note that

h is already has an authenticated

copy of its group leader's public key

KU ; so N

have not to authenticate

itself to h

ii. A member of

G which means that

Nh G∈ with

N as their leader: In

this case

N appends its public key signed

K to the AREQ message and send

the whole message to h

signed by the

common group key between itself and h

after incrementing

N 's nonce by one

(

({,,,,(,1)}

|| || ( ))

iNNi

ip ju j

NK N

Sign AREQ N G N G H KS r

KU Sign KU

iii. The leader of group

G i.e.

1 q

hN= : In

this case

N appends its public key signed

K to the AREQ message and send

the whole message to h

signed by the

common group key between itself and h

after incrementing

N 's nonce by one

(

({,,,,(,1)}

|| || ( ))

ihNi

ip ju j

NK N

Sign AREQ N G N G H KS r

KU Sign KU

5. When the first member of the authentication

chain, h

, receives the AREQ message, it

verifies the signature of

i.e. get an

authenticated copy of the public key of N

. We

have three cases:

SECRYPT 2009 - International Conference on Security and Cryptography

278

i. If

hG∈ , then h

is already has an

authenticated copy of

; because N

is h

's leader and each node should have an

authenticated copy of its group leader's

public key as discussed above.

ii. If

Nh G∈ , then h

sends

N 's

public key signed by

K along with its

public key

KU to

N . When

N receives

KU KU and

()

NN i

Sign KU from h

, it generates

K using the KDF,

(,)

qi q i

NN N N

K KDF KM KU=

then

verifies the signature

()

NN i

Sign KU . Node

N generates

(,)

Nh q h

KKDFKMKU= and signs

KU with

()

Nh i

Sign KU ,

then sends both

KU and

()

Nh i

Sign KU to h

. When h

receives

()

Nh i

Sign KU , it verifies

the signature using

K and get the

authenticated copy of

N 's public key.

iii. If

1 q

hN= , then h

generates

using the KDF,

(, )

hN h N

KKDFKMKU= then

verifies the signature

()

hN i

Sign KU

received before from

N and get the

authenticated copy of

N 's public key.

6. After h

verifies the signature, it append the

authenticated

KU to the AREQ message,

{, , , ,( , 1)}||

ip ju j N

REQ N G N G H KS r KU+

,and sign the whole message by the common

group key between itself and the next member

in the authentication chain, h

pointed to by

"Next Leader" field in its authentication chain

table; because both h

and h

belong to the same

group which mean that they trust each other. As

we mentioned before, every two successive

nodes in the authentication chain trust each

other because they are belong to same group.

7. Upon receiving the signed AREQ message from

the last member of the authentication chain

h ,

verifies the signature using the group key it

shares between itself and the

h then compare

the two copies of

KU (the one from MREQ

and the one that it received from

h ). The

destination node generates KS, increment

r by

one, compute the hash value

(, 1)

HKSr

and compare it to that it received form

h in the

AREQ message. This means that the destination

node got a confirmation from the source node

that it received the destination node's public

key,

KU , by the MREP message. Node N

then, sends an Authentication Reply (AREP)

message to the last member of the

authentication chain

h pointed to by "Next

Leader" field in its authentication chain table,

this message is signed by the common group

key between itself and

h . The last member of

the authentication chain should be one of the

following:

i. A member of a group leaded by N

i.e.

hG∈ , where

G is group number y

leaded by node N

.: In this case N

sends

an AREP message signed by the common

group key between itself and

h after

incrementing

N 's nonce by one ( 1

)

to prevent replay attack,

({,,,,(,1)})

ip ju i

Sign AREP N G N G H KS r +

ii. A member of

G which means that

jn u

Nh G∈ with

N as their leader: In

this case

N appends its public key signed

K to the AREP message and send

the whole message to

h signed by the

common group key between itself and

after incrementing

N 's nonce by one

AD-HOC ON DEMAND AUTHENTICATION CHAIN PROTOCOL - An Authentication Protocol for Ad-hoc Networks

279

(

r + ).

({,,,,(,1)}

|| || ( ))

jNNj

ip ju i

NK N

Sign AREP N G N G H KS r

KU Sign KU

iii. The leader of group

i.e.

: In

this case

N appends its public key signed

K to the AREP message and send

the whole message to

h signed by the

common group key between itself and

after incrementing

N 's nonce by one

(

r + ).

({,,,,(,1)}

|| || ( ))

jhNj

ip ju i

NK N

Sign AREP N G N G H KS r

KU Sign KU

8. When the last member of the authentication

chain,

h , receives the AREP message, it

verifies the signature of

KU i.e. get an

authenticated copy of the public key of N

. We

have three:

i. If

hG∈ , then

h is already has an

authenticated copy of

KU ; because N

h 's leader and each node should have

an authenticated copy of its group leader's

public key as we discussed above.

ii. If

jn u

Nh G∈

, then

h sends

N 's

public key signed by

K along with its

public key

KU to

N . When

N receives ,

KU KU and

()

NN j

Sign KU from

h , it generates

K using the KDF,

(,)

vj v j

NN N N

KKDFKMKU= then

verifies the signature

()

NN j

Sign KU . Node

generates

(, )

vn n

Nh v h

K KDF KM KU= and

signs

KU with

K ,

()

Nh j

Sign KU , then sends both

and

()

Nh j

Sign KU to

h .

When

h receives

()

Nh j

Sign KU , it

verifies the signature using

K and get

the authenticated copy of

's public key.

iii. If

, then

h generates

using the KDF,

(, )

nj n j

hN h N

K KDF KM KU

then

verifies the signature

()

hN j

Sign KU

received before from

N and get the

authenticated copy of

N 's public key.

9. After h

verifies the signature, it append the

authenticated

KU to the signed AREP

message

{, , , ,( , 1)}||

ip ju i N

AREP N G N G H KS r KU+

and sign the whole message by the common

group key between itself and the previous

member in the authentication chain,

−

pointed to by "Next Leader" field in its

authentication chain table; because both h

and

−

belong to the same group which mean that

they trust each other. As we mentioned before,

every two successive nodes in the authentication

chain trust each other because they are belong to

one group.

10. Upon receiving the signed AREP message from

the first member of the authentication chain

h ,

verifies the signature using the group key it

shares between itself and the

h then compare

the two copies of

KU (the one from MREP

and the one that it received from

h ). The

source node generate KS, increment

r by one,

compute the hash value

(, 1)

HKSr+ and

compare it to that it received form

h in the

AREP message. If they are the same, the source

node is sure that the destination node gets the

right session key. AREP message format is

similar to AREQ message format.

SECRYPT 2009 - International Conference on Security and Cryptography

280

4 DISSCUSION AND ANALYSIS

In this section we provide a detailed analysis

evaluating the security and performance of our

proposed authentication protocol. The metrics for

the performance evaluation are the communication

overhead and computation costs (Du et al., 2005).

The security analysis of our proposed scheme is

based on formal verification techniques. We present

a detailed verification of our proposed key AOAC

authentication protocol using the logic of Gong,

Needham and Yahalom (Gong et al., 1990).

4.1 Security Analysis

In our AOAC protocol, node-to-node authentication

depends on TAP protocol. So, in this section we

discuss the security analysis of TAP protocol

discussed in section 3.2 by applying formal analysis

and the GNY logic. Without lose of generality we

suppose that the authentication chain consists of

three nodes (

123

,,hh h) and the sender node is A

and the receiver node is B where

hG∈ , in

this case

hG∈ ,

G∈ ; since

each node must belongs to only one group leaded by

only one leader. This case is the most general case.

The protocol works as follows:

M1.

ABrKU→

M2.

ArKU→

M3.

114

:({,,,,(,1)}

|| || ( ))

AK A

AhSignAREQAGBGHKSr

KU Sign KU

→+

M4.

:, ()

hK A

h L KU Sign KU→

M5.

:(,)

LhSign TKU→

M6.

12 1 4

:({,,,,(,1)}

|| || )

hhSignAREQAGBGHKSr

TKU

→+

M7.

23 1 4

:({,,,,(,1)}

|| || )

hhSignAREQAGBGHKSr

TKU

→+

M8.

314

:({,,,,(,1)}

|| || )

hBSignAREQAGBGHKSr

TKU

→+

The goal is to prove that B got an authenticated

copy of A's public key and that it computed the peer-

to-peer shared key between itself and A. As we see

we only have to prove that B got an authenticated

copy of A's public key; because the second goal

follows from the first goal since both A and B use

ECDH protocol in computing the common shared

key between themselves. Also we can consider the

group key of two nodes belonging to the same group

as a shared key between those two nodes e.g. we can

consider

K as

,Ah

K because

Ah G∈ . Node

B follows the same steps to deliver the AREP

message to node B as we discussed above, so we

only prove the first part of the protocol i.e. B got an

authenticated copy of A's public key. From the above

discussions, the above steps will take the following

form:

M1.



M2.

Ar K



M3.

{, , ( ), ,{, } }

AAAh

KAAbBKK

hABE K KrK

−

++

M4.

,,{}

hA AK

LKK K

++

M5.

{, } ~

hTK A

+>⎯⎯⎯→

M6.

{, ,, ,{, } } ~

Ahh

Ab BKK

hABTKrK A

−

+>⎯⎯⎯→

M7.

{, ,, ,{, } } ~

Ahh

Ab BKK

hABTKrK A

−

+>⎯⎯⎯→

M8.

{, ,, ,{, } } ~

AhB

Ab BKK

BABTKrK A

−

++ >⎯⎯⎯→

Where

Ah G

KK≡ ,

12 2

hh G

KK≡ ,

23 3

hh G

KK≡

hB G

KK≡

and

,Lh

K and

,LA

are the one-to-one shared keys between (L, h

)

and (L, A) respectively. Notice that we replace

H(KS, r

) by {, }

bBK

−

. When node B receive

H(KS, r

) in step M8, the following statements are

true:

• Node B is sure that node A received KU

in step

• Node B is also sure that KU

, received in step

M1, is sent by node A.

• Node B is sure that H(KS, r

) is fresh because it

is a function of r

• H(KS, r

) can only computed by either A or B

and can be verified by B.

The above four statement are true because KS,

which is an ECDH shared key between A and B, can

be calculated only by either A as a function of KR

(which is only known by A) and KU

or by B as a

function of KR

(which is only known by B)

and

. As we know that GNY logic does not have

notation for key agreement operations i.e. we cannot

express KS in GNY logic. So to work around this

problem we try to find notations in GNY logic that

AD-HOC ON DEMAND AUTHENTICATION CHAIN PROTOCOL - An Authentication Protocol for Ad-hoc Networks

281

achieve the above four statements this notation

{, }

bBK

−

+ . It is clear that the first two

statement are true because the encryption is done

using A's private key which is only known by A.

Also B sure that

{, }

bBK

−

+ is fresh because it is

a function of r

. Finally A is the only node that can

generate

{, }

bBK

−

+ and B can verify it. So it is

safe to replace H(KS, r

) by {, }

bBK

−

+ in the

above symbolic steps just to prove the security of

our protocol. Note that we cannot replace H(KS, r

)

{, }

bBK

−

+ in the original protocol because

we want to prove that B is sure that A computed the

peer-to-peer shared key between itself and B. In the

GNY version this goal follows from the first goal

discussed above which is to prove that B got an

authenticated copy of A's public key. Notice also

that we replace signature (Sign) with encryption (E)

which does not affect the analysis. We did this

because there is no notation for signature operation

in the GNY logic. We expressed the assumptions

(initial possessions and beliefs) and goals (target

possessions and beliefs) as statements in a symbolic

notation. To prove the target possessions and beliefs,

we use the SPEER II (Saul and Hutchison, 2001).

SPEAR II, the Security Protocol Engineering and

Analysis Resource II, is a protocol engineering tool.

The SPEAR II tool consists of four components that

integrated into one consistent and unified graphical

interface: a protocol specification environment

(GYPSIE), a GNY statement construction interface

(Visual GNY), a Prolog-based GNY analysis engine

(GYNGER) and a message rounds calculator.

GYNGER is a Prolog-based analyzer that performs

automated analysis of protocols by using the GNY

modal logic. Using this tool and the initial

possessions and beliefs as input to SPEAR II, the

target possessions and beliefs are proved.

4.2 Performance Analysis

In this section we provide a detailed analysis

evaluating the performance of our proposed

authentication protocol. Computation and

communication costs are function of the network

size. So to compute those costs we first have to

compute the average number of nodes that each

node deals with. Many protocols assume that each

node in the network deals with all the nodes in the

network, so the computation and communication

costs depend on the exact network size. In our

AOAC protocol, node-to-node authentication

depends on TAP protocol. So, computation and

communication costs in our scheme depend on the

length of the authentication chain (AC). Since the

AC consists of leader nodes, then the length of AC

equal to at most the number of leader nodes in the

network. So, we first have to find the average

number of leader nodes in the network. We use

simulation to compute this value.

Figure 5: Relationship between N and the average number

of leader nodes.

Figure 6: Relationship between N and the ratio of the

number of leader nodes to N.

4.2.1 Simulation

We designed a simulator that simulates our proposed

protocol. We use C++ to create our simulator. The

simulator is used to compute the average number of

leader nodes in the network. In our simulation we

use the random waypoint mobility model. Each node

moves at a speed uniformly distributed between 0.5

and 20 m/s towards a location randomly selected in a

square environment space of 1000m × 1000m. When

it reaches the destination, it waits for a pause time of

maximum 60 sec. and then moves towards a new

location. The number of nodes N grows from 100 to

1000 nodes and increase by 100 nodes each time

Each simulation runs for 1000 seconds of simulated

time and we get the result of the simulation every

100 seconds. The transmission range is 300.

SECRYPT 2009 - International Conference on Security and Cryptography

282

In Figure 5, which is based on our simulation

results, we plot the total number of nodes N against

the average number of leader nodes. As we see from

the figure that the average number of leader nodes

increases as the total number of nodes increases. To

find the order of the average number of leader nodes

with respect to N and to show its growth rate, we

find the curve that fit the average number of leader

nodes.

The curve fitting analyses were performed on

LAB Fit (Silva and Silva, 1999-2007), see Figure 5.

Using LAB Fit, we found that the following

equation (1) yields the best approximation or best fit

for the measured number of leader nodes for given

N. We use the Coefficient Correlation (

) to find

the goodness of fit and found

= 0.991848 which

is a high value and which indicates that the average

number of leader nodes increases as the total number

of nodes increases.

0.6 .ln( )yxx=

(1)

(0.6 / ) / ln( )yxx=

(2)

Where x is the total number of nodes and y

the average number of leader nodes. We might ask

about the rate of growth of y

in equation (1). As we

see from Figure 6 the ratio of the average number of

leader nodes to the total number of nodes decrease

as the total number of nodes increase which means

that the size of the authentication chain, which

consists of leader nodes, will not approach the total

number of nodes. Also, if we apply the curve fitting

analyses discussed above we get equation (2) with a

correlation coefficient

= -0.937958.

From the above discussion we see that the

average number of leader nodes has a value of

(ln())ON N, which considered a reasonable

value with respect to the total number of nodes N,

with decreasing growth rate which insure that it will

never approaches N.

4.2.2 Complexity Analysis

As we discussed in section 3, AOAC protocol is

based on the TAP protocol, so here we compute the

computation complexity of TAP protocol. We

compute the commutation complexity with respect

to the sender node, the receiver node, and to any

node in the authentication chain. As discussed in

section 3.2, a sender performs two symmetric

encryptions and one hash operation before sending

its AREQ message to the first node in the

authentication chain and performs one symmetric

decryption operation after he gets the AREP message

from the first node in the authentication chain. Also

the receiver node performs one symmetric

decryption operation after he gets the AREQ

message from the last node in the authentication

chain and performs two symmetric encryption

operations and one hash operation before sending its

AREP to the last node in the authentication chain.

Each node in the authentication chain performs two

symmetric decryption operations to decrypt the

incoming AREQ and AREP messages received from

the previous and next nodes respectively and two

encryption operations to encrypt the outgoing AREQ

and AREP messages sent to the next and previous

nodes respectively. So, it is clear that the

computation cost of our proposed authentication

protocol is small compared to other authentication

protocol that use asymmetric encryption techniques;

this is because the computation cost of symmetric

encryption is very small compared to that of

asymmetric encryption.

Now we consider the communication cost. TAP

protocol needs two rounds with respect to the sender

and receiver to authenticate each other; because each

of them waits for two messages from the other one

to complete the authentication process. The total

number of messages of TAP protocol depends on the

length of the authentication chain which is at most

equal to the total number of leader nodes; because

the authentication chain consists only of leader

nodes. But form Equation (1) the number of leader

modes is

0.6 .ln( )nn

which means that the

average length of the authentication chain is of order

(.ln())On n. Now we calculate the number of

message for the sender, the receiver and for each

node in the authentication chain. From the

discussion in section 3 we conclude that the number

of message for the sender is four and so is the

receiver. The total number of message for each node

in the authentication chain is two. So, the total

number of messages is

4 4 2*0.6 .ln( ) 8 1.2 .ln( )nn nn++ =+ i.e.

TAP protocol requires

81.2 .ln()nn+ global

unicasts, which is of order

(.ln())On n

.be a

vertical spacing of 12-point between authors.

AD-HOC ON DEMAND AUTHENTICATION CHAIN PROTOCOL - An Authentication Protocol for Ad-hoc Networks

283

5 CONCLUSIONS

AOAC which is an authentication protocol that

provide authentication to the key establishment

protocol we proposed in (Hamad et al., 2008a) and

allows any two nodes to establish a peer-to-peer key

for authentication and one-to-one secure

communication. In our proposed authentication

protocol we use symmetric key cryptography to

provide authentication compared to may other

authentication protocol that use public key

cryptograph. It assumes that the network is

partitioned into a set of groups and each group is

leaded by one leader with leaders connecting these

groups. When we say that leaders connecting

groups, we do not mean a physical connection, we

mean an authentication connection i.e. if node N

connects two group (belongs to one group and leads

another one or leads both groups), then the only way

for these two groups to authenticate each other is

through N

; because N

shares a key with the first

group and shares another key with the other group.

So, when a source node wants to authenticate a

destination node, it has to find a set of group leaders

that authenticate the source node to the destination

node. It is divided into two sub-protocols:

• Authentication Chain Discovery Protocol

• Transitive Authentication Protocol

We prove the security of AOAC protocol using the

GNY logic and use simulation and complexity

analysis to measure its performance. AOAC has low

computation overhead since it use symmetric key

encryption for verifying the identity of nodes, low

communication of order

(/ln())On n and low

memory cost which is constant.

REFERENCES

C. R. Murthy and B. S. Manoj, Ad Hoc Wireless Networks

- Architectures and Protocols: Person Education,

2004.

L. Zhou and Z. J. Haas, "Securing Ad Hoc Networks,"

IEEE Network Magazine, vol. 13, pp. 24-30, 1999.

J. Kong, P. Zerfos, S. L. H. Luo, and L. Zhang, "Providing

robust and ubiquitous security support for mobile ad

hoc networks," presented at IEEE ICNP, 2001.

M. Narasimha, G. Tsudik, and J. H. Yi, "On the Utility of

Distributed Cryptography in P2P and MANETs: the

Case of Membership Control," presented at IEEE

ICNP, 2003.

H. Luo, P. Zerfos, J. Kong, and L. Z. S. Lu, "Self-securing

Ad Hoc Wireless Networks," presented at ISCC, 2002.

A. M. Hamad, T. I. El-Areef, M. A. Shouman, and W. I.

Khedr, "Local Broadcast and Transitive

Authentication Based Key Establishment Scheme for

Wireless Ad-hoc Network," the Egyptian Informatics

Journal,, June 2008a.

A. M. Hamad, T. I. El-Areef, M. A. Shouman, and W. I.

Khedr, "Key Establishment Protocols for Wireless

Sensor Networks," the International Journal of

Intelligent Computing and Information Sciences

,January 2008b.

P. R. J. Östergård, "A fast algorithm for the maximum

clique problem," Discrete Applied Mathematics vol.

120, pp. 197-207, 2002.

W. Du, R. Wang, and P. Ning, "An efficient scheme for

authenticating public keys in sensor networks,"

presented at Proceedings of the 6th ACM international

symposium on Mobile ad hoc networking and

computing Urbana-Champaign, IL, USA 2005.

L. Gong, R. Needham, and R. Yahalom, "Reasoning about

Belief in Cryptographic Protocols," presented at IEEE

Symposium on Security and Privacy, Oakland, CA,

USA, 1990.

E. Saul and A. C. M. Hutchison, "Using GYPSIE,

GYNGER and Visual GNY to Analyze Cryptographic

Protocols in SPEAR II," presented at Eighth Annual

Working Conference on Information Security

Management and Small Systems Security, Las Vegas,

Nevada, September 2001.

Silva, W. P., and C. M. D. P. S. Silva, "LAB Fit Curve

Fitting Software (Nonlinear Regression and Treatment

of Data Program) V 7.2.39 (1999-2007), online,

available from world wide web:

http://www.angelfire.com/rnb/labfit/."

SECRYPT 2009 - International Conference on Security and Cryptography

284