SEQUENTIAL SYMBOL SYNCHRONIZERS BASED ON PULSE

COMPARATION

Antonio D. Reis

1,2

, Jose F. Rocha

, Atilio S. Gameiro

and Jose P. Carvalho

Dep. de Electrónica e Telecomunicações / Instituto de Telecomunicações, Universidade de Aveiro, 3810 Aveiro, Portugal

Dep. de Fisica / U. D. Remota, Universidade da Beira Interior Covilhã, 6200 Covilhã, Portugal

Keywords: Synchronism, Telecommunications, Digital Communications.

Abstract: This work presents a sequential symbol synchronizer, that is based on a pulse comparation, between a phase

variable pulse and a reference fixed pulse. This synchronizer has two types namely the both data transitions

and the positive data transitions. Each type has two versions which are the manual and the automatic. The

objective is to study the synchronizers and evaluate the output jitter UIRMS (Unit Interval Root Mean

Square) versus the input SNR (Signal Noise Ratio).

1 INTRODUCTION

This work studies a sequential symbol synchronizer,

based on pulse comparation, between a phase

variable pulse and a reference fixed pulse.

The input data transitions and the clock positive

transitions produces between them, a variable pulse

Pv. The input data transitions with the help of a T/2

delay or clock provides a fixed pulse Pf (Imbeaux,

1983), (Rosenkranz, 1982), (Witte, 1983), (Hogge,

1985), (Simon and Lindsey, 1977).

If the clock is delayed, Pv is greater than Pf, and

then is applied a positive pulse Pe (Pv-Pf) that

advances it. On the other hand, if the clock is

advanced, Pv is lesser than Pf, and then is applied a

negative pulse Pe (Pv-Pf) that delays it (Carruthers,

Falconer, Sandler and Strawczynski, 1990), (Huber

and Liu, 1992), (D’Amico, D’Andrea and Regianni,

2001), (Dobkin, Ginosar and Sotiriou, 2004),

(Noels, Steendam and Moeneclaey, 2006).

The clock positive transition samples the data

symbols at the maximum opening eye diagram.

Fig.1 shows the functioning principle of the

referred synchronizer.

Kf is the phase comparator gain, F(s) is the loop

filter, Ko is the VCO (Voltage Controlled

Oscillator) gain and Ka is the loop amplification that

controls the root locus and then the loop desired

characteristics.

Following, we present the both transitions

synchronizer with its versions manual and

automatic.

Figure 1: Aspect of synchronizers based on pulse

comparation.

Next, we present the positive transitions

synchronizer with its versions manual and

automatic.

After, we present the design and tests.

Then, we present the results.

Finally, we present the conclusions.

2 BOTH TRANSITIONS

SYNCHRONIZERS

The both transitions synchronizer takes synchronism

information of the both data transitions (positive and

negative). This synchronizer has the following

versions manual and automatic.

The variable pulse Pv is similar in the two

versions, but the difference is in the fixed pulse Pf)

(Reis, Rocha, Gameiro and Pacheco, 2008).

105

D. Reis A., F. Rocha J., S. Gameiro A. and P. Carvalho J. (2009).

SEQUENTIAL SYMBOL SYNCHRONIZERS BASED ON PULSE COMPARATION.

In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 105-109

DOI: 10.5220/0002236701050109

 SciTePress

2.1 Both Transitions and Manual

Version

The manual version uses a fixed pulse, based on an

exor with delay Δt=T/2, previously adjusted by the

manufacturer, that produces the fixed pulse Pf

(Fig.2).

Figure 2: Synchronizer both transitions and manual (b-m).

The delay Δt=T/2 with exor produces a fixed

pulse Pf that determines the rhythm of charge.

Fig.3 shows the waveforms of the synchronizer

both transitions and manual.

Figure 3: Waveforms of the synchronizer both transitions

manual.

The error pulse Pe diminishes and disappear at

the equilibrium point.

2.2 Both Transitions and Automatic

Version

The automatic version uses a fixed pulse, based on

an exor with flip flop 1, automatically adjusted, that

produces the fixed pulse Pf (Fig.4).

Figure 4: Synchronizer both transitions and automatic (b-

a).

The flip flop1 with exor produces a fixed pulse

Pf that determines the rhythm of charge.

Fig.5 shows the waveforms of the synchronizer

both transitions and automatic.

Figure 5: Waveforms of the synchronizer both transitions

automatic.

The error pulse Pe don’t disappear, but the

positive area is equal to the negative at the

equilibrium point.

3 POSITIVE TRANSITIONS

SYNCHRONIZERS

The positive transitions synchronizer takes

synchronism information only of the positive data

transitions. Can be useful in nonlinear systems

where the period multiplicity is guaranteed only

between positive transitions. This synchronizer has

the following versions manual and automatic. The

variable pulse Pv is similar in the two versions, but

the difference is in the fixed pulse Pf (Reis, Rocha,

Gameiro and Pacheco, 2008).

3.1 Positive Transitions and Manual

Version

The manual version uses a fixed pulse, based on an

AND with delay Δt=T/2, previously adjusted by the

manufacturer, that produces the fixed pulse Pf

(Fig.6).

Figure 6: Synchronizer positive transitions and manual (p-

m).

The delay Δt=T/2 with AND produces a fixed

WINSYS 2009 - International Conference on Wireless Information Networks and Systems

106

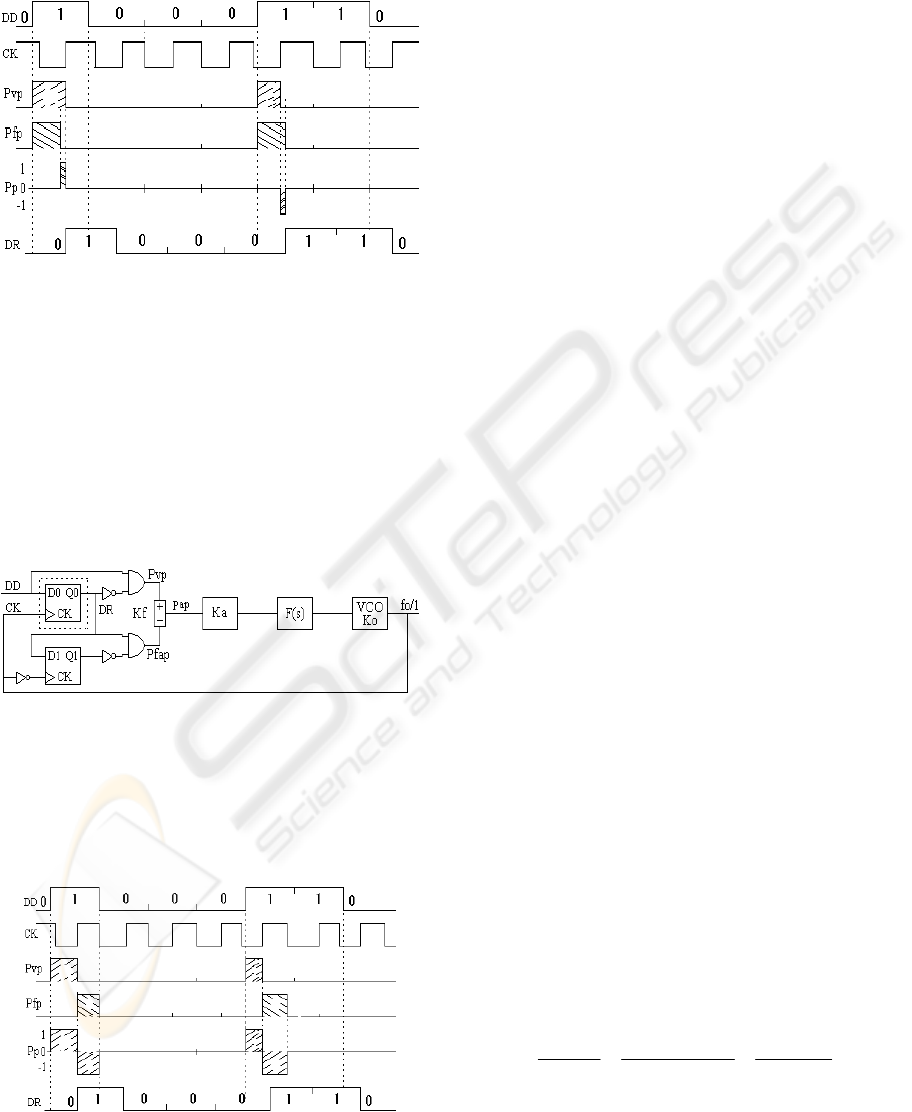
pulse Pf that determines the rhythm of charge.

Fig.7 shows the waveforms of the synchronizer

positive transitions and manual.

Figure 7: Waveforms of the synchronizer positive

transitions manual.

The error pulse Pe diminishes and disappear at

the equilibrium point

3.2 Positive Transitions and Automatic

Version

The automatic version uses a fixed pulse, based on

an AND with flip flop 1, automatically adjusted, that

produces the fixed pulse Pf (Fig.8).

Figure 8: Synchronizer positive transitions and automatic

(p-a).

The flip flop1 with AND produces a fixed pulse

Pf that determines the rhythm of charge.

Fig.9 shows the waveforms of the synchronizer

positive transitions and automatic.

Figure 9: Waveforms of the synchronizer positive

transitions automatic.

The error pulse Pe don’t disappear but the

positive area is equal to the negative at the

equilibrium point.

4 DESIGN, TESTS AND RESULTS

We will present the design, tests and results of the

referred synchronizers (Reis, Rocha, Gameiro and

Pacheco, 2001).

4.1 Design

To get guaranteed results, it is necessary to

dimension all the synchronizers with equal

conditions. Then it is necessary to design all the

loops with identical linearized transfer functions.

The general loop gain is Kl=Kd.Ko=Ka.Kf.Ko

where Kf is the phase comparator gain, Ko is the

VCO gain and Ka is the control amplification factor

that permits the desired characteristics.

For analysis facilities, we use a normalized

transmission rate tx=1baud, what implies also

normalized values for the others dependent

parameters. So, the normalized clock frequency is

fCK=1Hz.

We choose a normalized external noise

bandwidth Bn = 5Hz and a normalized loop noise

bandwidth Bl = 0.02Hz. Later, we can disnormalize

these values to the appropriated transmission rate tx.

Now, we will apply a signal with noise ratio

SNR given by the signal amplitude Aef, noise

spectral density No and external noise bandwidth

Bn, so the SNR = A

/(No.Bn). But, No can be

related with the noise variance σn and inverse

sampling Δτ=1/Samp, then No=2σn

.Δτ, so

SNR=A

/(2σn

.Δτ.Bn) = 0.5

/(2σn

*10

-3

*5)=

25/σn

After, we observe the output jitter UI as function

of the input signal with noise SNR. The dimension

of the loops is

- 1

order loop:

The loop filter F(s)=1 with cutoff frequency

0.5Hz (Bp=0.5 Hz is 25 times bigger than

Bl=0.02Hz) eliminates only the high frequency, but

maintain the loop characteristics.

The transfer function is

H(s)=

G(s)

1G(s)+

KdKoF s

sKdKoFs

KdKo

sKdKo

()

(1)

the loop noise bandwidth is

SEQUENTIAL SYMBOL SYNCHRONIZERS BASED ON PULSE COMPARATION

107

Bl =

KdKo

fKo

= 0.02Hz (2)

Then, for the analog synchronizers, the loop

bandwidth is

Bl=0.02=

(Ka.Kf.Ko)/4 with (Km=1, A=1/2, B=1/2;

Ko=2π)

(Ka.Km.A.B.Ko)/4 = 0.02 -> Ka=0.08*2/

(3)

For the hybrid synchronizers, the loop bandwidth is:

Bl=0.02=

(Ka.Kf.Ko)/4 with (Km=1, A=1/2, B=0.45;

Ko=2π)

(Ka.Km.A.B.Ko)/4 = 0.02 -> Ka=0.08*2.2/

(4)

For the combinational synchronizers, the loop

bandwidth is:

Bl=0.02=

(Ka.Kf.Ko)/4 with (Kf=1/π; Ko=2π)

(Ka*1/

)/4 = 0.02 -> Ka=0.04 (5)

For the sequential synchronizers, the loop

bandwidth is:

Bl=0.02=

(Ka.Kf.Ko)/4 with (Kf=1/2π; Ko=2π)

(Ka*1/2

)/4 =0.02 -> Ka=0.08 (6)

The jitter depends on the RMS signal Aef, on the

power spectral density No and on the loop noise

bandwidth Bl.

For analog PLL the jitter is:

σφ

=Bl.No/Aef

=Bl.2.σn

.Δτ=0.02*10

*2σn

/0.5

=16*10

-5

.σn

For the others PLLs the jitter formula is more

complicated.

- 2

order loop:

The second order loop is not shown here, but the

results are identical to the ones obtained above for

the first order loop.

4.2 Tests

The following figure (Fig.10) shows the setup that

was used to test the various synchronizers.

Figure 10: Block diagram of the test setup.

The receiver recovered clock with jitter is

compared with the emitter original clock without

jitter, the difference is the jitter of the received

clock.

4.3 Jitter Measurer (Meter)

The jitter measurer (Meter) consists of a RS flip

flop, which detects the random variable phase of the

recovered clock (CKR), relatively to the fixed phase

of the emitter clock (CKE). This relative random

phase variation is the recovered clock jitter (Fig.11).

Figure 11: The jitter measurer (Meter).

The other blocks convert this random phase

variation into a random amplitude variation, which

is the jitter histogram.

Then, the jitter histogram is sampled and

processed by an appropriate program, providing the

RMS jitter and the peak to peak jitter.

4.4 Results

We will present the results (output jitter UIRMS

versus input SNR) for the four synchronizers.

Fig.12 shows the jitter-SNR curves of the four

synchronizers: both transitions and manual (b-m),

both transitions and automatic (b-a), positive

transitions and manual (p-m), positive transitions

and automatic (p-a).

Figure 12: Jitter-SNR curves of the four synchronizers(b-

m,b-a,p-m,p-a).

We verify, that generally the output jitter

UIRMS diminishes exponentially with the input

SNR increasing.

For high SNR, the four curves tend to be similar

although with a slight disadvantage of the positive

transitions automatic (p-a). However, for low SNR

the both transitions manual (b-m) is the best,

followed of the positive transitions manual (p-m).

The both transitions automatic (b-a) and the positive

transitions automatic (p-a) are the worst and similar.

WINSYS 2009 - International Conference on Wireless Information Networks and Systems

108

5 CONCLUSIONS

We studied four synchronizers, namely the both

transitions manual (b-m), the both transitions

automatic (b-a), the positive transitions manual (p-

m) and the positive transitions automatic (p-a).

Then, we tested their output jitter UIRMS versus

input SNR.

We observed that, generally, the jitter diminishes

almost exponentially with the SNR increasing.

We verified, that for high SNR, the jitter of the

four synchronizers are similar, although with a little

disadvantage of the positive transitions automatic

(p-a), this is comprehensible since it has two flip

flops and stays more time in the error state until the

next correction transition.

However, for low SNR, the both transitions

manual (b-m) is the best since only one flip flop

contributes to the error state and the time in the error

state is lesser. After is the positive transitions

manual (p-m) since only one flip flop contributes to

the jitter but the time in the error state is greater (two

times). In last, are the two automatic versions (b-a

and p-a) since they have two flip flops that

contributes to the jitter and are similar. Anyway, the

last case is still aggravated by the greater time in the

error state.

ACKNOWLEDGEMENTS

The authors are grateful to the program FCT

(Foundation for sCience and Technology) /

POCI2010.

REFERENCES

Imbeaux, J. C., 1983. Performance of the delay-line

multiplier circuit for clock and carrier

synchronization. IEEE Journal on Selected Areas in

Communications p.82 Jan.

Rosenkranz, W., 1982. Phase Locked Loops with limiter

phase detectors in the presence of noise. IEEE Trans.

on Communications com-30 Nº10 pp.2297-2304. Oct.

Witte, H. H., 1983. A Simple Clock Extraction Circuit

Using a Self Sustaining Monostable Multivibrator

Output Signal. Electronics Letters, Vol.19, Is.21,

pp.897-898, Oct.

Hogge, C. R., 1985. A Self Correcting Clock Recovery

Circuit. IEEE Tran. Electron Devices p.2704 Dec.

Reis, A. D., Rocha, J. F., Gameiro, A. S., Carvalho, J. P.,

2001. A New Technique to Measure the Jitter. Proc.

III Conf. on Telecommunications pp.64-67 FFoz-PT

23-24 Apr.

Simon, M. K., Lindsey, W. C., 1977. Tracking

Performance of Symbol Synchronizers for Manchester

Coded Data. IEEE Transactions on Communications

Vol. com-2.5 Nº4, pp.393-408, April.

Carruthers, J., Falconer, D., Sandler, H., Strawczynski, L.,

1990. Bit Synchronization in the Presence of Co-

Channel Interference. Proc. Conf. on Electrical and

Computer Engineering pp.4.1.1-4.1.7, Ottawa-CA 3-6

Sep.

Huber, J., Liu, W., 1992. Data-Aided Synchronization of

Coherent CPM-Receivers. IEEE Transactions on

Communications Vol.40 Nº1, pp.178-189, Jan.

D’Amico, A., D’Andrea, A., Reggianni, 2001. Efficient

Non-Data-Aided Carrier and Clock Recovery for

Satellite DVB at Very Low SNR. IEEE Jou. on

Sattelite Areas in Comm. Vol.19 Nº12 pp.2320-2330,

Dec.

Dobkin, R., Ginosar, R., Sotiriou, C. P., 2004. Data

Synchronization Issues in GALS SoCs. Proc. 10th

International Symposium on Asynchronous Circuits

and Systems, pp.CD-Ed., Crete-Greece 19-23 Apr.

Noels, N., Steendam, H., Moeneclaey, M., 2006.

Effectiveness Study of Code-Aided and Non-Code-

Aided ML-Based Feedback Phase Synchronizers.

Proc. IEEE Int Conf. on Comm.(ICC’06) pp.2946-

2951, Ist.-TK, 11-15 Jun.

Reis, A. D., Rocha, J. F., Gameiro, A. S., Carvalho, J. P.,

2008. The Electromagnetic Wave and the Principle of

the Telecommunications. Proc. VI Sym. on Enabling

Optical Network and Sen. (SEONs 2008) p.87-88, Av-

PT 29-29 Jun.

SEQUENTIAL SYMBOL SYNCHRONIZERS BASED ON PULSE COMPARATION

109