A NEW HYBRID GENETIC ALGORITHM FOR

MAXIMUM INDEPENDENT SET PROBLEM

Saeed Mehrabi

, Abbas Mehrabi

and Ali D. Mehrabi

Department of Computer Science, Shahid Bahonar University of Kerman, Kerman, Iran

Department of Computer Engineering, Islamic Azad University, South Tehran Branch, Tehran, Iran

Department of Mathematical and Computer Science, Yazd University, Yazd, Iran

Keyword: Algorithmic Graph Theory, Combinatorial Optimization, Maximum Independent Set Problem, Genetic

Algorithms.

Abstract: In recent years, Genetic Algorithms (GAs) have been frequently used for many search and optimization

problems. In this paper, we use genetic algorithms for solving the NP-complete maximum independent set

problem (MISP). We have developed a new heuristic independent crossover (HIX) especially for MISP,

introducing a new hybrid genetic algorithm (MIS-HGA). We use a repair operator to ensure that our

offsprings are valid after mutation. We compare our algorithm, MIS-GA, with an efficient existing

algorithm called GENEsYs. Also, a variety of benchmarks are used to test our algorithm. As the

experimental results show: 1) our algorithm outperforms GENEsYs, and, 2) applying HIX to genetic

algorithms with an appropriate mutation rate, gives far better performance than the classical crossover

operators.

1 INTRODUCTION

Genetic Algorithms (GAs), (Goldberg, 1989), are

search algorithms based on the mechanism of natural

selection and natural genetics. Recently, GAs have

frequently been used for solving many search and

optimization problems (see e. g. Hifi (1997),

Mehrabi and Mehrabi (2009a) or Mehrabi and

Mehrabi (2009b)). The basic concept of GA is

designed to simulate the processes in natural system

necessary for evolution, specifically for those that

follow the principle of survival of the fittest, first

laid down by Charles Darwin. The basic steps of a

GA, Bodenhofer (2003), are shown in Figure 1.

A Hybrid Genetic Algorithm (HGA) combines

some heuristic optimization techniques with a

classical GA. The most common form of HGA uses

this optimization phase to improve the strings

produced by genetic recombination. The resulting

improvements are then coded onto the strings

processed by the GA, Whitley (1995). Here, we use

these heuristics to 1) make feasible the single

offspring generated by crossover operator, and, 2)

ensure that the child solution produced after

mutation is valid regarding to MISP constraints.

1.1 The Maximum Independent Set

Problem

The maximum independent set problem can be

stated as follows:

Figure 1: The basic steps of a GA.

Definition 1. The maximum independent set

problem consists of finding the largest subset of

vertices of a graph such that none of these vertices

are connected by an edge. (i.e., all vertices are

independent of each other).

Also, a set V of vertices is said to be feasible if for

Genetic Algorithms Outline

Compute initial population P

;

WHILE stopping condition not fulfilled DO

BEGIN

select individuals for reproduction;

create offsprings by crossing individuals;

eventually mutate some individuals;

compute new generation;

END.

314

Mehrabi S., Mehrabi A. and D. Mehrabi A. (2009).

A NEW HYBRID GENETIC ALGORITHM FOR MAXIMUM INDEPENDENT SET PROBLEM.

In Proceedings of the 4th International Conference on Software and Data Technologies, pages 314-317

DOI: 10.5220/0002253403140317

 SciTePress

each i,j ∈ V : (i , j) ∉ E, where E is the edge set of

graph. The way in which the problem is encoded to

use genetic algorithm, is given in the next section.

In solving the maximum independent set

problem, we also have a solution for another graph

problem: The minimum vertex cover problem (exact

definition of this problem can be found in West

(2001), for example). The close relationship between

these problems is shown by the following Lemma

(see e.g. Papadimitriou and Steiglitz (1982)):

Lemma 2. For any graph G = (V , E) and V' ⊆ V,

the following statements are equivalent:

● V' is the maximum independent set in G.

● V – V' is the minimum vertex cover of G.

Consequently, one can obtain a solution of the

minimum vertex cover problem by taking the

complement of the solution to the maximum

independent set problem, (Hifi, 1997).

2 OUR HYBRID GENETIC

ALGORITHM

In this section, we will present our algorithm. We

just modified the basic GA described in previous

section in such a way that some heuristics is

considered. Our modified GA for MISP is as

follows:

2.1 Representation and Fitness

Function

The first step in designing a genetic algorithm for a

particular problem is to develop a suitable

representation scheme, that's, a way to represent

individuals in the GA population. The standard GA

0-1 binary representation (see e.g. Chu and Beasley

(2004) or Lio, Sakamato and Shimamoto (1997)), is

an obvious choice for MISP. Hence, we use an n-bit

binary string (called chromosome), where n is the

number of vertices in the underlying graph for

MISP. In this representation, a value 0 or 1 at the j

bit (called gene in GA literature) implies that j

vertex of graph is excluded or included in this

solution, respectively.

For unweighted MISP, there is a simple fitness

function that is used. As usual, (see e.g. Chu and

Beasley (2004) or Khuri and Bäck (1994)), we

define the fitness value of an individual, say S, in

GA population as the number of vertices in the

solution, that's:

∑

jSSf

][)( (1)

2.2 Parent Selection

Parent selection is the task of giving reproductive

opportunities to some or all individuals in the

population. Typically, in a GA we need to generate

two parents (according to some policies) who have

one or more children. There are many parent

selection methods in the GA literature, such as

roulette wheel (Goldberg, 1989), tournament

selection method (Chu and Beasley, 2004), steady

state selection and so on. Here, we used a steady

state like selection method, since in successive

generations only 50 % of the current population

changes.

2.3 Heuristic Independent Crossover

and Mutation Operators

Our heuristic crossover operator (HIX), which plays

an important role in our algorithm, can be divided in

two phases, as follows: suppose that two parents P

and P

are selected for crossover. At first phase, we

group up all vertices in either P

or P

into a

temporary set, say M, and sort them in increasing

order by their degrees in underlying graph. At

second phase, we generate our offspring by a simple

greedy approach as follows: successively selecting

lowest degree vertices first from M and setting

corresponding position to 1 in offspring until the

selected vertex can not add to the child solution. In

fact, selecting lower degree vertices first gives more

chance to other vertices to be included into the

solution, so improving the offspring reproductivity

in future generations. As we will see, this simple

greedy algorithm speeds up the convergence rate of

solutions to optimum solution. Figure 2 outlines the

Algorithm HIX.

2.4 Repair Operator

Clearly, the child solution produced by the mutation

operator may not be feasible, because the selected

vertices after mutation may not constitute an

independent set in graph. In order to guarantee

feasibility, a heuristic, called repair operator, based

on a simple greedy algorithm is applied. Since its

greedy approach activity is mostly like one that used

in crossover operator, along some subtle differences,

we don't mention it in a separate code fragment.

Instead, we give comments for differences.

A NEW HYBRID GENETIC ALGORITHM FOR MAXIMUM INDEPENDENT SET PROBLEM

315

Figure 2: Heuristic independent crossover (HIX).

In repair operator algorithm, in a WHILE-DO loop,

we successively remove vertices, with the largest

degrees (in contrast to crossover operator) being

considered first, from the child solution until a

feasible solution is achieved. This simple greedy

approach guarantees to always produce a feasible

solution for MISP.

2.5 Algorithmic Outline

The outline of the GA heuristic which we have

developed for MISP is shown in Figure 3.

Note that, as shown in code fragment, in each

iteration of WHILE-DO we select the best (most

near to optimum) solution from the current

population and keep it and waiting for next

generation individuals, In order to update this value.

At end, we return the best solution from the last

generation.

3 EXPERIMENTAL RESULTS

For experiment, we have used population size µ ≤

20, because HIX converges faster to optimum

solution, so no far more population size is needed.

As we said earlier, our parent selection method is

like steady state one and we evaluated each

individual by formula (1). On each instance graph,

we have run our algorithm 100 times.

First, we have tested MIS-HGA with two

problem challenging instances presented in Khuri

and Bäck (1994), called "misp101" and "misp202",

and compared our results with an efficient algorithm

ones represented there, called GENEsYS. We got

surprising results compared to Khuri and Bäck

(1994). Due to our heuristic crossover (HIX): for

"misp101" and "misp202", our range of solution

quality has been reduced to from 44 to 50 and from

90 to 98 respectively, while this range varies from

40 to 50 and from 90 to 98 for corresponding

instances in Khuri and Bäck (1994), respectively.

More importantly, in the latter case, we got one

appearance of value 98 which is one step nearer to

optimum solution. Our results are compared with

Khuri and Bäck (1994) in Table 1 and Table 2. N

indicates the values obtained.

Then we have tested a variety of benchmarks

with various numbers of vertices and edge density.

These instances are online available from Sloane

(2009). Results are summarized in Tables 3, 4 and 5.

We can see, in most cases that we got the optimum

solution, except very a few instances (which are

challenging ones), in which we got very near to

optimum solutions consistently.

Figure 3: The outline of our proposed GA.

Table 1: Comparison of Back's results with MIS-HGA's

results for Graph "misp101" which has a MIS = 52. f

indicates the Average Fitness.

HGA:-Algorithm MIS

t ← 0;

initialize population P

randomly;

WHILE t < numOfGenerations DO

BEGIN

evaluate P

using fitness function;

keep ( bestFounSoFar );

select best 50 % individuals from P

and put

them in P

t+1

;

FOR m=0 TO µ STEP 2 DO

BEGIN

select m

and (m+1)

individuals from P

;

temp ← HIX (m , m+1 );

ofs ← Mutate (temp);

Repair (ofs) and put it on P

t+1

after repair;

END

t ← t + 1;

END

Return bestFoundSoFar from P

numOfGeneratins

;

Algorithm HIX:

V' = {};

S = {v

∈ V : v ∈ P

or v

∈

};

Sort S in increasing order by the degree of its

elements;

WHILE S has more vertices DO

BEGIN

Select next (lowest-degree) vertex, say v

, from

S. in case of that more than one such v

found,

select one which has more frequency in P

and

. Break ties randomly for this case. Remove

, and:

V' = V' ∪ v

;

S = S – { u : u is an adjacent vertex for v

};

END

Return V';

ICSOFT 2009 - 4th International Conference on Software and Data Technologies

316

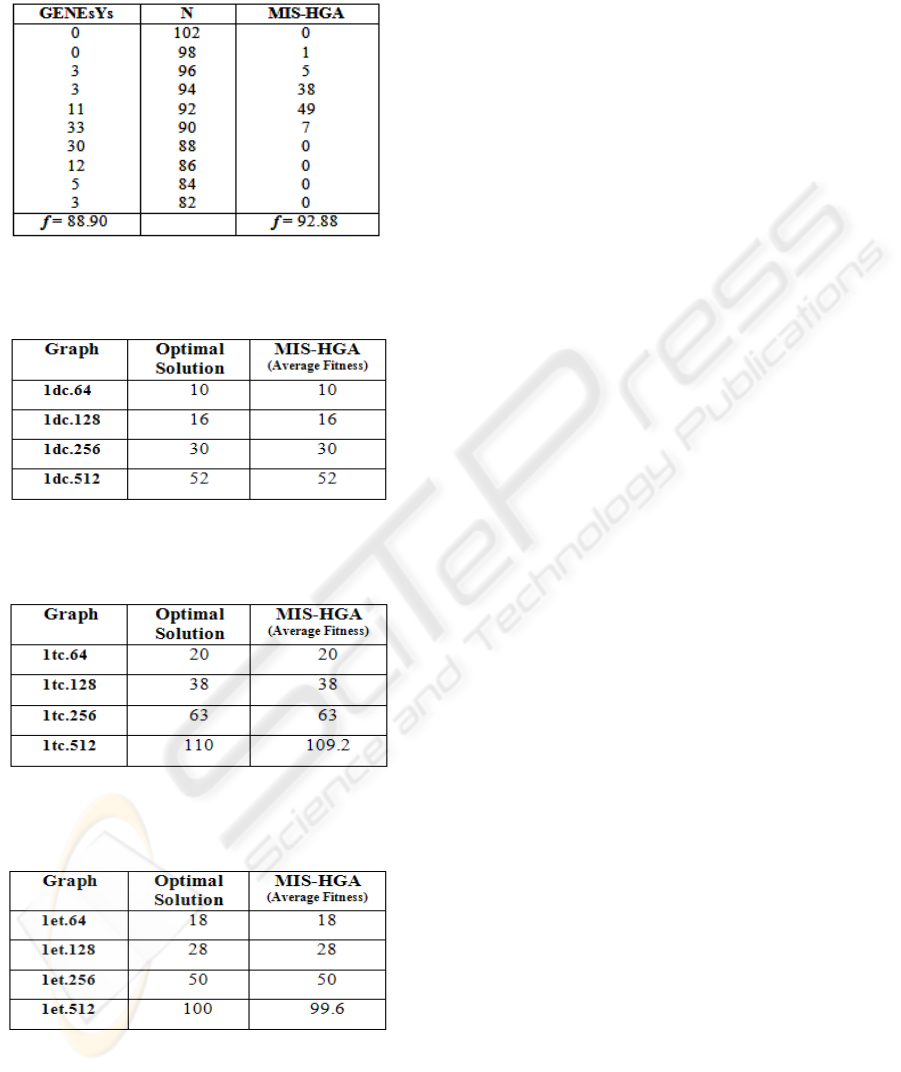
Table 2: Comparison of Back's results with MIS-HGA's

results for Graph "misp202" which has a MIS = 102. f is

defined as previous table.

Table 3: Experimental results obtained by MIS-HGA for

"1dc.*" graph instances. 100 runs of MIS-HGA are

performed.

Table 4: Experimental results obtained by MIS-HGA for

"1tc.*" graph instances. 100 runs of MIS-HGA are

performed.

Table 5: Experimental results obtained by MIS-HGA for

"1et.*" graph instances. 100 runs of MIS-HGA are

performed.

4 CONCLUSIONS

In this work, we have presented a hybrid genetic

algorithm for solving maximum independent set

problem. Most of the components of our GA are

comparable to those used in a standard GA. We have

demonstrated how a simple heuristic approach

applying to GAs can obtain far better results than

classical GAs. On a wide range of graph instances,

we have shown that the MIS-HGA is capable of

obtaining most high-quality solutions for problems

of various characteristics.

Our algorithm was directly compared with an

efficient existing evolutionary heuristic, called

GENEsYs, which is based on genetic algorithms.

Computational results show that the MIS-HGA gave

far superior quality solutions than this algorithm.

REFERENCES

Bodenhofer, U.: (2003) "Genetic Algorithms: Theory and

Applications". Lecture Notes. 3

edition.

Chu, P. C., Beasley, J. E.: (2004) "A Genetic Algorithm

for Set Covering Problem". European Journal of

Operational Research 94, 392-904.

Goldberg, D. E.: (1989) "Genetic Algorithms in Search,

Optimization and Machine Learning". Massachusetts:

Addison Wesley.

Hifi, M.: (1997) "A Genetic Algorithm-based Heuristic for

Solving the Weighted Maximum Independent Set and

Some Equivalent Problems". J. of Operational Research.

Holland, J. H.: (1992) "Adaptation in natural and artificial

systems". MA: MIT Press.

Khuri, S., Bäck, Th.: (1994) "An Evolutionary Heuristic

for the Maximum Independent Set Problem". In

proceedings of the IEEE Conference on Evolutionary

Computation, vol. 2, 531-535.

Lio, X., Sakamoto, A., Shimamoto, T.: (1997) A Genetic

Approach for Maximum Independent Set Problems".

IEIC Transactions on Fundamentals of Electronics,

Communications and Computer Sciences, No. 3 pp.

551-556.

Mehrabi, S., Mehrabi, A.: (2009a) "A New Genetic

Algorithm for Multiprocessor Scheduling Problem",

(in Persian). In Proc. of the National Conference on

Software Engineering (NSEC'09), Tehran, Iran.

Mehrabi, A., Mehrabi, S.: (2009b) "A Genetic Algorithm

for Multiprocessor Task Assignment Problem with

Limited Memory". 14

International CSI Symposium

on Intelligent Systems and Soft Computing

(CSICC2009), Tehran, Iran. Submitted.

Papadimitriou, C. H., Steiglitz, K.: (1982), "Combinatorial

Optimization: Algorithms and Complexity". Prentice Hall.

West, D. B.: (2001) "Introduction to Graph Theory".

Prentice Hall, Inc.

Whitley, D.: (1995) "Modeling Hybrid Genetic

Algorithms", Genetic Algorithms in Engineering and

Computer Science. Wiley, 1995.

Neil J. A. Sloane.: (2009) Challenge Problems: Inde-

pendent Sets in Graphs, online available at: http://

www.research.att.com/~njas/doc/graphs.html

A NEW HYBRID GENETIC ALGORITHM FOR MAXIMUM INDEPENDENT SET PROBLEM

317