Implementation of a Modular Neural Network in a

Multiple Processor System on Chip to

Classify Electric Disturbance

Danniel Cavalcante Lopes, Rafael Marrocos Magalhães

Jorge Dantas de Melo and Adrião Duarte Dória Neto

Federal University of Rio Grande do Norte – UFRN, Natal, RN, Brasil

Abstract. This paper shows the effectiveness of a modular neural network

composed of multilayers experts trained with a hybrid algorithm implemented

in a multiprocessor system on chip. The network is applied on the classification

of electric disturbances. The objective is to show that, even a FPGA with hard-

ware restrictions, it could be used to implement a complex problem, when pa-

rallel processing is used. To improve the system performance was used four

soft processors with a shared memory.

1 Introduction

The artificial neural network has been utilized to solve larger number of engineering

problems, including the functions approximation [1], control as well as patterns clas-

sification [2]. The type of network, its architecture and its training algorithm are cho-

sen and evaluated according to dimension and complexity of the problems. Scientists

have been researching many learning machines methods, including committee ma-

chines, to solve complex problems [2, 3, 4].

The quality of energy provided by an electric system is one of the greatest point of

interest for concessionaire and electric energy consumers. The literature presents

distinct approaches in the acquisition, characterization and classification of disturbs

present in power grids. Among these contributions, could be included the application

of Souza et al. [5] utilizing multilayer perceptrons with resilient propagation

(RPROP) training algorithm in disturbance classification, the discrete wavelet trans-

form in characterization of voltage or current signals made by Machado et al. [6] and

the detailed analysis of the electric signal pre-processing influence in neural network

classifier [7].

At the same time the growth of the Field Programmable Gate Arrays (FPGA) ca-

pabilities, make them viable for the implementation of complete System-on-Chip

(SoC) solution on the resolution of some complex problems [8]. Even with this

growth, these systems have much less power of processing than a modern general

processor. So with this restriction, maybe a more complex problem could not be im-

plement at real time in a small FPGA. The goal of this work is take advantage of

ideas from parallel processing to increase the performance of the system.

Cavalcante Lopes D., Marrocos Magalhães R., Dantas de Melo J. and Dória Neto A. (2009).

Implementation of a Modular Neural Network in a Multiple Processor System on Chip to Classify Electric Disturbance.

In Proceedings of the 5th International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 59-68

DOI: 10.5220/0002253900590068

 SciTePress

Following this development perspective, this work reports a learning algorithm for

extend modular neural network and the results obtained and also shows an embedded

architecture where the algorithm was executed and its performance.

2 Modular Neural Network

Committee Machines are neural network structures that use a concept commonly

used: divided and conquer. This concept aims to divide a large and complex task in a

set of sub-tasks that are easier to be solved and then regrouped again. From that, the

committee machine could be defined, in summary, as a set of learning machine, also

called experts, whose decisions are combined to achieve a better answer than the

answers achieved individually, in other words, a machine with better performance.

In the last years one of the mains areas of learning machine is the characterization

of methods capable to build these committee machines. Them could be divided into

static and dynamic structures; the modular network, as seen in Fig. 1, is a dynamic

type of committee. It is means that the input signal is used by the gating network to

build the global response.

Fig. 1. Modular Neural Network Diagram.

An advantage of modular networks when compared with other neural networks is

the learning speed. The learning processing is accelerated in problems where exist a

natural decomposition of the data at simple functions. To develop the committee

machine architecture and to implement the experts, was selected the multi layer per-

ceptron (MLP).

During the analysis and testing of the modular network presented by Jacobs and

Jordan [9], it was observed the structure was efficient for some simple problems. The

algorithm, when used with complex problems, is unable to found a good solution. So

we decided to use a larger architecture, for this, was opted to add hidden layers, as

well as MLP networks, and neurons with nonlinear activation function at both struc-

tures: experts and gating network. Also in each layer a bias was added. From the

parallelism standpoint, the adopted strategy was to involve an expert for each task, so

each MLP network is being treated by a unique processor. The committee machine

training, was conducted similarly to the MLP using backpropagation.

To train the modified modular network, was necessary to adjust the modular train-

ing algorithm. The way in which it was implemented enables to set, not only, differ-

ent architectures to each expert, but also specific values of the learning algorithm,

such as learning rates, momentum rate and delta-bar-delta parameters. Its possible, if

desired, assign independent training sets to each expert network. A brief description

from this algorithm is shown below

2.1 Hybrid Algorithm

To train the modified modular network was developed an algorithm adapted accord-

ing to Jacobs and Jordan [8] algorithms, for the model of Gaussian mixing associative

and also the error back propagation algorithm, by including the calculation of the

descend gradient. This algorithm is briefly described along this section, more details

and the complete algorithm is described at Magalhães et al. [10].

The modular network used is consisted by K MLP experts, with L

esp

layers with q

neurons in each layer. And also a gating network of the type MLP with L

pas

layers

with q neurons in each layer. The neurons activation functions in all networks can be

linear or non-linear. Was chosen the same architecture to all experts, to simplify the

implementation in hardware.

2.1.1 First Step

The first step of the algorithm is the calculation of a priori probability associated to

the i-th layer neuron output of the gating network, when from n-th application

example of training, obtained from (1)

()

exp u

PAS

(

)

(

)

exp

j=1

∑

PAS

()

(1)

where u

(l)

(n) is the i-th output neuron of the l-th layer from the gating network.

2.1.2 Second Step

The second step of the algorithm is to obtain the values of a posteriori probabilities

(n) associated to the output neuron i from the output of the gating network, when

from the n-th application example of training, obtained from (2)

()

exp −

||dn

()

− y

()

⎛

⎝

⎜

⎞

⎠

⎟

j=1

∑

()

exp −

||dn

()

− y

()

⎛

⎝

⎜

⎞

⎠

⎟

(2)

where d(n) is the expected answer and ye

(k)

(n) is the answer provided by the neuron i

from the layer l of the k-th expert for the example n.

2.1.3 Third Step

The third step is where are made increment in synaptic weights of the modular net-

work with multiple layers. The synaptic weights from the networks experts are up-to-

dated according to the equation (3)

()

(

)

(

)

(

)

nynnwnw

)1()()()(

−

+=+

ηδ

(3)

where η is the learning rate, and δ

(l)

(k) the gradient for the output layer neurons and

and y

is the output of the j neuron of the l-1 layer.

The synaptic weight increment from the gating network is done through (4)

n +1

()

(

)

(

)

−

(

)

(4)

To validate the algorithm we choose the problem of quality of energy, which is a

interest point for energy concessionaire. The application implemented on the system

architecture was a pattern classification for power lines disturbances. The methodolo-

gy of the application and data files and information were the same present in Medei-

ros et al. [7] study. This application evaluated the performance of an intelligent sys-

tem classifier, in this case a modular network, in electric disturbances classification.

The approach is done into four mains steps: getting the signal, pre-processing, de-

finition and classification of descriptors. The first step, which comes to obtaining the

electrical signals, has been carried out through the oscillograph network of São Fran-

cisco hydro Electric Company (CHESF) and also from the simulation via Transient

Alternative Program (ATP). The network consists of 370 oscillographs operation

with a sampling rate ranging between 20 and 256 samples/cycle. The signals used in

this study were collected in voltage lines levels of 69, 230 and 500kV, with a rate of

128 samples/cycle during 14 cycles [13]. These steps are described with more details

by Medeiros et al. in [7].

The pre-processing stage is to suggest descriptors that characterize the signs varia-

tions when diverted from a certain standard. The third step, which deals with the

descriptors definition, is performed from the decomposition of signals from the pre-

vious step. Following obtaining the descriptors, four disturbances classes are defined:

Voltage Sag, Voltage Swell, Harmonics and Transitories. The Final Step, the classifi-

cation, is performed by the application of classifiers based on artificial neural net-

works. Several architectures were tested, as shown at Table 1.

To the classification step were used two sets of data, the first for the training at

computer, and the second for validation at FPGA. The training set consisted by 800

patterns formed by the four disturbances classes.

To validate the modular network are used 344 input patterns with their respective

expected responses, consisting only of data obtained from the oscillographs.

Table 1. Modular Neural Network Architecture.

Net MOD-0 MOD-1 MOD-2 MOD-3

Number of Experts 3 3 3 3

Expert Architecture 10:3:4 10:5:4 10:10:4 10:15:4

Gating Architecture 10:5:4 10:5:4 10:10:4 10:15:4

Classification 98,46% 99,48% 100% 100%

From Table 1 it can be said that the modular neural network with the proposed al-

gorithm reaches a high amount of accuracy, approximately 100%.

More details of the algorithm implementation, information about performance and

a comparative with others neural net architectures are founded at Magalhães [10].

3 Multiple Processors Systems

The idea of parallel processing is not new. A parallel system is made by processing

elements (PE) that work in cooperation to solve a problem [11].

Parallel systems can be classified, for example, by the data or instruction flow, us-

ing these criteria they could be divided by Flynn’s taxonomy into Single Instruction

Single Data (SISD), Multiple Instruction Single Data (MISD), Single Instruction

Multiple Data (SIMD) and Multiple Instruction Multiple Data (MIMD). Systems with

multiple processors are members of the last class, which has n PE working in parallel,

processing asynchronous tasks concurrently in order to, in a given time, complete the

task.

The MIMD class can be subdivided into two subclasses, according to memory

access, a system could use or not a shared memory. The main difference between

them is that when using the shared memory, all PE have access to the same memory,

while in the other each PE has its own memory. So we can see two paradigms for

performing communication between the processors: first, the use of a shared memory;

second, a message passing facility.

At the first paradigm, whereby more than one PE could access the same shared

memory address to execute the write and read operations, is necessary to protect this

block. For example, using a semaphore, this component not allows two processes

access the same memory address simultaneously, avoiding a conflict [12].

The second paradigm is the message passing. In this case, a PE uses an intercon-

nection network to send and receive messages, and so establish a communication with

other PE. In this configuration each processor has its own memory that it is accessed

only by itself. Bus, ring and mesh are examples of network topologies, which exist to

build the interconnection of a multiprocessor system. The choice of which network

will be used is made according with characteristics as: cost, performance and how

many nodes exist.

In our case, we used a shared memory communication; a Nios II processor was

chosen as our PE, All components are communicating though the Avalon bus. This is

designed to connect on-chip processors and peripherals together in a system on pro-

grammable chip (SOPC). Peripherals, that use this bus, could be divided into master

and slave the first is able to start data transfers, while the second only transfers data

when requested. The Nios II Processor is an example of a peripheral master, while a

shared memory is a peripheral slave. When more than one master interacts with a

same slave it is necessary an arbiter with an arbitration to determine which master

have access to it. The arbitration scheme used by the arbitrator is the round robin.

The Nios II is a soft processor developed by Altera and distributed together with

its FPGAs. These are equivalent to a microcontroller, and are used in many different

applications. The Nios II has a central processing unit (CPU), memory and peripher-

als on a single chip. This is a RISC processor for general use. Being a software pro-

cessor, you can add and configure peripherals to the Nios II, according with the ap-

plication. The core of the Nios II can be divided into three versions: economic, basic

and fast. The developer will choose the most appropriate for their application. The

fast core is designed for applications that require high performance. It has cache for

data and instructions, which improve, for example, the performance of applications

with a large amount of data. The basic version has no cache for data and its perfor-

mance is about 40% smaller than the fast version, so it should be used in applications

where high performance is not a necessary feature. The economic core is half size of

the basic version. It has only the necessary functions to be used with Nios II instruc-

tions set. This core is used in applications where it is required a simple logic control.

To use the shared memory it is necessary a mutex component, this ensure a mutual

exclusion (ME) coordinating the read and write operations. The mutex provide an

atomic test-and-set operation that allows a processor to test if the mutex is available

and if so, to acquire the mutex lock in a single operation. Without the mutex, a write

operation would normally require the processor to execute two separate operations.

To do that the mutex has two fields (registers). Each processor has a single identifier

(ID). Each mutex has a VALUE field and OWNER field. The VALUE field is always

accessible for a processor to read it. A read value of 0x0000 represents mutex availa-

bility. If the mutex is available the processor writes its ID in OWNER and a different

value of 0x0000 in VALUE. Upon acquiring the mutex the processor performs the

operation (write or read) and then finalizes releasing the mutex.

4 System Architecture and Results

Table 2. Configurations Tested.

Number of Processors Space in the FPGA (LE) Time to Generate (hh:mm:ss)

4 12170 (61%) 00:42:17

6 17845 (89%) 03:54:26

8 21146 (101%) error

To design the architecture and obtaining the results was used a Nios II development

kit with a FPGA Altera Cyclone EP1C20F400C7 within 20600 logic elements (LE).

To generate the parallel architecture, was used an IBM-PC Pentium 4 3.0GHz with

1Gb of RAM, several configurations with different numbers of processors were gen-

erated, but the size of the FPGA was the limiting factor in defining their number in

the system. Table 2 shows some of these configurations.

At Fig. 1, is possible to see, that the modular network, could be easily divide at

small tasks. For example, each expert could be a task, and so implemented at a differ-

ent processor, as well as the gating network and the sum function.

We made three kind of tests; first, the modular neural network implement one pro-

cessor, in a serial version, second a parallel version using two processors, and the last

one is a parallel version using four processors. We made tests with the message pass-

ing facility paradigm and the shared memory. We choose to use shared memory,

because it has shown a better performance in this type of problem. At Fig. 2, we

could see a diagram of the Modular Neural Network Parallel Algorithm divided in

four small tasks and implemented at four processors. Each expert was implemented in

a different processor, as well as the gating network with the sum function.

Fig. 2. Modular Neural Network Parallel Diagram.

We choose to implement the gating network and the sum function at the same pro-

cessor, because at this way we need one less communication. So the parallel algo-

rithm has two communications: first, one-to-all, where the master processor sends the

inputs to all slaves (experts); second, all-to-one, that each slave sends its output to the

master processor. In our case the master processor is where the gating network and

the sum function were implemented. At the next tables, it is possible to see tree algo-

rithms: Table 3 the serial algorithm, Table 4, at first column, the parallel algorithm

implement at two processors, and at Table 4, at second column, the parallel algorithm

implement at four processors.

Table 3. Serial Algorithm.

Begin Serial Algorithm P1

1. Read inputs and write at the memory

2. Calculate the Experts outputs

3. Calculate the Gating Network output

4. Calculate the General output

End Serial Algorithm P1

All the processors have the same program; the first instruction’s program is to

identify what processor is, to execute its part of the code. Each processor has its own

memory and could access a shared memory. The modular neural network executed at

the FPGA was the MOD-0 shown at Table 1, this network achieved 98,46% of classi-

fication accuracy. MOD-0 is a network with fewer variables so it could be executed

even in a small FPGA, as the Cyclone.

Table 4. Parallel Algorithm.

egin Parallel Algorithm P1

1. Read inputs and write at the shared memory

2. Calculate the Gating Network output

3. Wait the Experts outputs

4. Calculate the General output

nd Parallel Algorithm P1

egin Parallel Algorithm P2

1. Wait P1 write the inputs at the shared memory

2. Calculate the Experts Output

3. Write Experts Results

nd Parallel Algorithm P2

egin Parallel Algorithm P1

1. Read inputs and write at the shared memory

2. Calculates the Gating Network output

3. Wait the Experts outputs

4. Calculate the General output

nd Parallel Algorithm P1

egin Parallel Algorithm P2

1. Wait P1 write the inputs at the shared memory

2. Calculate the Expert 1 output

3. Write Expert 1 Results

nd Parallel Algorithm P2

egin Parallel Algorithm P3

1. Wait P1 write the inputs at the shared memory

2. Calculate the Expert 2 output

3. Write Expert 2 Results

nd Parallel Algorithm P3

egin Parallel Algorithm P4

1. Wait P1 write the inputs at the shared memory

2. Calculate the Expert 3 output

3. Write Expert 3 Results

End Parallel Algorithm P4

To measure the performance of the three algorithms we use a performance counter,

which is a component that counts how many clocks a program, and a section of it,

need to execute. The serial algorithm has three main functions, as seen in Table 3; a)

calculate the experts outputs, b) calculate the gating network output, and c) calculate

the global output. The time, which each one needs, is shown in percent, at Fig. 3. The

time necessary to read an input is insignificant when compared with the others, so it

was not considerate.

The function that needs more time is: experts output, so we decide to make parallel

this function at the parallel algorithm. In this it is necessary a flag to syncronize the

processors, because the global output only could be calculated after the others.

Another function was created, the output experts wait. The algorithm was divided as

follow: the master processor calculate the gating network and wait the results from

slaves processors, so even the master processor finish with the gating network it

needs to wait to calculate de global output. All slaves calculate the experts outputs

and send the answers to master. As the algorithm only terminates after the calculation

of the global output, the total time of this system is measured on the master.

Results with 2 processors are shown at Fig. 4, at this configuration one processor

is the master, and the second processor is the slave, that calculate all the experts

outputs. As the tasks of the slave needs more time than the master, this stay 26.41%

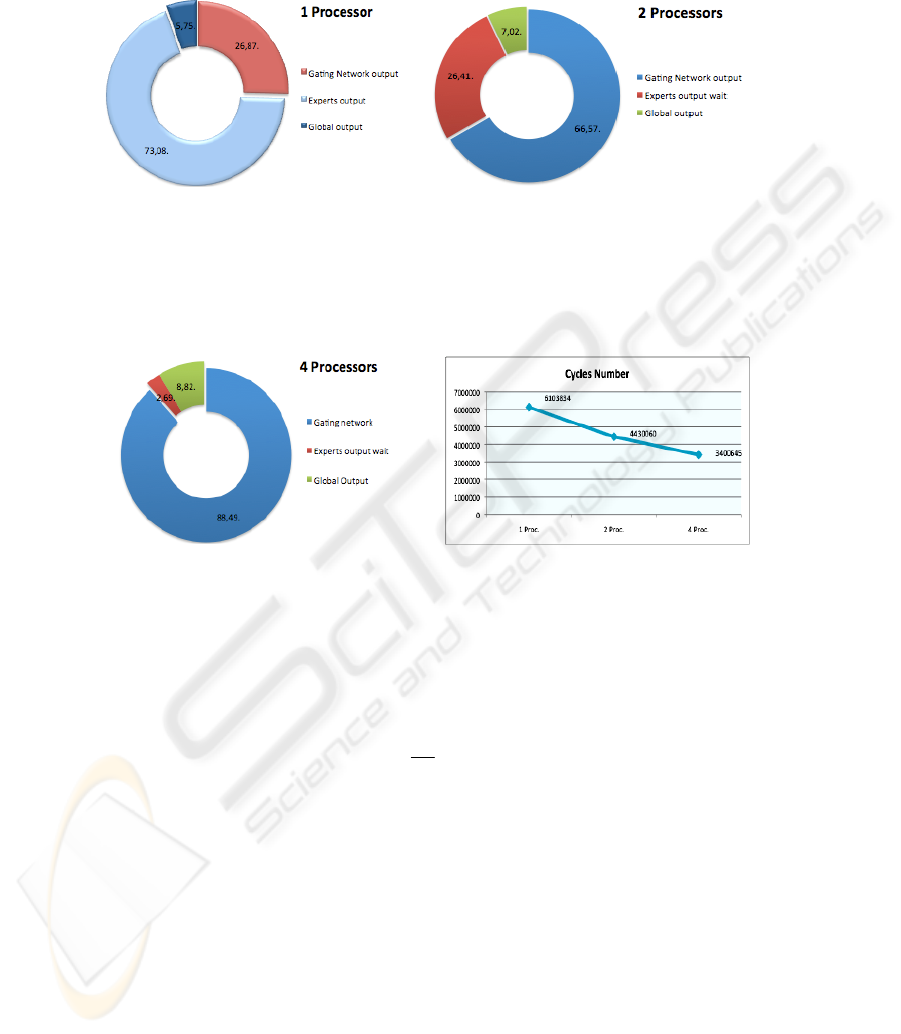
of time waiting the results from it. At the second configuration, in which has 4 pro-

cessors, each slave calculate the output of one expert, results are shown at Fig. 5.

Fig. 3. Time of each function at the

serial program.

Fig. 4. Time of each function at the maste

processor at the parallel algorithm with 2

processors.

With 4 processors the master stays only 2,69% of time at idle. The computing time

decrised at each improvement, this time, at number of clocks, is shown at Fig. 6.

Fig. 5. Time of each function at the

master processor at the parallel algo-

rithm with 4 processors.

Fig. 6. Total time, meseaured at cycles, o

each algorithm.

With the number of clocks of each algorithm, as shown in the figure above, it is

possible to calculate the speed-up of the parallel algorithm, this is obtained using the

expression (5).

G =

(5)

where T

is the serial execution time and T

is the parallel execution time. The speed-

up calculated was 1.47 for 2 processors, and 1.87 for 4 processors.

5 Conclusions

In this paper, the implementation of pattern classification for power lines disturbances

using multiple processors on FPGA was made. The classification achieved at MOD-0

was 98.46%.

We use a small Cyclone Altera FPGA, which has performance restrictions, to im-

plement the execution phase of the MOD-0. This operates at a frequency of 50MHz,

and has less than half size of new FPGA, even then the best speed-up achieved was

1.87, in other words, 93.5% of improvement at execution time.

This application is portable to different FPGAs, and could have the number of

processors easily increased due its scalability. Using a new one a better performance

could be achieving increasing the number of NIOS II inside it, and so execute the

MOD-1, MOD-2, MOD-3 networks and others applications more complex.

References

1. J. D. Melo, A. D. D. Neto, A. C. M. L. Albuquerque, R. L. S. Alves, “New Parallel Algo-

rithms for Back-propagation Learning”, Proceedings of IJCNN’02, Internacional Joint

Conference on Neural Networks Honolulu, USA 2002.

2. M. F. Medeiros Jr. and J. T. Oliveira and E. G. M. Lacerda and J.J.A.L. Leitão, “Distur-

bances Caracterization in Electric Energy Networks Using Second Generetion Wavelet

Transform”, VI Industry Application Conference – VI Induscon, Joinville – Sc, 2004.

3. D. Optiz and R. Maclin, “Popular ensamble methods: an empirical study”, Journal of Ar-

tificial Intelligence Research, vol 11, pp. 169-198, 1999.

4. G. Valentini and F. Masulli, “Ensemble of learning machines”, Neural nets WIRN Vietri-

02, Series Lectures Notes in Computer Sciences, Springer-Verlag, 2002.

5. B. A. Souza and N. S. D. Brito and W. L. A. Neves and R. B. Lima and S. S. B. Silva,

“Comparison between backpropagation and RPROP algorithms applied to fault classifica-

tion in transmission lines”, Proceedings of The International Joint Conference on Neural

Networks & International Conference on Fuzzy Systems, Budapeste, 2004.

6. R. N. Machado and U. H. Bezerra and E. G. Pelaes “Classification of signal with voltage

disturbance by means of wavelet transform and intelligent computacional techniques”,

WSEAS Transactions on Power Systems, v. 1, pp. 1538-1532, 2006.

7. M. F. Medeiros Jr and C. K. S. Santos and J. T. oliveira and P. S. M. Pires and J. D. Melo

and A. D. D. neto and J. J. A. L. Leitão, “Influence of signal processing in the Efficiency of

algorithms Based on Neural Networks for Disturbanc Classification”, Computacional Intel-

ligence in Image and Signal Processing, pp. 95 -100, 2007.

8. J. Castillo and P. Huerta and C. Pedraza and J. I. Martínez, “A Self-Reconfigurable Multi-

media Player on FPGA.” IEEE International Conference on Reconfigurable Computing and

FPGA’s – (ReConFig’ 06) – San Luis Potosí. México Pp. 1 – 6.

9. R. A. Jacobs and M. I. Jordan, “Adaptive mixtures of local expert”, Neural Computation,

volume 3, pp 79 – 87, 1991.

10. R. M. Magalhães and C. K. S. Santos and J. D. Melo and M. F. Medeiros, A. D. D. Neto,

“Application of a hybrid Algorithm in the Modular Neural Nets Trainning with Multilayers

Specialists in Electric Disturbance Classification”, Proceedings of International Conference

on Intelligent Engineering Systems, pp. 121-125, 2008.

11. K. Hwang and F. A. Briggs. “Computer Architecture and Parallel Processing.”, Singapore:

McGraw-Hill, 846p. McGraw-Hill series in computer organization and architecture, 1985.

12. Hübner, M; Paulsson, K; Becker, J. (2005), ”Parallel and Flexible Multiprocessor System-

On-Chip for adaptive Automotive Applications based on Xilinx MicroBlaze Soft-Cores”.

19th IEEE International Parallel and Distributed Processing Symposium (IPDPS’05) –

Denver, Colorado, USA. Pp. 149 – 154, 2005.