
APPLYING FINANCIAL TIME SERIES ANALYSIS TO THE
DYNAMIC ANALYSIS OF SOFTWARE
Philippe Dugerdil and David Sennhauser
HEG, Univ. of Applied Sciences of Western Switzerland, 7 route de Drize CH-1227 Geneva, Switzerland
Keywords: Reverse engineering, Dynamic analysis, Time series, Moving average, Class coupling.
Abstract: Dynamic analysis of programs is one of the most promising techniques to reverse-engineer legacy code for
software understanding. However, the key problem is to cope with the volume of data to process, since a
single execution trace could contain millions of calls. Although many trace analysis techniques have been
proposed, most of them are not very scalable. To overcome this problem, we developed a segmentation
technique where the trace is pre-processed to give it the shape of a time series of data. Then we apply
technical analysis techniques borrowed from the financial domain. In particular we show how the moving
average filtering can be used to identify the “trend” of the involvement of the class in the execution of the
program. Based on the comparison of the “trends” of all the classes, one can compute the coupling of
classes in order to recover the hidden functional architecture of the software.
1 INTRODUCTION
Legacy software system reverse-engineering has
been a hot topic for more than a decade. In fact, it is
well known that maintenance represents, by far, the
largest part of the software cost (Murphy, 2006).
Moreover, the biggest factor in these costs is
represented by the understanding of the software. In
other words, maintenance is largely a software
understanding problem. A necessary approach to
understand large complex system such as software is
to decompose it into quasi-decoupled sub-systems or
components (Simon, 1996) that represent its high-
level architecture. Therefore, many techniques have
been proposed to recover the high level architecture
from legacy code. Although the early approaches
dealt with the static analysis of the source code, such
as the well known fan in and fan out metrics of RIGI
(Muller et al., 1993), dynamic analysis techniques
have recently attracted much interest in the academic
community. The central idea behind these
techniques is to execute the legacy software
following its use-cases and harvest the time-ordered
list of methods or functions that have been executed:
the execution trace (Andritsos, Tzerpos, 2003). Most
of the time, the execution trace is stored in a file and
analyzed post mortem i.e. after the completion of the
execution. However, the biggest technical issue with
this approach is to deal with the large size of the
execution trace. Generally, for any industrial system
and real use-case, the execution trace is huge. For
example, in our experiments, the number of
functions calls (events) recorded amounted to
hundreds of thousands and even several millions.
But the information in such a file is highly
redundant. In case of loops or recursive calls for
example, the trace file may contain hundreds of
contiguous similar events or hundreds of contiguous
similar blocks of events. For an engineer to analyze
such a trace file, this enormous quantity of
information must be reduced. In the case of
frequency spectrum analysis (Andritsos, Tzerpos,
2003), the information is summarized by counting
the occurrences of similar events. In this case, the
quantity of data to interpret is bound by the number
of events considered. This is ok if the only
information one wants to extract is the global
frequency of the events. But this analysis is of very
limited use. Another way to reduce information is to
remove the redundancies using specific trace
compression techniques (Hamou-Lhadj, Lethbridge,
2002). Since the resulting file must be human
readable, it is not possible to use any standard
information theory-based compression algorithms.
In surmmary, the technique used must be tuned to
the purpose of the analysis. In our research, the
target is to identify the dynamic coupling between
194
Dugerdil P. and Sennhauser D. (2009).
APPLYING FINANCIAL TIME SERIES ANALYSIS TO THE DYNAMIC ANALYSIS OF SOFTWARE.
In Proceedings of the 4th International Conference on Software and Data Technologies, pages 194-201
DOI: 10.5220/0002255601940201
Copyright
c
SciTePress
classes to recover the functional architecture of the
legacy software. The functional architecture is the
structure of the components and their inter-
connections that implement some useful business
function (as represented by the use-cases). Two
classes are considered to be dynamically coupled if
they work closely together during the execution of a
use-case. But what does “working closely together”
really mean? A first approach could be to analyze
the “density” of calls between the instances of the
two classes. However, the calls are not always
direct. To overcome this problem many authors try
to identify recurring patterns of calls i.e. find the
sub-sequences of calls having the same structure.
But this search is known to be computationally
intensive therefore not very scalable. Moreover the
pattern finding approaches have a hard time taking
small variations of the patterns into account such as
polymorphic calls. For example, lets us have a class
A whose methods call the methods of class B
through an indirect call to methods of class C, that
are sometimes replaced by calls to the methods of
class D. In other words, the intermediate classes C
and D both implement polymorphic methods defined
in a common superclass. Then the pattern finding
algorithm will have problems identifying the
coupling of A and B, even if B is always involved
when A is called. The situation is worsened if the
methods of A call the methods of several classes
before calling the ones of B. But if the methods of B
are executed each time the methods of A are, we
understand that there is some strong coupling
between both classes. But the analytical
identification of such situation i.e. by checking
individual calls is computationally hard. Therefore
another approach must be found.
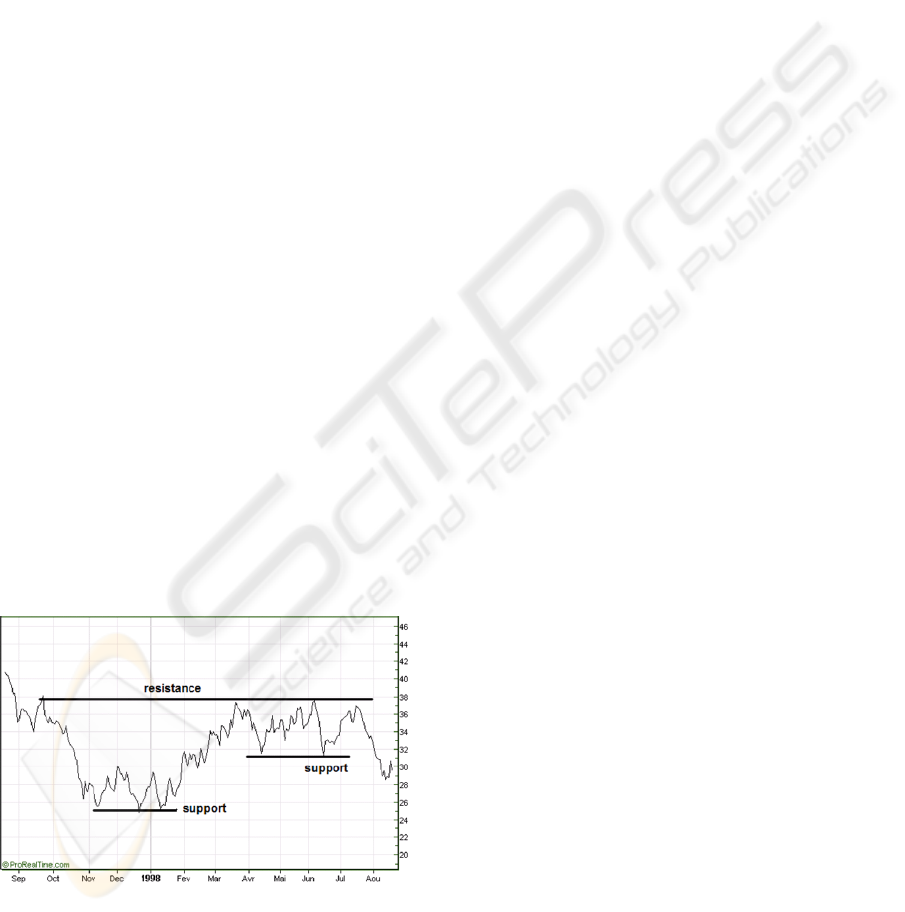
Figure 1: Stock price time series.
In fact, there is a domain where correlations
between events can be detected without exact
knowledge of the dependency chains between the
events: finance. In particular, one of the techniques
to identify stock price correlation is to analyze the
“shape” of their time series (Figure 1). This is
known as technical analysis (Bechu et al., 2008).
However, to apply these techniques to an execution
trace, we must transform it to a kind of time series of
data for each of the classes occurring in the trace.
This is done by segmenting the trace file into
contiguous trace segments. Then the occurrences of
the classes in each segment can be counted and
displayed as a time series (where time is defined by
the sequence of segments). From that basis, we can
apply time series filtering techniques to build our
dynamic correlation metrics. In section 2 we present
the details of the technique we used to get the
classes’ time series of data. Section 3 focuses on the
time series filtering and comparison techniques we
selected. Section 4 presents the experimental results
obtained using this technique and section 5 presents
the state of the art in trace analysis techniques.
Section 6 concludes the paper and presents future
work.
2 GENERATIN TIME SERIES
2.1
Introduction
The first step to dynamic analysis is to generate the
trace file. Although many techniques can be used
(Hamou-Lhadj, Lethbridge, 2004) we decided to use
code instrumentation. Then, instrumentation
statements are inserted in the source code of the
legacy system that is recompiled. This technique is
somewhat intrusive but has the advantage to be
applicable to any legacy programming language.
Some non intrusive techniques exist such as virtual
machine (VM) instrumentation but are limited of
course to languages that run on top of a VM. This is
not the case of most of the legacy programming
languages. Each of the recorded events must contain
at least the signature of the method called as well as
the name of the class in which it is defined. In case
of languages using module or package declarations,
the trace events must also record the package or
module in which the class is defined. Once the trace
file is generated (that could contain millions of
method calls or events), it is loaded into a database
for further processing.
2.2 Trace Segmentation
Once the trace is loaded in the database it is
segmented in contiguous segments and the number
APPLYING FINANCIAL TIME SERIES ANALYSIS TO THE DYNAMIC ANALYSIS OF SOFTWARE
195
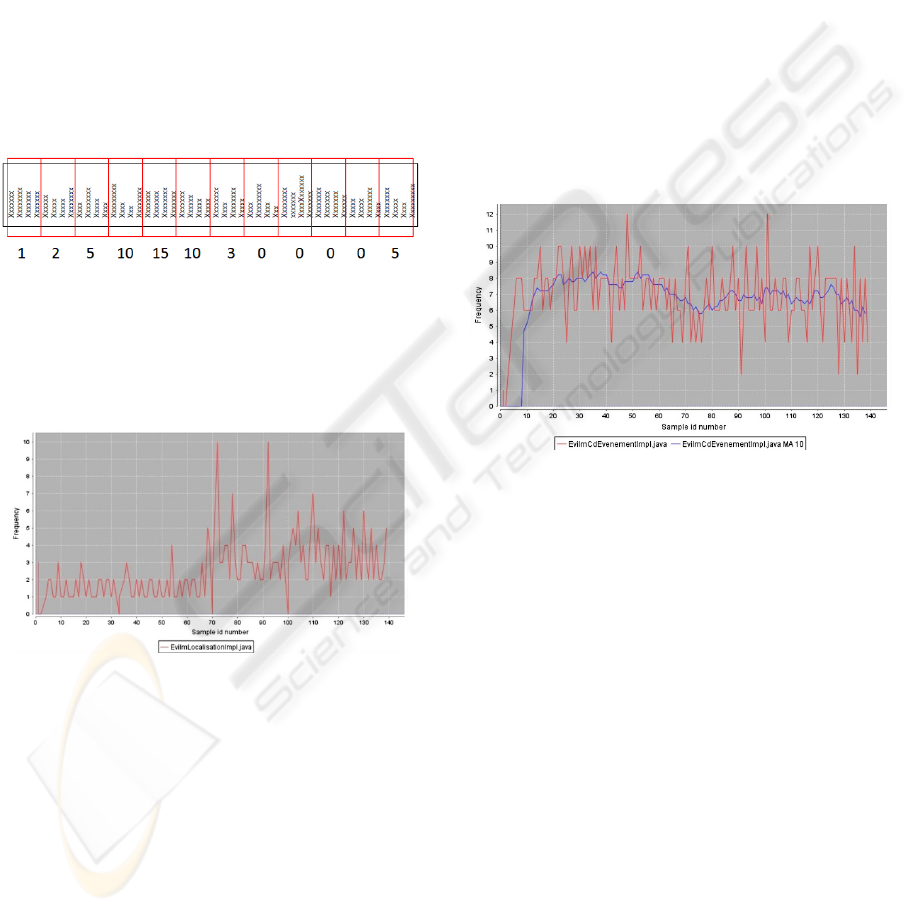
of occurrences of each of the classes is counted in
each segment. Figure 2 symbolically represents the
segmentation and occurrence counting of one class
in the execution trace. The trace file is represented
horizontally and each line in the file represents one
event (one method call). In this example, the class
investigated occurs 1 time in the first segment, 2
times in the second segment, 5 times in the third
segment and so on. This computation must be done
for each of the classes that occur at least once in the
trace file. The time series of a class is then
represented by the time-ordered sequence of
occurrences of this class in each of the trace
segments. After its computation, the time series is
stored in the database and can be displayed as a
graph as shown in figure 3.
Figure 2: Execution trace segmentation.
On the horizontal axis we represent the segment
number and on the vertical axis the number of
occurrences. We can observe that the shape of such
a curve is very “shaky”.
Figure 3: Class occurrence in the execution trace
represented as a time series of data.
3 TIME SERIES PROCESSING
3.1 Identifying Trends
Since the time series of any class shows a high
volatility (i.e. its graph representation is “shaky”), it
is difficult to compare it to the time series of another
class. Rather than comparing the rough curves it
would be much easier to compare the underlying
trends. This is the same as in finance where the
rough time series of stock prices are smoothed out
using mathematical operators to reveal patterns of
behavior. In particular the famous moving average
operator has proven to be very efficient at
identifying the macro trends. We then decided to use
this operator to analyze the time series of the classes.
The computation of the moving average is simple:
each value of the graph is the result of the
computation of the average of the n-1 previous
values plus the current one. This is known as the
order n moving average (n values are taken into
account to compute the present value). The result of
such a computation for the time series of a class is
presented in figure 4. The curve displayed in the
center of the figure is the filtered version of the
rough curve using a moving average of order 10.
Since the moving average must take the n-1 values
into account, it can only be displayed from the n
th
value.
Figure 4: Rough time series for a class and its filtered
counterpart based on the moving average.
We call filtered time series a class time series to
which we applied the moving average smooting
operator. Our experiments seem to suggest that the
comparison of two filtered time series is largely
insensitive to the number of segment in which we
split the execution trace. This is in sharp contrast
with our previous coupling measurement technique
that was based on the binary occurrence of the
classes in the segments (Dugerdil, 2007). In the
latter we only detect the absence (0) or presence (1)
of a class in the segments without taking into
account the actual number of occurrences. In other
words if a class occurs 1000 times or 1 time in a
given segment, the binary value for the class is 1 for
the segment. Then we compare the binary
occurrence of the classes among all the segments of
the execution trace to detect similarities. This binary
technique is very sensitive to the number of
segments in which we split the execution trace. This
is straightforward to understand. The widening of
the segment size could easily change the binary
ICSOFT 2009 - 4th International Conference on Software and Data Technologies
196
occurrence value from absent to present for a class
in a segment, since only 1 occurrence is enough. But
this change would not necessary happen to the other
classes it is coupled to, therefore changing the
coupling metrics. With our new technique based on
time series of data, the widening of the segment size
could lead to a bigger number of occurrences for a
given class. But this would probably also happen to
any class it is strongly coupled to, even if not to the
same magnitude. Moreover, we found that two
filtered time series for the same class computed with
different number of segments were very comparable
provided that we adapted the order of the moving
average when changing the number of segments. In
particular, we empirically observed that if we double
the number of segments, we must double the order
of the moving average to get similar trends for the
filtered time series of any class. The number of
segments in an execution trace must be set relative
to the number of classes occurring in the trace
(Dugerdil, 2007). We note NS(n) to mean that the
number of segments is n times the number of classes
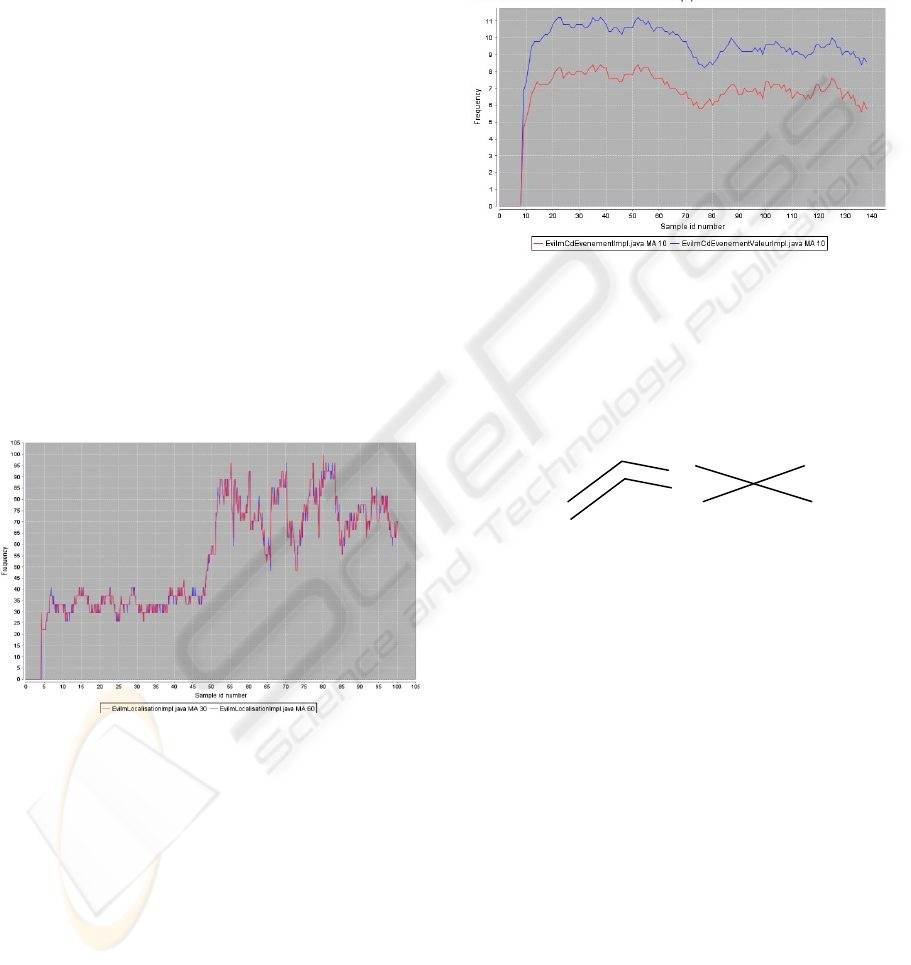
in the trace. As an example, figure 5 compares the
trends of the same class using two sets of
parameters: NS(5), Moving Average(30) and
NS(10), Moving Average(60).
Figure 5: Comparison of two time series of data for the
same class using different number of segments.
As can be seen in Figure 5, the two curves are
almost superimposed. To be able to display the
curves on the same scale we normalized the
horizontal axis to 100, whatever the number of
segments. But, the goal of our research is to compare
the time series of different classes to see if they are
dynamically coupled (if their “trends” are the same).
The first experiment with two different classes is
presented in Figure 6. We can see that the shape of
both curves display some similarities suggesting that
the classes might be coupled. To compute the
strength of the coupling of two classes, one idea is to
sum the absolute difference over all the segment of
the filtered time series of the two classes. But this
rough computation would lead to the same coupling
value for very different shapes of the time series. For
example, this technique would be unable to
distinguish between the two situations presented in
Figure 7.
Figure 6: Comparison of the time series of data of two
classes.
While the situation on the left part of the figure
could correspond to strongly coupled classes, this
would certainly not be the case for the situation
depicted on the right, although the absolute
difference would be the same.
Figure 7: Two very different situations leading to the same
coupling value.
To avoid such a problem we decided to compare
normalized time series where the occurrence value
in each segment is expressed as the percentage of the
maximum value for the time series. Therefore the
biggest value for any normalized time series is 100.
This idea has been applied to the curves presented in
Figure 6. The result is displayed in figure 8. We can
now clearly see that the shape of both curves is very
similar, in spite of the fact that their absolute values
were quite different. This may suggest some
moderate coupling between these two classes.
In contrast, figure 9 presents two classes whose
coupling is weak. The number of segments as well
as the order of the moving average is the same as in
the figure 8.
APPLYING FINANCIAL TIME SERIES ANALYSIS TO THE DYNAMIC ANALYSIS OF SOFTWARE
197
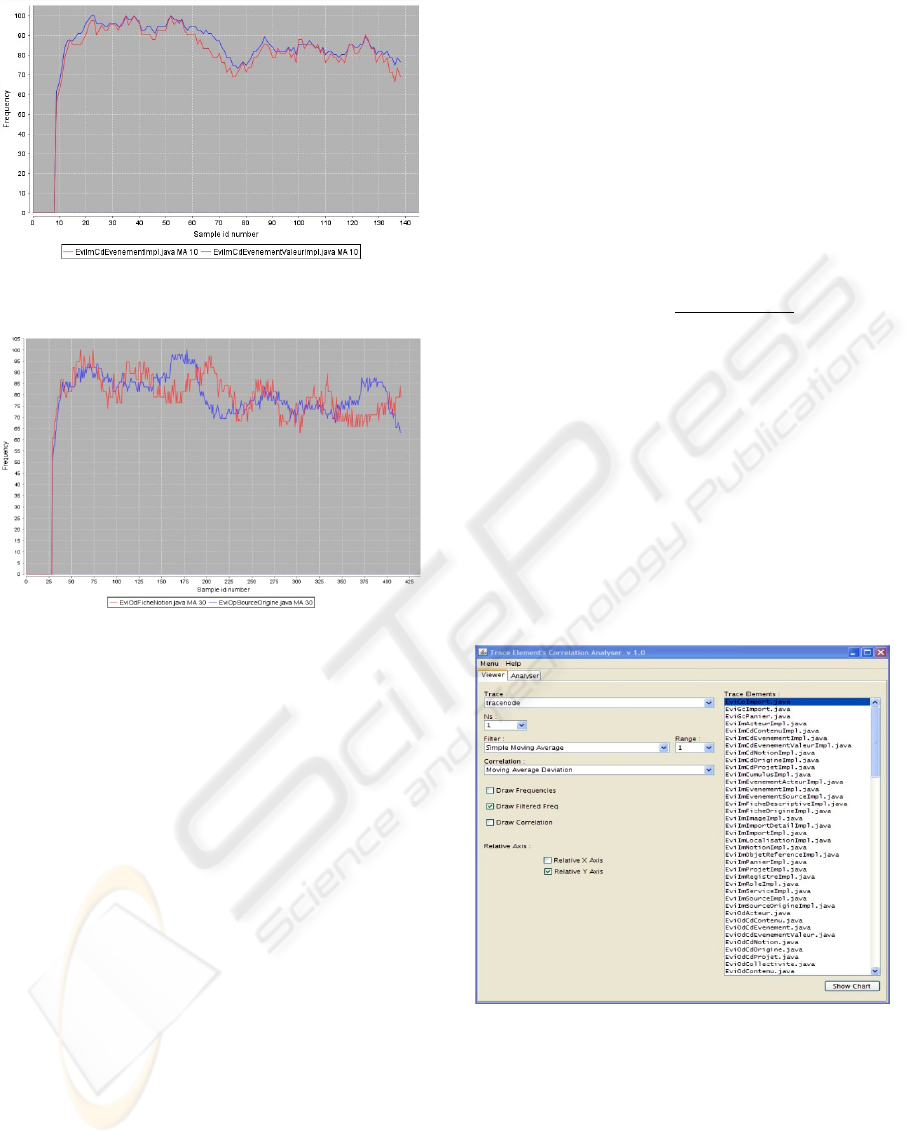
Figure 8: Filtered and normalized time series of two
moderately coupled classes.
Figure 9: Filtered and normalized time series of two
weakly coupled classes.
3.2 Computing Coupling Metrics
The coupling value between two classes is computed
as the sum of the absolute difference between their
filtered and normalized time series. The smaller the
coupling metrics, the higher the coupling between
the classes. Two perfectly coupled classes would
then have a coupling metrics of 0. However, there is
still a problem remaining: if the most of the values
of the two filtered time series is 0, the corresponding
coupling metrics would be small whatever the
coupling of the classes. To avoid this bias we
compute the average of the absolute difference over
all segments where at least one of the data of the
time series is not null. If both time series have 0 as
the value for some segment, we do not take this
segment into account. Formally the computation is
given by the following formulae. Let:
…
and
…
be two sets of values resulting from the filtering and
normalization of the time series of data for the
classes C
i
and C
j
respectively. The following is the
set of all pairs of values for the corresponding
segments, where at least one value is non zero.
,
,
0
0
Then, the number of segments for which at least one
value is non zero is the size of the previous set.
,
Therefore, the coupling metrics becomes:
,
∑|
|
4 EXPERIMENTAL RESULTS
To analyze the coupling between the classes we
developed a trace analysis tool that computes and
displays the time series of data of the classes as well
as the filtered and normalized curves. Then it
computes the coupling between any two classes and
shows the result as a list sorted by increasing value
of the coupling. In Figure 10 we present the control
panel of the trace analyzer.
Figure 10: The control panel of the trace analyzer.
In this panel we can select the execution trace to
analyze from the ones available in the database, set
the number of segments and the order (range) of the
moving average filter. On the right we can see the
list of classes present in the trace. From this panel
we can also launch the display of the time series of
data for any class or any set of classes. Next we can
switch to the coupling analysis panel where the
ICSOFT 2009 - 4th International Conference on Software and Data Technologies
198
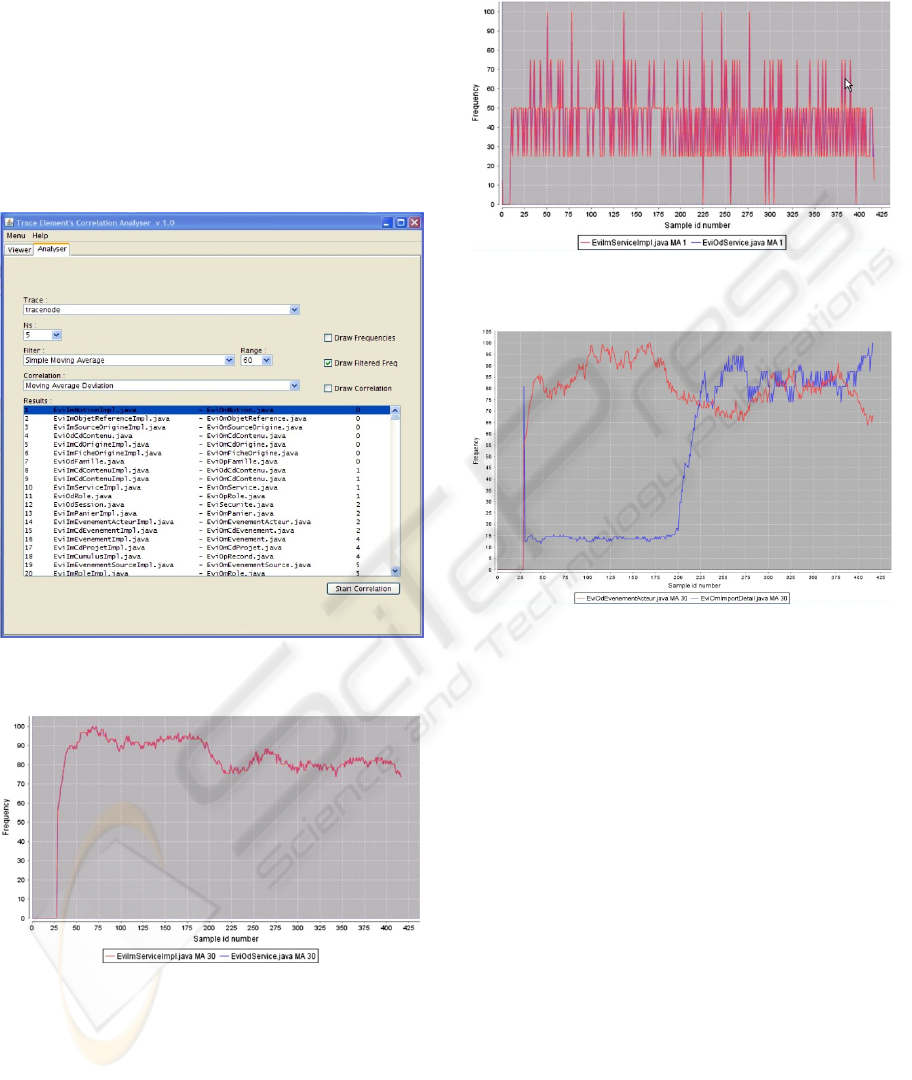
coupling between any pair of classes is displayed.
This is shown in figure 11 where we can see the list
of all pairs of classes, ranked in increasing number
of the coupling metrics. This example shows the
result of the analysis of a 600’000 events execution
trace with 139 classes. The parameters of the
analysis were NS = 5 and Moving Average order =
60. This analysis took about 4 min on a standard PC
(3GHz, 2GB Ram). In Figure 12 we present the
graph of two strongly coupled classes (coupling
value: 2). The two curves are indistinguishable.
Figure 11: The coupling metrics panel of the trace
analyzer.
Figure 12: Filtered and normalized graph of two strongly
coupled classes.
In comparison, we present in figure 13 the
unfiltered but normalized time series for the same
two classes as figure 12. Although we know from
our coupling measurement technique that the two
classes are strongly coupled, this is not evident from
the figure. As a final example, figure 14 present two
classes whose behavior is largely decoupled
(coupling value: 19398).
Figure 13: Unfiltered but normalized graph for the same
classes as figure 12.
Figure 14: Filtered and normalized graph for decoupled
classes.
5 RELATED WORK
In the literature, many techniques have been proposed
to recover the structure of a system by splitting it into
components. They range from document indexing
techniques (Marcus A., 2004), slicing (Verbaere,
2003), “concept analysis” technique (Siff, Reps,
1999) or even mixed techniques (Harman et al.,
2002). All these techniques are static i.e. they try to
partition the set of source code statements and
program elements into subsets that will hopefully help
to rebuild the architecture of the system. But the key
problem is to choose the relevant set of criteria (or
similarity metrics) (Wiggerts, 1997) with which the
“natural” boundaries of components can be found. In
the reverse-engineering literature, the similarity
metrics range from the interconnection strength of
RIGI (Muller et al., 1993) to the sophisticated
information-theory based measurement of (Andritsos,
Tzerpos, 2003, 2005), the information retrieval
APPLYING FINANCIAL TIME SERIES ANALYSIS TO THE DYNAMIC ANALYSIS OF SOFTWARE
199

technique such as Latent Semantic Indexing (Marcus,
2004) or the kind of variables accessed in formal
concept analysis (Siff, Reps, 1999) (Tonella, 2001).
Then, based on such a similarity metric, an algorithm
decides what element should be part of the same
cluster (Mitchell, 2003). In their work, Xiao and
Tzerpos compared several clustering algorithms based
on dynamic dependencies (Xiao, Tzerpos, 2005). In
particular they focused on the clustering based on the
global frequency of calls between classes. But this
approach does not discriminate the situations where
the calls happen in different locations in the trace.
This is to be contrasted with our approach that takes
the location of the calls in the trace into account. Very
few authors have worked on sampling or
segmentation techniques for trace analysis. One
pioneering work is the one of (Chan et al., 2003) to
visualize long sequence of low-level Java execution
traces in the AVID system (including memory event
and call stack events). But their approach is quite
different from ours. It selectively picks information
from the source (the call stack for example) to limit
the quantity of information to process. The problem to
process very large execution traces is now beginning
to be dealt with in the literature. For example,
Zaidman and Demeyer proposed to manage the
volume of the trace by searching for common global
frequency patterns (Zaidman, Demeyer, 2004). In
fact, they analyzed consecutive samples of the trace to
identify recurring patterns of events having the same
global frequencies. In other words they search locally
for events with similar global frequency. It is then
quite different from our approach that analyzes class
distribution throughout the trace. Another technique is
to restrict the set of classes to include in the trace like
in the work of (Meyer, Wendehals, 2005). In fact,
their trace generator takes as input a list of classes,
interfaces and methods that are to be monitored
during the execution of the program under analysis.
Similarly, the tool developed by (Vasconcelos et al.,
2005) allows the selection of the packages and classes
to be monitored for trace collection. In this work, the
trace is sliced by use-case scenarios and message
depth level and it is possible to study the trace per
slice and depth level. Another technique developed by
(Hamou-Lhadj, 2005) uses text summarization
algorithms, which takes an execution trace as input
and returns a summary of its main contents as output.
(Sartipi, Safyallah, 2006) use a patterns search and
discovery tool to separate, in the trace, the patterns
that correspond to common features from the ones
that correspond to specific features. Although the
literature is abundant in clustering and architecture
recovery techniques exploiting execution traces, most
of the approaches are analytical. The few paper
dealing with statistical approaches are still very
rudimentary.
6 CONCLUSIONS
The technique we presented in this paper is aimed at
computing the dynamic coupling between classes or
modules in legacy systems. The metrics is based on
the segmentation of the execution trace that let us
compute a time series of data for each class
occurring in the trace. The time series are then
filtered using the moving average technique,
borrowed from the technical analysis in finance. The
normalized result can then be used to compute the
coupling between any two classes. This represents
the key contributions of our work. In fact, none of
the published papers ever tried to segment the trace
to get another “perspective” on the trace analysis
problem. Our coupling metrics is used to identify
clusters of strongly coupled classes that represent the
functional components of the software. This metrics
has proven to be largely insensitive to the number of
segments. In fact, in the experiments we conducted
we saw that by changing the number of segments in
the trace, the order of the pairs of classes in the list
ranked by increasing coupling value stayed the
same. Only the coupling value changed slightly,
which is understandable since the number of
occurrences of the classes in each segment may
differ if the segment size is changed. Our technique
has the big advantage over analytical techniques (i.e.
the ones that analyze the individual events in the
trace) that it is very scalable. In fact, we were able to
analyze traces up to 7 millions of events without
trouble. So far, no techniques based on analytical
approaches for component identification have been
shown to be able to cope with such an amount of
data. Again, our method is successful because it
processes the trace using statistical technique rather
than analytical techniques. Clustering classes based
on their involvement in use-case implementation is
only the first step to recover the architecture of a
legacy system. The next step is to recover the
connections between the components using again the
coupling between the contained classes. Then not
only can, the coupling metrics, lead to the
identification of functional components, but also to
the identification of the connections between the
components. Therefore, our trace analysis technique
let us reconstruct the complete functional
architecture of the software. However the detailed
explanation of the architecture reconstruction
ICSOFT 2009 - 4th International Conference on Software and Data Technologies
200

technique goes beyond the scope of this paper. Our
current work focuses on the development of a series
of tool to leverage the component recovery system
presented in this paper. The first tool will display the
sequence diagram of the interaction between the
clusters (functional component). This will provide
us with a high level description of the sequence of
involvement of each cluster when executing the
system. Each cluster will then be matched against
the steps of the use-cases. Second, we are working
on a matcher to link the functional components to
high level features of the program. Third, we work
on 3D visualization to display the cluster formed
while executing the system. All these tools take
place in our reverse-architecting environment built
under Eclipse for legacy system understanding and
reengineering
REFERENCES
Andritsos P., Tzerpos V., 2003. Software Clustering based
on Information Loss Minimization. Proc. IEEE
Working Conference on Reverse engineering.
Andritsos P., Tzerpos V., 2005. Information Theoretic
Software Clustering. IEEE Trans. on Software
Engineering 31(2).
Bechu, T., Bertrand, E., Nebenzahl, J., 2008. L’analyse
technique : théories et méthodes. Paris : Economica.
Chan A., Holmes R., Murphy G.C., Ying A.T.T., 2003.
Scaling an Object-oriented System Execution Visualizer
through Sampling. Proc. of the 11th IEEE International
Workshop on Program Comprehension.
Dugerdil Ph., 2007 - Using trace sampling techniques to
identify dynamic clusters of classes. Proc. of the IBM
CAS Software and Systems Engineering Symposium
(CASCON).
Hamou-Lhadj A., Lethbridge T.C., 2002. Compression
Techniques to Simplify the Analysis of Large
Execution Traces. Proc. of the IEEE Workshop on
Program Comprehension.
Harman M., Gold N., Hierons R., Binkeley D. 2002. Code
Extraction Algorithms which Unify Slicing and Concept
Assignment. Proc IEEE Working Conference on
Reverse Engineering.
Hamou-Lhadj A., Lethbridge T.C., 2004. A Survey of
Trace Exploration Tools and Techniques. Proc. of the
IBM Conference of the Centre for Advanced Studies
on Collaborative Research.
Hamou-Lhadj A., 2005. The Concept of Trace
Summarization. Proc. of the 1
st
International
Workshop on Program Comprehension through
Dynamic Analysis.
Marcus A. 2004. Semantic Driven Program Analysis. Proc
IEEE Int. Conference on Software Maintenance.
Meyer M., Wendehals L., 2005. Selective Tracing for
Dynamic Analyses. Proc. of the 1
st
International
Workshop on Program Comprehension through
Dynamic Analysis.
Mitchell B.S., 2003. A Heuristic Search Approach to
Solving the Software Clustering Problem. Proc IEEE
Conf on Software Maintenance.
Muller H., Orgun M.A., Tilley S.R., Uhl J.S., 1993. A
Reverse Engineering Approach To Subsystem
Structure Identification. Software Maintenance:
Research and Practice 5(4).
Murphy Ph., 2006. Got Legacy? Migration Options for
Applications, Forrester Research.
Sartipi K., Safyallah H., 2006. An Environment for Pattern
based Dynamic Analysis of Software Systems. Proc. of
the 2
nd
International Workshop on Program
Comprehension through Dynamic Analysis.
Siff M., Reps T., 1999. Identifying Modules via Concept
Analysis. IEEE Trans. On Software Engineering 25(6).
Simon H., 1996. The Architecture of Complexity. In: The
Sciences of the Artificial (3rd edition). MIT Press.
Tonella P., 2001. Concept Analysis for Module
Restructuring. IEEE Trans. On Software Engineering,
27(4).
Vasconcelos A., Cepeda R., Werner C., 2005. An Approach
to Program Comprehension through Reverse
Engineering of Complementary Software Views. Proc.
of the 1
st
International Workshop on Program
Comprehension through Dynamic Analysis.
Verbaere M., 2003. Program Slicing for Refactoring. MS
Thesis, Oxford University.
Wiggerts T.A., 1997. Using Clustering Algorithms in
Legacy Systems Remodulari-zation. Proc IEEE
Working Conference on Reverse Engineering.
Xiao C., Tzerpos, V. , 2005. Software Clustering based on
Dynamic Dependencies. Proc. of the IEEE European
Conference on Software Maintenance and
Reengineering.
Zaidman A., Demeyer S., 2004. Managing trace data
volume through a heuristical clustering process based
on event execution frequency. Proc. of the IEEE
European Conference on Software Maintenance and
Reengineering.
APPLYING FINANCIAL TIME SERIES ANALYSIS TO THE DYNAMIC ANALYSIS OF SOFTWARE
201
