
ON THE CORRECTNESS OF SOFTWARE ARCHITECTURES
Formal Specification of Correctness Properties using π-AAL
Flavio Oquendo
European University of Brittany
University of South Brittany, VALORIA, BP 573, 56017 Vannes Cedex, France
Keywords: Software Architecture, Architecture Analysis Language, Structural and Behavioral Properties, Modal
μ-Calculus.
Abstract: Software has become a critical part of a rapidly growing range of products and services. Key aspects of the
development of such software-intensive systems are the description and analysis of their software architec-
ture, encompassing both the formal model of the component-based architecture and the formal specification
of the correctness properties that the modeled architecture must satisfy. Therefore, an Architecture Descrip-
tion Language (ADL) must be complemented by an Architecture Analysis Language (AAL) enabling the
specification of architecture-related correctness properties. A major challenge for an AAL is to provide
adequate expressive power to specify both structural and behavioral correctness properties, and to be well-
suited for machine-automated processing for verification, at a time. This paper presents how π-AAL com-
plements π-ADL (designed in the ArchWare European Project) for enabling the specification of architectur-
al correctness properties based on the modal π-calculus. The toolset and its experimentation in industrial
pilot projects are outlined.
1 INTRODUCTION
Software has become a critical part of a rapidly
growing range of products and services. Key aspects
of the development of such software-intensive sys-
tems are the description and analysis of their soft-
ware architecture, i.e. the fundamental organization
of the system embodied in its components, their re-
lationships to each other and to the environment,
and the principles guiding its design and evolution
(IEEE Std 1471-2000).
From the perspective of the system design, an
architecture description provides a formal model of
a software architecture in terms of its structure and
behavior:
The structure may be specified in terms of: (i)
components (units of computation of a system);
(ii) connectors (interconnections among compo-
nents supporting their interactions); (iii) configu-
rations of components and connectors.
The behavior may be specified in terms of: (i)
actions a component or connector executes or
participates in; (ii) relations among actions to
specify behaviors; (iii) behaviors of components
and connectors, and how they interact.
In the past decade, several Architecture Descrip-
tion Languages (ADLs) have been defined for mod-
eling the structure and behavior of software
architectures. However, describing the structure and
behavior of an architecture is needed, but it is not
enough. Indeed, in addition to describing software
architectures, designers need to rigorously specify
their correctness properties.
An architectural correctness property is a seman-
tic property that specifies a constraint which an ar-
chitecture must enforce to be correct with respect to
defined requirements. Thereby, an architecture is
correct when it, by its structure and behavior in
terms of configurations of components and connec-
tors, meets the functional and nonfunctional re-
quirements as described by the correctness
properties.
Before using an architecture description as a blu-
eprint to implement a system, designers must be able
to specify, validate and verify the correctness of the
architecture, i.e., that the architecture model satisfies
the specified correctness properties. In addition, as
the cost of addressing correctness properties is a
function of how late they are addressed (the later,
208
Oquendo F. (2009).
ON THE CORRECTNESS OF SOFTWARE ARCHITECTURES - Formal Specification of Correctness Properties using π -AAL.
In Proceedings of the 4th International Conference on Software and Data Technologies, pages 208-217
DOI: 10.5220/0002256302080217
Copyright
c
SciTePress

the more costly) (Barber & Holt 2001), addressing
them in the architectural phase leads to more cost-
effective solutions.
Therefore, an Architecture Analysis Language
(AAL) must complement (or be part of) an ADL in
order to enable the specification and support the
verification of architectural correctness properties. A
major challenge for an AAL is to provide sufficient
expressive power to specify both structural and be-
havioral correctness properties and to be well-suited
for machine-automated processing for verification,
at a time.
Formal methods are increasingly used for model-
ing software architectures (Marcos et al. 2007).
Their potential advantages have been widely recog-
nized (Oquendo 2007). Designing an AAL enabling
the specification of structural and behavioral cor-
rectness properties of component-based architec-
tures is a key research challenge.
π-AAL has been designed in the ArchWare
1
European Project to meet this challenge. It comple-
ments π-ADL and provides a uniform framework
for specifying correctness properties of software
architectures. These properties have different na-
tures: they can be structural (e.g., cardinality of arc-
hitectural elements, interconnection topology) or
behavioral (e.g., safety and liveness properties de-
fined on actions of the architectural elements’ beha-
viors).
The remainder of this paper is organized as fol-
lows. Section 2 introduces π-AAL design principles
and Section 3 the architecture description concepts
underlying π-ADL. Section 4 presents π-AAL con-
cepts and notation. Section 5 presents through a case
study how π-AAL can be used for specifying struc-
tural and behavioral correctness properties. In Sec-
tion 6, we compare π-AAL with related work and in
Section 7, briefly outline the π-AAL toolset and its
experimentation in pilot projects. To conclude we
summarize, in Section 8, the main contributions of
this paper and sketch future work.
2 DESIGN PRINCIPLES OF
π-AAL
π-ADL (Oquendo 2004) and π-AAL (Alloui et al.
2003) are companion languages for architecture
description and analysis, respectively. With π-ADL,
1
The ArchWare European Project has been partially funded by
the European Commission under contract No. IST-32360 in the
IST Framework Program.
architectures are described, expressing the structure
and behavior of their components, connectors, and
configurations. With π-AAL, correctness properties
that the architecture must satisfy in terms of struc-
ture and behavior of components, connectors, and
configurations are specified, enabling the analysis of
architecture models.
The following principles guided the design of π-
AAL:
π-AAL is a formal language: it provides a for-
mal system (at the mathematical sense) for
specifying correctness properties and reasoning
about them;
π-AAL is defined in a layered approach, with a
core canonical abstract syntax and formal se-
mantics;
π-AAL offers a user-friendly enhanced con-
crete syntax to be easily used by software sys-
tem architects.
π-AAL has as formal foundation the modal μ-
calculus (Kozen 1983), a calculus for expressing
properties of labeled transition systems by using
least and greatest fixed point operators. π-AAL is
itself a formal language defined as an extension of
the μ-calculus: it is a well-formed extension for de-
fining a calculus for expressing structural and beha-
vioral properties of dynamically communicating
architectural elements.
π-AAL takes its roots in previous work concern-
ing the extension of modal operators with data-
handling constructs (Mateescu & Garavel 1998), the
use of regular expressions as specification formal-
ism for value-passing process algebras (Garavel
1989), and the extension of fixed point operators
with typed parameters (Groote & Mateescu 1999).
Indeed, a natural candidate for “pure” behavioral
properties would be the modal μ-calculus, which is a
very expressive fixed point-based formalism sub-
suming virtually all temporal logics defined so far in
the literature (Stirling 2001). However, since π-AAL
must also provide features for expressing structural
properties of architectures, the modal μ-calculus is
not sufficient. Therefore, a formalism encompassing
both the predicate calculus and the modal μ-calculus
is needed. The π-AAL is, thereby, this encompass-
ing formalism.
π-AAL combines predicate logic with temporal
logic in order to allow the specification of both
structural and behavioral properties. It enables au-
tomated verification of property satisfaction by
model checking (through on-the-fly model check-
ing) and theorem proving (through deductive verifi-
cation).
ON THE CORRECTNESS OF SOFTWARE ARCHITECTURES - Formal Specification of Correctness Properties using
PI-AAL
209
3
3 ARCHITECTURE
DESCRIPTION WITH π-ADL
Software architectures can be described with π-ADL
which is a formal language based on the typed π-
calculus (Milner 1999; Sangiorgi 1992). One can
mechanically check whether an architecture de-
scribed in π-ADL satisfies a property expressed in
π-AAL.
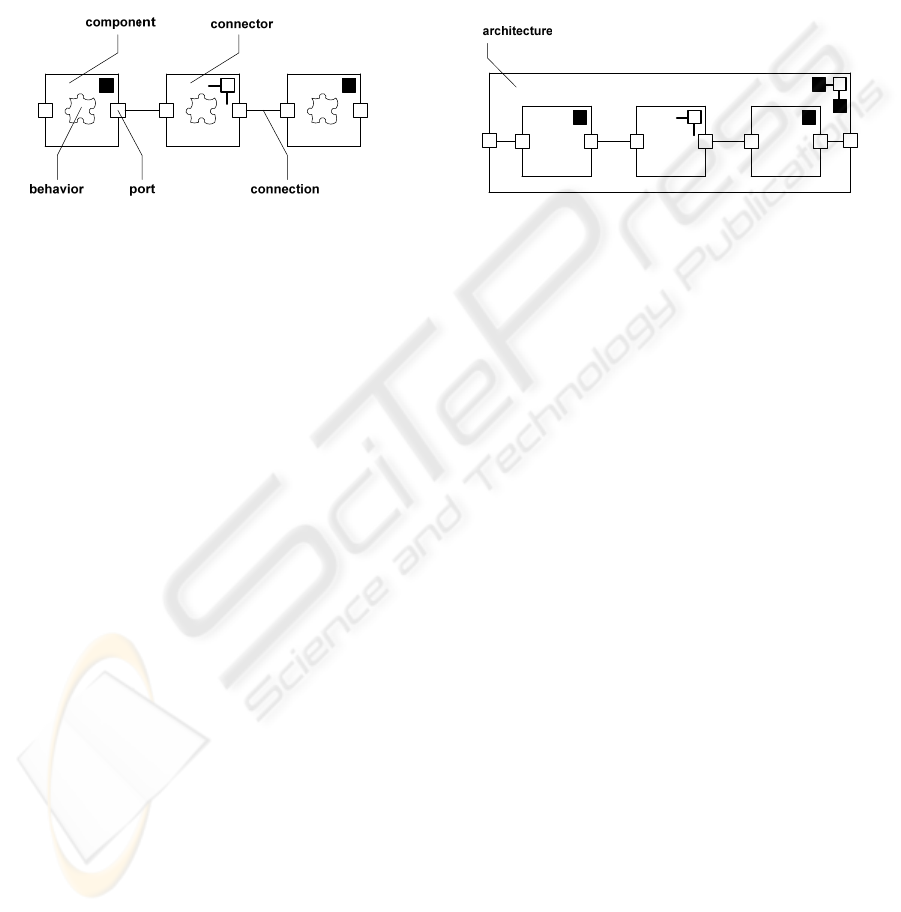
Figure 1: Architectural concepts in π-ADL.
In π-ADL, an architecture is described in terms
of components, connectors, and their composition.
Figure 1 depicts its main constituents.
Components are described in terms of external
ports and an internal behavior. Their architectural
role is to specify computational elements of a soft-
ware-intensive system. The focus is on computation
to deliver system functionalities.
Ports are described in terms of connections be-
tween a component and its environment. Their arc-
hitectural role is to put together connections
providing an interface between the component and
its environment. Protocols may be enforced by ports
and among ports.
Connections are basic interaction points. Their
architectural role is to provide communication chan-
nels between two architectural elements.
A component can send or receive values via
connections. They can be declared as output connec-
tions (values can only be sent), input connections
(values can only be received), or input-output con-
nections (values can be sent or received).
Connectors are special-purpose components.
They are described as components in terms of exter-
nal ports and an internal behavior. However, their
architectural role is to connect together components.
They specify interactions among components.
Therefore, components provide the locus of
computation, while connectors manage interaction
among components. A component cannot be directly
connected to another component. In order to have
actual communication between two components,
there must be a connector between them.
Both components and connectors comprise ports
and behavior. A connection provided by a port of a
component is attached to a connection provided by a
port of a connector by unification or value passing.
Thereby, attached connections can transport values
(that can be data or even connections).
Components and connectors can be composed to
construct configured composite elements, which
may themselves be components or connectors.
Figure 2: Architectural composition in π-ADL.
Architectures are composite elements
representing systems (e.g., see Figure 2). An archi-
tecture can itself be a composite component in
another architecture.
4 CORRECTNESS
SPECIFICATION WITH π-AAL
π-AAL supports analysis of component-based soft-
ware architectures, described with π-ADL. In π-
AAL, an architectural correctness property is speci-
fied in terms of logical formulas comprising: predi-
cate formulas, action formulas, regular formulas,
state formulas, and connection formulas. When eva-
luated, a formula is checked against the architecture
description, that provides the interpretation domain.
4.1 π-AAL Semantic Model
The formal foundation of π-AAL is the modal μ-
calculus extended with the predicate calculus. As
cited so far, π-AAL is itself a formal language de-
fined as an extended calculus subsuming the modal
μ-calculus and the predicate calculus for specifying
correctness properties on component-based software
architectures.
Formulas in π-AAL are formally interpreted
relative to a predicate-extended labeled transition
system.
Formally, a predicate-extended labeled transition
system (pLTS) is of the form pLTS = (StateSet,
ICSOFT 2009 - 4th International Conference on Software and Data Technologies
210

ActionSet, TransitionRelationSet, PredicateSetLa-
belling, state
0
), where:
StateSet is a non-empty set of states;
ActionSet is a set of actions (actions that label
transitions);
TransitionRelationSet is a set of transition rela-
tions, such that each transition relation transition
∈ TransitionRelationSet, is of the form transi-
tion ⊆ StateSet × ActionSet × StateSet;
PredicateSetLabelling : StateSet → 2
PredicateSet
is
a function that labels each state with the set of
atomic predicates true in that state (where Predi-
cateSet is the set of atomic predicates and
2
PredicateSet
the powerset of PredicateSet);
state
0
∈ StateSet is the initial state.
All states of StateSet are assumed to be reachable
from the initial state via sequences of (zero or more)
transitions of the TransitionRelationSet.
The actions action of ActionSet are defined as:
via connection send value
1
,…, value
n
via connection receive value
1
,…, value
n
where connection is a connection and value
1
,…,
value
n
are data values (base values or constructed
values).
In addition to communication actions, actions
can be internal to a component or connector:
the action unobservable, where unobservable ∉
ActionSet, is used to model an internal “unob-
servable” action of a component or connector
behavior,
the match action if, is used to express conditional
behaviors of components or connectors.
The predicates predicate of PredicateSet are de-
fined either as built-in predicates related to the arc-
hitectural structure, or as user-defined predicates.
Finally we can define BehaviorStateSet as the set
of states of a behavior in an architectural element
(e.g., component or connector). Therefore for all s ∈
BehaviorStateSet, PredicateSet contains all predi-
cates related to types and data declared in an archi-
tectural element expressed with π-ADL.
For a complete definition of the π-AAL semantic
model see (Alloui et al. 2003).
4.2 π-AAL Types
π-AAL is a typed language. It shares all base types
and type constructors of π-ADL equipped with their
operators. All types are value types. Value types are
base types or constructed types. Type environments
are expressed through declarations.
Typing
ValueType ::= BaseType | ConstructedType
BaseType ::= Any | Natural | Integer | Real | Boolean
| String | Behavior
ConstructedType ::= tuple [ ValueType
1
, …, ValueType
n
]
| view [ label
1
: ValueType
1
, …, label
n
: ValueType
n
]
| union [ ValueType
1
, …, ValueType
n
] | quote [ name ]
| variant [ label
1
: ValueType
1
, …, label
n
: ValueType
n
]
| location [ ValueType ] | sequence [ ValueType ]
| set [ ValueType ] | bag [ ValueType ]
| in [ ValueType ] | out [ ValueType ]
| inout [ ValueType ]
4.3 π-AAL Formulas
π-AAL provides the formula constructs for specify-
ing structural and behavioral properties to be satis-
fied by component-based software architectures.
The definition of π-AAL is structured in terms of
kinds of formula constructs:
predicate formula constructs for writing data
predicate formulas over a set of data values us-
ing data variables, data operators and predicate
operators;
action formula constructs for writing action pre-
dicate formulas over a set of connection and data
values;
regular formula constructs for writing regular
expressions (i.e., regular formulas) defined over
action formulas using regular operators;
state formula constructs for writing modal for-
mulas defined over regular formulas and value
variables using predicate, modal, and paramete-
rized fixed point operators;
connection formula constructs for writing formu-
la on connections as first-class elements, taking
into account connection mobility among archi-
tectural elements, i.e., components and connec-
tors.
4.4 Relating Properties to
Architectures
An architectural correctness property is specified by
a formula that may be a data predicate formula, an
action formula, a regular formula or a state formula.
Architectural properties are related to architec-
ture descriptions for specifying their correctness.
They are assumptions on the correctness of the ar-
chitecture model and state proof obligations.
Relating architectural properties to architecture
descriptions is defined as follows.
ON THE CORRECTNESS OF SOFTWARE ARCHITECTURES - Formal Specification of Correctness Properties using
PI-AAL
211

5
Relating Correctness Properties to Architectures
architecture { architectureDescription }
assuming { architecturalCorrectnessProperties }
5 CASE STUDY: CORRECTNESS
USING π-AAL
Instead of providing a formal description (Alloui et
al. 2003), we will present hereafter the use of π-
AAL for specifying correctness properties through a
case study of a typical component-based software
architecture, a pipe-and-filter architecture, described
in π-ADL.
Pipe-and-filter architectures, e.g., pipelines, are
used when a sequence of transformations is applied
to a stream of data by a sequence of filters, produc-
ing a final output. Hence, pipelines are pipe-and-
filter architectures composed of a single chain of
pipes and filters.
A pipe transmits output of one filter to input of
another filter. A filter transforms data received from
its input and sends the transformed data to its output.
Filters do not share state, i.e., they do not know
about upstream or downstream filters.
Figure 3: A simple pipeline architecture.
Figure 3 depicts a pipeline architecture compris-
ing two components (that are filters) which ex-
change data through a connector (that is a pipe).
5.1 Architecture Description
In a pipeline architecture:
the architecture is composed of filters and pipes;
filters are components;
a filter has a set of input and output connections
and uses a function to transform data;
pipes are connectors;
a pipe has a set of input and output connections
and transmits data from input to output as they
are;
a pipe connects two filters, it transmits an output
of a filter to an input of another filter.
Using π-ADL, the Filter component abstraction
can be formally described as follows.
component Filter is abstraction() {
type Data is Any.
port is {
connection input is in(Data).
connection output is out(Data)
} assuming {
protocol is {
( via input receive any. true*. via output send any )* }
}.
behavior is {
transform is function(d : Data) : Data {unobservable}.
via input receive d : Data.
via output send transform(d).
behavior()
}
}
Filter
The protocol is specified as a regular formula
built upon action predicates (one-step sequences) by
using the standard regular operators: ‘.’ (concatena-
tion), ‘|’ (choice), and ‘*’ (transitive reflexive clo-
sure). In these formulas ‘true’ means any action and
‘false’ no action.
The Pipe connector abstraction can be formally
described as follows.
connector Pipe is abstraction() {
type Data is Any.
port is {
connection input is in(Data).
connection output is out(Data)
} assuming {
protocol is {
(via input receive d : Data. via output send d)* }
}.
behavior is {
via input receive d : Data. via output send d.
behavior() } }
Pipe
This pipe is reliable. Let us now describe a pipe
that is unreliable, i.e., it can nondeterministically
choose either to transmit data correctly, or to lose it.
connector UnreliablePipe is abstraction() {
type Data is Any.
port is {
connection input is in(Data).
connection output is out(Data)
} assuming {
protocol is {
(via input receive d : Data. (via output send d | nil))* }
}.
behavior is {
via input receive d : Data.
choose {
via output send d. behavior()
or unobservable. behavior()
Unreliable
Pipe
A simple pipeline architecture, with two filters
ICSOFT 2009 - 4th International Conference on Software and Data Technologies
212

connected by one pipe as the one shown in Figure 3,
can be formally described as follows. It uses an un-
reliable pipe.
architecture OnePipeTwoFilters is
abstraction() { behavior is compose {
F1 is Filter()
and P is UnreliablePipe()
and F2 is Filter()
} where { F1::input as i1
and P::input unifies F1::output as o1
and P::output unifies F2::input as i2
and F2::output as o2
}
}
OnePipe
TwoFilters
A general pipeline architecture, with at least one
pipe and two filters, but with as many reliable pipes
and filters as needed, can be formally described as
follows.
architecture Pipeline is abstraction(n : Natural) {
behavior is compose {
F is sequence for i = 1 to n using Filter()
and P is sequence for i = 1 to n using Pipe()
} where {
iterate sequence(1..n) by i do {
P::i::input unifies F::i::output
and P::i::output unifies F::(i+1)::input }
}
} assuming {
parameter is { n >= 1 }
and F −> size >= 2
and P −> size >= 1
}
Pipeline
5.2 Specification of Correctness
Properties
Let us now specify with π-AAL different kinds of
architectural properties that must be analyzed in
order to guarantee the correctness of the architec-
ture, including architectural completeness and con-
sistency.
Architectural completeness means that the archi-
tecture description does not lack components, con-
nectors, connections or their parts or
interrelationships with respect to architecture-
specific, architect-defined, properties.
For instance, a pipeline architecture could be
considered to be complete if all pipes have their
input and output connections connected to filters
and all filters, but the first and last one, have their
input and output connections connected to pipes. Of
course, input connections must be unified to output
connections.
Regarding architectural consistency, it means
that the architecture description makes sense; that
different parts of the description do not contradict
each other. For instance, protocols of ports of uni-
fied connections must be compatible.
Regarding correctness, in addition to complete-
ness and consistency, it is defined with respect to the
correctness of the system features, i.e., the conformi-
ty with correctness requirements. For instance, all
filter transformations must be applied to all data.
Thereby, correctness (including completeness
and consistency) are semantic properties, and as so
are defined with respect to analysis of architecture-
specific, architect-defined, properties.
For instance, an architect could specify architec-
tural correctness properties for verifying that:
protocols of ports are projections of behaviors of
components or connectors;
protocols of unified ports are compatible, with
corresponding send-receive actions, and dead-
lock-free;
components, connectors, and the architecture are
deadlock-free;
ports of components and connectors in the confi-
guration are connected accordingly;
configuration of components and connectors
conform to the architectural style constraints.
More specifically, for the described pipeline ar-
chitecture, an architect could specify and verify if:
there is the right connectivity, in terms of the
pipeline style, among pipes and filters;
there is a safe alternation of send and receive
actions in components, i.e., in filters;
the pipeline is deadlock free;
there is an inevitable reachability of the trans-
form function after receive actions in the pipe-
line;
all data received in components and connectors
are transmitted.
Let us use the pipeline architecture and its com-
ponents and connectors described so far in π-ADL
to show how these properties could be specified
using π-AAL.
The concrete syntax of π-AAL is based on the
Object Constraint Language (OCL) and is part of a
UML Profile for π-ADL. The with construct intro-
duces the context for the property. The variable
declared in the with construct is used to refer to the
contextual instance. The “.”, “−>”, relational, logical
and collection operators have their usual meaning as
in OCL. Least and greatest fixed point operators
have their usual meaning as in modal μ-calculus.
The structural property “there is the right con-
nectivity, in terms of the pipeline style, among pipes
and filters” can be formally specified as follows. It
ON THE CORRECTNESS OF SOFTWARE ARCHITECTURES - Formal Specification of Correctness Properties using
PI-AAL
213

7
expresses that every pipe input port is connected to a
filter output port and every pipe output port is con-
nected to a filter input port in a pipeline architecture.
with { pl : Pipeline }
connectivityBetweenPipesAndFilters is property() {
-- every pipe input port is connected to a filter output port
-- and
-- every pipe output port is connected to a filter input port
pl.connectors −>
forall { p | p.ports.connections −>
forall { inp,outp |
pl.components −>
exists { fi, fo |
(fi.ports.connections union
fo.ports.connections) −>
forall { infi, outfo |
(p.ports.connections −> includes inp)
and (inp.type = input)
and (p.ports.connections −> includes outp)
and (outp.type = output)
and (fi.ports.connections −> includes infi)
and (infi.type = input)
and (fo.ports.connections −> includes
outfo)
and (outfo.type = output)
and (inp unifies outfo)
and (outp unifies infi)
}
}
}
}
}
The behavioral property “there is a safe alterna-
tion of send and receive actions in filters” can be
formally specified as follows. It expresses that there
is no send before a receive initially, no two consecu-
tive receives without a send in between, and no two
consecutive sends without a receive in between.
with { c : Filter }
safetyAlternation is property() {
-- no send before a receive initially
-- no two consecutive receives without a send in between
-- no two consecutive sends without a receive in between
c.ports.inputPrefixes −>
forall { r | c.ports.outputPrefixes −>
forall { s |
every sequence {
(not via r receive any)* . via s send any }
leads to state { false }
and
every sequence {
true* . via r receive any . (not via s send any)* .
via r receive any }
leads to state { false }
and
every sequence {
true* . via s send any . (not via r receive any)* .
via s send any }
leads to state { false }
}
The behavioral property “the pipeline architec-
ture is deadlock free” can be formally specified as
follows. It expresses that at any moment, the pipe-
line system can execute an action. Thereby, it is
never deadlocked.
with { pl : Pipeline }
deadlockFreedom is property() {
-- at any moment, the system can execute an action
pl.instances −>
every sequence { true* }
leads to state {
some sequence { true } leads to state { true }
}
}
The behavioral property “there is an inevitable
reachability of the transform data function after re-
ceive actions in a pipeline architecture” can be for-
mally specified as follows. It expresses that after a
receive action in a filter, the function transform will
always be carried out after a finite number of steps.
with { pl : Pipeline }
inevitableReachabilityOfTransformAfterReceive is
property() {
-- the inevitable reachability of a function transform data
-- after a receive
pl.components −>
forall { f | f.functions −>
forall { transf |
transf.name = transform implies {
f.ports.inputPrefixes −>
exists { r |
every sequence { true* . via r receive any }
leads to state {
finite tree Y given by {
some sequence { true } leads to state
{true}
and
every sequence { not via transf send any}
leads to state { Y }
}
}
}
}
}
}
The property “in a pipeline architecture, all data
received in components and connectors are transmit-
ted” can be formally specified as follows. It ex-
presses that every data that is received will be
eventually sent after a finite number of steps.
ICSOFT 2009 - 4th International Conference on Software and Data Technologies
214

with { pl : Pipeline }
dataTransmission is property() {
-- every data that is received will be eventually sent
-- after a finite number of steps
pl.components −>
forall { f | f.ports.inputPrefixes −>
forall { r | f.ports.outputPrefixes −>
exists { s | r.data −>
forall { d |
every sequence { true* . via r receive d }
leads to state {
finite tree Y given by {
some sequence { true }
leads to state { true }
and
every sequence {not via s send d }
leads to state { Y }
}
}
}
}
}
}
Now let us attach the architectural properties de-
fined above to the pipeline architecture described so
far.
architecture Pipeline is abstraction(n : Natural) {
behavior is compose {
F is sequence for i = 1 to n using Filter()
and P is sequence for i = 1 to n using Pipe()
} where { iterate sequence(1..n) by i do {
P::i::input unifies F::i::output
and P::i::output unifies F::(i+1)::input }
}
} assuming {
components −> forall { f : Filter | f.safetyAlternation()}
and connectivityBetweenPipesAndFilters()
and deadlockFreedom()
and inevitableReachabilityOfTransformAfterReceive()
and dataTransmission()
}
6 RELATED WORK
Several Architecture Description Languages (ADLs)
have been proposed in the literature (Medvidovic &
Taylor 2000), including: ACME, AESOP, AML,
CHAM-ADL, DARWIN, META-H, PADL,
RAPIDE, SADL, UNICON-2, and WRIGHT.
Most of these ADLs integrate or are coupled
with an Architecture Analysis Language (AAL),
e.g., ARMANI (Monroe 2001) extends ACME
(Garlan et al. 2000) for supporting the specification
of design constraints on the architecture structure;
and DARWIN (Kramer et al. 2003) embeds FSP for
supporting the specification of safety and (a limited
form of) liveness properties on the architecture be-
havior.
The main limitation of these AALs is that they
address either structural or behavioral properties, but
not both. Overall, they do not have the expressive
power to specify architectural correctness properties
such as those presented in this paper.
Indeed, π-AAL provides a novel language that
on the one side has been specifically designed for
architecture analysis taking into account the need to
specify and verify properties on both structure and
behavior from an architectural perspective and on
the other side is highly expressive. It allows the spe-
cification of both structural properties and behavior-
al properties concerning architecture descriptions
modeled in π-ADL.
Regarding behavioral properties, the choice of
the modal μ-calculus as the underlying formalism
provides a significant expressive power. Moreover,
the extension of μ-calculus modalities with higher
level constructs such as regular formulas inspired
from early dynamic logics like PDL (Fischer &
Ladner 1979) facilitates the specification task of the
practitioners, by allowing a more natural and con-
cise description of properties involving complex
sequences of actions. The extension of fixed point
operators with data parameters also provides a sig-
nificant increase of the practical expressive power,
and is naturally adapted for specifying behavioral
properties of value-passing languages such as π-
ADL.
In the context of software architectures, several
attempts at using classical process algebras and ge-
neric model checking technology have been reported
in the literature. In (Heisel & Levy 1997), various
architectural styles (e.g., repository, pipe-and-filter,
and event-action) are described in LOTOS, by using
specific communication patterns and constraints on
the form of components, and verified using the
CADP toolbox (Fernandez et al. 1996; Garavel et al.
2002). In (Rongviriyapanish & Levy 2000), several
variants of the pipe-and-filter style are described in
LOTOS and analyzed using CADP. In (Kerschbau-
mer 2002), the transformation of software
rchitecttures specified in LOTOS and their verifi-
cation using the XTL model checker (Mateescu &
Garavel 1998) of CADP are presented. Finally, an
approach for checking deadlock freedom of software
rchitecttures described using a variant of CCS is
described in (Bernardo et al. 2001).
All these works provide rather ad-hoc solutions
for a class of software architectures limited to static
communication between architectural elements.
None of them addresses dynamic architectures and
they can be subsumed by the more general frame-
ON THE CORRECTNESS OF SOFTWARE ARCHITECTURES - Formal Specification of Correctness Properties using
PI-AAL
215

9
work provided by π-AAL (with π-ADL) and its ve-
rification tools.
7 IMPLEMENTATION AND
EXPERIMENTATION
A major impetus behind developing formal languag-
es for architecture analysis is that their formality
renders them suitable to be manipulated by software
tools. The usefulness of an AAL is thereby directly
related to the kinds of tools it provides to support
automated verification. Indeed, π-AAL is supported
by a comprehensive analytical toolset composed of:
a model checking tool based on CADP;
a theorem proving tool implemented in XSB.
π-AAL (jointly with π-ADL) has been applied in
practice in several pilot projects in France, Italy,
UK, Switzerland, and China for designing compo-
nent-based software architectures. For instance, π-
AAL and its supporting toolset have been applied at
CERN (the European Organization for Nuclear Re-
search, Switzerland) for enforcing the correctness of
distributed control systems to restart particle accele-
rators.
Particle accelerators at CERN, as in many soft-
ware-intensive systems, are composed of a large
amount of distributed components, including nu-
merous sensors, actuators, processing and storage
devices. The CERN’s Technical Control Room de-
fined an architectural style with π-ADL and π-AAL
by formalizing all the correctness properties of sys-
tems controlling the restart of a particle accelerator.
These properties were embodied as a software envi-
ronment integrating the π-AAL toolset, in order to
guide the architectural design of such systems, ana-
lyze and generate the code of CERN’s particle acce-
lerator restart control systems.
This and other experimentations have shown that
π-AAL and its toolset are suitable for formally spe-
cifying and verifying structural and behavioral cor-
rectness properties of component-based software
architectures.
Furthermore, the ArchWare integrated develop-
ment environment itself (Oquendo et al. 2004) that
supports the architecture and development of soft-
ware-intensive systems using π-ADL and π-AAL is
itself a validation of π-ADL and π-AAL since it was
designed based on a component-based software ar-
chitecture and has been specified and developed
using these languages.
8 CONCLUSIONS AND FUTURE
WORK
This paper presented, in a nutshell, how π-AAL can
be used for specifying correctness properties of
component-based software architectures described
in π-ADL. It complements other publications on π-
AAL by providing a practical view on how to use its
concepts and notation for specifying correctness
instead of presenting its formal semantics.
π-AAL supports formal specification and corres-
ponding verification of both structural and beha-
vioral properties. This is a key factor in the
architectural design phase in order to support se-
mantic correctness.
Future work will mainly focus on specializing π-
AAL for Service-Oriented Architecture (SOA)
(OASIS 2008), a mainstream architectural style for
developing software-intensive component-based
systems based on the Web service technology stack,
in particular by refining the level of description and
analysis by providing service-oriented abstractions.
REFERENCES
Alloui I., Garavel H., Mateescu R., Oquendo F. (2003).
The ArchWare Architecture Analysis Language: Syn-
tax and Semantics. Deliverable D3.1b, ArchWare Eu-
ropean RTD Project, IST-2001-32360, January 2003,
URL: http://www-valoria.univ-ubs.fr/
ARCHLOG/ArchWare-IST/documents.htm
Barber K.S., Holt J. (2001). Software Architecture Cor-
rectness. IEEE Software, November/December 2001.
Bernardo M., Ciancarini P., Donatiello L. (2001). Detect-
ing Architectural Mismatches in Process Algebraic
Descriptions of Software Systems. Proceedings of the
2nd Working IEEE/IFIP Conference on Software Ar-
chitecture, Amsterdam, IEEE-CS Press, August 2001.
Fernandez J-C., Garavel H., Kerbrat A., Mateescu R.,
Mounier L., Sighireanu M. (1996). CADP (CAESAR/
ALDEBARAN Development Package) – A Protocol
Validation and Verification Toolbox. Proceedings of
the 8th International Conference on Computer-Aided
Verification, New Brunswick, USA, LNCS 1102,
Springer, August 1996.
Fischer M.J., Ladner R.E. (1979). Propositional Dynamic
Logic of Regular Programs. Journal of Computer and
System Sciences, Vol. 18, 1979.
Garavel H. (1989). Compilation and Verification of
LOTOS Programmes. PhD Dissertation, Univ. Joseph
Fourier (Grenoble), November 1989 (In French).
Garavel H., Lang F., Mateescu R. (2002). An Overview of
CADP 2001. European Association for Software
ICSOFT 2009 - 4th International Conference on Software and Data Technologies
216

Science and Technology (EASST) Newsletter, Vol. 4,
August 2002.
Garlan D., Monroe, R., Wile D. (2000). ACME: Architec-
tural Description of Component-Based Systems.
Foundations of Component-Based Systems, Leavens
G.T, and Sitaraman M. (Eds.), Cambridge Univ. Press,
2000.
Groote J. F., Mateescu R. (1999). Verification of Tempor-
al Properties of Processes in a Setting with Data. Pro-
ceedings of the 7th International Conference on
Algebraic Methodology and Software Technology,
Amazonia, Brazil, LNCS 1548, January 1999.
Heisel M., Levy N. (1997). Using LOTOS Patterns to
Characterize Architectural Styles. Proceedings of the
International Conference on Theory and Practice of
Software Development, LNCS 1214, Springer, 1997.
IEEE Std 1471-2000 (2000). IEEE Recommended Prac-
tice for Architectural Description of Software-
Intensive Systems, October 2000.
Kerschbaumer A. (2002). Non-Refinement Transforma-
tion of Software Architectures. Proceedings of the
ZB2002 International Workshop on Refinement of
Critical Systems: Methods, Tools and Experience,
Grenoble, January 2002.
Kozen D. (1983). Results on the Propositional μ-Calculus.
Theoretical Computer Science, Vol. 27, 1983.
Kramer J., Magee J., Uchitel S. (2003). Software Archi-
tecture Modeling and Analysis: A Rigorous Approach.
Formal Methods for Software Architectures, Springer,
LNCS 2804, 2003.
Marcos E., Cuesta C.E., Oquendo F. (Eds.) (2007). Spe-
cial Issue: Software Architecture. International Jour-
nal of Cooperative Information Systems (IJCIS), Vol.
16, No. 3/4, September/December 2007.
Mateescu R., Garavel H. (1998). XTL: A Meta-Language
and Tool for Temporal Logic Model Checking. Pro-
ceedings of the 1st International Workshop on Soft-
ware Tools for Technology Transfer, Aalborg,
Denmark, July 1998.
Medvidovic N., Taylor R. (2000). A Classification and
Comparison Framework for Architecture Description
Languages. ACM TOSEM, Vol. 26, No. 1, January
2000.
Milner R. (1999). Communicating and Mobile Systems:
The -Calculus. Cambridge University Press, 1999.
Monroe R. (2001). Capturing Software Architecture De-
sign Expertise with ARMANI. Technical Report
CMU-CS-98-163, Carnegie Mellon University, Janu-
ary 2001.
OASIS (2008). Reference Architecture for Service
Oriented Architecture, V. 1.0, OASIS Standard, 23
April 2008, URL: http://docs.oasis-open.org/soa-
rm/soa-ra/v1.0/soa-ra-pr-01.html.
Oquendo F. (2004). -ADL: An Architecture Description
Language based on the Higher Order Typed -
Calculus for Specifying Dynamic and Mobile Soft-
ware Architectures. ACM Software Engineering Notes,
Vol. 29, No. 3, May 2004.
Oquendo F. (2006). Formally Modeling Software Archi-
tectures with the UML 2.0 Profile for -ADL. ACM
Software Engineering Notes, Vol. 31, No. 1, January
2006.
Oquendo F. (Ed.) (2007). Proceedings of the European
Conference on Software Architecture (ECSA’07).
LNCS 4758, Springer, September 2007.
Oquendo F., Warboys B., Morrison R., Dindeleux R.,
Gallo F., Garavel H., Occhipinti C. (2004). ArchWare:
Architecting Evolvable Software. Software Architec-
ture. Software Architecture, LNCS 3047, Springer,
May 2004.
Rongviriyapanish S., Levy N. (2000). Variations on the
Pipe and Filter Architectural Style. Proceedings of
AFADL 2000
, Grenoble, France, January 2000 (In
French).
Sangiorgi, D. (1992). Expressing Mobility in Process Al-
gebras: First-Order and Higher-Order Paradigms.
PhD Thesis, University of Edinburgh, 1992.
Stirling C. (2001). Modal and Temporal Properties of
Processes. Springer, 2001.
ON THE CORRECTNESS OF SOFTWARE ARCHITECTURES - Formal Specification of Correctness Properties using
PI-AAL
217
