Topologies and Meaning Generating Capacities of

Neural Networks

Jürgen Klüver and Christina Klüver

Department of Economy - COBASC Research Group, University of Duisburg-Essen

Universitätsstr. 12, 45117 Essen, Germany

Abstract. The paper introduces the concept of meaning generating capacity

(MC) of neural nets, i.e. a measure of information processing, depending on the

size of basins of attraction. It can be shown that there is a significant relation

between the variance values of the weight matrix of a network and its MC-

values. By the concept of MC network characteristics like robustness and

generalizing capability can be explained.

1 Introduction

The analysis of topological characteristics of complex dynamical systems frequently

enables important insights into the behavior, i.e. the dynamics of such systems. By

“topology” we here mean that set of system’s rules that determine, which elements of

the respective systems interact with which other elements. In the classical

mathematical meaning of topology these rules define the neighborhood relations of

the respective elements, which are at the core of, e.g., the fundamental Hausdorff

axioms of topology. In the case of neural networks the topology is usually defined by

the according weight matrix, which determines the degree of interaction between the

different elements, including the limiting case of interaction degree equal to zero.

In [1] we introduced the concept of the meaning processing capacity (MC) of a

complex dynamical system. This definition was motivated by some informal remarks

of Wolfram [3] about the “information processing capacity” of complex dynamical

systems. With this term Wolfram described the fact that frequently different initial

states of a system generate the same final attractor state; other systems in contrast

generate different final states if the initial states are different. In other words, the

information processing capacity refers to the different sizes of the “basins of

attraction” of a system, i.e. the sets of initial states that generate the same final

attractor state.

In [1] we defined the concept of the “meaning” of a message by the final attractor

state a system generates when receiving this message; in other words, a system

processes a message and generates an according meaning. Therefore, we now use the

term of meaning generating capacity (MC), i.e. the capacity to generate more or less

different meanings when receiving different inputs.

The MC-value of a complex dynamical system is now defined as the proportion

between the size m of the set of all final attractor states and the size n of the set of all

Klüver J. and Klüver C. (2009).

Topologies and Meaning Generating Capacities of Neural Networks.

In Proceedings of the 5th International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 13-22

DOI: 10.5220/0002261600130022

 SciTePress

initial states of a system, i.e., MC = m/n. Obviously 0 < MC ≤ 1: MC = 0 is

impossible because each complex system has at least one final state, even if it is an

attractor state with a very large period. The according limiting case hence is MC =

1/n. If MC is very small then many different initial states will generate the same final

states – the according attractors are characterized by large basins of attraction. If MC

= 1 then each different initial state will generate a different final attractor state. This is

the other limiting case, where the basins of attraction all are of size 1. In other words,

small values of MC mean large basins of attractions and vice versa. It must be noted

that we refer only to discrete systems, i.e. systems with only a finite number of initial

states.

There are at least three main reasons why this concept is important: On the one

hand it is possible via the usage of MC to analyze complex dynamical systems like

neural networks with respect to their informational complexity. In this sense MC

allows for new approaches in the theory of computability. On the other hand an

important and frequently mentioned characteristic of neural networks can be

understood in a new and more differentiated way: In all textbooks on neural networks

there are statements like “one of the main advantages of neural networks is their

robustness, i.e. their tolerance with respect to faulty inputs” or something equivalent.

We shall show that via the definition of MC not only a theoretical explanation of this

advantage can be given but also a measurement of this robustness; in particular by the

variation of MC specific neural networks can be generated that are either very robust,

less robust or not at all robust in the sense of error tolerance.

Last but not least it is possible to give by the usage of MC an explanation for

phenomena known from the field of human information processing. It is well known

that different humans react in a significant different way to the same messages. This

can be illustrated by the examples of fanatics who refer all messages to the same

cause, e.g. the enmity of Western Capitalism to religious movements. The psychiatrist

Sacks [2] for another example describes a rather intelligent and well-educated man

who is unable to distinguish little children from fire hydrants. The definition of MC

can be a useful approach to construct mathematical models for the explanation of such

phenomena.

In contrast to dynamical systems like, e.g., cellular automata and Boolean

networks neural networks are not often analyzed in terms of complex dynamical

systems. Therefore, it is necessary to clarify what we understand by “initial states”

and “final attractor states” when speaking of neural networks.

In a strict systems theoretical sense all initial states of neural networks are the

same, i.e. the activation values of all neurons are equal to zero, and regardless to

which layer(s) they belong. Because this fact would make the definition of different

initial states quite useless we define the initial state of a neural net as the state where

the neurons of the input layer have been externally activated with certain input values

and where the activation values of all other neurons still are equal to zero, in

particular those of the output layer. An initial state S

of a neural net, hence, is

formally defined by S

= ((A

), (0)), if (A

) is the input vector and (0) is the output

vector, i.e. it denotes the fact that the values of the output neurons are still equal to

zero. If there is no specific input layer then the definition must be understood that

some neurons are externally activated and the others are not.

The external activation of the input neurons causes via the different functions the

“spread of information”, determined by the respective weight values. In the case of

simple feed forward networks the final activation values of an output layer are

immediately generated; in the case of feed back networks or recurrent ones the output

is generated in a more complex manner; yet in the end in all cases a certain output

vector is generated, i.e., each neuron of the output layer, if there is any, has obtained a

certain activation value. If there is no distinction between different layers as for

example it is the case with a Hopfield network or an interactive network the output

vector will consist of the final activation values of all neurons. Note that except in the

case of feed forward networks the output vector may be an attractor with a period p >

1. The network will then oscillate between different vectors, i.e. between different

states of the attractor. For theoretical and practical purposes neural networks are

mainly analyzed with respect to the input-output relation. Therefore, we define the

final state

of a neural network as S

= ((A

), (A

)), if (A

) is again the input vector

and (A

) the final output vector. If (A

) is an attractor with period p > 1, then the

components of (A

) consists of ordered sets, i.e. the set of all different activation

values the output neurons obtain in the attractor.

Because in the experiments described below we investigate only the behavior of

feed forward networks with respect to different MC-values, for practical purposes we

just define the final state as the values of the output vector after the external activation

via the input vector. Hence we speak of a large basin of attraction if many different

input vectors generate the same output vector and vice versa. The limiting case MC =

1 for example defines a network where each different input vector generates a

different output vector. Accordingly the case M = 1/n defines a network where

practically all n different input vectors generate the same output vector.

With these definitions it is easy to explain and measure in a formal manner the

characteristics of neural networks with respect to robustness. A robust network, i.e. a

network that is tolerant of faulty inputs, has necessarily a MC-value significantly

smaller than 1. Robustness means that different inputs, i.e. inputs that differ from the

correct one, still will generate the “correct” output, i.e. that output that is generated by

the correct input. That is possible only if some faulty inputs belong to the same basin

of attraction as the correct input; these and only these inputs from this basin of

attraction will generate the correct output. All other faulty inputs transcend the limits

of tolerance with respect to the correct output and will accordingly generate another

output. If MC = 1 or near 1 then the network will not be robust at all for the respective

reasons.

The same explanation can be given for the also frequently quoted capability of

neural networks to “generalize”: In a formal sense the generalizing capability is just

the same as robustness, only looked upon from another perspective. A new input can

be perceived as “similar” or as “nearly the same” as an input that the net has already

learned if and only if the similar input belongs to the same basin of attraction as the

input the network has been trained to remember. In other words, the training process

with respect to a certain vector automatically is also a training process with respect to

the elements of the according basin of attraction. The capability of generalization,

hence, can be understood as the result of the construction of a certain basin of

attraction. Accordingly the generalization capability is again dependent on the MC-

values: if these are small, i.e. if the basins of attraction are rather large, then the

network has a comparatively great generalizing capability and vice versa. Because

one network can have only one MC-value it is obvious that systems like the human

brain must have for one and the same perceiving task at least two different networks,

namely one with a great generalization capability, i.e., a small MC-value, and one

with a large MC-value to perceive different inputs as different.

Robustness and generalizing capability of a network, hence, can be “globally”

defined by the according MC-value. Yet there is a caveat: it is always possible to

generate networks via according training methods that are characterized by different

basins of attractions with different sizes. Therefore, the MC-value is not necessarily a

unique measure for the size of all basins of attraction of a particular network. The

term “basin of attraction” refers always only to a certain “equivalence class” of input

vectors, namely a set of input vectors that are equivalent in the sense that they

generate the same attractor. The size of these sets may be quite different for specific

attractors. Hence, the MC-value gives just an average measure with respect to the

different basins of attraction. With respect to some attractors and their generating

inputs the networks may be robust and with respect to others not. Considering that

possibility the concept of MC could also be defined as the difference in size of all

basins of attraction of the networks. Fortunately the results of our present experiments

hint at the fact that in most cases the basins of attraction of a certain networks differ

not much in size. The caveat is necessary for theoretical and methodical reasons but

seems not to be very important in practical contexts.

Concepts like “size of basins of attraction” and “values of meaning generation

capacity” obviously are very useful for the explanation of important characteristics

like robustness or generalizing capability. Yet in a strict sense they are too general

concepts because they only explain the behavior of certain neural networks from very

general characteristics of complex dynamical systems. They do not explain, which

structural characteristics of neural networks may be the reason for specific MC-

values. Hence, these concepts remain, so to speak, on a phenomenological level.

In the beginning of our article we mentioned the fact that frequently certain

topological characte-ristics of complex dynamical explain the behavior of such

systems. The topology of a neural network is mainly expressed in the weight matrix.

Hence the thought suggests itself to look for features of the weight matrix that could

explain the size of basins of attraction and MC-values. In anticipation of our results

we may say that we were successful in the sense that we found some general trends

although no deterministic relations.

2 Two Experimental Series

In the first experimental analysis we used a standard three-layered feed forward

network; we chose this type because it is very frequently used for tasks of pattern

recognition and related problems. Because, as is well known, two layers are not

enough to solve problems of non-linear separableness we took three layers in order to

get results for networks with sufficient efficiency. The input layer consists of 10 units,

the hidden layer of 5 and the output layer of 10 units. Input and output neurons are

binary coded, which results in 2

= 1024 possible input patterns. To keep the

experiments as clearly as possible we defined “equivalence classes” of input patterns:

all input patterns with the same number of zeroes are members of the same class. By

choosing at random one pattern from each class we obtained 11 different input

patterns. The activation function respectively is the sigmoid function; because of the

three layers we chose as learning rule the standard Back Propagation rule.

The training design was the following: In each step the network was trained to

associate different input patterns with one target pattern; the target pattern was again

chosen at random from the 11 input patterns. In the first step the tasks was to

associate each input pattern with one different target pattern; the according basins of

attraction all were of size one and the MC-value of this network after the training

process is 1:1. In the next steps the sizes of the basins of attraction were gradually

increased to 2, 3, 4, 5, and 6; in the last step the size of the only basin of attraction

finally was 11, i.e. all input layers had to be associated with one and the same target

pattern and the according MC-value is MC = 1/11. We did not investigate basins of

attraction with sizes 7 or 10 because in the according experiments the other basins

would become too small; for example, one basin of attraction with the size of 8 would

force the network to take into regard also at least one basin of attraction of size 3.

Hence we only investigated networks with basins of attraction of maximum size 5, 6,

and 11. By taking into regard different combinations of basins of attraction we

obtained 11 different networks.

The according weight matrices were analyzed with respect to the variance of their

weight values. This variance analysis was separately performed for the weight matrix

between the input layer and the hidden layer and the matrix between the hidden layer

and the output one. The results are shown in figure 1:

Fig. 1. Variance of the first part of matrix (left figure) and the second part (right figure) in

relation to the size of the basins of attraction.

The order of the different networks in both figures is according to increasing size

of the basins of attraction. No 1 is the case with MC = 1:1, no 11 is the network with

MC = 1:11.

The left figure obviously gives no unambiguous result with respect to possible

relations between variance values and the size of basins of attraction but it suggest a

certain trend, namely the decreasing of the variance by increasing the basins sizes.

The right figure confirms this and even shows an unambiguous result: The variance

values indeed gradually decrease with the increasing of the size of the basins of

attraction. We then combined the two matrices by summing up the variance values of

both matrices and obtained the final result shown in figure 2:

0 1 3 4 5 6 7 8 9 10 11 0 1 3 4 5 6 7 8 9 10 11

Fig. 2. Variance and size of basins of attraction for the whole network; the networks are

ordered as in figure 1.

This final result completely confirms the trend shown in figure 1, left side, and the

clear results of figure 1, right side: the larger the size of the basins of attraction are,

i.e., the smaller the MC-values are, the smaller are the variance values and vice versa.

By the way, the difference between the variance of the upper matrix and that of the

lower one is probably due to the fact that the Back Propagation rule does not operate

in exactly the same way on both matrices: The lower half of the whole matrix is

changed by directly taking into account the error, i.e. the distance between the output

neurons and those of the target vector. The changing of the upper half of the matrix is

done by computing a certain proportion of the error and thus “dispersing” the changed

weight values with respect to those of the lower half. Yet these just force the variance

of the whole matrix to the shown result. If our networks had contained only two

layers the whole result would have been like that of figure 2. We shall come back to

this effect of a certain learning rule in the next section.

We did not expect such unambiguous results yet on hindsight they are quite

plausible and comprehensible: Low variance values mean dispersion of information

or of the differences between different information respectively because of the near

equality of the weight values. If on the other hand the weight values are significantly

different, i.e. a high variance, then differences between different messages can be

preserved. As small or large sizes respectively of basins of attraction have exactly that

effect on the performing of messages it is no wonder that we obtained that clear and

unambiguous relation between variance and size of basins of attraction.

Yet although these clear results are quite satisfactory we knew very well that they

must be treated with a great methodical caveat: the behaviour of neural networks, as

that of practically all complex dynamical systems, depends on many parameters, in

this case for example on specific propagation, activation and output functions, number

of layers, special learning rules and so on. The results shown above were obtained

with a specific type of neural network, although a standard and frequently used one

with a standard learning rule. To make sure that our results are not only valid for this

special methodical procedure we undertook another experimental series.

In these experiments we did not use one of the standard learning rules for neural

networks but a Genetic Algorithm (GA). The combination of a GA with neural

networks has frequently been done since the systematic analysis of neural networks in

the eighties. Usually a GA or another evolutionary algorithm is used in addition to a

certain learning rule in order to improve structural aspects of a network that are not

changed by the learning rule, e.g. number of layers, number of neurons in a particular

layer, threshold values and so on. In our experiments we used the GA as a substitute

0 1 3 4 5 6 7 8 9 10 11

for a learning rule like the Back Propagation rule in the first experimental series. The

according weight matrices of the different networks are, when using a GA, written as

a vector and the GA operates on these vectors by the usual “genetic operators”, i.e.

mutation and recombination (crossover).

We chose this procedure for two reasons: On the one hand the operational logic of

a GA or any other evolutionary algorithm is very different from that of the standard

learning rules. A learning rule modifies usually just one network; in this sense it is a

simulation of ontogenetic learning. In contrast an evolutionary algorithm always

operates on a certain population of objects and optimizes the single objects by

selecting the best ones from this population at time t. This is a model of phylogenetic

evolution. In addition learning rules like the Back Propagation rule or its simpler

form, namely the Delta Rule, represent the type of supervised learning. Evolutionary

algorithms represent another type of learning, i.e. the enforcing learning. In contrast

to supervised learning enforcing learning systems get no feed back in form of

numerical values that represent the size of the error. The systems just get the

information if new results after an optimization step are better or worse than the old

ones or if there is no change at all in the improvement process. Therefore, the training

procedure in the second series is as different from that of the first one as one can

imagine.

We assumed that by choosing such different procedures similar results from both

experiments would be a very strong indicator for our working hypothesis, namely the

relation between MC-values or size of the basins of attraction respectively and the

mentioned characteristics of the according weight matrices. To be sure, that would not

be a final proof but at least a “circumstantial evidence” that the results of the first

series are no artifacts, i.e., that they are not only effects from the chosen procedure.

On the other hand we were in addition interested in the question if networks with

certain MC-values are better or worse suited to adapt to changing environmental

conditions. It is evident that per se high or low MC-values are not good or bad. It

always depends on the situation if a network performs better with high or low

capabilities to generate different meanings. Sometimes it is better to process a

message in a rather general fashion and sometimes it is necessary to perceive even

small differences. Yet from a perspective of evolutionary adaptation it is quite

sensible to ask if systems with higher or lower MC can adjust better. That is why we

used an evolutionary algorithm to investigate this problem although it is another

question than that of a relation between the variance of the weight matrix and the

according MC-values.

Because a GA can be constructed with using many different parameters like size of

the mutation rate, size of the sub vectors in crossover, selection schemas, schemas of

crossover (“wedding schemas”), keeping the best “parents” or not and so on it is

rather difficult to obtain results that are representative for all possible GA-versions.

We used a standard GA with a mutation rate of 10%, a population of 20 networks,

initially generated at random, crossover segments of 5, and a selection schema

according to the fitness of the respective networks. Because the networks were

optimized with respect to the same association tasks as in the first series those

networks are “fitter” than others that successfully have learned more association tasks

than others. If for example a network is optimized with respect to the task to operate

according to two basins of attraction of size 8 then a network is better that correctly

associates 6 vectors of each basin to the target vector than a network that does this

only for 5 vectors.

The population consists again of three-layered feed forward networks with binary

coding for input and output layers; the input and output vectors consist of four

neurons and the hidden layer of three. As in the first series the networks operate with

the sigmoid activation function. We simplified the networks a bit because, as

mentioned, a GA has not one network to operate with but a whole population. The

target vectors were chosen at random; the vectors for the respective basins of

attraction were chosen according to their Hamming distance to those output vectors

that define the basins of attraction. It is no surprise that the GA came faster to

satisfactory results, i.e. the generation of networks that are able to solve the respective

association tasks, if the MC-values of the networks should be large than in the cases

when the MC should be small. The main results are shown in figure 3:

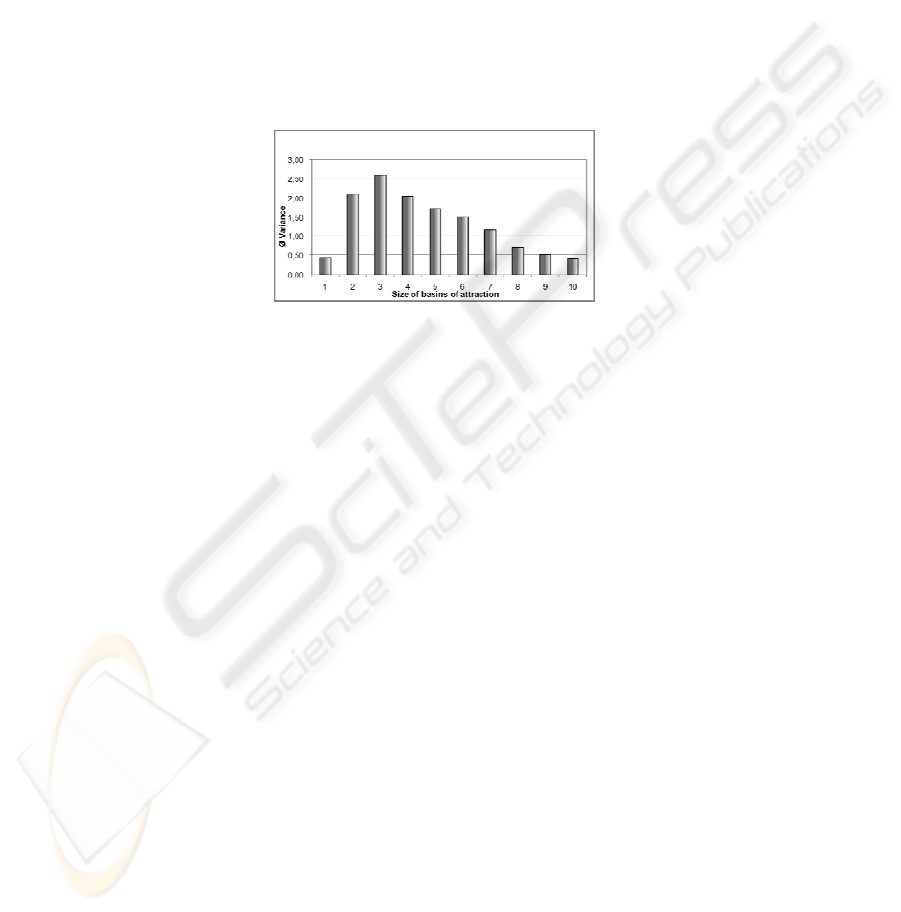
Fig. 3. Variance and size of basins of attraction in networks generated by a GA.

The figure obviously expresses a striking similarity to figure 1 of the first series.

The trend is the same, namely a clear relation between the size of the variance and the

increasing size of the basins of attraction or the decreasing size of the MC-values

respectively. Like in figure 1 the exceptions from this trend occur in the cases of

rather small basins of attraction, but only there. As we remarked in the preceding

section these exceptions may be due to the fact that the GA even more disperses the

weight values than does the Back Propagation rule for the upper half of the weight

matrix. This fact clearly demonstrates that the relation between variance values and

the sizes of the basins of attraction is “only” a statistical one, although the correlation

is very clear. We omit for the sake of brevity he results of the evolutionary analysis.

As we mentioned in the beginning of this section, the fact that such totally different

optimization algorithms like Back Propagation rule and GA, including the different

types of learning, generate the same trend with respect to our working hypothesis is

important evidence that the hypothesis may be valid in a general sense. Yet in both

series we just considered “case studies”, i.e. we concentrated in both cases on one

single network type and in the case of the GA-training on populations of the same

type of networks. That is why we started a third series.

3 Third Series: Statistical Analysis of Large Samples

Experiments with large samples of neural networks are always difficult because of the

large number of variables or parameters respectively that have to be taken into

account. Besides the influence of different learning rules, activation and propagation

functions and such parameters like learning rates and momentum the main problem is

a “combinatorial explosion”: if one takes into account the many different possible

combinations of neurons in the different layers and in addition the possible variations

of the number of layers one quickly gets such large samples that it is seldom possible

to obtain meaningful results. That is why we chose another way in the preceding

sections, namely the analysis of the two case studies in order to get a meaningful

hypothesis at all.

Yet despite the great difference between our two case studies it is always rather

problematic to draw general consequences from only several case studies. That is why

we studied a larger sample of two-layered neural nets, i.e., ca. 400.000 different

networks. We restricted the experiment to networks of two layers in order to keep the

experiments as clear as possible. The number of neurons in the input and output

vector are in all experiments the same and ranged from 3 to 10. The restriction to

equal dimensions of the two vectors was introduced because networks with different

sizes of the two vectors do not generate all MC-values with the same probability: If

the input vector is larger than the output one then MC = 1 would not be possible at all

because always more than one input vector will generate the same output vector. For

example, a simple network that is trained to learn a certain Boolean function has an

input vector of size 2 and an output vector of size 1. Its MC-value is 0.5. If conversely

the output vector is larger than the input vector the probability for large MC-values

will be greater than in networks with the same number of neurons in both vectors. To

avoid such distortions we used only vectors of equal size.

The networks were, as in the two case studies, binary coded and operated with the

sigmoid function. Thus we obtained ca. 400.000 pairs (MC, v), v being the variance.

The general results are the following:

As we supposed from the results of the two case studies the relation between

variance and MC-values is “only” a statistical one in the sense that there are always

exceptions from the general rule. Yet we discovered very clearly that indeed there is a

significant probability: the larger the variance is the smaller is the probability to

obtain networks with small MC-values, that is with large basins of attraction, and vice

versa. This result is in particular valid for variance values significantly large or small.

Only in the “middle regions” of variance values the probability to obtain MC-values

as a deviation from the general rule is a bit larger but not very much. This probability

distribution is shown in figure 4:

Fig. 4. Statistical relation between variance (x-axis) and MC-values (y-axis).

By the way, the deviations in the middle regions from the general trend may be a

first explanation for the mentioned results from section 2 with respect to the

1/n

evolutionary capability of networks with different MC-values. These networks adapt

more easily to changing environments than those with very large or very small values.

The hypothesis of the relation between MC-values and variance values seems to be

a valid one, at last as a statistical relation, Hence it is possible to predict the meaning

generating capacity of a network and thus its practical behaviour for certain purposes

with sufficient probability from a variance analysis of its weight matrix. Yet a caveat

is in order: We analyzed only one type of networks and further experiments are

necessary if our results are also valid for different types like, e.g. recurrent nets of

Self Organized Maps.

4 Interpretations and Conclusions

The behavior of complex dynamical systems can practically never be explained or

predicted by using only one numerical value (a scalar) as the decisive parameter. In a

mathematical sense the problem for such a system is always the task of solving

equations with a lot of variables, that is more variables than equations. It is well

known that for such tasks there is always more than one solution. When considering

neural networks by investigating the according weight matrix it is rather evident that

for example large basins of attraction may be constructed by very different matrices.

Hence, it is no wonder that the variance value, considered as a structural measure for

the occurrence of certain MC-values and the according sizes of the basins of

attraction, always allows for exceptions.

The knowledge about parameters that could predict the meaning generation

capacity would not only give important insights into the logic of neural network

operations; that would be an improvement of our theoretical understanding of these

complex dynamical systems. It could also give practical advantages if one needs

neural networks with certain capabilities – either if one needs robust networks with

great generalizing capacity or if there is need for sensitive networks that react in a

different manner to different inputs. To be sure, the relations we have discovered so

far are of only statistical validity. Yet to know that with a high probability one gets

the desired characteristics of a certain network if one constructs a weight matrix with

a specific variance is frequently a practical advantage: one has not to train the

networks and look afterwards if the network has the desired behavior but can

construct the desired matrix and if necessary make the additionally needed

improvements via learning rules and/or additional optimization algorithms like for

example a GA. For these theoretical and practical reasons it will be worthwhile to

investigate such relations as we have shown in this article further and deeper.

References

1. Klüver, J. and Klüver, C., 2007: On Communication. An Interdisciplinary and

Mathematical Approach. Dordrecht (NL): Springer.

2. Sacks, O., 1985: The Man Who Mistook His Wife for a Hat. New York: Summit Books.

3. Wolfram, S., 2001: A new Kind of Science. Champagne (Ill.): Wolfram Media.