A NEW IMAGE ENCRYPTION ALGORITHM USING CELLULAR

AUTOMATA

Mayank Varshney and D. RoyChowdhury

Indian Institute of Technology, Kharagpur, W.B. 721302, India

Keywords:

AES, Key scheduling, Cellular automata, Image encryption.

Abstract:

A signiﬁcant part of multimedia data to be transmitted over the network consists of image data. In this

paper,a cellular automata based image encryption algorithm which functions as a stream cipher has been

presented. This encryption algorithm is speciﬁcally intended towards encrypting the image data. Proposed

image encryption algorithm uses a hybrid cellular automata to produce a random key-stream while AES-key

expansion module infuses the reasonable security in the image encryption system.

1 INTRODUCTION

There exist several image encryption techniques be-

ing developed now a days such as SCAN-based meth-

ods (Bourbakis and Alexopoulos, 1992)(Alexopoulos

et al., 1995), CHAOS-based methods(Scharinger,

1998), permutation-combination based meth-

ods(Mitra et al., 2006) and cellular automata based

methods(Chen et al., 2006; Chen et al., 2005; Maleki

et al., 2008) etc. But, none of these image encryption

systems is suitable for transmission of image content

over a public communication network, as they are

too slow to work as online encryption which is

currently in demand. Online encryption requires a

image encryption system to be fast enough to so that

it can transmit the image data in real time and system

should be secure enough to prevent the third party

availing the image data content. The proposed image

encryption algorithm has been developed to fulﬁll

these requirements: speed and security. Proposed

image encryption/decryption method is based on xor

of image pixels with the corresponding pixels of the

Random Mask. Advance Encryption Standard is well

developed and tested standard in cryptography. Use

of s-box in key-scheduling function of AES makes

this image encryption method a non-linear function.

This non linearity of the image encryption algorithm

introduced by key-scheduling function provides rea-

sonable security of the encryption scheme. Whereas,

cellular automata has been used frequently in the ﬁeld

of cryptography as they are proved to produce pseudo

random pattern very efﬁciently. Proposed image

encryption algorithm utilizes a cellular automata and

a key-expansion function of AES for the purpose

of security and speed of the system. The proposed

image encryption system functions in decompressed

image domain i.e it encrypts only the decompressed

image content. To encrypt a compressed image

(JPEG/JBIG), compressed image must be decom-

pressed before the encryption (Dang and Chau, 2000;

Maniccam and Bourbakis, 2004; Wallace, 1999).

2 IMAGE ENCRYPTION

ALGORITHM

The proposed image encryption algorithm takes as in-

put 16-byte (128-bit) cipher key (CK)and encrypts a

m × n-pixel image, where ’m’ and ’n’ are variables.

The image encryption algorithm belongs to the class

of stream cipher and it produces blocks of key-stream

in the matrix format. These blocks are called as Ran-

dom Mask in this paper. The encryption algorithm

produces series of such random masks which are later

rearranged to produce a ﬁnal Random Mask for the

image. Each pixel of the image is xor-ed with the cor-

responding pixel of the Random Mask to produce an

encrypted image. A sketch of the image encryption

algorithm is drawn in ﬁgure 1. The 16-byte long ci-

pher key (CK) is given input to the Initial Permutation

function. The Initial Permutation function transforms

cipher key to produce 16 intermediate keys. Each of

these intermediate keys is called IK

(128-bit). The

secret intermediate key IK

is taken as initial state of

289

RoyChowdhury D. and Varshney M. (2009).

A NEW IMAGE ENCRYPTION ALGORITHM USING CELLULAR AUTOMATA.

In Proceedings of the International Conference on Security and Cryptography, pages 289-292

DOI: 10.5220/0002261902890292

 SciTePress

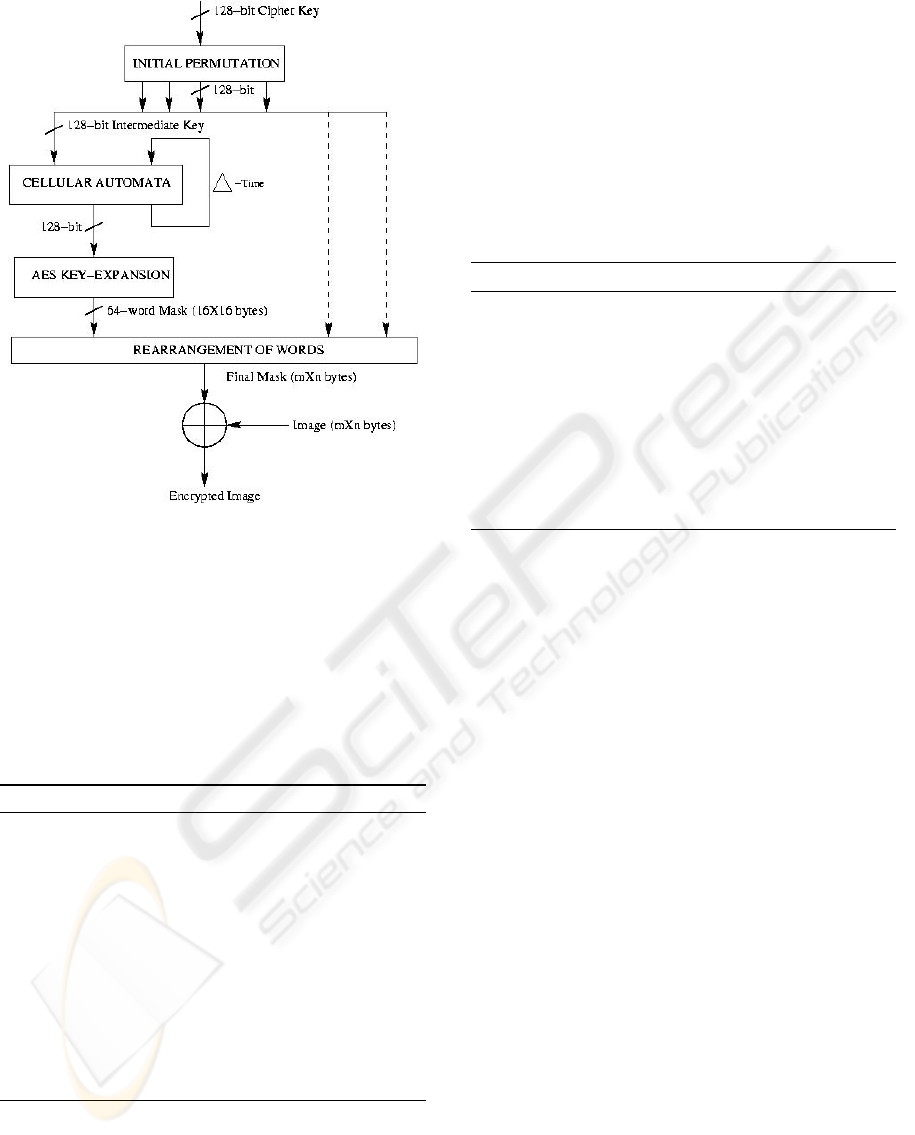
Figure 1: Outline of Encryption Algorithm.

the cellular automata. The cellular automata runs for

4 clock cycles and transforms intermediate key IK

(128-bit) into another intermediate key IK

(128-bit).

is given as input to the AES Key-Expansion func-

tion which expands IK

into a random mask RM

ake

(16 × 16 bytes). Each pixel (1-byte) of the image is

now bitwise xor-ed with the corresponding pixel (1-

byte) of Random Mask, called RM

f inal

after the rear-

rangement stage.

Algorithm 1. EncryptionAlgorithm(CK).

1: Input: m ×n image to be encrypted.

2: CK ⇐ CipherKey

3: Output: m ×n encrypted image.

4: IK

⇐ InitialPermutation(CK)

5: for all IK

6: IK

⇐ CellularAutomata(IK

)

7: for all IK

8: RM

ake

⇐ KeyExpansion(IK

)

9: RM

f inal

⇐ Rearrangement(RM

ake

)

10: end for

11: end for

12: E ⇐ I ⊕ RM

f inal

Initial Permutation linear function which itera-

tively applies one-byte-circular-left-shift on CK and

produces 16 byte long intermediate keys, called IK

This function outputs 16 such IK

’s, each of which

are given as input to the Cellular Automata. It has

been well researched that some conﬁgurations of rule

90 and rule 150 produces a pseudo random (reason-

ably random) pattern.(Chaudhuri et al., 1997; Serra

et al., 1990; Hortensius et al., 1989) Due to this propo-

erty, a cellular automata based key-stream generation

is adopted to speed up the process of Random Mask

generation. The CA runs for 4 number of clock

cycles producing more number of intermediate keys,

called IK

. Number of clock cycles, 4, linearly in-

creases with the size of the image to be encrypted.

A pseudo code for the cellular automata used in this

algorithm is given in Algorithm 2

Algorithm 2. CellularAutomata( IK

, IK

1: {Initializing Null-Boundary Conditions}

2: IK

[0] ⇐ 0

3: IK

[17] ⇐ 0

4: for i = 1 to 16 do

5: {Randomly choose between Rule 90 and Rule

150}

[i] ⇐ IK

[i −1] ⊕ IK

[i + 1]

[i] ⇐ IK

[i − 1] ⊕ IK

[i] ⊕ IK

[i + 1]

6: end for

Since, AES key expansion function uses the Sub-

stitution Box, key-expansion is an non linear func-

tion which process the IK

word by word, where one

word equal to four bytes. This function takes as input

4-word IK

and produces an array of 64 words RM

ake

(16X16 bytes). Four words of the IK

is copied into

ﬁrst 4 words of the expanded key, RM

ake

. The remain-

der of the RM

ake

is ﬁlled four words at a time. Each

added word w[i] depends on the immediately preced-

ing word w[i-1], and the word 4 position back, w[i-4].

In three of four cases, a simple xor of w[i-1] and w[i-

4] is used, but for a word whose position in the word

array is multiple of 4, a more complex function ”g” is

used.

3 SECURITY OF THE IMAGE

ENCRYPTION ALGORITHM

The Cellular Automata module of the image encryp-

tion algorithm uses a 128-bit linear cellular automata

with a conﬁguration of rule 90 and rule 150. It has

been well studied that maximum length group cellular

automata generates a very good random pattern (Bao,

2004). For a 128-bit linear cellular automata with two

possible rules at each cell,the order of possible solu-

tion for this CA is 2

128

. Hence, if rule 90 and rule 150

are applied randomly at each cell, cryptanalysis of this

CA will require computation of order 2

128

. Since, this

image encryption algorithm supports variant key sizes

SECRYPT 2009 - International Conference on Security and Cryptography

290

of 128, 192 and 256 bits, the cryptanalysis of higher

key size CA will require computational power of or-

der > 2

128

3.1 Security Against Statistical Attacks

A histogram of the original image shows a biased pat-

tern of pixel values i.e. some values are more likely

to happen than other pixel values,because of correla-

tion among the pixels of the image. This property is

quite visible in the histogram shown in the Figure 2.

Histogram of the Random Mask generated by image

encryption algorithm, depicts that all pixel values are

evenly distributed and the same property is forwarded

into the encrypted image when original image is xor-

ed with the Random Mask. Histogram of the en-

crypted image shows an evenly distributed pattern of

pixel values which makes it more robust towards any

statistical/correlation attack.

(a) Image (b) (c) Mask (d)

(e) After En-

cryption

(f) (g) After

Decryption

(h)

Figure 2: Histogram Analysis.

3.2 Randomness of the Computed Mask

Randomness is a probabilistic property i.e the prop-

erties of a random sequence can be characterized and

described in terms of probability. There are 16 differ-

ent test recommended by NIST (National Institute of

Standards and Technology) so that statistical testing

may be interpreted reasonably with out drawing any

incorrect conclusions (NIST, )(NIST, 2001). For any

statistical test, if the computed P-value is < 0.01, then

it is concluded that the sequence is non-random. Oth-

erwise, it is concluded that the sequence is random.

Following are the used parameters for different tests.

1. Monobit Frequency Test

(a) Number of Sequences/Samples = 100

(b) Sequence Length = 10

bits

2. Frequency Test within Block

(a) Number of Sequences/Samples = 100

(b) Sequence Length = 10

bits

3. Longest Run of Ones Test

(a) Number of Sequences/Samples = 20

(b) Sequence Length = 75 × 10

bits

4. Linear Complexity Test

(a) Number of Sequences/Samples = 30

(b) Sequence Length = 75 × 10

bits

(a) Frequency

Test

(b) Frequency

Test With in

Block

of Ones Test

(d) Linear Com-

plexity Test

Figure 3: Plot of P-values for Different Tests.

3.3 Confusion and Diffusion Properties

of Encryption Algorithm

At ﬁrst, decryption has been done with the correct ci-

pher key and secondly, decryption has been done with

an incorrect cipher key which differs from correct ci-

pher key by only one bit. The decrypted image with

the incorrect cipher key shows a random image even

though the cipher key has been changed only by one

bit.

In order to show the confusion property of the

image encryption algorithm, two chosen image have

been encrypted with the same cipher key and the re-

spective histogram have been shown in Figure 4.

4 CONCLUSIONS

This image encryption scheme can lead to very efﬁ-

cient software as well as hardware implementation.

Results from statistical tests indicate that Random

Mask generated bythe image encryption algorithm is

reasonably random to defy the distinguishing attack

and any statistical test as well. However, more test-

ing and cryptanalysis efforts are required to precisely

assess the efﬁciency and security of the algorithm.

A NEW IMAGE ENCRYPTION ALGORITHM USING CELLULAR AUTOMATA

291

(a) Original

Image

(b) De-

crypted

Image with

Incorrect

Key

crypted

Image with

Correct Key

(d) Bird Im-

age

(e) Plain Im-

age

(f) En-

crypted Bird

Image

(g) En-

crypted Plain

Image

(h) His-

togram of

Bird Image

(i) His-

togram of

Plain Image

(j) His-

togram of

Encrypted

Bird Image

(k) His-

togram of

Encrypted

Plain Image

Figure 4: Different Images and their Histograms showing

the Confusion Property.

REFERENCES

Alexopoulos, C., Bourbakis, N., and Ioannou, N. (1995).

Image encryption method using a class of fractals.

Electronic Imaging, (4):251–259.

Bao, F. (2004). Cryptanalysis of a partially known cellular

automata cryptosystem. IEEE TRANSACTIONS ON

COMPUTERS, 53(11):1493–1497.

Bourbakis, N. and Alexopoulos, C. (1992). Picture data

encryption using scan patterns. Pattern Recognition,

25(6):567–581.

Chaudhuri, P. P., RoyChowdhury, D., Nandi, S., and Chat-

topadhayay, S. (1997). Additive Cellular Automata -

Theory and Its Application, volume 1, chapter 4. IEEE

Computer Society Press.

Chen, R.-J., Chen, Y.-H., Chen, C.-S., and Lai, J.-L. (2006).

Image encryption/decryption system using 2-d cellu-

lar automata. IEEE Tenth International Symposium on

Consumer Electronics (ISCE).

Chen, R.-J., Lu, W.-K., and Lai, J.-L. (2005). Image encryp-

tion using progressive cellular automata substitution

and scan. IEEE International Symposium on Circuits

and Systems, 2:1690–1693.

Dang, P. P. and Chau, P. M. (2000). Image encryption for

secure internet multimedia applications. IEEE Trans.

Consumer Electronics, 46:395–403.

Hortensius, P. D., Card, H. C., and McLeod, R. D. (1989).

Parallel random number generation for vlsi using cel-

lular automata. IEEE Trans. Comput., 38:1466–1473.

Maleki, F., Mohades, A., Hashemi, S. M., and Shiri, M. E.

(2008). An image encryption system by cellular au-

tomata with memory. Third International Conference

on Availability, Reliablitiy and Security, pages 1266–

1271.

Maniccam, S. S. and Bourbakis, N. G. (2004). Image and

video encryption using scan patterns. Pattern Recog-

nition 37, pages 725–737.

Mitra, A., Rao, Y. V. S., and Prasanna, S. R. M. (2006).

A new image encryption approach using combina-

tional permutation techniques. International Journal

of Computer Science, 1(2).

NIST. Random number generation. website.

http://csrc.nist.gov/groups/ST/toolkit/rng/index.html.

NIST (2001). A statistical test suit for ran-

dom and pseudorandom number genera-

tors for cryptographic applications. website.

http://csrc.nist.gov/groups/ST/toolkit/rng/documents/

SP800-22b.pdf.

Scharinger, J. (1998). Fast encryption of image data us-

ing chaotic kolmogorov ﬂows. Electronic Imaging,

17(2):318–325.

Serra, M., Slater, T., Muzio, J. C., and Miller, D. M. (1990).

The analysis of one-dimensional linear cellular au-

tomata and their aliasing properties. IEEE Transac-

tions on Computer-aided Design, 9(7).

Wallace, G. K. (1999). The jpeg still picture compression

standard. IEEE Transactions on Consumer Electron-

ics.

SECRYPT 2009 - International Conference on Security and Cryptography

292