An Adaptive Cruise Control System based

on Self-Learning Algorithm for Driver Characteristics

Lei Zhang, Jianqiang Wang and Keqiang Li

State Key Laboratory of Automotive Safety and Energy

Tsinghua University, Beijing 100084, China

Abstract. An Adaptive Cruise Control system prototype based on self-learning

algorithm for driver characteristics is presented. To imitate the driver opera-

tions during car-following, a driver model is developed to generate the desired

throttle depression and braking pressure. A self-learning algorithm for driver

characteristics is proposed based on the Recursive Least Square method with

forgetting factor. Using this algorithm, the parameters of the driver model are

real-time identified from the data sequences collected during the driver manual

operation state, and the identification result is applied during the system auto-

matic control state. The system is verified in a driving assistance system test-

bed with electronic throttle and electro-hydraulic brake actuators. The experi-

mental results show that the self-learning algorithm is effective and the system

performance is adaptive to driver characteristics.

1 Introduction

With the traffic density increasing rapidly, car-following has become the most fre-

quent driving scenario to the driver. In the vehicle active safety field, several types of

driving assistance systems have been actualized for the car-following scenario such as

Adaptive Cruise Control (ACC) [1], Stop & Go (S&G) [2] and Forward Collision

Warning/Avoidance (FCW/FCA) [3]. The aims of the systems are to facilitate driver

to maintain a safe and comfortable car-following state or to mitigate the workload of

the driver [4]. Because of the interaction between the driver and the assistance sys-

tem, the driver behavior and characteristics during car-following have been consi-

dered as important issues in system development.

The research on modeling driver behavior in car-following scenario dates back to the

1950s and many types of models were established with different approaches [5]. The

classical method is using mathematic functions to represent the relationship between

variables like host vehicle speed, acceleration, relative speed and distance headway,

such as the Gazis-Herman-Rothery (GHR) model [6], the Gipps model [7] and the

linear (Helly) model [8]. These models can be applied to the system control algo-

rithm, but as the required outputs of the models are the desired vehicle motion states,

complicated vehicle dynamics model needs to be added. Some models are designed to

imitate the driver’s throttle and braking operations directly [9]. This method could

avoid the vehicle dynamics problem such as the inverse model of vehicle longitudinal

Zhang L., Wang J. and Li K. (2009).

An Adaptive Cruise Control System based on Self-Learning Algorithm for Driver Characteristics.

In Proceedings of the 3rd International Workshop on Intelligent Vehicle Controls & Intelligent Transportation Systems, pages 17-26

 SciTePress

dynamics. However, the parameters of these models are fixed during system opera-

tion and cannot be adaptive to individual driver car-following characteristics.

In this paper, a driver model is proposed to imitate throttle and braking operations of

the driver and a self-learning algorithm for driver characteristics is designed based on

Recursive Least Square (RLS) method with forgetting factor. Using this algorithm,

the parameters of the driver model can be real-time identified from the data sequences

collected during manual driving operation state, and the identification result is applied

during the system automatic control state. The driver model and the self-learning

algorithm are implemented in a driving assistance system test-bed and the functions

of the system are validated by tests in real traffic.

2 Driver Behavior Test and Characteristics Analysis

The driver behavior during car-following is a significant factor for the development

of driving assistance system. To investigate essential driver characteristics and estab-

lish driver behavior database, driver behavior tests in real traffic environment are

executed and the signals including host vehicle speed, acceleration, depression of

accelerator pedal/throttle, braking pressure, relative distance/speed to leading vehicle,

and GPS information are recorded with 10Hz data capture frequency. Thirty drivers

are invited as experimental subjects to drive on the city highway for 1 hour per per-

son. The drivers are suggested to drive freely according to their own styles and habits.

The data sequences of steady car-following behavior, which corresponds to the ACC

function, are extracted from the test data. This behavior is defined as that the driver

controls the host vehicle to follow a constant leading vehicle steadily more than 15

seconds without braking and lane-changing. Two common variables are discussed in

the data analysis to describe driver characteristics. One is Time Headway (THW):

THW

(1)

The other one is Time-to-Collision (TTC, and its inverse TTCi):

TTC TTCi

(2)

Where: D is the distance between the host vehicle and the leading vehicle; v is the

host speed vehicle; and v

is the host vehicle’s relative speed to the leading vehicle.

The frequency contour of THW and TTCi of one driver’s steady car-following beha-

vior is shown in Fig 1. The number on each area border (50%, 75%, 95% and 99%)

in this figure means the percentage of the data points falling inside this border. It is

clear that 50% of THW and TTCi data distribute in a relatively concentrated area

where THW is around 1.2s to 2.6s and TTCi is around -0.05 to 0.05s

-1

. This pheno-

menon indicates that the driver prefers to keep THW and TTCi in specific ranges, and

these two variables can be considered as the driver control targets during car-

following for the driver model design.

this analysis, a driver model is proposed:

() () [ () ] ()

des ss THW d TTCi

p t Th t K THW t THW C TTCi t=+⋅ −+⋅

(3)

Where: P

des

(t) is generalized depression at time t; Th

(t) is steady throttle depression

to keep the current host vehicle speed v(t); THW

is the driver’s desired time headway;

THW

and C

TTCi

are error gains of THW and TTCi respectively.

Interpolation method is used for Th

calculation based on the experimental calibra-

tion. The desired control variables, Th

des

and Pb

des

, are calculated according to the

value of the generalized depression p

des

. The throttle depression for idle-speed is 15.

When p

des

(t) >15:

() ()

() 0

des des

des

Th t p t

Pb t

⎧

⎨

⎩

(4)

Considering the driver’s operation delay at the switching between accelerator and

brake pedal, the braking control is not activated immediately when p

des

(t) falls below

the idle-speed depression 15. When 15>= p

des

(t) >10:

() 15

() 0

des

Th t

Pb t

⎧

⎨

⎩

(5)

When p

des

(t) <=10:

() 15

() [ () 10]

des

des pb des

Th t

Pb t B p t

⎧

⎪

⎨

=⋅ −

⎪

⎩

(6)

Where: B

is the gain from p

des

to Pb

des

, whose value is set as -0.1, and the unit of the

desired brake pressure Pb

des

is MPa. The maximal value of Pb

des

is set as 10MPa.

4 Self -Learning Algorithm for Driver Characteristics

The driver model could describe the driver characteristics and present the individual

differences during car-following. The parameter THW

presents the driver’s preferred

following distance at same vehicle speed level and reflect his/her aggressive degree.

The parameters K

THW

and C

TTCi

present the driver’s sensitivity of THW error and TTCi

error. To improve the system’s adaptability of individual driver characteristics, a self-

learning algorithm based on Recursive Least Square (RLS) method is proposed. The

core idea of this algorithm is to identify the model parameters from the driver manual

car-following drive state on-line and apply the identification result to the model dur-

ing system automatic driver state. Because of the time-variability of the driver, it is

supposed that the latest data of driver operation will describe the driver characteristics

more accurately and therefore, forgetting factor is brought into the algorithm. The

flow chart of this self-learning algorithm is shown in Fig 3.

Fig. 3. The flow chart of self-learning algorithm.

After the system initialization, the signal collection of distance D, relative speed v

host vehicle speed v and throttle depression Th is enabled. The driver selects the drive

states. During the driver manual control process, the algorithm starts the cycle to

judge the car-following state and identify the parameters step-by-step. The system

step length is 0.1s. The parameters THW

, K

THW

and C

TTCi

are identified from steady

car-following data sequence.

The first condition is that the leading vehicle should be a constant target (i.e. no target

changing such as cut-in and cut-out scenarios) and this condition is judged according

to the variation of the distance signal. Furthermore, the driver is not controlling the

brake system. At step k:

() ( 1) 5

() 0

DDk Dk

⎧Δ = − − <

⎪

⎨

⎪

⎩

(7)

If the first condition is satisfied, the algorithm will use the current data D(k), v

(k), v(k)

and Th(k) to start the iteration process of LRS method.

The observation vector of the iteration process is h

(k):

Where:

() ( 1)

()

THW

THW k THW k

THW k

−

Δ=

(14)

() ( 1)

()

THW THW

THW

KkKk

−

Δ=

(15)

() ( 1)

()

TTCi TTCi

TTCi

CkCk

−

Δ=

(16)

is the threshold, which is 0.5% in this algorithm.

Because that the driver state is time-varied, the identified parameters are always fluc-

tuating. In order to find the parameters describing the driver characteristics as precise-

ly as possible, an accumulation method is used:

()

sum sum t

k=+PPP

(17)

All parameters satisfied the conditions are accumulated to P

sum

and when the drive

state switches to system automatic driving, the current parameter vector P

is called

by the driver model:

(18)

Where: N is the counter of the parameters.

With the running time increasing, the algorithm will accumulate more identified re-

sults from driver manual operation and the learning effect will be improved. The

driver model will be closer to the driver average characteristics. During the algorithm

running process, if any of the three conditions are not satisfied, the iteration will be

stopped and the current P

sum

and N will be held. Until new proper parameters are

identified, the accumulation will be continued.

5 System Verification in Driving Assistance System Test-bed

A test-bed on a passenger car is developed to verify the system functions including

driver characteristics self-learning algorithm and ACC. During the self-learning algo-

rithm verification experiment, a driver subject drives the test-bed vehicle in real traf-

fic and the self-learning algorithm runs online synchronously to identify the model

parameters. The parameter identification test continues for 600 seconds to make the

results closer to the driver average characteristics, Fig 4 gives the driver manual oper-

ation data sequence when following a specified leading vehicle. Fig 5 shows the pa-

rameter identification process from this data sequence. It is indicated that the algo-

rithm is effective and the parameters tend to be stable gradually after some fluctuation

at the beginning. At the end of the test, the final identification results are: THW

1.84, K

THW

= 33.5, C

TTCi

= -109.5.

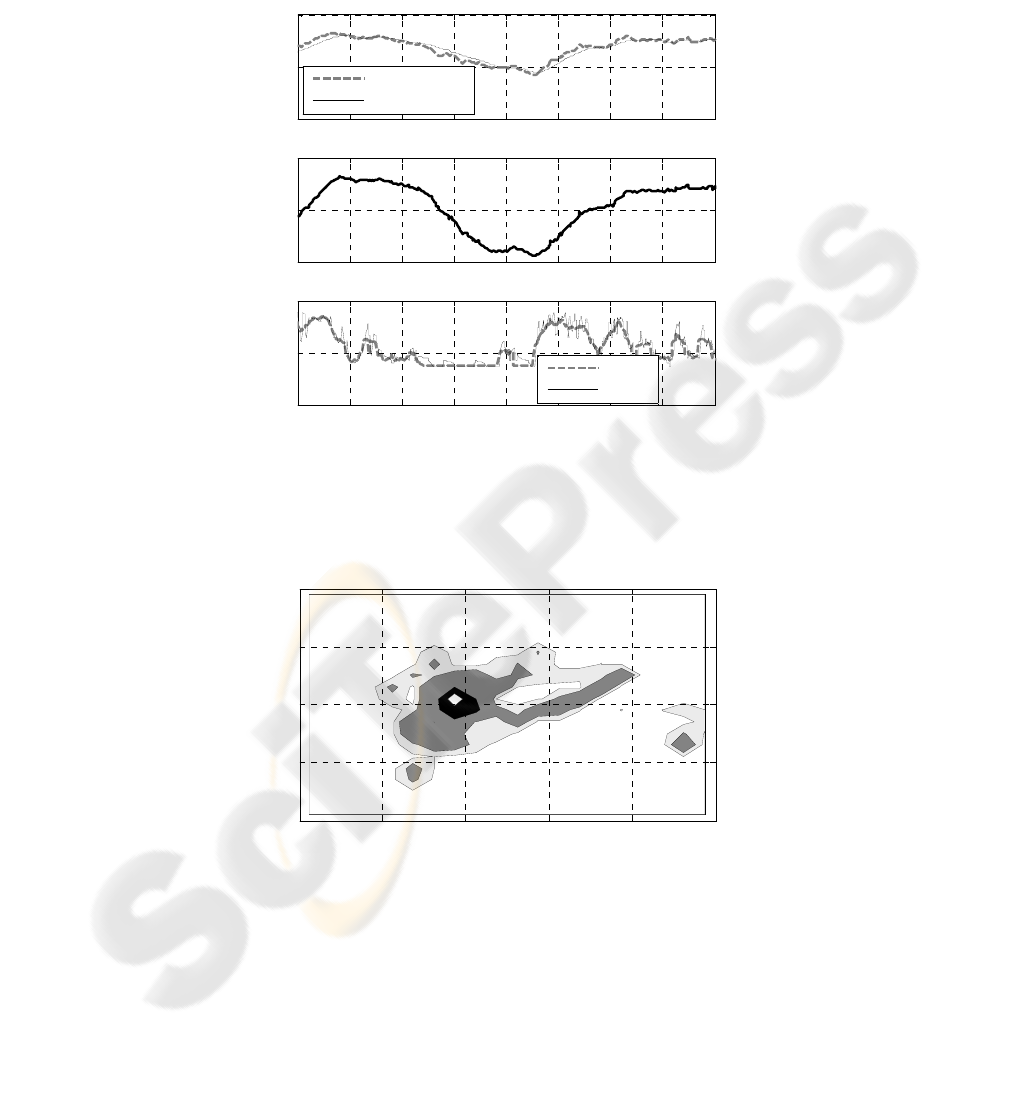
Using these identified parameters, the system is switched to ACC mode and Fig 6

shows a data sequence of system automatic car-following. The system can track the

leading vehicle’s speed steadily and keep safety distance. The control performances

of the upper and lower controllers are both favorable.

25 30 35 40 45 50 55 60 65

Speed (m/s)

Leading Vehicle

Host Vehicle

25 30 35 40 45 50 55 60 65

Distance (m)

25 30 35 40 45 50 55 60 65

Throttle (%)

Time (s )

Des ir ed

Actual

Fig. 6. The performance of the system ACC function.

More experiments of ACC verification are carried out in real traffic and the system

performance is analyzed with THW-TTCi frequency contour, which is shown in Fig 7.

THW (s )

TTCi (s

-1

)

0 1 2 3 4 5

-0.2

-0.1

0.1

0.2

Fig. 7. Frequency contour of THW and TTCi during system control.

Comparing with Fig.1, it is indicated that the overall data distributions (99% percen-

tage) of the system and the driver are similar. Based on the parameter identified from

the driver behavior, the system performance is adaptive to the driver characteristics

and gives the driver comfortable riding experience. Furthermore, the 50% and 75%

areas of system performance are more centralized than the driver. This result indicates

that the THW and TTCi fluctuations during system control state are much smaller and

the system is more stable than the driver.

6 Conclusions

In this paper, an Adaptive Cruise Control system prototype with self-learning func-

tions is developed on a passenger car test-bed.

(1) Driver real traffic tests are carried out and the driver behavior database for the

system upper controller design is established. The data analysis of steady car-

following show that the driver prefers to keep THW and TTCi in specific ranges, and

a driver model is designed based on this result.

(2) The Recursive Least Square method with forgetting factor can identify the driver

model parameters online from data sequence of driver manual operation state, and the

self-learning algorithm for driver characteristics is proposed with this method.

(3) The experimental results show that the ACC system can be adaptive to the driver

characteristics automatically with the learned parameters. The system has similar

performance with the driver manual operation and favorable acceptability of driver.

References

1. Ohno, H.: Analysis and modeling of human driving behaviors using adaptive cruise control.

Industrial Electronics Society, IECON 2000, 26th Annual Conference of the IEEE, Vol.4,

2803-2808 (2000)

2. Yi, K., Hong, J., Kwon, Y. D.: A Vehicle Control Algorithm for Stop-and-Go Cruise Con-

trol. Proceedings of the Institution of Mechanical Engineers. Part D, Journal of automobile

engineering, Vol. 215, 1099-1115 (2001)

3. Lemaire, E., El Koursi, E.M., Deloof, P., Ghys, J. P.: Safety Analysis of a Frontal Collision

Warning System. IEEE Intelligent Vehicles Symposium, Vol. 2, 453 – 458 (2002)

4. Yoshida, T., Kuroda, H., Nishigaito, T.: Adaptive Driver-assistance Systems. HITACHI

Review (2004)

5. Mark Brackstone, Mike McDonald: Car-Following: A Historical Review. Transportation

Research Part F, Vol. 2: 181~196 (1999)

6. Gazis, D. C., Herman, R., & Rothery, R. W.: Nonlinear follow the leader models of traffic

flow, Operations Research, Vol. 9, 545-567 (1961)

7. Gipps, P. G.: A Behavioral Car Following Model for Computer Simulation. Transportation

Research B, Vol.15: 105-111 (1981)

8. Helly, W.: Simulation of Bottlenecks in Single Lane Traffic Flow. In Proceedings of the

Symposium on Theory of Traffic Flow, Research Laboratories, General Motors, 207-238

(1961)

9. Erwin R. B., Nicholas J. W., Michael, P. M., Nobuyuki K.: Driver-Model-Based Assess-

ment of Behavioral Adaptation. Proceedings. JSAE Annual Congress (2005)

10. Enso Ikonen, Kaddour Najim Advanced Process Identification and Control, CRC Press,

2002, ISBN 082470648X