
A COMBINATION OF CONNECTIONIST SYSTEMS AND
EVOLUTIONARY COMPUTATION TECHNIQUES TO ACHIEVE
THE OPTIMAL DOMAIN FOR STELLAR SPECTRA SIGNAL
PROCESSING
Diego Ord´o˜nez, Carlos Dafonte, Bernardino Arcay
Department of Information and Communications Technologies, University of A Coru˜na, 15071, A Coru˜na, Spain
Minia Manteiga
Department of Navigation and Earth Sciences, University of A Coru˜na, 15071, A Coru˜na, Spain
Keywords:
Genetic algorithm, Artificial neural network, Connectionist systems, FFT, Wavelet transform, GAIA mission,
Stellar spectra, Stellar parameters.
Abstract:
This paper presents part of the work carried out by Coordination Unit 8 of the GAIA project. GAIA is
ESA’s spacecraft which is planned to be operative at the start of 2012 and will carry out an a stereoscopic
census of the Galaxy. During the present development cycle, synthetic spectra are used to determine the
stellar atmospheric parameters, particularly effective temperatures, superficial gravities, metallicities, possible
abundances of alpha elements, and individual abundancies of certain chemical elements. We present the results
of the application of genetic algorithms to the selection of relevant information from a set of spectra. This
information will subsequently feed an artificial neural network that is in charge of extracting the parameters.
1 INTRODUCTION
Spectral parameterization, the process of ascertain-
ing a star’s main physical properties (effective tem-
perature and gravity, atmospheric metal content, ro-
tation, etc.) from a stellar spectrum, is a well-
known problem in astrophysics. Many previous stud-
ies have been devoted to the search for an efficient
algorithm to perform automated parameterization in
extensive spectral archives or astronomical spectral
datasets ((Bailer-Jones, 2008), (Kaempf et al., 2005),
(Bailer-Jones, 2000), (Hippel et al., 2002)). A first
approach may be obtained through the use of the clas-
sical Morgan-Keenan (MK) classification system for
stellar spectra (Morgan W.W., 1943). The MK sys-
tem is based on the direct comparison of stellar spec-
trum features with those of the set of MK standards
that define stellar types and luminosity classes, with
these two classification stages directly related to stel-
lar temperature and stellar gravity. The advantage
of this approach is that it functions well, even with
low-resolution spectra, and that it does not depend
on atmospheric models of the stars. However, this
traditional classification method depends to a great
extent on the expertise of the spectroscopist, and it
is slow and subjective. This is why an automatic
and robust method has become an essential require-
ment in the analysis of large datasets, both for the ho-
mogeneity of the results and the repeatability of the
process. The currently existing (and planned) astro-
nomical data archives have also triggered this inter-
est for automatic classifiers. Modern telescopes are
equipped with spectrometers that are able to observe
a large number of objects per frame. The current and
future astronomical databases of ground telescopes
and spatial missions, such as the Sloan Sky Survey or
the GAIA mission, will gather large amounts of spec-
tra that belong to various components of our galaxy.
The ESA’s Gaia spacecraft is planned to be operative
at the beginning of 2012. Its purpose is to perform a
stereoscopic census of the Galaxy, measuring astrom-
etry for approximately 10
9
astronomical sources (De-
partment, ) with unprecedented precision. The mis-
sion will also study the astrophysical nature of the
sources, by direct classification among principal as-
tronomical classes (stars, physical binary stars, non-
physical binaries, galaxies, quasars, and minor plan-
ets). In the case of the brightest sources, up to magni-
323
Ordóñez D., Dafonte C., Arcay B. and Manteiga M. (2009).
A COMBINATION OF CONNECTIONIST SYSTEMS AND EVOLUTIONARY COMPUTATION TECHNIQUES TO ACHIEVE THE OPTIMAL DOMAIN
FOR STELLAR SPECTRA SIGNAL PROCESSING.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 323-330
DOI: 10.5220/0002264403230330
Copyright
c
SciTePress
tude 17 (mainly stars), a parameterization of the main
properties will be performed.
Our research group is a member of GAIA’s sci-
entific team, which was created to prepare the opti-
mal algorithms that will allows us to carry out clas-
sification and parameterization tasks. The main ob-
jective is to determine the stellar atmospheric param-
eters, particularly effective temperatures, superficial
gravities, metallicities, possible abundances of alpha
elements, and individual abundances of certain chem-
ical elements. The manipulation, analysis, and classi-
fication of all the information concerning the visible
celestial bodies up to magnitudes 17− 18 is undoubt-
edly a challenge for both Astrophysicists and Com-
puter and Artificial Intelligence Scientists.
A volume of data of this magnitude can only be
managed and mined using automatic methods. His-
torically, the techniques that have most often been ap-
plied to automatic spectra parameterization are artifi-
cial neural networks and minimal distance methods.
Neural networks are especially interesting, as they
have a high noise tolerance ((Ordonez et al., 2008)),
and the spectra in general will be presented to the net-
work with different degrees of noise, as we may see
in section 3. We have previously referred to a number
of studies intended to determine the physical parame-
ters of stellar spectra through the use of artificial neu-
ral networks (ANN) and synthetic data sets (Harinder
et al., 1998), (Bailer-Jones, 2000) and (Hippel et al.,
2002); and the more recent ones by (Fiorentin et al.,
2007) and (Bailer-Jones, 2008).
Genetic algorithms have been used in combina-
tion with artificial neural networks, with great suc-
cess in many cases ((Hu, 2008), (Rooij et al., 1996),
(Kinnebrock, 1994)). In this study we combined both
techniques in order to achieve an efficient solution to
the problem of spectra parameterization. In contrast
to the previously mentioned studies (the optimiza-
tion of network parameters), the genetic algorithm in
question was used to optimise input to the network
(the selection of relevant characteristics of the input
data). This work presents our first results on the auto-
matic parameterization of atmospheric stellar param-
eters (RVS spectral region) using ANNs trained with
synthetic stellar spectra and input optimized with ge-
netic algorithms.
2 SIGNAL PROCESSING
TECHNIQUES
The automatic techniques for classifying and param-
eterizing spectra are normally used in combination
with some means of processing the signal prior to
analysis. This process may have different goals:
from reducing the dimensionality of the original sig-
nal (number of points), to a transformation required
to explain certain features that were concealed in its
original format.
The first transformation applied in this study is
the discrete Wavelet transform. An efficient way of
applying this transformation using filters was devel-
oped in 1988 by Mallat (Mallat, 1989). This fil-
tering algorithm produces a fast Wavelet transform.
We will refer to this process as a multilevel analy-
sis, which in this case we will apply to spectra. In
the wavelet analysis reference is made to approxima-
tions (low frequency components) and details (high
frequency components). The concept of multilevel
analysis refers to the repeated application of the filter-
ing process to each of the successive approximations
obtained in the signal, achieving a new level after each
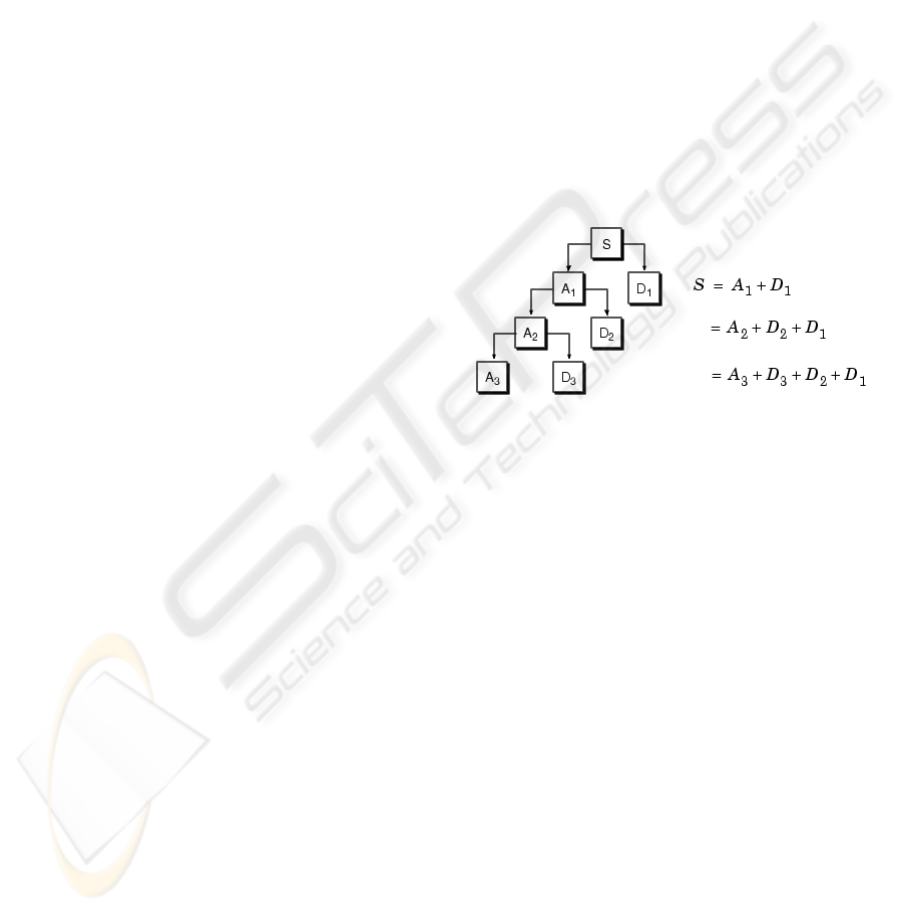
of these stages (Figure 1).
Figure 1: Discrete Wavelet Transform. Multilevel decom-
position.
The experiment considers a total of three filtering
levels, as shown in Figure 1. Three levels were cho-
sen because as we descend to each level, the number
of points for approximations and details is reduced by
roughly half, and the approximations for lower lev-
els signify very few points. In this Figure we may
also see that by applying the approximation and detail
for a level, it is possible to obtain the approximation
of the previous level by applying the inverse wavelet
transform. This means that in order to carry out the
experiment it is not necessary to consider all of the
signals from the tree decomposition provided by the
transform. Instead, we take the approximation from
the lowest level and all of the details. By adding the
number of points from all of these signals, we obtain a
similar value to the number of points from the original
signal.
Another of the pre-processing techniques fre-
quently used for transforming stellar spectra is Prin-
cipal Component Analysis, or PCA. The advantage
of using this technique is that it reduces the dimen-
sionality of the input data by eliminating variables
with little information. It is used to determine the
number of explanatory underlying factors of a series
IJCCI 2009 - International Joint Conference on Computational Intelligence
324

of data that explain its variability. Previous studies
((Harinder et al., 1998)) have obtained worse results
in analysing stellar spectra by applying PCA than by
applying methods based on Wavelets ((Ordonez et al.,
2008)).
PCA is an input-oriented analysis, meaning that
it does not take into account the results we wish to
obtain from the input (specific parameter). It also
requires the involvement of an expert to decide how
much typical deviation of the input data is represented
in the selected variables once processing has been car-
ried out. We aimed to predict four parameters based
on a spectrum (temperature, gravity, metallicity and
abundance of light elements), in the hope that the rel-
evant points from the spectrum to ensure correct pa-
rameterization are different, depending on the case.
For this reason we had to find a method that made
it possible to reduce the dimensionality of the signal
oriented to the parameter we wished to predict. The
technique we chose in order to achieve these objec-
tives was to use genetic algorithms. This technique
will provide us with a selection of the relevant and
specific points of the signal for each of the parame-
ters we aim to obtain.
Also, considering the good results obtained based
on the wavelet analysis applied to spectra (Ordonez
et al., 2008), instead of applying the genetic algorithm
technique directly on the signal, we have applied it to
the result of applying the wavelet transform as previ-
ously described.
3 DATA DESCRIPTION
For our tests the Gaia RVS Spectralib was used, a li-
brary of stellar spectra compiled by A. Recio-Blanco
and P. de Laverny fron Niza Observatory, and B.
Plez from Montpellier University. A technical note
is available describing the models used for the atmo-
spheres from which the synthetic spectra were calcu-
lated and which parameters were used ((Recio-Blanco
et al., 2005)). The library has a total of 9048 sam-
ples, the initial wavelength is 847.58 nm and the final
873.59 nm, the resolution is 0.0268 nm and the final
number of points per signal is 971.
Table 1: Parameters and value ranges.
Parameter Min Max
Teff 4500 7750
Logg -0.5 5
[Fe/H] -5 1
[α/Fe] -0.2 0.4
When the GAIA satellite becomes operative, the
RVS instrument will inevitably include noise from
various sources (sensitivity of the detectors, back-
ground noise near the source, instrumental noise, etc).
We have therefore considered the possibility of work-
ing with synthetic spectra that are modified by vari-
ous noise levels according to a simple model of noise,
white noise, and various SNR values: 5, 10, 25, 50,
75, 100, 150, 200 and ∞.
The dataset represents the total number of exam-
ples that will be used to carry out the first stage of the
experiment (comparison of results according to input
domains). This set was arbitrarily divided into two
subsets, in a proportion of 70%-30%; the first subset
will be used to train the algorithms, the second for
testing.
The above data were obtained through the par-
ticipation of our research team in the GAIA project.
The GAIA consortium has divided the tasks among
several coordination units (CUs). Our research team
belongs to CU8, the unit in charge of classification
tasks, which means that we shall focus on classifi-
cation through the parameterization of spectra from
individual stars. Our input information consists of
calibrated photometry, spectroscopy and astrometry,
data gathered by the satellite and used to estimate the
main astrophysical parameters of the stars: Teff, logg,
[Fe/H], and [α/Fe].
4 MATERIAL AND METHODS
We aim to use the genetic algorithm as a selector for
the characteristics of the signal (the spectrum) that
contain relevant information in order to be able to
predict a specific parameter. The genetic algorithm
is coded using a chain of ones and zeros (binary al-
phabet) in which each gene (bit) represents one of the
variables (points) from the input signal. In our case,
this input signal will be the result of the wavelet trans-
form described in section 2.
In order to represent the points of the signal that
are selected by a specific individual, we use the ge-
netic information of the chromosome as if it were a
mask which, when applied to the input signal, will
give us as a result the concatenation of the points for
the inputs that are indicated in the mask with a 1.
Those that contain a 0 will simply be rejected.
In order to carry out the tests with the genetic al-
gorithms and neural networks, we used a rack con-
taining 6 servers equipped with two Intel Xeon Quad-
Core processors and 16GB of RAM. For the auto-
matic creation, training, evaluation and storage of the
networks, we used the XOANE neural network tool
A COMBINATION OF CONNECTIONIST SYSTEMS AND EVOLUTIONARY COMPUTATION TECHNIQUES TO
ACHIEVE THE OPTIMAL DOMAIN FOR STELLAR SPECTRA SIGNAL PROCESSING
325

((Ordonez et al., 2007)), and in the case of the genetic
algorithms we have developed software based on the
Biojava library ((Down and Pocock, )), open code
software with a GNU licence. The Biojava library
provides us with a framework for the implementation
of the genetic algorithms, although the functions that
comprise the behaviour of the algorithm were imple-
mented by our research group. These functions are
cross-over, mutation, selection and evaluation of indi-
viduals (fitness).
4.1 Genetic Algorithm Configuration
The configuration of the genetic algorithm comprises
the specification of the strategies for selection, mu-
tation, crosses and evaluation, as well as the specific
parameters that govern their behaviour.
We applied a simple cross-over strategy in several
points to be configured (in this study we tested con-
figurations from one to three points), alternating the
segments of information into which each of the par-
ents is divided. The objective was to form two new
individuals with the different segments that resulted
from the selection of the cross-over points (justifica-
tion explaining why we used this cross-over strategy).
Due to the high dimensionality of the individuals
(having as many bits of information as the signal), if
we consider all of the individuals in the population as
candidates to be mutated, however low the probabil-
ity of mutation, all of the individuals will be mutated
at some stage. Also, if the probability is very low,
only a few bits will be mutated, and the change will
not be noticeable in the individual’s fitness value. For
this reason we reached a compromise by dealing with
two probabilities for mutation: one that allows us to
select the individuals from a population who will be
mutated (mutation candidates), and another that al-
lows us to determine if a gene is mutated or not at the
moment of applying the operator. In this way, only a
small number of individuals will be altered, and only a
small (although potentially significant) portion of the
information from the candidates to be mutated will be
modified.
With regard to the selection function, we used the
classic roulette algorithm, combined with an elitist
strategy: determining the percentage of the best in-
dividuals that will form a part of the next generation.
The usual selection operator is applied to the rest us-
ing the roulette method. We used this same strategy
to determine the selection of the chromosomes for the
population that will serve as a father, in order to com-
bine their genetic information in the crosses.
The specific values of the parameters for apply-
ing the strategies described are shown in table 2. We
Table 2: Parameters and value ranges.
Parameter Value
Number of cross-overs 3
Mutation probability (one gene) 0.1
Mutation probability (individual) 0.3
Number of generations 100
Training steps 100
Elitist selection proportion 15%
Symbol probability 50,00%
Parental selection proportion 100,00%
Number of threads per node 8
carried out numerous trials with different parameter
values. Those shown provide good results (see sec-
tion 6), investing reasonable computation times. With
regard to this aspect, we have two parameters that de-
termine the total time invested in the execution of the
genetic algorithm, which are the number of genera-
tions and the number of network training steps; this
function represents practically all of the algorithm’s
workload.
The fitness function is a particular type of objec-
tive function that quantifies the goodness of a solution
to a problem (chromosome) in a genetic algorithm,
so that in this way each chromosome can be com-
pared with the other components of the population.
A fitness function is better the closer one comes to
the intended objective. In our case, the objective was
to discover the most relevant points from a spectrum
in order to then train a neural network as optimally
as possible. For this reason, the fitness function is
based precisely on a network, and the fitness value is
the mean of the total number of errors as an absolute
value for the total number of selected tests (30%, see
section 3).
Training a neural network to the point of achiev-
ing the optimum configuration of weights in which
the network is considered to have been generalised
is always a costly task, and as a result so is the pro-
cess of computing the fitness function. In order to
obtain results within a reasonable timescale, experi-
ence has shown us that after 100 training stages the
network weights will provide us with a reliable ori-
entation if the training maintains a constant trend to-
wards the convergence minimum without any major
fluctuations. For this reason the fitness value we have
considered is the one obtained after completing this
number of iterations. If we consider a larger number
of iterations, we would expect to obtain a better result
from the genetic algorithm, although we would have
to accept the additional computing time involved.
Figure 2 shows the main stages of the genetic al-
gorithm. We began by generating an initial popula-
tion of 100 individuals or chromosomes, generating
IJCCI 2009 - International Joint Conference on Computational Intelligence
326

Figure 2: Flow of the genetic algorithm.
the population randomly using the mechanisms pro-
vided by the tool. Remember that we used a binary
alphabet, with a symbol probability that was equal for
all of the symbols, as shown in table 2. As a result,
at first the number of points is reduced to half, lead-
ing to an accelerated training time and test time. We
then carried out the initial evaluation of the individu-
als from the population, before iterating to obtain the
successive populations. The next step formed a part
of the iterative section: for the population resulting
from the previous iteration, the chromosomes were
selected that would form a part of the following pop-
ulation. As explained in this section, we applied the
cross and mutation operators and evaluated the new
individuals that were obtained, repeating the process
until reaching the maximum number of generations.
4.2 Fitness Function and Artificial
Neural Networks
Figure 3 shows a breakdown of the tasks carried out
in the fitness function. This function began with the
mask resulting from the genetic information of the in-
dividual we wished to evaluate, applying the trans-
formed data (see section 4), and obtaining the training
and test groups. The mask also provides us with in-
formation on the number of points that will comprise
the input. Taking this number of points, and as the
network will predict a single parameter, we then cre-
ated a neural network. The architecture of the neural
network is a feedforward with a single hidden layer,
and the number of process elements from each layer
depends on the inputs that the mask selects, as fol-
lows:
1. The number of process elements in the input that
are equal to the number of points selected by the
mask in the input signal.
2. For the hidden layer, we calculated the number
of process elements as the minimum between 200
and the number of inputs divided by two. The
number 200 was obtained based on experiments
with the complete signal, with no more being re-
quired in order to obtain the generalisation point.
3. Number of outputs equal to a process element (a
parameter to be predicted).
Figure 3: Evaluation process of the fitness function.
With regard to training, the online version of the
error retropropagation algorithm was chosen. This
training algorithm was chosen as a result of its proven
use when applied to data of this kind derived from
stellar spectra ((Bailer-Jones, 2008), (Kaempf et al.,
2005), (Bailer-Jones, 2000)). In order to apply the al-
gorithm a low learning rate was chosen (0.2), and 100
stages. The reason for the low learning rate is that
we had a large number of patterns and the training
process is carried out online, and so if we had used a
high rate this would have led to excessive fluctuation
of the weights.
Once the network was created and as we already
had the training and test groups, we then tested the
network for the 100 stages described above (Section
4.1). Once training was completed we obtained the
results for the tests as a whole, calculated the mean
errors for the test as an absolute value, and established
the inverse of this amount as the fitness value. It is
importantto take into account the fact that in this case,
the fitness valueis the inverse of the mean error so that
the highest values signify better individuals.
A COMBINATION OF CONNECTIONIST SYSTEMS AND EVOLUTIONARY COMPUTATION TECHNIQUES TO
ACHIEVE THE OPTIMAL DOMAIN FOR STELLAR SPECTRA SIGNAL PROCESSING
327
5 PARALLEL FITNESS
FUNCTION
In the description of the input data (Section 3) we em-
phasised the large amount of data available and its
dimensionality. The function that calculates the fit-
ness of each of the individuals in the genetic algo-
rithm is based on the training of the neural networks.
Against this framework and considering the nature of
the information being processed, the training of a net-
work becomes a highly costly task in terms of time
and computing resources. The sequential processing
of the fitness functions on a computer is not viable in
order to obtain results within a reasonable period of
time. In this study we looked for a way of carrying
out evaluations of the fitness functions for the new
individuals in a parallel way, attempting to take full
advantages of the computing power of the machines
that were available (see section 4).
The parallel calculations in this case were based
on the hardware features of the computers, each of
which have two Quad Core processors. This charac-
teristic makes it possible to launch concurrent threads
that calculate the fitness function separately and inde-
pendently from each other. Each of these threads is
executed independently, although controlled centrally
using a software module that acts as a pool. When the
genetic algorithm decides to evaluate an individual,
it sends the task to the pool, and if there are execu-
tion threads available it launches the fitness task. If at
the moment of launching the fitness function the pool
does not have any free threads, it queues the task until
one is available. In this way, and in an ideal situation
(not taking into account other bottlenecks in the ap-
plication such as access to the shared memory bus),
and considering the time dedicated to other times as
minimal (crosses, mutations, selected etc.), we would
divide the time required to pass from one generation
to another by the number of threads available, and
therefore also the total time spent on computing for
the complete algorithm.
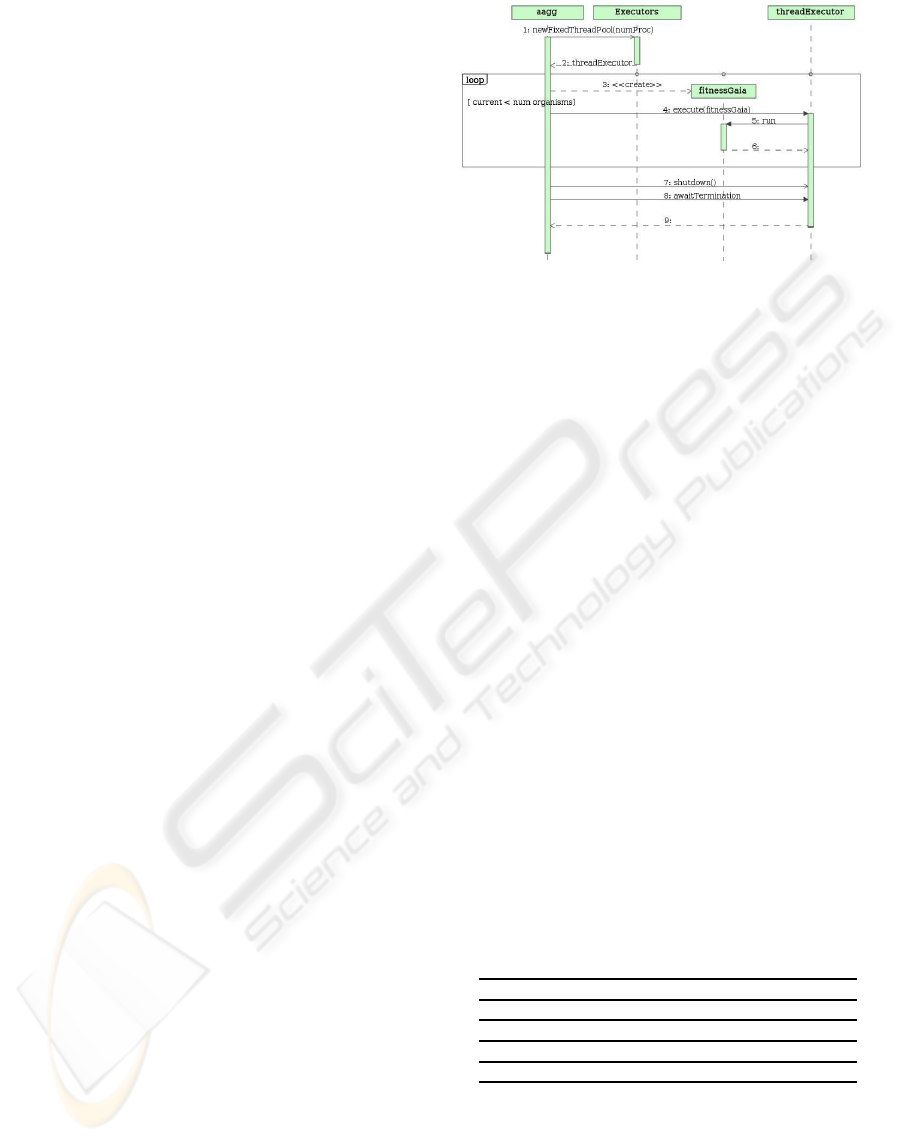
The way of interacting with the thread pool is as
shown in Figure 4: fitnessGaia is the fitness function
which in turn represents an execution thread. The ge-
netic algorithm orders the execution of fitness through
the threadExecutor object which plans the execution
of the concurrent threads, queuing their execution if
there are no free threads. In this Figure, after the loop
zone, we can see that the genetic algorithm waits for
the execution of all of the fitness functions to end be-
fore carrying out more tasks. It does so because the
fitness value is necessary for the selection operator,
which is the next operation to be carried out.
Figure 4: Message sequence to invoke the evaluation of a
chromosom.
6 RESULTS
After applying the genetic algorithm, the mask is ob-
tained that will select the relevant information from
the transformed signal, the result of applying the sig-
nal processing described in Section 2. The result-
ing series of data will provide us with the necessary
data for the training and testing of a neural network,
which this time we carry out in full (with 5000 train-
ing steps). As reference data for the training pro-
cess we selected two sub-groups: clean spectra and
SNR200, to which we applied the mask and network
training. After training the networks we applied the
mask to the reference group for the rest of the pat-
tern collections, i.e. all of the noise levels considered,
selecting the test patterns and calculating the results,
as shown in tables 3 and 4. As may be seen, based
on the results, executing the genetic algorithm with a
certain degree of noise in the spectra makes it possi-
ble to obtain slightly better results in comparison to
the same experiment carried out executing the genetic
algorithm with clean spectra.
Table 3: Mean errors when selecting the points with the
mask that results from applying genetic algorithms to clean
spectra.
Teff logg [Fe/H] [α/Fe]
SNR∞ 91.3775 0.1614 0.110966 0.0640266
SNR200 116.185 0.209743 0.13699 0.0852009
SNR75 160.716 0.286768 0.202252 0.11027
SNR10 485.427 0.999177 0.590903 0.219483
As the noise level increases, the results deterio-
rate. Despite this, they are especially relevant in the
presence of noise, as we can compare them with the
study (Ordonez et al., 2008) in which a comparison
is made of different signal processing techniques ap-
plied to spectra. The advantage of this perspective is
the reduction of the number of points in the signal and
IJCCI 2009 - International Joint Conference on Computational Intelligence
328
processing elements required to achieve a network
that generalises and provides us with results with ac-
ceptable margins of error.
−400 −300 −200 −100 0 100 200 300 400
0
50
100
150
200
250
300
350
400
450
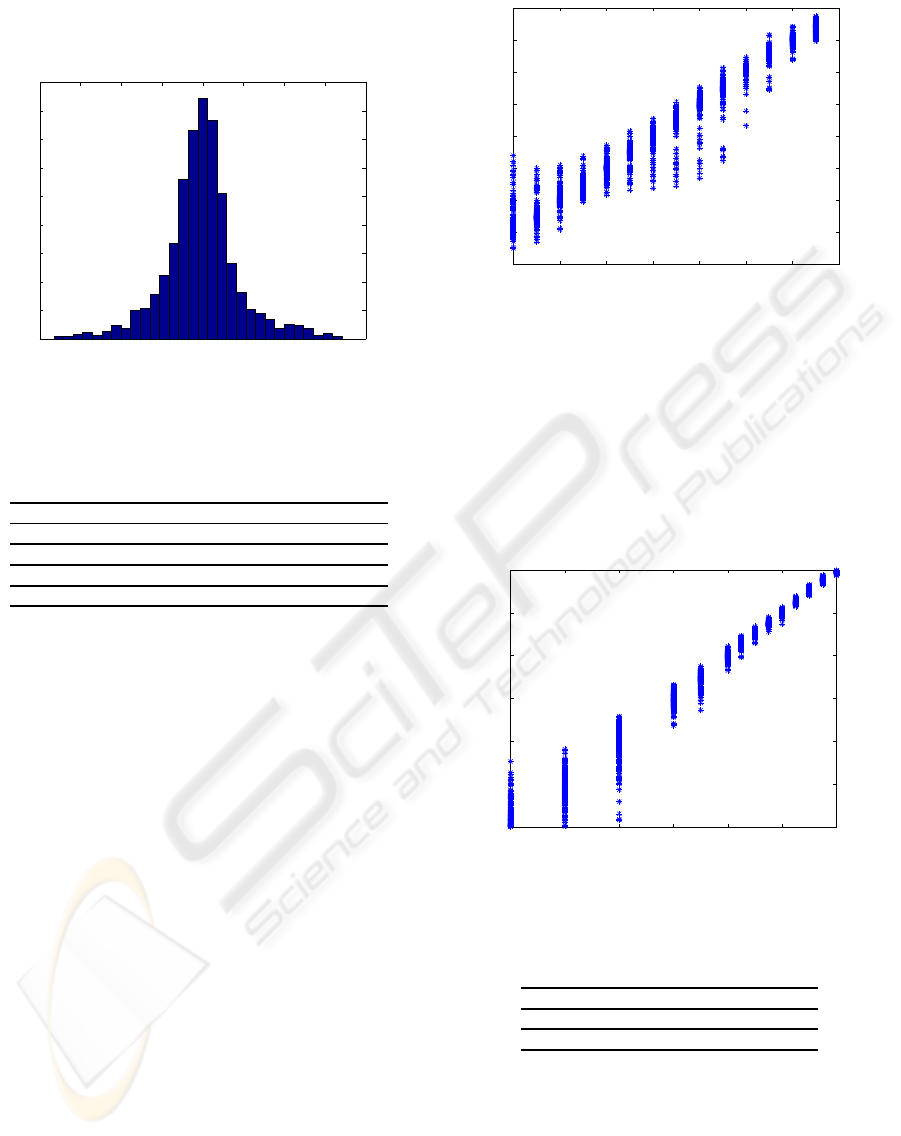
Figure 5: Error dispersion for temperature.
Table 4: Mean errors when selecting the points with the
mask that results from applying genetic algorithms to spec-
tra with SNR200.
Teff logg [Fe/H] [α/Fe]
SNR∞ 73.8318 0.16255 0.113446 0.0604846
SNR200 101.58 0.211558 0.143434 0.0797694
SNR75 142.944 0.294903 0.200731 0.111127
SNR10 437.162 0.944661 0.590903 0.221791
Another of the added advantages of this perspec-
tive for processing the information is that most of the
errors are concentrated around zero, as may be seen
in Figures 5 and 6, where there are also other exam-
ples with a higher error, but which represent less than
5% of the total. These Figures refer to the errors for
the best case (clean spectra) and the effective temper-
ature parameter. The concentration of the errors into
small margins means that the algorithm is more ro-
bust, because in most of the cases we are sure of hav-
ing good precision with a small margin of error. Table
5 shows additional information on this feature, show-
ing the standard deviation of the errors. Each of the
quantities shown should be studied within its context,
as an error of one unit in temperature (degrees Kelvin)
does not mean the same as an error in one unit in the
case of gravity. These results may be considered with
the study of Gulati and Ram´ırez (Gulati et al., 2001)
that analyses stellar spectra using genetic algorithms.
Figure 6 shows additional information, emphasis-
ing the fact that independently from the range of val-
ues of the parameter, the errors are highly concen-
trated around the correct value, and the fact that carry-
ing out the analysis on a cold star (4000K) or a hot star
(7750K) does not significantly influence the margins
of error. This does not occur with all of the parame-
ters; in the case of metallicity the opposite occurs for
4500 5000 5500 6000 6500 7000 7500 8000
4000
4500
5000
5500
6000
6500
7000
7500
8000
Figure 6: Error dispersion for temperature per parameter
value.
stars with low metallicity; the prediction is less re-
liable for stars with a high concentration of metallic
elements, as may be seen in Figure 7. For the rest of
the parameters the situation is similar to that of the ef-
fective temperature. As regards the dispersions with
the presence of noise in the spectra, as would be ex-
pected the error is more distributed and flattened in
the histogram shown in the Figure 5.
−5 −4 −3 −2 −1 0 1
−5
−4
−3
−2
−1
0
1
Figure 7: Error dispersion for metallicity per parameter
value.
Table 5: Typical deviation (σ) of the errors for all the pa-
rameters for the clean test spectra and SNR 75 case
Teff logg [Fe/H] [α/Fe]
SNR∞ 93 0.172 0.120 0.0.074
SNR75 167 0.28 0.226 0.136
7 CONCLUSIONS
Genetic algorithms have proved to be a useful tech-
nique in a lot of fields, also processing stellar spec-
tra (Gulati et al., 2001). We have applied genetic al-
gorithms and an artificial intelligence technique like
A COMBINATION OF CONNECTIONIST SYSTEMS AND EVOLUTIONARY COMPUTATION TECHNIQUES TO
ACHIEVE THE OPTIMAL DOMAIN FOR STELLAR SPECTRA SIGNAL PROCESSING
329

neural networks to process input signal (the stellar
spectrum) that allow us to select the relevant informa-
tion in it for each parameter. This is therefore the fun-
damental difference with a statistical algorithm such
as Principal Component Analysis, in which the rele-
vant information is selected based on its variability,
and without taking into account what we will use it
for. It is also necessary to take into account the fact
that we previously processed the signal based on dis-
crete wavelet analysis, as described in section 2.
The application of the genetic algorithm technique
is mainly aimed at reducing the dimensionality of the
signal, so that it may then reduce the time required
to parameterise the spectra, obtaining the result from
the neural network more quickly (due to the lesser
complexity of the network in terms of processing el-
ements). This aspect is of particular relevance in the
GAIA mission, as already mentioned in section 1, as
the aim is to classify millions of objects. Also, when
carrying out training, the algorithm converges earlier
as it only uses the information that is relevant in order
to study the specific parameter it is dealing with.
Reviewing the results we found a robust approach
to the parameterization of spectra, less demanding
with regard to computing time. The combination of
techniques allow us to use the advantages of both
techniques: genetic algorithms (dimensionality re-
duction and information selection based on the pa-
rameter to predict) and neural networks (noise toler-
ance, good error rates and low error dispersion).
ACKNOWLEDGEMENTS
Spanish MEC project ESP2006-13855-CO2-02.
REFERENCES
Bailer-Jones, C. (2000). Stellar parameters from very low
resolution spectra and medium band filters. Astron-
omy and Astrophysics, 357:197–205.
Bailer-Jones, C. (2008). A method for exploiting domain in-
formation in astrophysical parameter estimation. As-
tronomical Data Analysis Software and Systems XVII.
ASP Conference Series, XXX.
Department, E. S. O. Gaia: The galactic census problem.
Down, T. and Pocock, M. The biojava project.
Fiorentin, P., Bailer-Jones, C., Lee, Y., Beers, T., Sivarani,
T., Wilhelm, R., Allende, C., and Norris, J. (2007).
Estimation of stellar atmospheric parameters from
sdss/segue spectra. Astronomy and Astrophysics,
467:1373–1387.
Gulati, R. K., Ramirez, F., and Fuentes, O. (2001). Predic-
tion of stellar atmospheric parameters using instance-
based machine learning and genetic algorithms. Ex-
perimental Astronomy, 12(3):163–178.
Harinder, Gulati, and Gupta (1998). Stellar spectral classi-
fication using principal component analysis and artifi-
cial neural networks. MNRAS, 295:312–318.
Hippel, T. V., Allende, C., and Sneden, C. (2002). Auto-
mated stellar spectral classification and parameteriza-
tion for the masses. In The Garrison Festschrift con-
ference proceedings.
Hu, Y.-C. (2008). Nonadditive grey single-layer percep-
tron with choquet integral for pattern classification
problems using genetic algorithms. Neurocomputing,
72:331–340.
Kaempf, T., Willemsen, P., Bailer-Jones, C., and de Boer,
K. (2005). Parameterisation of rvs spectra with artifi-
cial neural networks first steps. 10th RVS workshop.
Cambridge.
Kinnebrock, W. (1994). Accelerating the standard back-
propagation method using a genetic approach. Neuro-
computing, 91(3):731–735.
Mallat, S. (1989). A theory for multiresolution signal de-
composition: The wavelet representation. Proc. IEEE
Trans on Pattern Anal. and Math. intel., 11(7):674–
693.
Morgan W.W., Keenan P.C., K. E. (1943). An atlas of stellar
sepctra with outline of spectral classification. Astro-
phys. monographs, University of Chicago Press.
Ordonez, D., Dafonte, C., Arcay, B., and Manteiga, M.
(2007). A canonical integrator environment for the
development of connectionist systems. Dynamics of
continuous, Discrete and Impulsive Systems, 14:580–
585.
Ordonez, D., Dafonte, C., Arcay, B., and Manteiga, M.
(2008). Parameter extraction from rvs stellar spec-
tra by means of artificial neural networks and spectral
density analysis. Lecture Notes in Artificial Intelli-
gence, 5271:212 – 219.
Recio-Blanco, A., de Laverny, P., and Plez, B. (2005). Rvs-
arb-001. European Space Agency technique note.
Rooij, A., Jain, L., and Johnson, R. (1996). Neural Network
Training Using Genetic Algorithms. World Scientific
Pub Co Inc, Singapore.
IJCCI 2009 - International Joint Conference on Computational Intelligence
330
