
2-CLASS EIGEN TRANSFORMATION CLASSIFICATION TREES
Steven De Bruyne and Frank Plastria
MOSI, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium
Keywords:
2-class Eigen transformation classification trees, 2C-ETCT, Classification, Supervised classification, Binary
classification, Linear classifiers, Remote clusters, Eigen transformations, Classification trees.
Abstract:
We propose a classification algorithm that extends linear classifiers for binary classification problems by look-
ing for possible later splits to deal with remote clusters. These additional splits are searched for in directions
given by several eigen transformations. The resulting structure is a tree that possesses unique properties that
allow, during the construction of the classifier, the use of criteria that are more directly related to classification
power than is the case with traditional classification trees.
We show that the algorithm produces classifiers equivalent to linear classifiers where these latter are optimal,
and otherwise offer higher flexibility while being more robust than traditional classification trees. It is shown
how the classification algorithm can outperform traditional classification algorithms on a real life example.
The new classifiers retain the level of interpretability of linear classifiers and traditional classification trees un-
available with more complex classifiers. Additionally, they not only allow to easily identify the main properties
of the separate classes, but also to identify properties of potential subclasses.
1 INTRODUCTION
Over the years many sophisticated classification algo-
rithms have been developed that outperform, classifi-
cation power wise, more traditional classifiers, such
as linear classifiers and classification trees. This does
not mean these traditional classifiers are now without
merit as both linear classifiers and classification trees
can easily be interpreted to understand which prop-
erties are relevant to differentiate between the groups
that are to be separated.
It can even be defended that either a linear clas-
sifier or a classification tree will perform relatively
well. In the cases where the instances of each class are
clustered together, linear classifiers should yield rea-
sonable results; in cases where the instances are more
scattered, classification trees will offer some of the
needed flexibility. There are, however, classification
problems intermediate between such extremes. The
basic assumption in classification problems is that in-
stances of the same class lie close together in the fea-
ture space. In an idealised case the instances of each
class approximate a normal distribution, an assump-
tion that is made when using the Naive Bayes algo-
rithm. In many cases however, the instances belong
to subclasses, which may not be known. The class
is then actually a union of subclasses, and its dis-
tribution may differ significantly from a single nor-
mal distribution, and rather be a mixture of several
such distributions. But since these subclasses belong
to the same class, they share similar properties and
their centres will often lie close together. As a con-
sequence, instances of the same class will still be
clustered together. For such a (binary) classification
problem the best classifiers will probably be a sin-
gle boundary, in most cases even a simple hyperplane,
which divides the feature space in two parts. If the dif-
ferences between the subclasses are large, however,
the instances of the same class may globally not be
all clustered together anymore, and a simple classifier
such as a hyperplane will not be flexible enough. A
classification tree on the other hand misses the fine-
tuning properties to separate the main groups opti-
mally as splits are only done on the attributes.
We therefore propose to extend the linear classi-
fier by adding the possibility to execute some addi-
tional splits, but limited to investigating some more
interesting directions only. To determine these inter-
esting directions we use eigen transformations such
as principal component analysis (Hotelling 1933; Jol-
liffe 1986), Fisher’s linear discrimant analysis (Fisher
1936) and principal separation analysis (Plastria, De
Bruyne and Carrizosa 2008). The first direction will
indicate the direction of the principal split, the others
will give an indication of where some additional clus-
ters may lie. Alternatively, the first direction might
251
De Bruyne S. and Plastria F. (2009).
2-CLASS EIGEN TRANSFORMATION CLASSIFICATION TREES.
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 251-258
DOI: 10.5220/0002266202510258
Copyright
c
SciTePress

also be determined by any algorithm yielding a linear
classifier. Such classifiers do not only allow to easily
identify the main properties of the different classes,
but also allow to identify properties of potential sub-
classes.
1.1 2-class Eigen Transformation
Classification Trees
The new algorithm we introduce in this paper is the
2-class eigen transformation classification tree (2C-
ETCT) and is based on the eigenvalue-based classi-
fication tree (EVCT) algorithm (Plastria, De Bruyne
and Carrizosa 2008).
The first step in building a 2C-ETCT is to trans-
form the feature space using an ordered transforma-
tion matrix completely or partially based on an eigen
transformation. As the classification power of the tree
can be estimated quite accurately as a consequence of
the a priori fixed structure of the tree, the 2C-ETCT
algorithm allows many transformations to be used si-
multaneously and the algorithm will select the best
performing transformation automatically. After the
feature space has been transformed, the tree is grown.
Due to the fact that the transformation ordered the
new features by relevance, the selection of the split
feature will be very straightforward. The split in the
top node is done based on the first feature, in the
nodes on the second level the splits are done based
on the second feature, etc. Theoretically, the depth of
the tree can equal the number of features, but if the
tree ends up being very large, the instances are prob-
ably too dispersed for this algorithm to outperform
existing methods. In these cases it is probably bet-
ter to use another tree algorithm. The algorithm will
outperform if the data set has the structure described
in the introduction and when the main split happens
in the top node and very few splits are needed for the
additional clusters.
Once a splitting feature has been chosen, the ac-
tual splits are calculated by taking the midpoint of two
consecutive instances that minimizes the number of
misclassifieds. The splits are made using this criterion
and not the more popular information gain (Quinlan
1993) or Gini index (Breiman et al. 1984), because
the goal is to base the construction as much as possi-
ble directly on the classification power. We also don’t
need to use the criteria to select a feature to split on.
After the tree is grown, it is pruned. As all 2C-
ETCTs are pruned versions of the largest 2C-ETCT,
we can use an internal cross-validation to determine
the optimal size of the tree. This way the entire train-
ing data can be used in all stages of the construction
of the tree in a statistically sound way and should lead
to less overfitting than for example the estimated er-
ror rates used in C4.5 classification trees for pruning
(Quinlan 1993). As we are using the same principle
to build and to evaluate the classifier, this technique
should yield reliable outputs.
1.2 Eigen Transformations
We will be using six eigen transformations, which
were also used in (Plastria, De Bruyne and Carri-
zosa 2008). The first three do not start from a sep-
arate classifier, but will retain the first eigenvector to
perform the first split. The first one is the unsuper-
vised principal component analysis (Hotelling 1933;
Jolliffe 1986). The second and third transformation
are the supervised Fisher’s linear discriminant anal-
ysis (Fisher 1936) and the principal separation com-
ponent analysis (Plastria, De Bruyne and Carrizosa
2008). The last three start with a separate first vector.
In practice one might prefer a vector based on a pow-
erful classifier such as support vector machines, but
here we choose a straightforward vector given by the
means of the instances of the two classes.
Using the following notations
• A : the matrix of p
A
columns representing the in-
stances of the first set
• B : the matrix of p
B
columns representing the in-
stances of the second set
• T = [A, B] : the matrix of p
T
= p
A
+ p
B
columns
representing the instances of both sets
• For a general matrix M ∈ R
d×p
M
– d : the original dimension of the data (number
of attributes)
– Mean(M) ∈ R
d×1
: the mean of the instances
of M
– Cov(M) ∈ R
d×d
: the covariance matrix of M
– Mom(M) ∈ R
d×d
: the matrix of second mo-
ments (around the origin) of M
– Eig(M) ∈ R
d×d
: the matrix of eigenvectors of
M
we use the following eigen transformation matrices R:
• the transformation matrix based on principal com-
ponent analysis
R = Eig(Cov(T ))
• the transformation matrix based on Fisher’s linear
discriminant analysis
S
W
=
p
A
Cov(A) + p
B
Cov(B)
p
T
S
B
= Cov(T ) − S
W
R = Eig(S
−1
W
S
B
)
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
252

• the transformation matrix based on principal sep-
aration components
R = Eig(Mom(A B))
where A B ∈ R
d×(p
A
p
B
)
is the matrix consisting
of all d-vectors a− b for any pair of d-vectors a ∈
A and b ∈ B.
• three transformation matrices based on the means
of both sets, combined with each of the aforemen-
tioned techniques
p = Mean(A) − Mean(B)
R
1
=
p
||p||
The remaining rows R
2..n
are the n − 1 first rows
of the aforementioned techniques after projection
of the instances on the hyperplane perpendicular
on R
1
.
2 2C-ETCT DATA STRUCTURE
A 2C-ETCT has a top node and a transformation ma-
trix corresponding to the eigen transformation that
yielded the best results. This matrix is used to trans-
form instances to the new feature space.
A node can have zero or two child nodes. If a node
has child nodes, it will delegate the request of classi-
fication of an instance to one of its child nodes chosen
thanks to the node’s split value on the feature of the
instance that corresponds to the level of the node. If
the node has no child nodes, it will classify the in-
stance as the expected class that corresponds with the
node.
A node also has ten node folds. These hold the
data that corresponds to the internal training and test
sets. This data is used during the construction of the
tree. Each node fold holds a split value and an ex-
pected class value based on the corresponding inter-
nal training data. The number of correct and incorrect
classified instances of the internal test data sets are
also stored in the node folds. This data is used to es-
timate the node’s classification power. It may be that
there is no data for a given node fold if for its inter-
nal training set the data is homogenous in a node at a
higher level.
Figure 1: Data Structure in UML.
3 2C-ETCT ALGORITHM
OVERVIEW
3.1 Tree.Create(data points)
Create training and test folds
For each dimension reduction technique do
Create the transformation matrix using
all data points
Create a new top
For each pair of transformed training and
test sets do
transformed training set ←
training set × transformation matrix
transformed test set ←
test set × transformation matrix
top.Grow(transformed training set)
top.Evaluate(transformed test set)
End for
top.PruneAfterEvaluation
End for
Select best top
transformed data ←
data points × transformation matrix
top.Calibrate(transformed data)
top.PruneAfterCalibration
3.2 Tree.Classify(data point)
transformed point ←
data point × transformation matrix
top.Classify(transformed point)
2-CLASS EIGEN TRANSFORMATION CLASSIFICATION TREES
253

4 INTERNAL FOLDS
Using the standard 10 folds would be an easy choice.
However, it has to be reconsidered whether this divi-
sion is still to be preferred when other factors come
into play. One also has to take into account the effect
on the computation time, whether the test folds are
sufficiently large for the algorithm to perform prop-
erly and if to avoid new overfitting. Therefore we’ve
chosen to use 2 5-fold divisions, to accommodate the
desirable properties. As data points are often offered
in a non-random order, the data points are first shuf-
fled before dividing them into folds. As a conse-
quence computational results are not necessarily the
same given repeated tests.
5 PHASES OF THE ALGORITHM
5.1 Grow
When a node receives a message to grow, it checks
whether the data points it received are not all of
the same class or that the last feature has not been
reached. If these conditions are met, a split value for
the current feature is calculated minimizing the num-
ber of misclassified instances. Then the data points
are split into two groups depending on their position
relative to the split value. The groups are passed to
their respective child node through a grow message.
If a child node does not yet exist, it is created. In case
a training set never reaches a specific node, the corre-
sponding node fold properties are not available.
5.2 Evaluate
During the evaluation phase the transformed test
folds are used. A node will compare the received
data points with the corresponding expected class
value, and the amount of corresponding and non-
corresponding points is stored for each fold. If the
node has children, the data points are divided accord-
ing to the corresponding split value and passed to the
child nodes to continue the evaluation phase.
5.3 Prune after Evaluation
The prune after evaluation is executed bottom-up;
thus the prune after evaluation is first executed by the
children, before it is by the parent node. Only the
existing node fold data is taken into account. The
number of correctly classified test data instances is
summed over all folds. If this total is not smaller than
the sum of the corresponding totals of the child nodes,
then the child nodes are pruned as they are assumed
to increase overfitting. In the other case the results of
the evaluation phase are changed to correspond with
these of the child nodes in order to reflect the classifi-
cation power of the node if it relies on its children.
5.4 Select Best Top
Now the classification power of the different top
nodes are compared and only the best top node and
its corresponding transformation matrix are kept.
5.5 Calibrate
During the calibration phase, the final split values and
expected classes for the nodes are calculated using the
entire training set. These are the values that are going
to be used during classification. The structure of the
tree remains unchanged during the calibration.
5.6 Prune after Calibration
If the entire offspring of a node has the same expected
class as the node itself, then these offspring nodes are
pruned.
6 EXAMPLE
Below one can find several figures illustrating differ-
ent parts of the algorithm. Note that here the number
of node folds has been limited to three and that only a
small part of the tree is depicted.
6.1 Grow
In figure 2 the node on level 3 received three grow
messages for each remaining part of the internal train-
ing sets that reached it. For each data set an expected
class value has been assigned based on the number of
instances of each class. If the instances of a training
set do not all belong to a single class, a split value
is calculated that minimizes the number of misclassi-
fied instances in its respective data set. This is done
for the first data set in figure 2. Consequently child
nodes of level 4 are created, which receive a grow
message with the respective subsets of the first train-
ing data set based on the split value of the node on
level three. The second training set was homogeneous
in the node on level three. As a consequence no split
value is computed and there will be no data available
for these node folds of the level 4 nodes. The third
training data set is dealt with in the same way as the
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
254
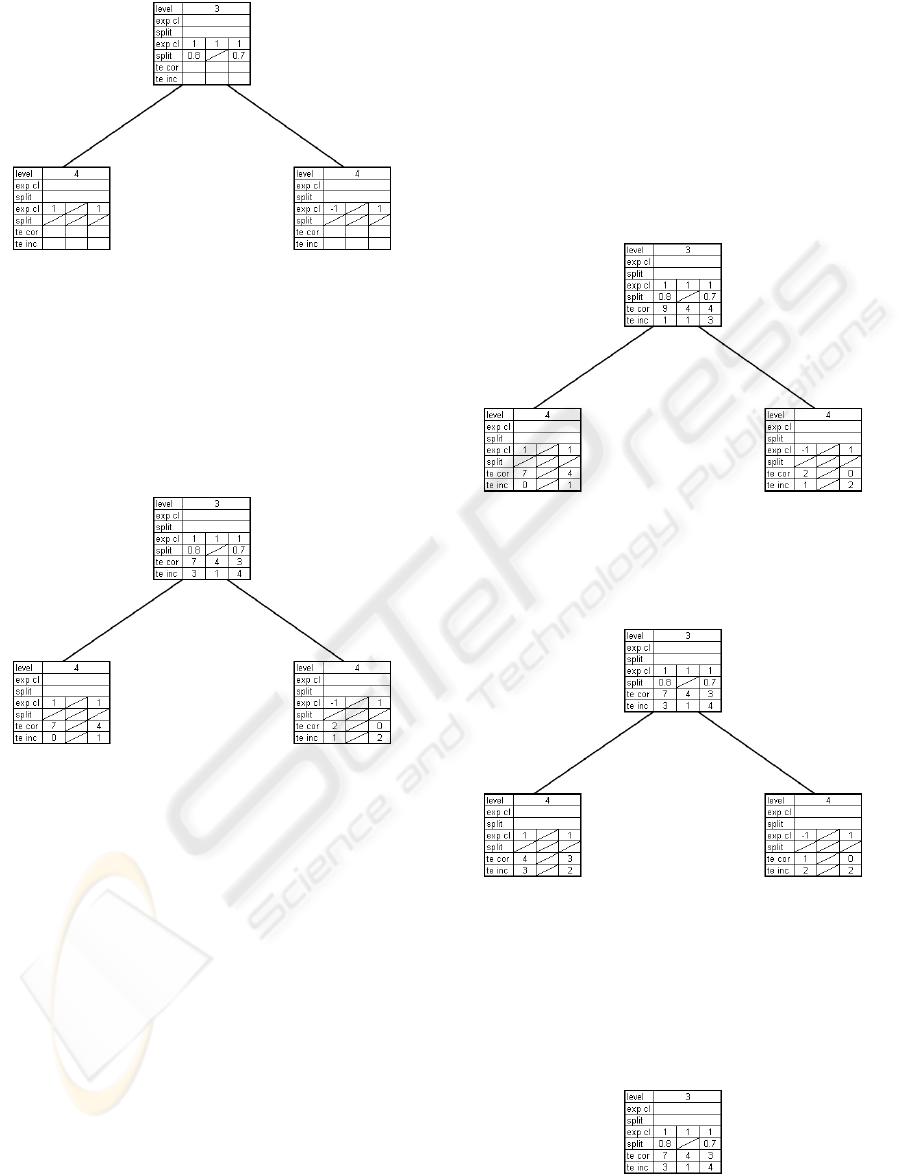
Figure 2: Example: grow.
first, except that no level 4 nodes need to be created
as they already exist.
6.2 Evaluate
After the tree has fully grown, the nodes are evaluated
with the test data sets as is illustrated in figure 3. For
Figure 3: Example: evaluate.
a node fold, the instances of its test data set are clas-
sified based on the expected class value of the node
fold. The number of correctly and incorrectly clas-
sified instances are stored. If a split value exists for
a given node fold, which is the case for the first and
the third node fold of the node with level 3, the test
sets are divided based on the split value and passed
on to the child nodes. If there is no split value as is
the case here for the second node fold, the data will
not be passed on to the child nodes and consequently
there will be no data available on that level for the
given node fold.
6.3 Prune after Evaluation
Figure 3 shows a node that receives a prune after eval-
uation message. To decide if the child node should be
pruned or not the evaluation data of the node folds is
used. The sum of the correctly classified instances of
the node folds for which data exists in the child nodes
are compared. In this case there are 13 instances cor-
rectly classified in the nodes of level 4. This is better
than the 10 correctly classified instances of the corre-
sponding node folds of the parent node. In this case
it is assumed that the child nodes improve the classi-
fication power of the parent node. Consequently, the
nodes are not pruned and the node fold data of the par-
ent node is updated to reflect the classification power
of its child nodes, which can be seen in figure 4.
Figure 4: Example: prune after evaluation 1.
Figure 5 shows another example of a node that re-
ceives a prune after evaluation message. In this case
Figure 5: Example: prune after evaluation 2.
the child nodes correctly classify 8 instances, which is
worse than the 10 correctly classified instances of the
corresponding node folds of the parent node. In this
case the child nodes will be pruned as can be seen in
figure 6.
Figure 6: Example: prune after evaluation 3.
2-CLASS EIGEN TRANSFORMATION CLASSIFICATION TREES
255

6.4 Calibrate
After the tree has been pruned, it is calibrated. Using
all the data available to the algorithm, the final split
values and expected class values are calculated for all
nodes as is shown in figure 7. This is similar to the
growth phase, except that no new nodes are created.
Figure 7: Example: calibrate.
7 NUMERICAL EXPERIMENTS
7.1 Without Additional Clusters
As the 2C-ETCT is an extension of a linear classifier,
we first check its performance as a linear classifier.
Therefore we construct data sets with different dimen-
sions of 500 instances belonging to 2 classes that both
have a normal distribution. We compare the classi-
fication power of the 2C-ETCT with a Naive Bayes
(Bayes) classifier that expects this kind of distribution
and a support vector machine (SVM) (Vapnik 1995)
that should also perform well on these problems. Ex-
cept for the 2C-ETCT results, the results were ob-
tained using Weka (Witten and Frank 2005)
If the 2C-ETCT performs as we expect it to, there
should not be a significant difference with the Bayes
and the SVM classifiers. We can indeed see in table
1 that there is no such significant performance differ-
ence.
We also added the results when classifying with
a C4.5 tree (Quinlan 1993) and we can see it is less
suited for these kinds of problems than the other
classifiers. But more interestingly, we also observe
that the C4.5 tree suffers from increasing overfitting
when the dimensionality rises and the space gets more
sparse as a consequence, which is not the case with
the 2C-ETCT indicating that it is a more robust clas-
sifier.
Table 1: 10-fold cross-validations on data sets without ad-
ditional clusters.
d 2C-ETCT Bayes SVM C4.5
5 91.6% 91.8% 90.8% 85.8%
6 95.4% 95.4% 95.8% 91.0%
7 95.6% 95.8% 95.6% 88.2%
8 96.8% 97.8% 97.2% 89.8%
9 99.0% 98.6% 98.2% 88.4%
10 99.0% 98.6% 98.2% 88.4%
11 98.0% 98.0% 98.2% 86.8%
7.2 With Additional Clusters
Next we check the performance of the 2C-ETCT algo-
rithm on classification problems with some additional
clusters. Again we construct data sets with different
dimensions of around 500 instances belonging to 2
classes. 80% of the instances are distributed in the
same way as the data sets without additional clusters.
The remaining 20% is used to create addititional clus-
ters. There are d clusters of each class.
The clusters were not placed purely at random for
several reasons. First, the impact of the position of
the clusters would be so large, that it would not be
possible to compare the results over the different data
sets. Second, clusters behind the main cluster of the
opposite class deviate too much from the concept that
the clusters share common properties with the main
cluster. Third, clusters that are too close to the main
cluster or behind the main cluster of the same class
don’t really influence the problem and can not be con-
sidered as separate clusters. Fourth, if clusters of the
same class are too close to one another they start to
form one cluster. In order to take these concerns into
account and to avoid giving an large advantage or dis-
advantage to any of the algorithms, we apply the fol-
lowing constraints. The centres of the clusters are po-
sitioned on the hyperplanes going through the centres
of the main clusters perpendicular to the vector given
by the centres of the main clusters. Each cluster is
also placed at fixed distance from the previous cluster
perpendicular to all previously used directions. This
way the clusters are well dispersed within the con-
straints. Half of the clusters around one of the main
classes are of the opposite class and the other half
are of the same class. If d is odd there is one clus-
ter more of the opposite class. If a cluster is placed
in direction v, a cluster of the opposite class is placed
around the opposite main cluster in direction −v. This
gives an advantage to the linear classifiers as clus-
ters can be positioned closely to one hyperplane and a
small change to the hyperplane can move one cluster
to the other side, without having too much influence
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
256

on its position relative to the other clusters. This also
avoids some degenerate cases for the C4.5 classifica-
tion trees. These data sets have a disadvantage for lin-
ear classifiers as there are clusters, but an advantage as
the clusters are positioned favourably for these algo-
rithms. For the C4.5 classification trees the existence
of the clusters gives them an advantage, but the fact
the 80% of the instances belong to only two clusters
gives it a disadvantage. The 2C-ETCT has the ad-
vantage that the particular clusters with some smaller
clusters favours the algorithm, but not all of such a(n)
(unrealistically) large number of clusters can be found
by the algorithm and this property with the specific
position of the clusters also has a negative impact on
the determination of the first eigenvector and conse-
quently on all others.
In table 2 we can see that the 2C-ETCT now sig-
nicantly outperforms the Bayes and SVM classifiers,
which can be explained by the fact that the 2C-ETCT
can identify some of the clusters without introducing
more overfitting. Due to the largely normally dis-
tributed nature of the groups, the C4.5 tree still cannot
outperform the other classifiers although it has a big
advantage with the existence of the additional clus-
ters.
Table 2: 10-fold cross-validations on data sets with addi-
tional clusters.
d 2C-ETCT Bayes SVM C4.5
5 88.5% 86.7% 85.7% 83.7%
6 90.0% 82.2% 82.8% 84.8%
7 88.1% 86.7% 86.5% 82.3%
8 90.2% 85.9% 87.8% 83.3%
9 89.3% 88.9% 88.5% 84.1%
10 91.0% 89.0% 88.2% 85.7%
11 90.4% 89.0% 88.4% 82.0%
7.3 Real Life Example
Figure 8 shows the visualisation of a 2C-ETCT us-
ing the first two principal mean components. The
data set in question is the glass data set from the UCI
Machine Learning Repository (Newman et al. 1998).
The instances of the data set belong either to the win-
dow glass class or the non-window glass class. Both
classes consist of several subclasses, which are not
known for this version of the data set. As the sub-
classes of each of the classes have similar properties
in most cases, the two groups can be clearly distin-
guished. However, the fact that not all properties are
shared by the subclasses manifests itself by the ex-
istence of smaller clusters further removed from the
main group. It can be seen in table 3 that the 2C-
ETCT outperforms a linear classifier as this is not able
to handle the smaller clusters. The C4.5 on the other
hand cannot exploit the mainly normally distributed
classes and will therefore also be outperformed by the
2C-ETCT.
Figure 8: 2C-ETCT of the glass data set using principal
mean components.
Table 3: 10-fold cross-validations on UCI glass windows
data set.
d p 2C-ETCT Bayes SVM C4.5
9 214 94.8% 89.7% 92.1% 93.0%
8 CONCLUSIONS
We introduced eigen transformation based classifica-
tion trees that are meant to be extensions of linear
classifiers. Alongside we proposed a parameterless
algorithm using an internal cross-validation to com-
pute these 2C-ETCTs. We have shown that the re-
sulting trees are equivalent to linear classifiers where
these are optimal. In these cases the 2C-ETCT has
also proven to outperform and to be more robust than
traditional classification trees. We have also shown
that in cases, both artificial and real, where the in-
stances of a class are largely normally distributed ex-
cept for some small clusters the 2C-ETCT can signif-
icantly outperform both traditional linear classifiers
and classification trees. These extended classifiers
do not only offer more flexibility than the aforemen-
tioned traditional classifiers, but also offer a level of
2-CLASS EIGEN TRANSFORMATION CLASSIFICATION TREES
257

interpretability lacked by more complex classifiers.
Additionally, they do not only allow to easily identify
the main properties of the separate groups, but also to
identify properties of potential subclasses.
ACKNOWLEDGEMENTS
This work was partially supported by the research
project OZR1372 of the Vrije Universiteit Brussel.
REFERENCES
Breiman L., Friedman J.H., Olshen R.A., Stone C.J. (1984)
Classification and regression trees. Wadsworth, Bel-
mont
Fisher R.A. (1936) The Use of Multiple Measurements in
Taxonomic Problems. Annals of Eugenics 7: 179-188
Hotelling H. (1933) Analysis of a complex of statistical
variables into principal components. Journal of Edu-
cational Psychology 24: 417–441.
Jolliffe I.T. (1986) Principal component analysis. Springer,
Berlin
Plastria F., De Bruyne S., Carrizosa E. (2008) Dimensional-
ity Reduction for Classification: Comparison of Tech-
niques and Dimension Choice. Advanced Data Min-
ing and Applications, Tang C., Ling C.X., Zhou X.,
Cercone N.J., Li X. (Eds.) Lecture Notes in Artificial
Intelligence 5139: 411-418, Springer, Berlin
Quinlan J.R. (1993) C4.5 Programs for Machine Learning.
Morgan Kaufmann
Newman D.J., Hettich S., Blake C.L., Merz C.J. (1998).
UCI Repository of machine learning databases
http://www.ics.uci.edu/∼mlearn/ MLRepository.html.
Irvine, CA: University of California, Department of
Information and Computer Science.
Vapnik V. (1995) The nature of statistical learning theory.
Springer, New York
Witten I.H., Frank E. (2005) Data Mining: Practical ma-
chine learning tools and techniques, 2nd Edition Mor-
gan Kaufmann, San Francisco, 2005. Weka software:
http://www.cs.waikato.ac.nz/∼ml/weka/index.html
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
258
