
Hierarchical Control System for Complex
Dynamical Plants
Yuri V. Mitrishkin
1
and Rodolfo E. Haber
2
1
Bauman Moscow State Technical University
Second Baumanskaya St. 5, 105005 Moscow, Russia
2
Instituto de Automatica Industrial, CSIC, Madrid, Spain
Abstract. The paper is devoted to a concept of hierarchical control for complex
dynamical plants and suggests architecture of control system consisting of ro-
bust, adaptive, and intelligent levels. Intelligent features of the proposed system
are mostly concentrated at the third level incorporated into self-organizing al-
gorithm and decision making approach realized by developers and process en-
gineers. Some results are presented from present groundwork of research per-
formed and future work is outlined. Case study has been chosen from the area
of plasma magnetic and kinetic control in tokamak-reactor.
1 Introduction
Recent advances in control strategies, communications, hard and soft-computing
technologies have favored an increasing trend towards the new generation of net-
worked control systems for complex plants. The proposal described herein will ad-
dress the development of scalable control methods and systems in accordance with
the Information and Communication Technologies (ICT) Work Programme of the
European Commission (EC), the objective ICT-2009 3.5a: Engineering of Networked
Monitoring and Control systems with target outcome of Foundations of Complex
Systems Engineering [1].
The engineering of networked monitoring and embedded systems is a challenge
common to a wide scope of strategic application domains for complex processes. The
project is focused on complex automation problems aiming at development of control
theory and a framework for future technological and scientific breakthroughs in the
conjunction with state-of-the-art of control theory, distributed and embedded compu-
tations, communications and intelligent systems. Proposal multidisciplinary fields
include control theory (multi-sensor systems approach, linear and nonlinear stability,
robust and adaptive control, and so forth), computer science (reconfigurable architec-
tures, high-performance computations, signal processing, combinatorial optimization,
and so forth), networking and monitoring application-specific issues (data fusion,
fault tolerant and so forth), network theory (dynamic QoS management), and artificial
intelligence-based techniques (fuzzy, neural and neuro-fuzzy systems).
Mitrishkin Y. and Haber R. (2009).
Hierarchical Control System for Complex Dynamical Plants.
In Proceedings of the International Workshop on Networked embedded and control system technologies: European and Russian R&D cooperation,
pages 56-65
Copyright
c
SciTePress

Interdisciplinary and multidisciplinary essence of this proposal relies on all hierar-
chical levels of control, from local controllers linked to physical objects (processes)
up to networked monitoring and complete managing of complex processes. On the
one hand, a key issue is to make control systems easily implemented, self-
configuring, and self-optimizing. Proposal goes beyond the current state-of-the-art
improving the computational efficiency and the ways in which embedded systems
interact with the physical world. On the other hand, the system has to guarantee fault-
tolerance and efficiency of networking and monitoring.
To meet the goal stated by the EC a three level hierarchical control system was
suggested in Bauman Moscow State Technical University to be applied to solve con-
trol problems of complex dynamic plants in science, engineering, and industry.
2 Philosophy of Hierarchical Control
The project is focused on design and development of scalar (Single-Input/Single-
Output: SISO) and multivariable (Multi-Input/Multi-Output: MIMO) control systems
based on scalable control algorithms for uncertain time-varying nonlinear complex
dynamic plants. The major innovation of the proposal implies the elaboration of a
new methodology for designing hierarchical adaptive self-organizing control systems
to be applied to complex production processes, such as: plasma energy release, chem-
ical and biological processes, casting in metallurgy, oil refinery, and so forth.
2.1 Features of Hierarchical and Heterarchical Control
Today’s technologies are enabling complex processes to become more and more
autonomous. Industry and academia have investigated a wide range of decentralized
control architectures ranging from hierarchical decomposition to a completely
decentralized (heterarchical) approach where individual controllers are assigned to
subsystems and may work independently or may share data and information.
The main disadvantage of heterarchical approaches is that global optima cannot be
guaranteed and predictions of the system’s behaviour can only be made at the aggre-
gate level. Hierarchical and heterarchical architectures lie at opposite ends of the
distributed control architectures spectrum. The hierarchical approach is rigid and
suffers from many of the shortcomings of the centralized approach, whereas it pro-
vides clear advantages in terms of overall system coordination alternatively. Despite
the large amount of results related with hierarchical control methods, much work has
still to be done to extend many theoretical results (stability, performance, robustness)
nowadays available from advanced control implementations (
H
∞
, MPC) and non-
traditional control strategies (e.g., neurofuzzy control systems) to the hierarchical
structure [2]. In order to synthesize hierarchical control laws, the knowledge of suit-
able simulation functions is useful. However, an effective characterization of the
simulation functions and of the associated interfaces for complex plants is not
straightforward [3].
Hierarchical control can be used to integrate extra information (in addition to that
57
concerning the usual control-loop variables such as output, error, etc.) into the control
decision-making process. In many situations a hierarchical approach is an advanta-
geous option for process optimization, instead of sophisticated design and implemen-
tation of high-performance low-level controllers.
Thanks to its own structural essence, the hierarchical control scheme ensures flex-
ibility and compatibility with other controllers that have already been installed. It has
other strong points as well, such as the relatively low cost of investments in improv-
ing automation scheme performance, the possibility of exploiting already-installed
low-level regulation systems, and the relatively low cost of measurement systems
which makes hierarchical control a wise choice from economic and practical view-
points.
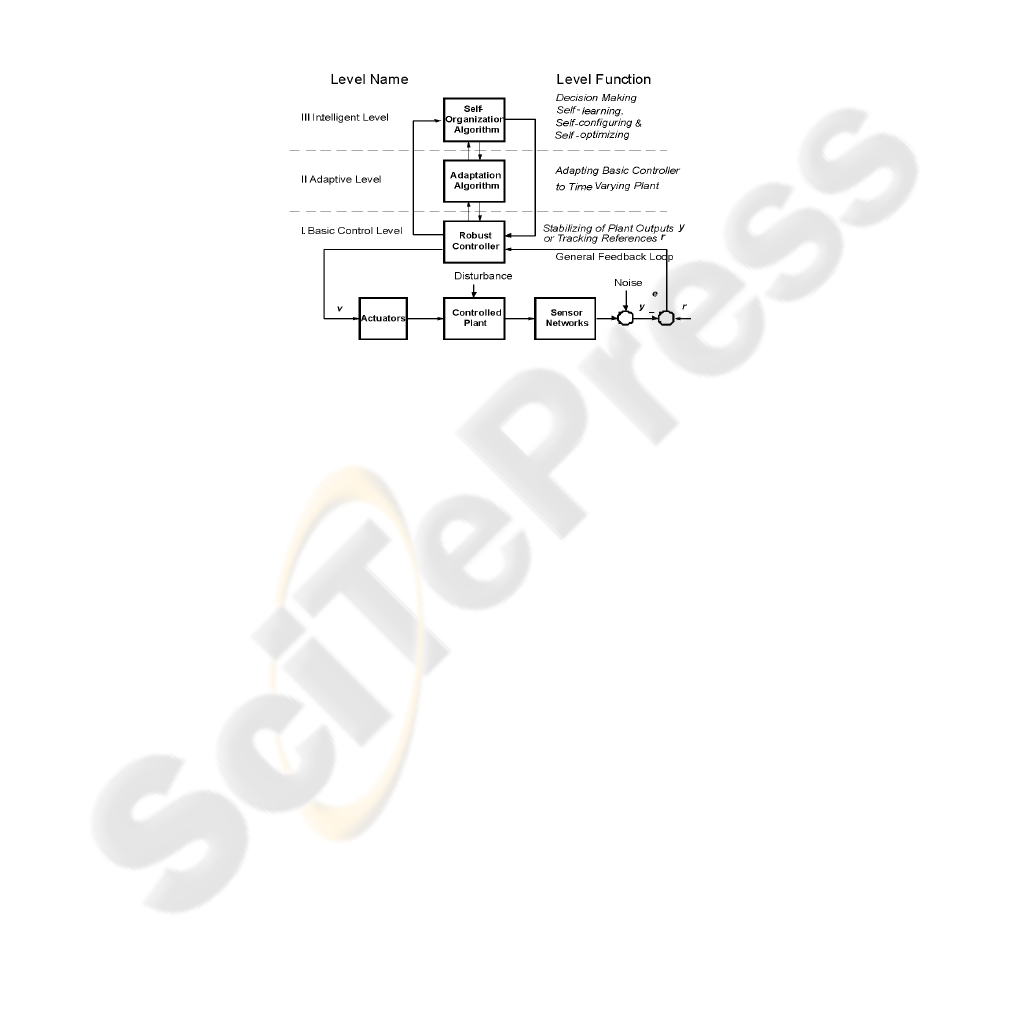
Fig. 1. General configuration of three levels hierarchical control system
2.2 Idea of Three Levels Hierarchical Control System
Whenever hierarchical levels are to be applied, goals and tasks must be broken down
into levels of resolution. The architecture of the suggested hierarchical control system
is composed of three levels (Fig. 1).
Basic Control Level (I) contains a controlled process under Disturbance, Actuators,
Sensor Networks, and a multivariable Robust Controller capable of operation under
process uncertainties. Here r is reference action, y is plant output containing Sensor
Networks outputs with Noise and measurement inaccuracy, e is an error between
reference r and plant output y which is related to the controller input, v is Actuators’
input. This level is designed to monitor the process itself and its environment in order
to undertake corresponding actions to reject internal and external disturbances and
noise in output signals being measured. General Feedback Loop of Basic Control
Level is to solve one of two control problems: Stabilizing of Plant Output y or Track-
ing of Reference r. In the case of unstable process General Feedback Loop is to stabil-
ize plant dynamics. Sensor Networks monitor processing conditions, and if plant
input actions are required, changes are made by the Actuators. Robust Controller
provides General Feedback Loop capability to work in the presence of plant uncer-
tainties and is to secure acceptable trade-off between robust stability and robust per-
formance.
58

Adaptive Level (II) contains scalable Adaptation Algorithm which provides
Adapting Basic Controller to Time-Varying Plant Parameters and Disturbance to
achieve the goal of adaptation at this level. Adaptive Level helps Basic Control Level
to accomplish closed-loop system trade-off at each discrete moment and to provide
the best possible dynamical features of General Feedback Loop.
Intelligent Level (III) with Self-Organizing, Self-Learning, Self-Configuring, Self-
Optimizing, and Decision-Making algorithms has more complex functions. This level
is organized by rule base (knowledge base), working memory (facts), and inference
engine (rule engine). The rule base contains declarative rules defined by user; the
facts are instances of templates to be stored in working memory. The inference engine
matches the facts against rules, fires rules, and executes associated actions. The ac-
tions are taken by the Robust Controller and carried out by Actuators at Basic Control
Level. Adaptation to changing conditions or optimization of control processes is
achieved at Self-Organizing Level by changing the structure of Robust Controller,
switching separate subsystems on or off, qualitatively changing algorithms of Adap-
tive Level, changing connections between subsystems and their subordination
schemes, and so on.
2.3 Levels Cooperation and Decision Making
The basic difference between Adaptive and Self-Organizing Levels means that Adap-
tive Level (II) provides tuning of the Basic Control Level (I) mostly through quantita-
tive changes, whereas Self-Organizing Level (III) adjusts lower levels (II) and (I)
through qualitative changes. In other words, Self-Organization Algorithm dynamical-
ly reconfigures system architectures. At this level self-learning models may be used to
get on-line plant parameter and structure changes in order to predict optimal control
at each discrete moment.
It is extremely complicated and unreliable to delegate decision making functions
at level (III) to artificial intelligent agent. At this level the decision making proce-
dures are assumed to be done by systems developers and process engineers in accor-
dance with the best choice of control algorithms which are the most effective in the
case studies and industry applications to complex plants under control (plasma in
thermonuclear reactors, oil refinery plants and the like) taking into account expert
system database and data knowledge.
3 Statements of Control Problems and Implementation
A number of new important complex control problems have to be studied, discussed
and formulated to achieve control goals of acceptable trade-off between robust sta-
bility and performance of feedback systems. The problem statements concern the
stabilization and tracking process output signals, optimal distribution of process pa-
rameters in space in the presence of non-modeled process dynamics, unobserved
disturbances, nonlinearities, in particular saturations, wideband insufficiently known
noise in output signals, non-minimum-phase dynamics, and time-varying parameters.
59

To solve these control problems a set of approaches from linear and nonlinear control
theory will be explored and developed to achieve scalable
H
∞
robust, decoupling,
model predictive, adaptive, hierarchy, cascade, soft-computing based control (e.g.,
neuro-fuzzy control systems), and facilitate decision-making in new appropriate com-
binations within continuous and discrete time of the three-level hierarchic control
system (Fig. 1). Scalable control algorithms mean that the algorithms may be genera-
lized to any numbers of controlled plant inputs, outputs, and space states.
The main scientific and technical contributions of the project imply the integration
and synergy achieved as a result of the implementation of advanced control methods,
relevant computational strategies and state-of-the-art technologies for embedded and
networked systems. In the process of hierarchical structure control systems design the
synthesis, analysis, and numerical modeling approaches are proposed to be performed
in MATLAB/SIMULINK environment. The controllers to be designed are planned to
be implemented in a test bed with primary objective to evaluate functionality of con-
trol systems in real time. The test bed should consist at least of two basic electronic
blocks: dynamic process model under control and feedback hierarchical controller
which interconnection should demonstrate advantages of scalable control algorithms
to be elaborated and modern high-performance computations in real time.
4 Case Study of Plasma Energy Release
In order to advance the suggested control approaches plasma energy release case
study is planned to be investigated on plasma in tokamaks. Nuclear fusion should be a
new source of practically inexhaustible energy and tokamaks are the leaders in ther-
monuclear energy release area. The plasma control systems under investigation are
supposed to be applied to ITER (International Thermonuclear Experimental Reactor).
It is an intense and challenging time for ITER to design the whole set of coupled
plasma magnetic and kinetic control systems. Magnetic control systems have to pro-
vide accurate control of plasma magnetic configuration [4] and stabilize plasma
against the main MHD modes [5]. Kinetic control systems are to control power fusion
and power flow to the diverter [6, 7] as well as profiles of plasma kinetic parameters:
plasma current, temperature, and density [8].
Reliable control of plasma shape and current in ITER is still a challenging prob-
lem because of necessity of controller change during transition from limiter to diver-
tor phases, existence of separate loop to suppress plasma vertical speed of unstable
vertical position, currents saturations in poloidal field (PF) coils, and so forth. Plasma
tokamak configuration with a free boundary defined by currents in PF active coils and
passive contours is described by vector Kirchhoff equation [9] and Grad-Shafranov
nonlinear partial differential equation [9, 10]. These equations together with equation
of magnetic field diffusion into plasma are realized numerically by DINA plasma-
physics code [9].
Plasma magnetic control in ITER is planned to be realized by two-loops control
system presented in Fig. 2: fast scalar loop stabilizes plasma vertical speed around
zero and slower multivariable loop tracks (on ramp-up and ramp-down phases) and
stabilizes (on quasi-stationary phase) plasma shape and current [11].
60

Fig. 2. Two-loops control system: K
BD
is block-diagonal controller, MC is multivariable main
converter, VSC is vertical stabilization converter, F
d
is derivative filter, F is filter for plasma
shape, current and control currents, g is a vector of gaps between separatrix and the first wall,
I
p
is plasma current.
Plasma in ITER is a MIMO plant that has 11 inputs (voltages on 11 superconductive
magnetic coils) and 19 outputs (6 gaps, plasma current, currents in 11 PF coils, plas-
ma vertical speed). At the moment we have simulation results on DINA code of ap-
plication of three control methodologies for plasma magnetic control specifically
cascade decoupling with PI controllers,
H
∞
, and Model Predictive Control (MPC).
Decoupling approach gave a chance to track plasma current (Fig. 3a) and gaps (Fig.
3b) on the plasma current ramp up phase [11]. In particular
H
∞
and MPC control
systems were applied at plasma current flat-top phase (Fig. 4a) where MPC showed
better performance at minor disruptions but
H
∞
system had larger robust stability
margin [12].
The fragments of plasma magnetic control were applied for ITER reference sce-
nario 2 with plasma current on flat-top of 15 MA. Multivariable robust controller
design (Fig. 1) on level (I) with adaptation on level (II) is proposed to be done for the
whole plasma discharge of plasma current ramp-up, ramp-down, and at quasi statio-
nary stages. It is planned to be applied for ITER reference scenario 2 and for reversed
share scenario 4 of plasma current of 9 MA.
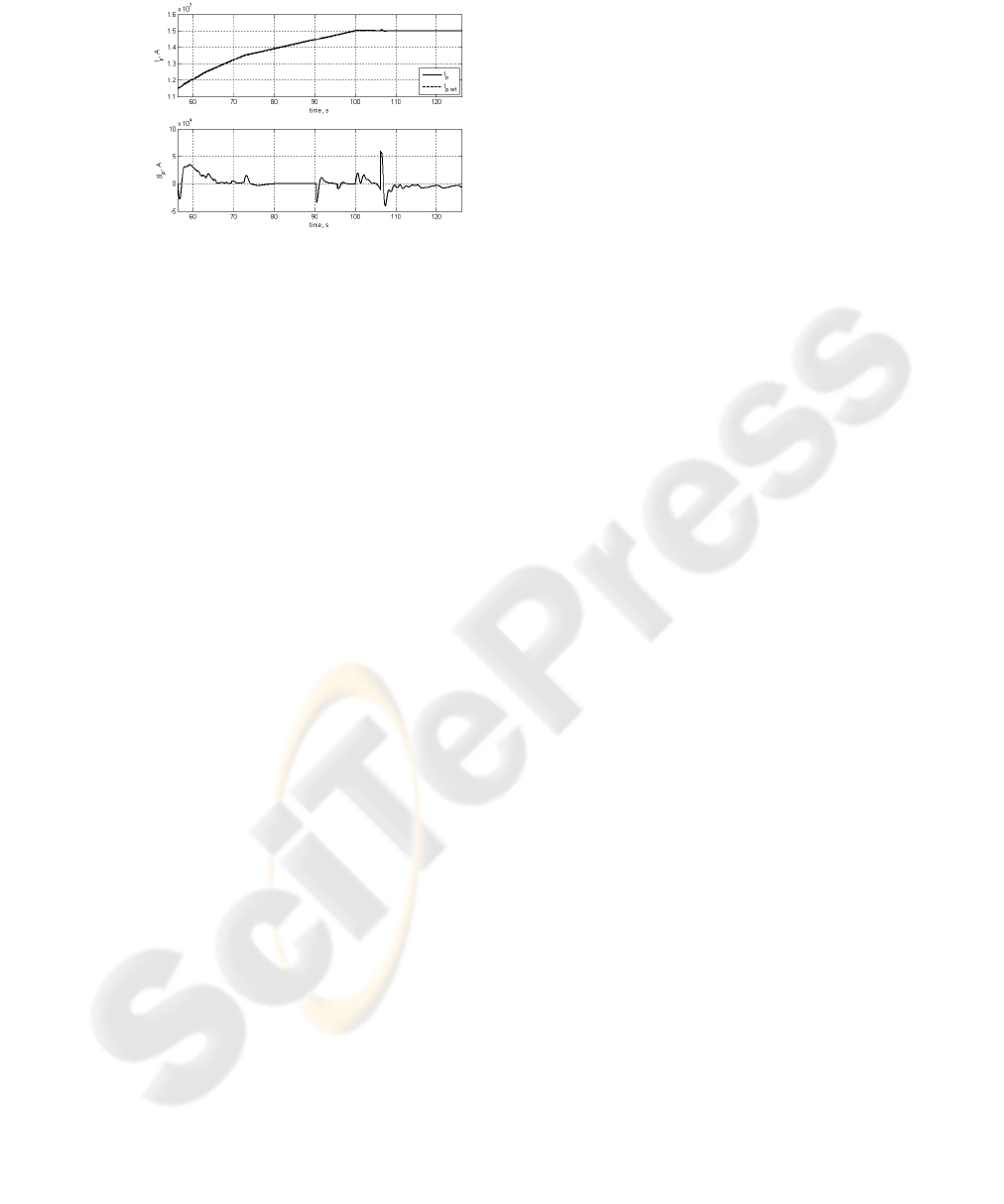
The project control methodologies are planned to be advanced to solve plasma ki-
netic control problem as well. Plasma kinetic control means creation and maintenance
of optimal plasma current, temperature, and density profiles by means of additional
heating sources. Such regimes are necessary for stationary operation of tokamak-
reactors. As the first step in this direction the kinetic plasma model was created on the
base of diffusion equation which dynamically connects 5 inputs from power of heat-
ing sources for current drive and 5 outputs that are densities
p
J
of plasma current at 5
predetermined points of tokamak major radius [13]. For this kinetic model the identi-
fication problem was solved at zero frequency and then
55
×
-multivariable controller
was designed with the usage of decoupling principle and PI diagonal entries. Control-
ler was simulated on the original kinetic model and showed capability of work in the
range of plasma temperature on magnetic axis from 100 eV to 5 keV. Transient
process from initial plasma current profile to designated positions at the given points
as well as relaxation process after disconnection of the feedback are presented in Fig.
4b [13].
61

One of the main obstacles of plasma control systems design is to solve lineariza-
tion and identification problems aiming at controller synthesis. In order to improve
results on this way one can try to apply modern techniques with the help of neural
networks and fuzzy logic. These approaches alone or combined (neurofuzzy) are able
to model complex plants without knowledge of plant First Principle Equations using
black-box or grey-box modeling approaches. In some cases these models are obtained
from experimental input/output data or using simulation data from very complicated
original plant models.
5 Intelligent Identification and Control Algorithms
Classic and non-traditional control strategies will be combined in order to incorporate
self-* capabilities. Internal-model control (IMC) is a well-established approach to
design controllers in which the process model is explicitly used in the control-system
design procedure [14]. The use of the IMC paradigm theoretically guarantees control
system robustness and stability in the presence of external disturbances. The actual
roots of MPC are indeed in the IMC paradigm.
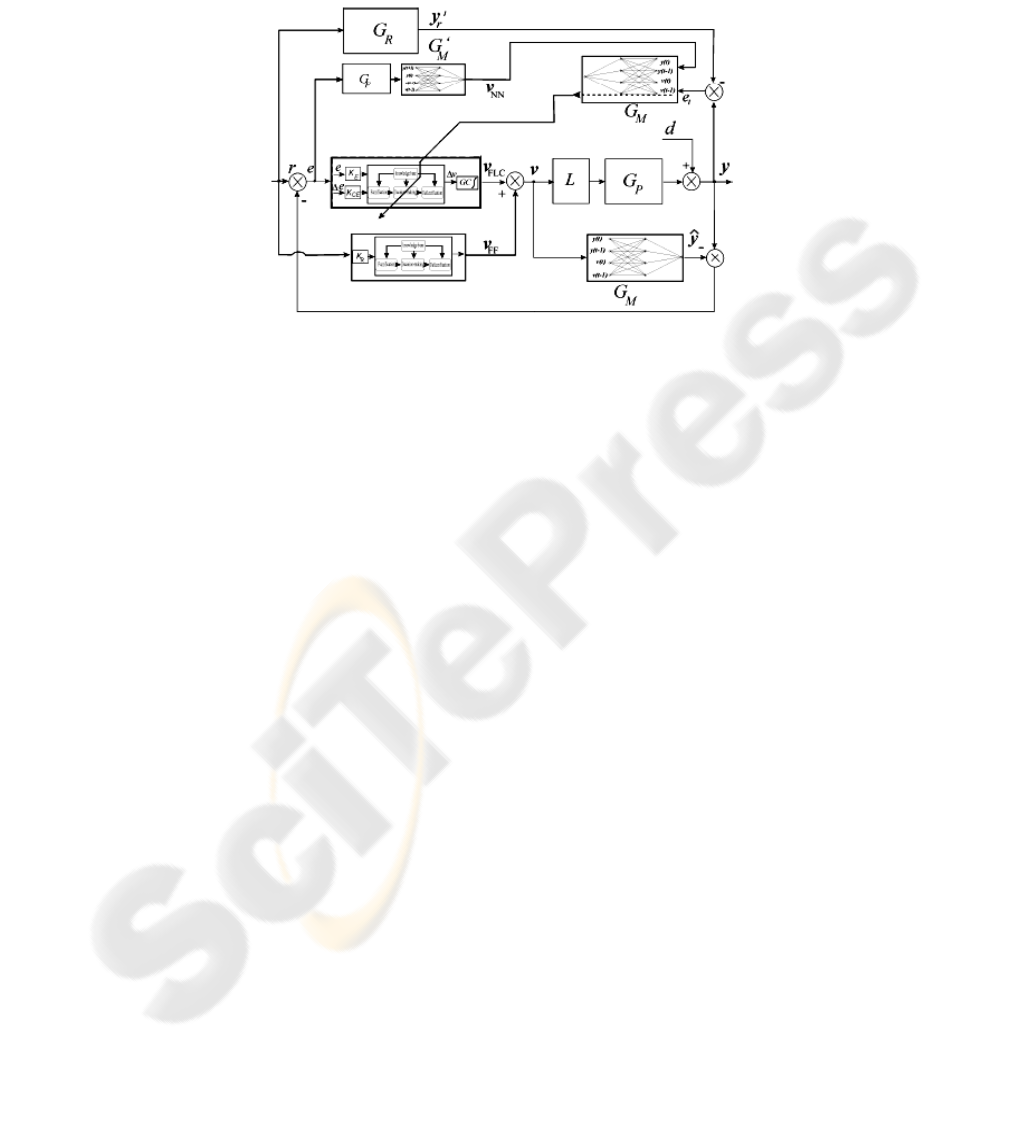
A block diagram of an internal model control based on Artificial Neural Networks
(ANN) and Fuzzy Logic (FLC) is depicted in Fig. 5. All disturbances are considered
to take place in the process output. In the figure
M
G
denotes a model of the process
(direct model),
'
M
G is an approximate inverse of
M
G ,
F
G is a low-pass filter, L
denotes dead-time process plus network-induced delay,
p
G denotes the process. The
main assumptions are that an approximate reference model
r
G is required and a max-
imum allowable delay (bounded delays) is known to deal with uncertainties and non-
linearities of the controlled process and delays in the corresponding network-based
application.
Construction of the IMC system consists of two stages: (i) selection of a control-
ler (usually the inverse model) to achieve perfect control and (ii) the introduction of a
filter.
First an ANN is trained to learn the dynamics of the process and is therefore given
known input- and output-data sets. So, one of the neural-network models developed is
selected as a basis for IMC control. The inverse model is obtained on the basis of
generalized training. Therefore, the network is trained off-line to minimize quadratic
criteria
()
2
1
ˆ
( ) () () .
M
t
J
vt vt
θ
=
=−
∑
Another ANN is trained to learn the inverse dynamics of the process and to work
as a nonlinear controller. The back-propagation of error is applied for tuning
[
]
,
F
CF
KK
θ
=
corresponding to the input scaling factors of the fuzzy block that can
replace the inverse model (Fig. 5). The goal is the optimal setting of input scaling
factors
[
]
,
F
CF
KK
to ensure that the overall system follows the reference signal
'()
r
yt closely. If inverse model actually describes the inverse dynamic of the plant,
there will be a perfect cancellation and we should attempt to find
[
]
,
F
CF
KK
θ
=
such
63
that
(
)
(
)
NN FLC
vtv t≅ . Using the forward model one can estimate the Jacobians:
(
)
(
)
(
)
(
)
ˆ
/1 /1yt vt yt vt∂∂−≅∂∂−⎡⎤ ⎡⎤
⎣⎦ ⎣⎦
.
Fig. 5. A tailored scheme based on internal model control with self-learning, feedforward
compensation and self-optimization based on ITAE criterion via error back-propagation
An important issue is the stopping condition to avoid overestimating
[
]
,
F
CF
KK
θ
=
. The best course is to use the integral of time multiplied by the abso-
lute value of error (ITAE) criterion to optimize the transient response and to penalize
lengthy transients
()
dttetJ
T
∫
⋅=
0
2
. The ITAE criterion of
2
J
is selected to obtain
smaller overshoots and oscillations, which are quite harmful for the cutting tools used
in machining.
It is important to remark that hybridization of FLC with ANN can also be applied
in the IMC-based approach using other neuro-fuzzy inference systems [15].
6 Conclusions
The concept of three levels hierarchical control system was presented and discussed
namely: philosophy of hierarchical control, statement of control problems, implemen-
tation, case study of plasma energy release, and intelligent identification and control
algorithms.
The project will result in the creation of new process models, procedures of their
identification and reduction, efficient, robust, predictable, and safe ICT control me-
thodologies, scalable control algorithms, and high-performance controllers for the
problem oriented hierarchical systems under consideration. Scientific, engineering,
and industrial results will be accumulated in the data and knowledge bases with accu-
rate classification, qualitative and quantitative assessment, and generalization.
64

References
1. European Commission C 6827 of 17 November 2008. Work Programme 2009. Coopera-
tion, Theme 3. ICT – Information and Communication Technologies (2008)
2. Scattolini, R.: Architectures for distributed and hierarchical Model Predictive Control - A
review. Journal of Process Control, 19 (2009) 723-731
3. Girard, A., Pappas, G.J.: Hierarchical control system design using approximate simulation.
Automatica, 45 (2009) 566-571
4. Lister, J.: Magnetic control of a tokamak equilibrium. Proc. of International Workshop:
Control for Nuclear Fusion, Eindhoven Univ. of Technology, the Netherlands (2008)
www.wtb.tue.nl/cnf/home.php
5. Katsuro-Hopkins, O., Bialek, J., Maurer, D.A., Navratil, G.A.: Enhanced ITER resistive
wall mode feedback performance using optimal control techniques. Nuclear Fusion, 47,
(2007) 1157–1165
6. Portone A.: The ITER Plasma control challenge. Proc. of International Workshop: Control
for Nuclear Fusion, Eindhoven Univ. of Technology, the Netherlands (2008)
7. Leonov, V.M., Mitrishkin, Y.V., Zhogolev, V.E.: Simulation of Burning ITER Plasma in
Multi-Variable Kinetic Control System. Proc. of the 32 EPS Plasma Physics Conference,
Tarragona, Spain (2005) ID P5.078
8. Labordel, L., Mazon, D., Moreau D., et al.: A model-based technique for integrated real-
time profile control in the JET tokamak. Plasma Phys. Control. Fusion, 47 (2005) 155–183
9. Khayrutdinov, R.R., Lukash, V.E.: Studies of Plasma Equilibrium and Transport in a To-
kamak Fusion Device with the Inverse-Variable Technique. Journal Comp. Physics, 109
(1993) 193–201
10. Wesson, J.: Tokamaks. 2nd edn. Clarendon Press, Oxford (1997)
11. Mitrishkin, Y., Korostelev, A., Dokuka, V., Khayrutdinov R.: Design and Modelling of
ITER Plasma Magnetic Control System in Plasma Current Ramp-Up Phase on DINA Code.
Submitted to 48
th
IEEE Conference on Decision and Control, Shanghai (2009)
12. Mitrishkin, Y.V., Korostelev A.Y.: System with Predictive Model for Plasma Shape and
Current Control in Tokamak. Control Sciences, 5 (2008) 22-34 (in Russian)
13. Mitrishkin Y., Dokuka V., Khayrutdinov R., Vertinski A.: Identification and Control of
Plasma Current Profile in Tokamak-Reactor. Proc. of VII International Conference System
Identification and Control Problems, SICPRO’08, Moscow, Institute of Control Sciences
(2008) 1796-1813, ISBN 978-5-91459-002-0
14. Morari, M., Zafiriou, E.: Robust process control. Prentice Hall, Englewood Cliffs, NJ
(1989)
15. Gajate, A., Haber, R.E.: Internal Model Control Based on a Neurofuzzy System for Net-
work Applications. A Case Study on the High-Performance Drilling Process, IEEE Trans-
actions on Automation Science and Engineering, 6 (2) (2009) 367-372
65
