
Dynamic Routing using Real-time ITS Information
Ali R. Güner, Alper Murat and Ratna Babu Chinnam
Department of Industrial and Manufacturing Engineering, Wayne State University
4815 Fourth St. Detroit, MI 48202, U.S.A.
Abstract. On-time delivery is a key performance measure for dispatching and
routing of freight vehicles in just-in-time (JIT) manufacturing environments.
Growing travel time delays and variability, attributable to increasing congestion
in transportation networks, are negatively impacting the efficiency of JIT
logistics operations. Recurrent congestion is one of the primary reasons for
delivery delay and variability. In this study, we propose a stochastic dynamic
programming formulation for dynamic routing of vehicles in non-stationary
stochastic networks subject to recurrent congestion. Results are very promising
when the algorithms are tested in a simulated network of Southeast-Michigan
freeways using historical Intelligent Transportation Systems (ITS) data.
1 Introduction
Supply chains that rely on just-in-time (JIT) production and distribution require
timely and reliable freight pick-ups and deliveries from the freight carriers in all
stages of the supply chain. However, road transportation networks are experiencing
ever growing travel time delays, which greatly hinders all travel and certainly the
freight delivery performance. Travel time delays are mostly attributable to the so
called ‘recurrent’ congestion that, for example, develops due to high volume of traffic
seen during peak commuting hours. The standard approach to deal with congestion is
to build additional ‘buffer time’ into the trip (i.e., starting the trip earlier so as to end
the trip on time). Intelligent Transportation Systems (ITS) are providing real-time
traffic data (e.g., lane speeds and volumes) in many urban areas. In-vehicle
communication technologies, such as satellite navigation systems, are also enabling
drivers’ access to this information en-route. In this paper, we precisely consider JIT
pickup/delivery service, and propose a dynamic vehicle routing model that exploits
real-time ITS information to avoid recurrent congestion.
Our problem setting is the non-stationary stochastic shortest path problem with
recurrent congestion. We propose a dynamic vehicle routing model based on a
Markov decision process (MDP) formulation. Stochastic dynamic programming is
employed to derive the routing ‘policy’, as static ‘paths’ are provably suboptimal for
this problem [1]. The MDP ‘states’ cover vehicle location, time of day, and network
congestion state(s). Recurrent network congestion states and their transitions are
estimated from the ITS historical data. The proposed framework employs Gaussian
mixture model based clustering to identify the number of states and their transition
rates, by time of day, for each arc of the traffic network. To prevent exponential
G
¨
uner A., Murat A. and Chinnam R. (2009).
Dynamic Routing using Real-time ITS Information.
In Proceedings of the 3rd International Workshop on Intelligent Vehicle Controls & Intelligent Transportation Systems, pages 66-75
Copyright
c
SciTePress

growth of the state space, we also recommend limiting the network monitoring to a
reasonable vicinity of the vehicle.
The rest of the paper is organized as follows. Survey of relevant literature is given
in section 2. Section 3 establishes modeling recurrent congestion and dynamic vehicle
routing for the problem. Section 4 presents experimental settings and discusses the
results. Finally, section 5 offers some concluding remarks.
2 Literature Survey
Shortest path problems with stochastic and time-dependent arc costs (STD-SP) are
first studied by Hall [1]. Hall showed that the optimal solution has to be an ‘adaptive
decision policy’ (ADP) rather than a single path. Hall [1] employed dynamic
programming (DP) approach to derive the optimal policy. Later, Fu [2] discussed
real-time vehicle routing based on the estimation of immediate arc travel times and
proposed a label-correcting algorithm as a treatment to the recursive relations in DP.
Waller and Ziliaskopoulos [3] suggested polynomial algorithms to find optimal
policies for stochastic shortest path problems with one-step arc and limited temporal
dependencies. For identifying paths with the least expected travel (LET) time, Miller-
Hooks and Mahmassani [4] proposed a modified label-correcting algorithm. Miller-
Hooks and Mahmassani [5] extends [4] by proposing algorithms that find the
expected lower bound of LET paths and exact solutions by using hyperpaths.
All of the studies on STD-SP assume deterministic temporal dependence of arc
costs, with the exception of [3] and [6]. Polychronopoulos and Tsitsiklis [7] is the first
study to consider stochastic temporal dependence of arc costs and to suggest using
online information en route. They defined environment state of nodes that is learned
only when the vehicle arrives at the source node. They considered the state changes
according to a Markovian process and employed a DP procedure to determine the
optimal policy. Kim et al. [8] studied a similar problem as in [7] except that the
information of all arcs are available real-time. They proposed a DP formulation where
the state space includes states of all arcs, time, and the current node. They stated that
the state space of the proposed formulation becomes quite large making the problem
intractable. They reported substantial cost savings from a computational study based
on the Southeast-Michigan’s road network. To address the intractable state-space
issue, Kim et al. [9] proposed state space reduction methods. A limitation of Kim et
al.[8], is the modeling and partitioning of travel speeds for the determination of arc
congestion states. They assume that the joint distribution of velocities from any two
consecutive periods follows a single unimodal Gaussian distribution, which cannot
adequately represent arc travel velocities for arcs that routinely experience multiple
congestion states. Moreover, they also employ a fixed velocity threshold (50 mph) for
all arcs and for all times in partitioning the Gaussian distribution for estimation of
state-transition probabilities (i.e., transitions between congested and uncongested
states). As a result, the value of real-time information is compromised rendering the
loss of performance of the dynamic routing policy. Our proposed approach addresses
all of these limitations.
67

3 Modeling
3.1 Recurrent Congestion Modeling
Let the graph
()
,GNA=
denote the road network where
N
is the set of nodes
(intersections) and
ANN⊆×
is the set of directed arcs between nodes. For every
node pair,
',nn N∈
, there exists an arc
(
)
,'ann A
≡
∈
, if and only if, there is a road
that permits traffic flow from node
n
to 'n . Given an origin,
0
n
-destination,
d
n
node
(OD) pair, the trip planner’s problem is to decide which arc to choose at each decision
node such that the expected total trip travel time is minimized. We formulate this
problem as a finite horizon Markov decision process (MDP), where the travel time on
each arc follows a non-stationary stochastic process.
An arc is labeled as observed if its real-time traffic data (e.g., velocity) is available
through the traffic information system. An observed arc can be in
1r
+
+
∈Ζ different
states that represent arc’s traffic congestion level at a time. We begin with discussing
how to determine an arc’s congestion state given the real-time velocity information
and defer the discussion on estimation of the congestion state parameters to Section 4.
Let
(
)
1i
a
ct
−
and
(
)
i
a
ct
for i=1,2,...,r+1 denote the cut-off velocities used to determine
the state of arc a given the velocity at time
t on arc
a
,
(
)
a
vt
. We further define
(
)
a
s
t
as the state of arc
a
at time
t
, i.e.
(
)
{
}{}
Congested at level
a
s
tii==
and can
be determined as:
(
)
(
)
(
)
(
)
{}
1
,if
ii
aaaa
s
t i c t vt ct
−
=≤<
. For instance, if there are two
congestion levels (e.g.,
12r
+
=
), then the states will be i.e.,
() { } {}
Uncongested 0
a
st==
and
(
)
{
}
{
}
Congested 1
a
st==
and the travel time is
normally distributed at each state.
We assume the state of an arc evolves according to a non-stationary Markov
chain. In a network with all arcs observed,
(
)
St
denotes the traffic congestion state
vector for the entire network, i.e.,
(
)
(
)
(
)
(
)
{
}
12 ||
, ,...,
A
St s t s t s t=
at time
t
. For
presentation clarity, we will suppress (
t
) in the notation whenever time reference is
obvious from the expression. Let the state realization of
(
)
St
be denoted by
()
s
t
.
It is assumed that arc states are independent from each other and have the single-
stage Markovian property. In order to estimate the state transitions for each arc, two
consecutive periods’ velocities are modeled jointly. Accordingly, the time-dependent
single-period state transition probability from state
(
)
a
s
ti
=
to state
(
)
1
a
s
tj+=
is
denoted with
()
(
)
{
}
1| ()
ij
aaa
P
st jst i t
α
+= ==
. The transition probability for arc
a
,
()
ij
a
t
α
, is estimated from the joint velocity distribution as follows:
()
()
(
)
(
)
(
)
(
)
(
)
() () ()
11
1
<111
<
iij j
aaaa a a
ij
a
ii
aaa
ctVtctc t Vt ct
t
ctVtct
α
−−
−
≤∩+<+<+
=
≤
68

Let
()
,1
a
Ttt+
denote the matrix of state transition probabilities from time
t
to
time
1t + , then we have
()
(
)
,1
ij
aa
ij
Ttt t
α
⎡
⎤
+=
⎣
⎦
. Note that the single-stage Markovian
assumption is not restrictive for our approach as we could extend our methods to the
multi-stage case by expanding the state space [10]. Let network be in state
(
)
St
at
time
t
and we want to find the probability of the network state
(
)
St
δ
+
, where
δ
is
a positive integer number. Given the independence assumption of arcs’ congestion
states, this can be formulated as follows:
()()
()
()
1
|()|()
A
aa
a
P
St St Ps t s t
δδ
=
+= +
∏
.
Then the congestion state transition probability matrix for each arc in
δ
periods
can be found by the Kolmogorov’s equation:
()
(
)
(
)
(
)
,1...
ij ij ij
aaa a
ij ij ij
Ttt t t t
δα α α δ
⎡
⎤⎡ ⎤ ⎡ ⎤
+= × + ×× +
⎣
⎦⎣ ⎦ ⎣ ⎦
.
With the normal distribution assumption of velocities, the time to travel on an arc
can be modeled as a non-stationary normal distribution. We further assume that the
arc’s travel time depends on the congestion state of the arc at the time of departure
(equivalent to the arrival time whenever there is no waiting). It can be determined
according to the corresponding normal distribution:
(
)
(
)
(
)
(
)
2
,, ~ ,, , ,,
aaa
tas N tas tas
δμσ
,
where
(
)
,,
a
tas
δ
is the travel time;
(
)
,,
a
tas
μ
and
(
)
,,
a
tas
σ
are the mean and the
standard deviation of the travel time on arc
a
at time
t
with congestion state
(
)
a
s
t
.
3.2 Dynamic Routing Model with Recurrent Congestion
We assume that the objective of our dynamic routing model is to minimize the
expected travel time based on real-time information where the trip originates at node
0
n
and concludes at node
d
n
. Let's assume that there is a feasible path between
()
0
,
d
nn
where a path
()
01
,.., ,..,
kK
pnn n
−
=
is defined as sequence of nodes such that
1
(, )
kkk
ann A
+
≡∈
,
0,.., 1kK=−
and
K
is the number of nodes on the path. We
define set
1
(, )
kkk
ann A
+
≡
∈
as the current arc set of node
k
n
, and denoted with
()
k
CrAS n
. That is,
()
{
}
1
:(,)
kkkkk
CrAS n a a n n A
+
≡≡ ∈
is the set of arcs emanating
from node
k
n
. Each node on a path is a decision stage (or epoch) at which a routing
decision (which node to select next) is to be made. Let
k
nN
∈
be the location of k
th
decision stage,
k
t
is the time at k
th
decision stage where
{
}
1,...,
k
tT∈
,
1K
Tt
−
>
. Note
that we are discretizing the planning horizon.
While optimal dynamic routing policy requires real-time consideration and
projection of the traffic states of the complete network, this approach makes the state
space prohibitively large. In fact, there is little value in projecting the congestion
69

states well ahead of the current location. This is because the projected information is
not different than the long run average steady state probabilities of the arc congestion
states. Hence, an efficient but practical approach would tradeoff the degree of look
ahead (e.g., number of arcs to monitor) with the resulting projection accuracy and
routing performance. This has been very well illustrated in Kim et al. [9]. Thus we
limit our look ahead to finite number of arcs that can vary by the vehicle location on
the network. The selection of the arcs to monitor would depend on factors such as arc
lengths, value of real-time information, and arcs’ congestion state transition
characteristics. For ease of presentation and without loss of generality, we choose to
monitor only two arcs ahead of the vehicle location and model the rest of the arcs’
congestion states through their steady state probabilities. Accordingly, we define the
following two sets for all arcs in the network.
(
)
k
ScAS a
, the successor arc set of arc
k
a
,
(){ }
11 12
:(,)
kkk kk
ScAS a a a n n A
++ ++
≡≡∈
, i.e., the set of outgoing arcs from the
destination node (
1k
n
+
) of arc
k
a
.
(
)
k
P
ScAS a
, the post-successor arc set of arc
k
a
,
()
{
}
22 23
:(,)
kkk kk
P
ScAS a a a n n A
++ ++
≡≡∈
i.e., the set of outgoing arcs from the
destination node (
2k
n
+
) of arc
1k
a
+
.
Since the total trip travel time is an additive function of the individual arc travel
times on the path plus a penalty function measuring earliness/tardiness of arrival time
to the destination node, the dynamic route selection problem can be modeled as a
dynamic programming model. The state,
(
)
12
,
,,
kk
kk
kaa
nts
++
∪
, of the system at
k
th
decision stage is denoted by
k
Ω
. This state vector is composed of the state of the
vehicle and network and thus characterized by the current node (
k
n
), the current node
arrival time (
k
t
), and
12
,
kk
kaa
s
++
∪
the congestion state of arcs
12kk
aa
+
+
∪
where
(
)
{
}
11
:
k
kk
aa ScASa
++
∈
and
(
)
{
}
22
:
k
kk
aa PScASa
++
∈
at
k
th decision stage. The
action space for the state
k
Ω
is the set of current arcs of node
k
n
,
(
)
k
CrAS n
.
At every decision stage, the trip planner evaluates the alternative arcs from
()
k
CrAS n
based on the remaining expected travel time. The expected travel time at a
given node with the selection of an outgoing arc is the expected arc travel time on the
arc chosen and the expected travel time of the next node. Let
{
}
01 1
, ,...,
K
πππ π
−
=
be
the policy of the trip and is composed of policies for each of the K-1 decision stages.
For a given state
(
)
12
,
,,
kk
kkk
kaa
nts
++
∪
Ω=
, the policy
(
)
kk
π
Ω
is a deterministic
Markov policy which chooses the outgoing arc from node
k
n
, i.e.,
(
)
(
)
kk k
aCrASn
π
Ω=∈
. Therefore the expected travel cost for a given policy vector
π
is as follows:
() ()
()
()
2
01
0
,,
k
K
kk k k K
k
FEg g
π
δ
πδ
−
−
=
⎧
⎫
Ω= Ω Ω + Ω
⎨
⎬
⎩⎭
∑
,
where
(
)
0000
,,ntSΩ=
is the starting state of the system.
k
δ
is the random travel
70

time at decision stage k, i.e.,
(
)
(
)
(
)
,,
kkkkak
tst
δδ π
≡Ω
.
(
)
(, ,)
kk k k
g
π
δ
ΩΩ
is cost
of travel on arc
()
(
)
kk k
aCrASn
π
Ω=∈
at stage
k
, i.e., if travel cost is a function (
φ
) of the travel time, then
(
)
(
)
(, ,)
kk k k k
g
π
δφδ
ΩΩ ≡
and
(
)
1K
g
−
Ω
is terminal cost
of earliness/tardiness of arrival time to the destination node under state
1K −
Ω
. Then
the minimum expected travel time can be found by minimizing
(
)
0
F
Ω
over the
policy vector
π
as follows:
(
)
{}
(
)
01 1
*
00
, ,...,
min
K
FF
πππ π
−
=
Ω
=Ω
.
The corresponding optimal policy is then
{}
(
)
01 1
*
0
, ,...,
arg min
K
F
πππ π
π
−
=
=
Ω
. Hence, the
Bellman’s cost-to-go equation for the dynamic programming model can be expressed
as follows [10]:
()
(
)
(
)
{
}
**
1
min ( , , )
kk
kkkkkk
FEg F
πδ
πδ
+
Ω= Ω Ω + Ω
.
For a given policy
()
kk
π
Ω
, we can re-express the cost-to-go function by writing
the expectation in the following explicit form:
()( )
(
)
() ()
()
()
()
()
,1 ,1
12
11 2
111
11,, ,
||,,,
|
k
ak a k
kk
kk k
kk k kk kkk
kk kk
ss
kk kaa a
Fa P aga
Ps t s t Ps t F
δ
δδ
++
++
++ +
+++
++
Ω= Ω Ω +⎡
⎣
Ω⎤
⎦
∑
∑∑
where
()
|,
kkk
P
a
δ
Ω
is the probability of travelling arc
k
a
in
k
δ
periods.
()
()
2
1
1,
k
k
ka
Ps t
+
+
+
is the long run probability of arc
(
)
22
:
k
kk
aa PScASa
++
∈
being in
state
2
1,
k
ka
s
+
+
in stage
1k +
. This probability can be calculated from the historical
frequency of a state for a given arc and time.
We use backward dynamic programming algorithm to solve for
()
*
kk
F Ω
,
1, 2, .. , 0kK K=− −
. In the backward induction, we initialize the final decision
epoch such that,
(
)
1111
,,
KKKK
nts
−−−−
Ω=
,
1K
n
−
is destination node, and
(
)
11
0
KK
F
−−
Ω=
if
1K
tT
−
≤
. Accordingly, a penalty cost is accrued whenever there is
delivery tardiness, e.g.,
1K
tT
−
>
.Note that
1K
s
−
=
∅
since destination node current
and successor arcs doesn’t have value of information.
4 Experimental Studies
In this section we first introduce two road networks for demonstrating the
performance of the proposed algorithms along with a description of their general
traffic conditions. Then describe the process of how to model recurrent congestion.
Finally, we report savings from employing the proposed model.
71
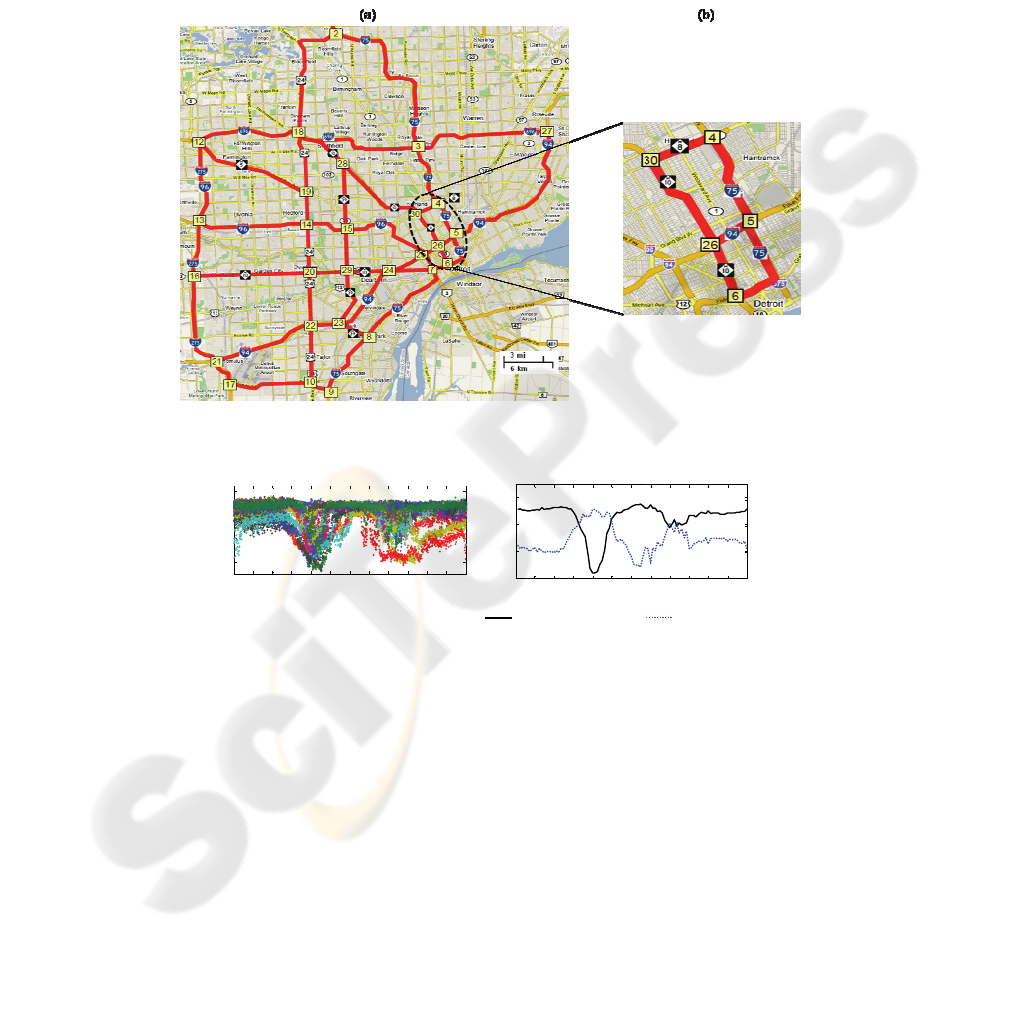
We t
e
sample
n
metro
p
ol
i
arcs and
by Michi
for the f
u
small pa
r
observed
Fig. 1. (
a
network f
r
Fig. 2. F
o
deviation
s
We
p
example.
illustrate
d
non-stati
o
Give
n
clusterin
g
arc by ti
m
method
o
4
Speed (mph)
e
st our proce
d
n
etwork cove
r
i
tan area. Th
e
55 unobserv
e
gan ITS Cent
e
u
ll 24 hours
o
r
t of our full
arcs is used
h
a
) South-East
M
r
om South-Eas
t
o
r arc 4-to-5 (
a
s
of speeds by t
h
p
resent the s
p
The mean
a
d
(Fig. 2.b).
I
o
nary distrib
u
n
the traffic s
p
g
technique t
o
m
e of day. I
n
o
f Verbeek
[
0 4am 8am
20
4
0
60
80
d
ure on a roa
d
r
s major fre
e
e
network has
e
d arcs. Real-
t
e
r for 23 wee
k
o
f each day
a
network, la
b
h
ere to better
i
M
ichigan road
t
Wayne Count
y
a
) raw traffic
s
h
e time of day
w
p
eed data for
a
nd standard
I
t can be see
n
u
tion that var
y
p
eed data, w
e
o
determine t
h
n
p
articular,
w
[
11] for its
c
12pm 4pm 8p
m
d
networ
k
fro
m
e
ways and h
i
30 nodes an
d
t
ime traffic d
a
k
days from J
a
a
t a resolutio
n
b
eled sub-net
w
i
llustrate the
m
network cons
i
y
.
s
peeds for 23
w
w
ith 15 minute
arc 4-to-5 f
o
deviations o
f
n
clearly that
t
y
with the tim
e
e
employed t
h
h
e number o
f
w
e employed
t
c
omputation
a
m
0
40
50
60
70
Mean
0
Mea
m
South-East
i
ghways in
a
d
a total of 9
8
a
ta for the ob
a
nuary 21, 20
0
n
of an obser
v
w
or
k
(Fig. 1
b
m
ethods and r
i
dered for ex
pe
w
eekdays (b)
m
time interval r
e
o
r the given
f
speed for
t
t
he traffic sp
e
e
of the day.
h
e Gaussian
M
f
recurren
t
-co
n
t
he greedy le
a
l efficiency
4am 8am 12p
m
4am 8am 12p
m
n speed (mph)
Michigan (F
i
a
nd a
r
ound t
h
8
arcs with 4
3
served arcs i
s
0
8 to Feb
r
uar
y
v
ation every
m
b
), with 5 no
d
esults.
e
rimental stud
y
m
ean (mph) a
n
e
solution.
days in Fig.
t
he arc 4-to-
5
e
eds follow a
M
ixture Mod
e
n
gestion state
a
rning GMM
and perform
a
m
4pm 8pm
m
4pm 8pm
0
5
1
1
Standard Dev
i
g. 1). The
h
e Detroit
3
observed
s
collected
y
20, 2008
m
inute. A
d
es and 6
y
. (b) Sub-
n
d standard
2.a as an
5
is also
s
t
ochastic
e
l (GMM)
s for each
clustering
a
nce. The
0
5
0
5
Std. Dev.
iation
72

parameters of the traffic state joint Gaussian distributions (i.e.,
,1 ,1
;
ii
tt tt
+
+
μΣ
) along
with the computed cut-off speeds (if GMM yields more than one state) are employed
to calculate travel time distribution parameters and the transition matrix elements as
explained in section 3. In the event that two states are identified by GMM,
ߙ
௧
denotes
the probability of state transition from congested state to congested state whereas
ߚ
௧
denotes the probability of state transition from uncongested state to uncongested state.
Fig. 3a plots these transition rates for the arc 4-to-5 with a 15 minute time interval
resolution. The mean travel time of arc 4-to-5 for congested and uncongested traffic
states are given in Fig. 3b.
Fig. 3. For arc 4-to-5 (a) recurrent congestion state-transition probabilities where α: congested
to congested transition; β: uncongested to uncongested transition probability; (b) mean travel
time for congested and uncongested traffic states.
In the experiments based on the sub-network, node 4 is considered as the origin
node and node 6 as the destination node of the trip. As stated earlier, we consider
node 4 as the origin node and node 6 as the destination node of the trip. Three
different path options exist (path 1: 4-5-6; path 2: 4-5-26-6; and path 3: 4-30-26-6).
Given the historical traffic data, path1: 4-5-6 dominates other paths most of the time
of a day under all network states. Hence we identify path 1 as the baseline path and
show the savings (averaged over 10,000 runs) from using the proposed dynamic
routing algorithm with regard to baseline path. Fig. 4a plots the corresponding
percentage savings from employing the dynamic vehicle routing policy over the
baseline path for each network traffic state combination and Fig. 4b shows the
average savings (averaged across all network traffic states, treating them equally
likely). It is clear that savings are higher and rather significant during peak traffic
times and lower when there is not much congestion, as can be expected.
Fig. 4. (a) Savings for each of 32 network state combinations and (b) average savings for all
state combinations during different times of the day.
Besides the sub-network (Fig. 1b), we have also randomly selected 4 other origin
0 4am 8am 12pm 4pm 8pm
0
0.25
0.5
0.75
1
Arc 3
Probability
0 4am 8am 12pm 4pm 8pm
2
4
6
8
Mean
α β
Congested Uncongested
0 4am 8am 12pm 4pm 8pm
0
10
20
30
(a)
Savings (%)
0 4am 8am 12pm 4pm 8pm
0
10
20
30
(b)
Savings (%)
73
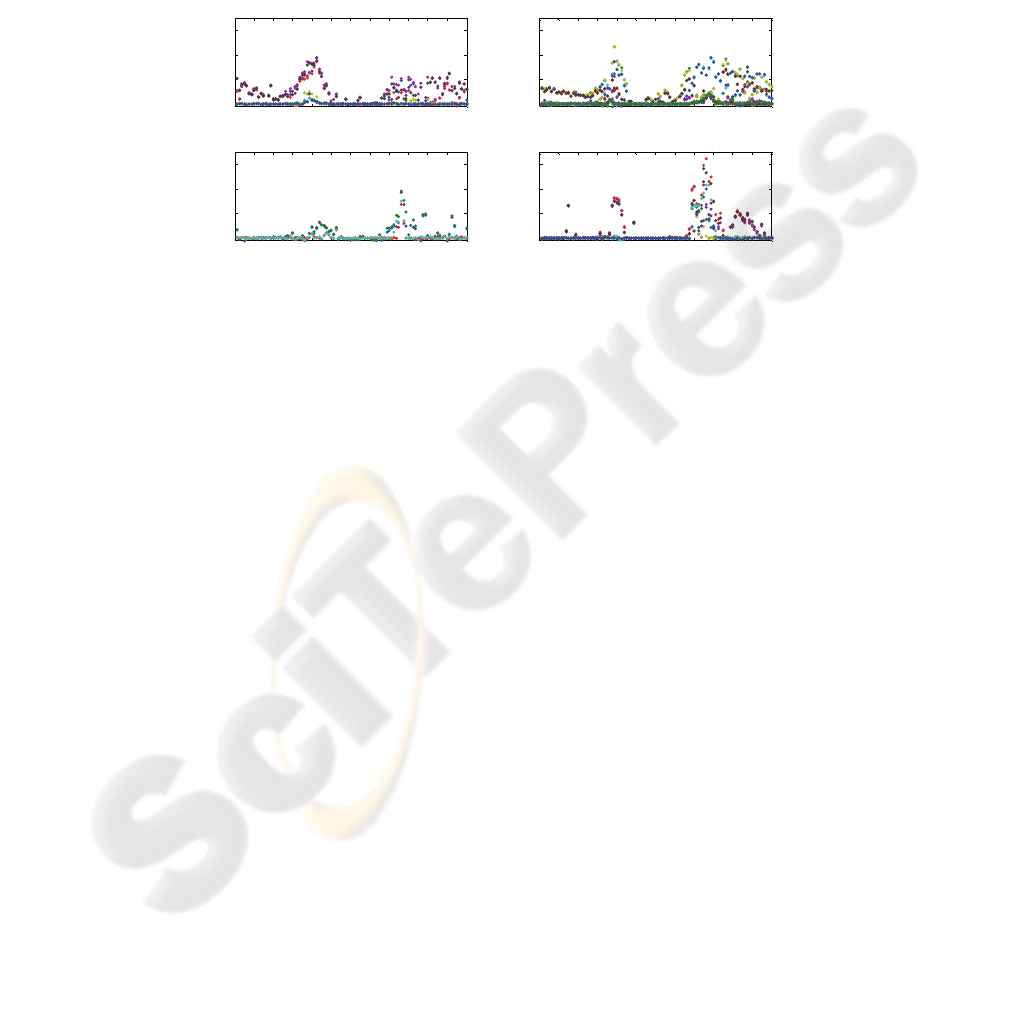
and destination (OD) pairs (OD pair 1: 2-21, 2: 12-25, 3: 19-27, and 4: 23-13) to
investigate the potential savings from using real-time traffic information under a
dynamic routing policy. Once again, we identify the baseline path for each OD pair
(as explained for the case of routing on the sub-network) and show percentage savings
in mean travel times (over 10,000 runs) over the baseline paths from using the
dynamic routing policy. The savings, Fig. 5, are consistent with results from the sub-
network, further validating the sub-network results.
Fig. 5. Savings of dynamic policy over baseline path during the day for all starting states of
given OD pairs of full network (with 15 minute time interval resolution).
5 Conclusions
The paper proposes practical dynamic routing models that can effectively exploit real-
time traffic information from ITS regarding recurrent congestion in transportation
networks. With the aid of this information and technologies, our models can help
drivers avoid or mitigate trip delays by dynamically routing the vehicle from an origin
to a destination in road networks. We model the problem as a non-stationary
stochastic shortest path problem under recurrent congestion. We propose effective
data driven methods for accurate modeling and estimation of recurrent congestion
states and their state transitions.
ITS data from South-East Michigan road network, collected in collaboration with
Michigan ITS Center, is used to illustrate the performance of the proposed models.
Experiments show that as the uncertainty (standard deviation) in the travel time
information increases, the dynamic routing policy that takes real-time traffic
information into account becomes increasingly superior to static path planning
methods. The savings however depend on the network states as well as the time of
day. The savings are higher during peak times and lower when traffic tends to be
static (especially at nights).
0 4am 8am 12pm 4pm 8pm
0
10
20
30
OD pair 1
Savings (%)
0 4am 8am 12pm 4pm 8pm
0
10
20
30
OD pair 2
Savings (%)
0 4am 8am 12pm 4pm 8pm
0
10
20
30
OD pair 3
Savings (%)
0 4am 8am 12pm 4pm 8pm
0
10
20
30
OD pair 4
Savings (%)
74

Acknowledgements
This work was supported by funds from the US Department of Transportation and the
Michigan Department of Transportation through the MIOH University Transportation
Center.
References
1. Hall, R.: The fastest path through a network with random time-dependent travel time.
Transportation Science 20 (1986) 182-188
2. Fu, L.: An adaptive routing algorithm for in vehicle route guidance systems with real-time
information. Transportation Research Part B 35B (2001) 749-765
3. Waller, S.T., Ziliaskopoulos, A.K.: On the online shortest path problem with limited arc
cost dependencies. Networks 40 (2002) 216-227
4. Miller-Hooks, E.D., Mahmassani, H.S.: Least possible time paths in stochastic, time-
varying networks. Computers & Operations Research 12 (1998) 1107-1125
5. Miller-Hooks, E.D., Mahmassani, H.S.: Least expected time paths in stochastic, time-
varying transportation networks. Transportation Science 34 (2000) 198-215
6. Gao, S., Chabini, I.: Optimal routing policy problems in stochastic time-dependent
networks. Transportation Research Part B 40B (2006) 93-122
7. Psaraftis, H.N., Tsitsiklis, J.N.: Dynamic shortest paths in acyclic networks with Markovian
arc costs. Operations Research 41 (1993) 91-101
8. Kim, S., Lewis, M.E., White III, C.C.: Optimal vehicle routing with real-time traffic
information. IEEE Transactions on Intelligent Transportation Systems 6 (2005) 178-188
9. Kim, S., Lewis, M.E., White III, C.C.: State space reduction for non-stationary stochastic
shortest path problems with real-time traffic congestion information. IEEE Transactions on
Intelligent Transportation Systems 6 (2005) 273-284
10. Bertsekas, D.P.: Dynamic Programming and Optimal Control. Athena Scientific (2001)
11. Verbeek, J.J., Vlassis, N., Kröse, B.: Efficient Greedy Learning of Gaussian Mixture
Models. Neural Computation 5 (2003) 469-485
75
