
BUCKET THEN BINARY RADIX SORT
A Novel Sorting Technique
Ossama Ismail and Ahmed M. Elhabashy
College of Engineering, Arab Academy for Sciences and Technology, Alexandria, Egypt
ossama@aast.edu, a.elhabashy@hotmail.com
Keywords:
Logarithm to the base two (log), Least Significant Bit (LSB), Most Significant Bit (MSB).
Abstract:
Sorting a sequence of numbers is an essential task that is involved in many computing algorithms and tech-
niques. In this paper a new sorting algorithm is proposed that has broken the O(n log n) limit of the most
known sorting techniques. The algorithm is designed to sort a sequence of integer numbers and may be ex-
tended to operate with decimal numbers also. The proposed algorithm offers a speed up of nearly
m+3
logn
− 1,
where n is the size of the list and m is the size of each element in the list. The time complexity of the algorithm
may be considered linear under certain constraints that should be followed in the implementation phase, while
the spatial complexity is linear too. The new algorithm was given a name of Bucket Then Binary Radix Sort
as a notation for the techniques which it uses.
1 INTRODUCTION
For long decades, the sorting problem have taken a
wide part of the research field in computer sciences
and mathematics. Sorting means to re-permutate a list
to put its elements in a certain desired order. Many
sorting algorithms have been evolved to enhance the
time and memory complexities of the sorting pro-
cess. Many of the most known sorting algorithms are
known as comparison sorting. The name was choos-
ing as the sorting in these algorithms is done by com-
paring the list’ elements. The time and space com-
plexities here depend mainly on the size of the list
(n) to be sorted, and up to now, their time complexity
is bounded to O(n log n), while the space complex-
ity is constant in most of them. The most popular
and widely used algorithms of this kind are quick sort
and merge sort. While some other comparison sort-
ing algorithms such as bubble sort and insertion sort
are much less used according to the very high time
complexity of O(n
2
) compared with other algorithms.
Another kind of sorting algorithms is non compari-
son algorithms. The sorting techniques of this kind
depends mainly on the categorizing the elements of
the list instead of comparing them. The complexity
of this kind depends not only on the size of the list but
also on the size of the elements itself. Some of the
most used algorithms of this category are pigeonhole
sort, counting sort, Bucket sort and radix sort. The
new proposed sorting algorithm is a combination be-
tween some non-comparison sorting algorithms such
as counting sort, bucket sort and radix sort.
2 BUCKET THEN BINARY
RADIX SORT
Bucket Then Binary Radix Sort is a sorting technique
that will be very useful for sorting large sequences of
numbers. It works mainly with integer numbers but
could be extended to handle long, or floating num-
bers. The algorithm works on two phases. The first
phase is a combination between counting sort and
bucket sort, while the second phase is a special kind
of radix sort.
Let’s assume the following definitions:
n is the length of the array to be sorted.
m is the number of bits in the binary representation of
the largest element in the array.
k is the number of most significant bits (MSBs) used
in the first phase of the algorithm.
2.1 Algorithm Description
As mentioned before the algorithm composes of two
phases. The first phase is an enhancement of the
counting sort technique. The purpose of the first
phase is to split the sequence into a number of frag-
ments that is relatively sorted to each other, while the
elements of each fragment isn’t yet sorted. The sec-
ond phase uses a simple but efficient technique to sort
these fragments based on the binary representation of
the fragments’ elements.
2.1.1 Phase One, Bucket Sort
The functionality of this phase is to generate a num-
ber of sequences from the original sequence such that
for any two sequences Si and Sj, any element in Si is
less than all element of Sj, when ever i is less than j.
Let’s consider an array of unsigned integer. Standared
integer numbers are 32 bits. In this level we will sort
these elements based on the first k MSBs without any
consideration of the remainding bits. The process of
choosing the value of k will be discussed later when
analyzing the time complexity of the algorithm. This
level of sorting could be easily performed in linear
time by using some sort of counting sort keeping in
mind that the number of MSBs involved in this pro-
cess should be kept withen a reasonable range to allow
the counting sort to operate in a linear time and space
complexities.(Thomas H. Cormen and Stein, 2001)
This stage of sorting could be formulated with the
following terms, assuming ascending sorting is re-
quired:
• Generate an array of size 2
k
and initialize all its el-
ements to zero. This array will act as the counter
array in the counting sort technique. The counter
array used here will differ slightly from the clas-
sical counter array. An element at the index q in
a classical counter array will hold the number of
elements in the sequence to be sorted having the
value q, while an element at index q in the counter
array that is used here will hold the number of ele-
ments in the sequence having the k (MSBs) equal
to the binary representation of the value q. This
step costs constant time.
• To fill the counter array, loop over every element
in the array. Using bit masking obtain the value
of the k MSBs in each element and increment the
corresponding item in the counter array by one.
This step consumes linear time proportional to the
size of the list to be sorted.
• Based on the resulting counter array. Partion the
original sequence into virtual fragments. This step
could predict the number of the resulting frag-
ments, the size of each fragment, and the correct
starting and ending position of these fragments in
the final sorted list. This step could be performed
in exponential time complexity proportional to the
value which is chosen for k. This reflects the crit-
ical operation of choosing the value of k to keep
the complexity of this step linear compared to the
size of the original sequence.
• Based upon the resulting information that is ob-
tained from the previous step, loop on every ele-
ment in the list and insert it into the proper posi-
tion in a new list, so that the resulting list will be
composed of some virtual portions that are sorted
relatively to each other but having their elements
unsorted yet as stated before. Again the time com-
plexity of this step is linear proportional to the size
of the original list.
The cost of this phase is 2n+2
k
considering the time
and n+2
k
considering the memory. Choosing the
proper value for k keeps the time and spatial com-
plexities of this phase linear compared to the size of
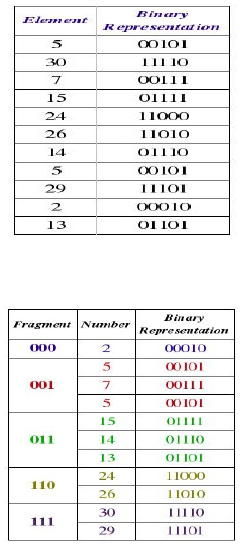
the original list as discussed later. Figure one and two
give an example of applying phase one of the algo-
rithm on an array with integer elements. In this ex-
ample n= 11 , m = 5 and k = 3. (Mahmoud and Al-
Ghreimil, 2006; Akl, 1990)
Figure 1: Unsorted list.
Figure 2: Fragments resulting from phase 1.
2.1.2 Phase Two, Binary based Sort
The second phase of the algorithm is to sort the virtual
portions that construct the list resulting from phase
one. Here some sort of radix sort is used. Instead of
considering the size of the list only, this stage of sort-
ing takes into consideration the binary representation

of the list elements along with the size of the list it-
self. Up till now we have sort the sequence according
to the k MSBs of its elements. Now our job is to in-
crease the accuracy of sorting by looking deeper to
the bits that were excluded from consideration in the
first phase.
Lets’ consider an array that contain unsorted un-
signed integer numbers and it is required to be sorted
ascending. This array could be divided into two rela-
tively sorted arrays by checking only the MSB of each
element in the array. Using the same concept the ar-
ray could be sorted completely by performing n*m
iterations, recall again the definition of n and m. The
method to do such sorting are as follow:
• Create an empty array of the same size as the orig-
inal one as well as two counters.
• Initialize the first counter to one and the second
counter to the size of the original array.
• Loop over every element in the original array and
check the value of the MSB in this element. If it
is ’0’, then insert this element into the new array
at the position in the first counter, then increment
this counter by one. If the value of this bit is ’1’,
then insert this element into the new array at the
position in the second counter, Then decrement
this counter by one. Now the new array is com-
posed of two parts. All the elements in first part
have the MSB equal to ’0’, while all the elements
of the second part have the MSB equal to ’1’.
• Consider every part which were generated in the
previous step an array itself, and apply on each of
them the same procedure. But instead of checking
the MSB, the second most significant bit should
be checked.
• Again consider every part of the four parts that are
generated in the previous step an array and apply
the same procedure and check the third MSB.
• Continue performing this procedure until the least
significant bit (LSB) is checked.
Note that in the implementation phase the previ-
ous procedure could be done using only one extra ar-
ray of the same size as the original one. The por-
tions that are generated after each iteration could be
an imaginary portions located into one of the two ar-
rays that are used. It is worth saying that this pro-
cedure could be done in an iterative manner or a re-
cursive manner. The iterative implementation will be
more efficient when considering the time but less ef-
ficient when considering the memory as it will use a
third array to carry the starting and ending positions
of the resulting fragments. While the recursive imple-
mentation will use less memory but will suffer from
the overhead of recursively calling the sorting func-
tion. Figure 3 and 4 illustrate an example of this pro-
cedure.
Figure 3: Phase two (Decimal Values).
Figure 4: Phase two (Binary Values)
Now let’s recall again that the result of phase one
is an array consisting of a number of consecutive parts
which are relatively sorted to each other but still there
elements are not sorted. clearly we could continue
sorting these parts using the procedure that was illus-
trated above with the first bit that is to be checked
is the first MSB immediately after the k MSBs used
in phase one and continuing until the least significant
bit (LSB) is reached. Therefore this phase will check
only the (m-k) least significant bits that were excluded
in phase one. Accordingly this phase will exhausts
n*(m-k) iterations.(Black, 2009; P. M. McIlroy and
McIlroy, 1993)
2.2 Time Complexity Analysis
Phase one of the algorithm has a time complexity of
O(2n+2
k
), while phase two has a time complexity of

O(n*(m-k)). Therefore the overall complexity of the
algorithm will be O(n(m-k+2) + 2
k
). Note that we
preserve the constant terms in the complexity equa-
tion as it will be critical in large sets of data.
In order to keep the time complexity linear, the
following condition must occure,
2
k
<= C*n. or k <= C log n
where C is any constant
again, in order to minimize the total complexity,
the first differentiation of the complexity equation
should be performed.
d
dk
[(m − k + 2)n + 2
k
] = 0 (1)
−n + 2
k
= 0 (2)
2
k
= n (3)
k = log(n) (4)
So the theoretical minimum time complexity is
O(n(m+3-log n)).
Figure (5) shows an example curve for choosing the
optimum value of k. In this example m=32, n=10
7
.
Figure 5: k optimum value.
Note that the actual complexity would be mul-
tiplied by a certain constant due to the implemen-
tation itself. In other words, the complexity gives
the number of iterations, while in the implementa-
tion phase every iteration consumes a processing time
itself. Therefore the actual enhancement offered by
this algorithm couldn’t be reached yet, but it may be
reached by trying different implementation methods.
As long as the time complexity of the most known
efficient sorting algorithms is O(n log(n)), so in order
for the new algorithm to be more efficient,
n(m + 3 − log(n)) <= n ∗ log(n) (5)
m + 3 − log(n) <= log(n) (6)
m + 3 <= 2 ∗ log(n) (7)
m <= 2 ∗ log(n) − 3 (8)
In other words the new algorithm should be more ef-
ficient when m <= 2 log n -3.
Figure (6) shows a theoretical comparison between
the time complexity of the proposed algorithm
,O(n(m+3-log n)), and one of the algorithms which
operates in O( n log n) when sorting a list of unsigned
32 bits integer values.
Figure (7) shows a real time comparison between the
proposed algorithm and the quick sort technique when
sorting an array of unsigned 32 bits integers. The new
algorithm was implemented using C language, while
the quick sort results were obtained using the pre-
made C function “qsort“. This comparison was per-
formed under an apple machine running OS X 10.5.6
with the following specs: 2.66 GHz processor sup-
ported with a 6 MB L2 cache and 4.0 GB of RAM.
(Thomas H. Cormen and Stein, 2001; Skiena and Re-
villa, 2003)
Figure 6: n log n Vs. Bucket then Binary Radix.
2.3 Memory Complexity
Phase one of the algorithm has a spatial complexity of
O(2
k
+n) besides the actual n spaces reserved for the
original array. The iterative implementation of phase
two will consume another n spaces besides the mem-
ory reserved in the first phase. Accordingly the to-
tal memory usage of the iterative implementation of
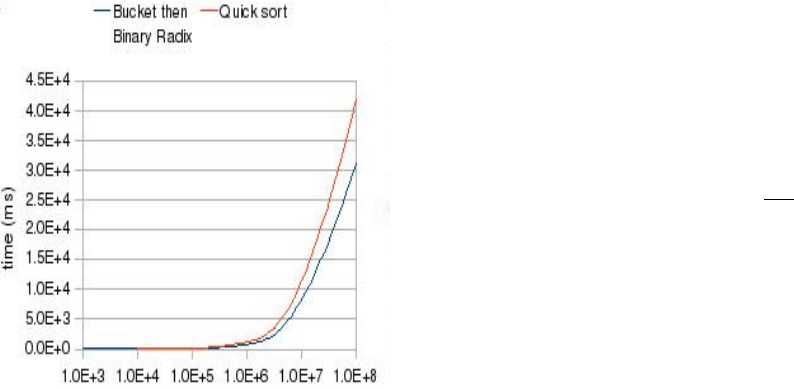
Figure 7: Bucket then Binary Radix Vs. Quick Sort.
the algorithm will be 3n+2
k
. Recalling from the time
complexity analysis that k should be equal to log n,
will rephrase the memory usage to O(4n), which is
clearly linear complexity. Again the constants aren’t
neglected for there critical effect in large sets of data.
2.4 General Characteristics
• Stability: The proposed algorithm isn’t consid-
ered to be stable as it doesn’t maintain the relative
order of records with equal keys.
• In-place: The algorithm isn’t an in-place sorting
algorithm. It doesn’t depends on swapping the list
elements. Indeed it consumes linear space not a
constant one.
• Time complexity: The time complexity of the pro-
posed sorting algorithm is O(n(m+3-log n)). Re-
call that n is the size of the list and m is the number
of bits in the list’s elements.
• Memory Usage: as mentioned before, the algo-
rithms consumes linear memory space equals to
4n.
• Recursion: Phase two of the algorithm may be
implemented recursively with the risk of reducing
the time enhancement dramatically.
• Comparison sorting: The algorithm is not a com-
parison sorting algorithm. It depend on rebuilding
the list instead of reordering it by comparing its
elements.
• Adaptability: The initial sort degree of the list
doesn’t affect the algorithm’s time or spacial com-
plexties. Therefore, it is an adaptive sorting algo-
rithm.
3 CONCLUSIONS
A new sorting algorithm was proposed that will be
efficient in sorting large sets of data. The data associ-
ated with the new algorithm is preferred to be integer
values with limited size of bits, but it may be reconfig-
ured to work with other types of data such as decimal
numbers. The run time of the algorithm is O(n(m+3-
log n)) which reflects a speed up of
m+3
logn
− 1 com-
pared to the most known efficient sorting algorithms.
The memory usage is linear proportional to the size of
the list. The actual speed up obtained from the algo-
rithm was about 50 percent of the theoretical offered
enhancement. This is due to the implementation com-
plexity of the algorithm specially the first phase of its
two phases.
REFERENCES
Akl, S. G. (1990). Parallel Sorting Algorithms. Academic
Press, Inc., Orlando, FL, USA.
Black, P. E. (April 2, 2009). Dictionary of Al-
gorithms and Data Structures. U.S. Na-
tional Institute of Standards and Technology,
http://www.itl.nist.gov/div897/sqg/dads/.
Mahmoud, H. A.-H. and Al-Ghreimil, N. (2006). A novel
in-place sorting algorithm with o(n log z) compar-
isons and o(n log z) moves. In Proceedings of World
Academy of Science, Engineering and Technology
Volume 16 November 2006 ISSN 1307-6884. WASET.
P. M. McIlroy, K. B. and McIlroy, M. D. (1993). Engineer-
ing radix sort. In Computing Systems 6 (1993) 5-27.
Skiena, S. S. and Revilla, M. (2003). Programming Chal-
lenges: The Programming Contest Training Manual.
Springer-Verlag New York, Inc., Secaucus, NJ, USA.
Thomas H. Cormen, Charles E. Leiserson, R. L. R. and
Stein, C. (2001). Introduction to Algorithms. MIT
Press and McGraw-Hill, 2nd edition.
