A Model of an Interregional Logistic System

for the Statement and Solution

of Decision Problems at the Operational Level

Chiara Bersani, Davide Giglio, Riccardo Minciardi, Michela Robba

Roberto Sacile, Simona Sacone and Silvia Siri

Department of Communications, Computer and Systems Science

University of Genova, Via Opera Pia 13, 16145 Genova, Italy

Abstract. A regional/multi-regional logistic trafﬁc network is considered in this

paper with the aim of optimizing the ﬂows of goods which pass through the net-

work in order to reach their ﬁnal destinations. The logistic network takes into

account both road and rail transportation, and it is modelled as a directed graph

whose arcs represent a road or a rail link and whose nodes are not only connec-

tion points but can represent a place where some service activities (such as the

change in transportation mode) are carried out. In the paper, the model of the

logistic network and, in particular, the equations which formalize the dynamics

of links and nodes, are described in detail. In addition, with reference to decision

problems at operational level, some considerations about the degrees of freedom

(decision variables) in the model, the kind and the role of decision makers, and

the class of performance indicators are also outlined in the paper.

1 Introduction

Modelling, planning, and control of logistic systems are research streams that, in the

last years, have received a signiﬁcant attention by the research community due to their

economic impact. An improvement of the performance of the overall logistic chain

and an effective integration of the different actors of a logistic system are fundamental

goals in the management of modern production/distribution systems. As a matter of

fact, these systems have to be designed and planned to fulﬁl such relevant objectives as

those related to the on-time delivery of products to ﬁnal users, to the minimization of

transportation costs and of costs referred to the use of infrastructures, etc.

In this context, off-line planning methodologies play a key role and a wide bibli-

ography can be found on such subjects. Some interesting review works [1–4] deﬁne

the hierarchical decisional structure to be used when dealing with systems devoted

to freight intermodal transportation and, then, with logistic systems. This structure is

composed of three levels: long term (or strategic) planning, medium term (or tactical)

planning, and short term (or operational) planning. At the strategic level, planning prob-

lems are mainly relevant to demand forecasting, logistic nodes location [5,6] and to the

design of transportation operations between nodes [7,8]. The tactical level consists in

Bersani C., Giglio D., Minciardi R., Robba M., Sacile R., Sacone S. and Siri S. (2009).

A Model of an Interregional Logistic System for the Statement and Solution of Decision Problems at the Operational Level.

In Proceedings of the 3rd International Workshop on Intelligent Vehicle Controls & Intelligent Transportation Systems, pages 76-85

 SciTePress

the aggregate planning of operations in logistic nodes [9] and of distribution operations

(Service Network Design problems [10]). Many decision problems are typically deﬁned

at the operational level and such problems require the adoption of several models and

decision techniques; typical decision problems at this level are the assignment of trans-

portation operations to transportation means [11] and the static and dynamic routing of

vehicles on the transportation network or on the logistic chain [12,13]. The model and

the problems considered in this paper refer to this latter decision level.

In this paper, the model of a logistic trafﬁc network at regional/multi-regional level

is presented, being the ﬁnal objective of the current research activity the statement and

solution of decision problems for the management of a logistic system at operational

level, such as the optimal routing of goods which pass through the logistic network

in order to reach their ﬁnal destinations. The proposed model is a discrete-time model

and the time horizon to be considered can range from some hours to some days. The

model mainly consists of a directed graph whose arcs represent a road or a rail link

and whose nodes are not only connection points but can represent a place where some

service activities (such as the change in transportation mode) are carried out. The model

is based on some characteristics which have been introduced in [14] with reference to

the macroscopic modelling of transportation networks. In particular, each link and some

nodes of the logistic network are discrete-time dynamic systems whose input and output

variables are represented by ﬂows that are respectively received from and transmitted

to the neighbouring links/nodes, and the basic dynamic equation is represented by the

vehicle conservation equation introduced in [15,16]. In addition, with reference to de-

cision problems at operational level, some considerations about the degrees of freedom

(decision variables) in the model, the kind and the role of decision makers, and the class

of performance indicators are also outlined in the conclusions of the paper.

2 The Model of the Logistic Network

The model of the logistic network mainly consists of the transportation offer (i.e., the

physical network where vehicles can move), the transportation demand (i.e., the re-

quirements of moving goods over this network) and the equations that represent the

dynamics of this system, both referred to nodes and links. The model is a discrete-time

model; in this connection, let t and ∆ be the generic time instant and the length of one

interval, respectively, with t = 0, . . . , T being T ∆ the time horizon. Note that, for the

quantities considered in the model which are not referred to a time instant but to a time

interval, with t we refer to the time interval [t, t + 1).

2.1 The Transportation Offer

The offer of transportation services is represented by means of a directed graph D =

(V, A) where V is the set of nodes and A is the set of links. We will refer to each node

as i ∈ V and to each link as the pair of nodes it connects, i.e. (i, j) ∈ A. For each node

i ∈ V the sets P(i) and S(i) gather the predecessor and successor nodes, respectively.

The graph D represents an intermodal network involving two transportation modes

corresponding to road and rail. Let us denote with A

and A

the set of arcs on road

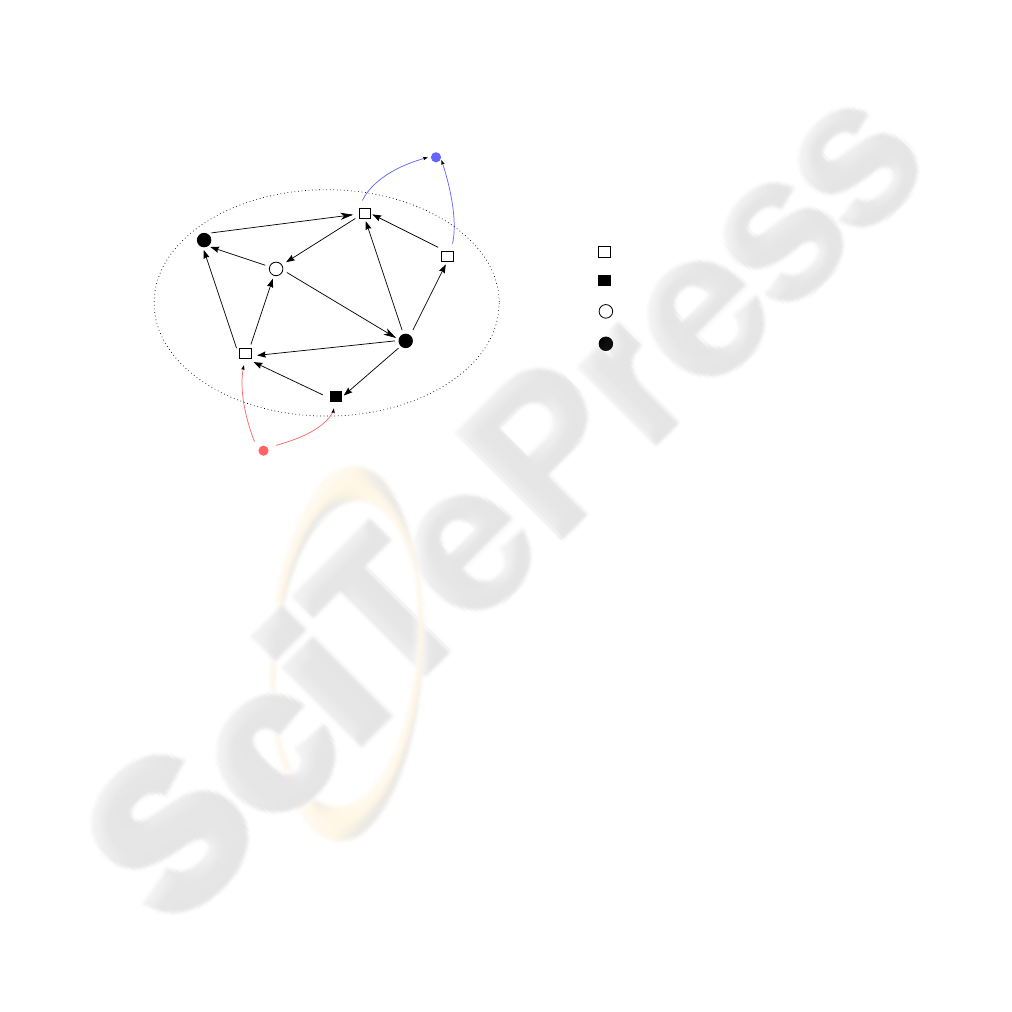
and on rail, respectively. It is A

∩ A

= ∅ since an arc corresponds univocally to a

given transportation mode. Moreover, it is obvious that A

∪ A

= A.

The nodes of the network are primarily divided into connection nodes and service

nodes. The former are simply interconnections among different links and do not have

their own dynamics, whereas the latter represent a place where some service activi-

ties are carried out (such as intermodal terminals where cargo is handled and there

is a change in the transportation mode) and then are modelled as discrete-time dy-

namic systems. Both connection and service nodes can be either regular nodes or bor-

der nodes. Border nodes represent the access and exit points of the network. In this

connection let V

, V

, and V

be, respectively, the set of regular connection,

border connection, regular service, and border service nodes. These sets are disjoint

∩ V

= ∅) and their union correspond to the whole set of nodes

∪ V

= V).

D = (V, A)

o ∈ Ω

d ∈ Ω

Border Connection node

Border Service node

Regular Connection node

Regular Service node

Fig.1. A sketch of the logistic network.

2.2 The Transportation Demand

In the considered model, we suppose that the real origins and destinations of the demand

are outside the transportation network D. However, all goods must pass through the

proposed regional/multi-regional logistic trafﬁc network in order to reach their ﬁnal

destinations. At this purpose, let Ω

and Ω

represent, respectively, the set of origins

and the set of destinations for the whole demand (see Fig. 1). Note that there can be

some geographic areas that are both the origin and the destination of logistic ﬂows, then

in general Ω

∩ Ω

6= ∅. Goods coming from a certain origin may enter the network

through one or more “compatible” border nodes; in the same way goods can reach their

destination by exiting the network from one or more “compatible” border nodes. Then,

let V

⊆ V

∪ V

(resp., V

OUT

⊆ V

∪ V

) be the set of border nodes associated

with origin o ∈ Ω

(resp., destination d ∈ Ω

). Moreover, for each destination d ∈ Ω

and for each node µ ∈ V

OUT

, we denote with τ

µ,d

(t) the time necessary to reach d from

µ if the logistic units are in µ at time t.

The transportation demand is deﬁned for each different network user, i.e., road car-

rier, shipper and so on, that needs to transport some logistic units from a certain origin

to a certain destination. Each network user is denoted with n = 1, . . . , N and it has a

set of Γ

transportation requests to satisfy. The l-th request of user n, n = 1, . . . , N,

l = 1, . . . , Γ

, is characterized by: origin o

n,l

∈ Ω

, destination d

n,l

∈ Ω

, number

of logistic units δ

n,l

, due date dd

n,l

, release time rt

n,l

, i.e., the time instant in which

the logistic units are available to enter the network. In addition, let st

n,l

be the time

instant in which the logistic units actually enter the network; moreover, λ

ν,µ

n,l

, ν ∈ V

n,l

µ ∈ V

OUT

n,l

represents the percentage of δ

n,l

that enter the network in ν and exit from

µ. Note that these last two terms are decision variables whose values depend on the

choices taken by the network user.

Finally, in order to associate the request l of network user n with the considered

time horizon, let the function of time δ

n,l

(t) be deﬁned as follows:

n,l

(t) =



n,l

if t = st

n,l

0 otherwise

n = 1, . . . , N l = 1, . . . , Γ

t = 0, . . . , T (1)

3 The Dynamics of the Logistic Network

Links and nodes are considered as discrete-time dynamic systems whose state is rep-

resented by the number of logistic units which are in the link or node at a certain time

instant. Each state variable is updated according to a state equation (conservation equa-

tion) which takes into account the number of logistic units entering and exiting the

link or node in the time interval between two subsequent time instants. Moreover, in

order to separately consider all requests of all network users and all exiting nodes, an

approach similar to the one proposed in [14], which considers destination-oriented vari-

ables (composition and splitting rates), is adopted.

3.1 Links

The dynamics of links involves road links only, since trains transporting a ﬁnite number

of logistic units over a rail link are not explicitly modelled. As it will be clear in the

following, the dynamics of trains is implicitly considered in the dynamics of service

nodes. Then, in the following, it is assumed (i, j) ∈ A

Let us denote with n

n,l,µ

i,j

(t), n = 1, . . . , N, l = 1, . . . , Γ

, µ ∈ V

OUT

n,l

, t = 0, . . . , T ,

the number of logistic units, belonging to the l-th transportation request of network user

n, which are in link (i, j), at time t, and have to reach border node µ. In the following,

the triple (n, l, µ) will be referred to as a whole. The state equation is then given by:

n,l,µ

i,j

(t + 1) = n

n,l,µ

i,j

(t) + q

n,l,µ

i,j

(t) − Q

n,l,µ

i,j

(t) (2)

where q

n,l,µ

i,j

(t) and Q

n,l,µ

i,j

(t) are, respectively, the number of logistic units of (n, l, µ)

which enter and exit (i, j) in the time interval [t, t + 1).

n,l,µ

i,j

(t) is given by:

n,l,µ

i,j

(t) = γ

n,l,µ

i,j

(t) · Q

i,j

(t) (3)

being the overall number of logistic units exiting from (i, j), namely Q

i,j

(t), obtained

from

i,j

(t) = v

i,j

(t) · ρ

i,j

(t) · ∆ (4)

where v

i,j

(t) and ρ

i,j

(t) indicate the mean speed and the density on link (i, j) in the

time interval [t, t + 1). If we suppose that the density is uniformly distributed along

(i, j) and constant in [t, t + 1), we can deﬁne the density as:

i,j

(t) =

i,j

(t) + m

i,j

(t)

i,j

(5)

where L

i,j

is the length of (i, j) and m

i,j

(t) represents the number of other vehicles

(such as cars or other logistic vehicles which are not matter of decision in the considered

system) present in (i, j) at time t. The value of m

i,j

(t) is supposed to be known, at

least as an average value, and then it is an input to the problem. However, note that

i,j

(t) must be taken into account because it affects the trafﬁc behaviour and, then, the

evolution of the state variable.

Moreover, the mean speed on the link is deﬁned as v

i,j

(t) = f[ρ

i,j

(t), (i, j), t],

i.e., it is a function of the density on the link (as well as function of the link itself and

of the time instant). This relation is generally known as the steady state speed-density

characteristic [17].

The link composition rate γ

n,l,µ

i,j

(t) speciﬁes the fraction of logistic units, which

are actually in link (i, j), belonging to (n, l, µ), with respect of the overall number of

logistics units in (i, j). It is computed as

n,l,µ

i,j

(t) =

n,l,µ

i,j

(t)

i,j

(t)

n,l,µ

i,j

(t)

n=1

l=1

µ∈V

OUT

n,l

n,l,µ

i,j

(t)

(6)

The equation providing q

n,l,µ

i,j

(t) depends on the kind of node i. If node i is a regular

connection node, then

n,l,µ

i,j

(t) =

h∈P(i)

n,l,µ

h,i,j

(t) · Q

h,i

(t) i ∈ V

(7)

where β

n,l,µ

h,i,j

(t) is the link splitting rate from link (h, i) to link (i , j), in the time interval

[t, t + 1), with reference to (n, l, µ). The link splitting rates are given by

n,l,µ

h,i,j

(t) = γ

n,l,µ

i,j

(t) · α

n,l,µ

h,i,j

(t) (8)

where α

n,l,µ

h,i,j

(t) are route choice parameters. If node i is a border connection node and

represents one of the access points for the logistic units belonging to (n, l, µ) (that is,

i ∈ V

n,l

), then

n,l,µ

i,j

(t) = β

n,l,µ

i,j

(t) · λ

i,µ

n,l

· δ

n,l

(t) i ∈ V

n,l

⊆ V

(9)

where β

n,l,µ

i,j

(t) is the node splitting rate from node i to link (i, j), in the time interval

[t, t + 1), with reference to (n, l, µ). Finally, if node i is a service node, both regular

and border, the dynamics of the node must be taken into account, thus

n,l,µ

i,j

(t) = β

n,l,µ

i,j

(t) ·

(t) i ∈ V

∪ V

(10)

where

(t) is the number of logistic units exiting the node i (see next subsection).

3.2 Nodes

The dynamics of nodes is related to the possibility of queuing logistic units inside the

node and thus it involves service nodes only (both regular and border). Let us denote

with n

n,l,µ

(t), n = 1, . . . , N, l = 1, . . . , Γ

, µ ∈ V

OUT

n,l

, t = 0, . . . , T , the number of

logistic units, belonging to the l-th transportation request of network user n, which are

in node i, at time t, and have to reach border node µ. As before, in the following, the

triple (n, l, µ) will be referred to as a whole. The state equation is then given by:

n,l,µ

(t + 1) = n

n,l,µ

(t) + q

n,l,µ

(t) − Q

n,l,µ

(t) (11)

where q

n,l,µ

(t) and Q

n,l,µ

(t) are, respectively, the number of logistic units of (n, l, µ)

which enter and exit i in the time interval [t, t + 1).

n,l,µ

(t) is given by

n,l,µ

(t) =

n,l,µ

(t) +

n,l,µ

(t) (12)

where

n,l,µ

(t) (resp.,

n,l,µ

(t)) represents the overall number of logistic units, be-

longing to (n, l, µ), exiting from node i and entering a road link (resp., rail link).

n,l,µ

(t) is provided by

n,l,µ

(t) = eγ

n,l,µ

(t) ·

(t) (13)

where eγ

n,l,µ

(t) is the node-to-road composition rate, and

(t) is the overall number

of logistic units exiting i and entering a road link; this last term is given by

(t) = min



eσ

(t) · n

(t), es

(t) · ∆



(14)

with

eσ

(t) =

n=1

l=1

µ∈V

OUT

n,l

eσ

n,l,µ

(t) (15)

being eσ

n,l,µ

(t) the fraction of logistic units of (n, l, µ) which are in node i at time t and

leave, in the subsequent time interval, namely [t, t + 1), the node towards a road link or

leave the network, and

(t) =

n=1

l=1

µ∈V

OUT

n,l

n,l,µ

(t) (16)

Then, the node-to-road composition rate can be computed as

eγ

n,l,µ

(t) =

eσ

n,l,µ

(t) · n

n,l,µ

(t)

eσ

(t) · n

(t)

(17)

In (14), es

(t) represents the node-to-road service rate (expressed as number of logistic

units per time unit) in the node i in the time interval [t, t + 1). Note that it is assumed

that every logistic unit entering a service node in a given time interval cannot exit the

node itself in the same time interval.

Before introducing the equation providing

n,l,µ

(t), it is necessary to brieﬂy de-

scribe the behaviour of logistic units on rail links. A rail link (i, j) ∈ A

is assumed to

be served by one or more trains which transport logistic units from i to j. It is assumed

that one train begins a transportation in i at each time instant and the number of logistic

units that are transported by the train depends on the state of the node. However, such a

number is upper-bounded by a value C

i,j

(t) which represents the capacity (maximum

number of logistic units that can be transported) of the train leaving i towards j, at time

instant t. Moreover, let Λ

i,j

be the travel time of a train travelling from i to j, expressed

as number of time intervals; such a value is assumed ﬁxed and a-priori known.

Because of the ﬁnite capacity of trains, some of the logistic units that concluded

their service and that have to proceed with their travel in a rail link, may be not allowed

to exit the node. Then, it is necessary to distinguish between the “potential” number of

logistic units which leave from the node and the “actual” number. In (12),

n,l,µ

(t), is

the actual number. The potential number is provided by

POT n,l,µ

(t) = bγ

n,l,µ

(t) ·

POT

(t) (18)

where bγ

n,l,µ

(t) is the node-to-rail composition rate, and

POT

(t) is the overall number

of logistic units which potentially exit i and enter a rail link; this last term is given by

POT

(t) = min



bσ

(t) · n

(t), bs

(t) · ∆



(19)

with

bσ

(t) =

n=1

l=1

µ∈V

OUT

n,l

bσ

n,l,µ

(t) (20)

being bσ

n,l,µ

(t) = 1 − eσ

n,l,µ

(t), ∀(n, l, µ), the fraction of logistic units of (n, l, µ)

which are in node i at time t and leave the node towards a rail link. Then, the node-to-

rail composition rate can be computed as

bγ

n,l,µ

(t) =

bσ

n,l,µ

(t) · n

n,l,µ

(t)

bσ

(t) · n

(t)

(21)

In (19), bs

(t) represents the node-to-rail service rate in the node i in the time interval

[t, t+1). The actual number of logistic units which leave from the node is then computed

n,l,µ

(t) =

j∈S(i)

(i,j)∈A

n,l,µ

i,j

(t) ·

POT n,l,µ

(t) (22)

where

n,l,µ

i,j

(t) represents the fraction of logistic units of (n, l, µ) which actually leave

the node i towards rail link (i, j), with respect to the relative potential number. It is

worth noting that the meaning of

n,l,µ

i,j

(t) is different from that of splitting rates in-

troduced in the link dynamics. Moreover, such quantities must satisfy the following

constraint

n=1

l=1

µ∈V

OUT

n,l

n,l,µ

i,j

(t) ·

POT n,l,µ

(t) ≤ C

i,j

(t) (23)

It is worth ﬁnally observing that, when i = µ, all logistic units belonging to (n, l, µ)

leave the network; in this case, it turns out eσ

n,l,µ

(t) = 1, bσ

n,l,µ

(t) = 0, t = 0, . . . , T .

Coming back to (11), q

n,l,µ

(t) is given by

n,l,µ

(t) =

(

i,µ

n,l

· δ

n,l

(t) i ∈ V

n,l

⊆ V

n,l,µ

(t) + bq

n,l,µ

(t) i ∈ V

∪ V

, i /∈ V

n,l

⊆ V

(24)

where, in case of service nodes that are not an access point for logistic units belonging

to (n, l, µ) (bottom expression of (24)), eq

n,l,µ

(t) (resp., bq

n,l,µ

(t)) represents the overall

number of logistic units, belonging to (n, l, µ), coming from a road link (resp., rail link)

and entering node i. eq

n,l,µ

(t) and bq

n,l,µ

(t) are provided by

n,l,µ

(t) =

h∈P(i)

(h,i)∈A

n,l,µ

h,i

(t) (25)

n,l,µ

(t) =

h∈P(i)

(h,i)∈A

n,l,µ

h,i

(t − Λ

i,j

) ·

POT n,l,µ

(t − Λ

i,j

) (26)

4 Conclusions and Further Research Directions

In the previous section the model of an intermodal logistic network has been presented.

The dynamic evolution of the elements (links and nodes) of this network has been rep-

resented by means of discrete-time state equations where the state variables indicate the

number of logistic units present in a link or in a node. The main decisions to be taken

concern the splitting of these logistic units over the alternative paths in the network (and

consequently the choice of transportation mode) and the time instant in which they enter

the network. Different approaches can be deﬁned in order to determine these decisions

and they depend on which decision makers are considered and, for each decision maker,

the decision power, the available information and the performance indexes.

Three classes of decision makers can be considered in general. First of all, network

users are decision makers that must move goods from given origins to given destina-

tions, characterized by speciﬁc due dates. These network users work in a competitive

environment, therefore each of them is characterized by a speciﬁc objective (i.e. mini-

mizing costs and/or travel times in order to deliver goods within a given due date). An-

other class of decision makers is given by infrastructure managers, such as managers

of links (e.g. highways) or managers of nodes (e.g. terminal operators) or managers of

trains. Each of them has, again, a speciﬁc objective (i.e. minimizing risk factors, max-

imizing proﬁts, and so on) that can be in conﬂict with the objectives of other decision

makers. A third class of decision makers is represented by the local authorities or terri-

tory managers devoted to manage the territory with social objectives (such as assuring

security, minimizing trafﬁc congestion, and so on). These three classes of decision mak-

ers are involved in a decision framework that is, in general, a hierarchic structure. The

territory manager is at the top of this decision structure, it decides on the basis of its

social objectives and it can act on the system in two ways, by advising the other deci-

sion makers about how to act or by imposing to them some policies (e.g. forbidding to

cover a given link in a certain time period, imposing the number of speciﬁc cargo units

that can move in a part of the network, and so on). The decisions taken by the terri-

tory manager affect the decisions of the network managers that, again, can be applied

by advisory or coercive policies and, in their turn, affect the decisions of the network

users. Therefore, the network users make their decisions by taking into account the so-

cial policies of the territory managers and the cost/incentive policies provided by the

infrastructure managers.

The main decisions of the proposed system, i.e. the deﬁnition of the path followed

by the logistic units, the transportation mode and the time instant in which they enter the

network, are taken by network users and this can be obtained as the solution of a speciﬁc

optimization problem. The considered objective function concerns the minimization of

some cost terms concerning the network users (travel costs, also including highway or

rail fares, deviations from due dates, and so on), possibly weighted in a different way

for each network user. In the considered optimization problem, the constraints include

the discrete-time state equations of nodes and links, as well as some other speciﬁc con-

straints. Note that the decisions taken by infrastructure managers and territory managers

can affect the optimization problem both in the objective function and in the constraints.

For instance, if the manager of a node/link applies different fares in different time slots,

this is considered in the problem objective function. Otherwise, if the territory manager

imposes a limit to the number of logistic units that can move in a certain area in a given

time slot, this is considered in the problem by adding a constraint.

The proposed model is very general and can refer to different real applications, by

adding speciﬁc constraints and/or decision variables. If a completely centralized system

is considered, a single large optimization problem must be solved. Since such a problem

generally has a nonlinear form, if real applications are considered, the problem dimen-

sions are probably too large to be solved with nonlinear solvers. For this reason, it could

be more reasonable to state different separate problems for each network user or for

groups of network users, in order to obtain smaller instances of the problem. Anyway,

in this case, it is necessary to model the interaction among the network users (either

in a competitive or in a cooperative environment) such that an overall solution can be

obtained by considering the single solutions that each of them has found by solving its

speciﬁc optimization problem. The present research activity is devoted to the analysis

of some real situations and the statement of ad-hoc optimization problems, in order to

evaluate the effectiveness of different management policies in logistic networks.

References

1. C. J. Vidal and M. Goetschalckx, “Strategic production-distribution models: a critical review

with emphasis on global supply chain models”, European Journal of Operational Research,

vol. 98 (1997).

2. M. Goetschalckx, C. J. Vidal, and K. Dogan, “Modeling and design of global logistic sys-

tems: a review of integrated strategic and tactical models and design algorithms”, European

Journal of Operational Research, vol. 143 (2002).

3. T. G. Crainic, “Long-haul freight transportation”, in R. W. Hall, editor, Handbook of Trans-

portation Science, Kluwer Academic Publishers (2003).

4. C. F. Daganzo, Logistics systems analysis, 4th edition, Springer (2005).

5. H. Pirkul, V. Jayaraman, “A multicommodity, multiplan, capacitated facility location prob-

lem: formulation and efﬁcient heuristic solution”, Computers and Operations Research, vol.

25, pp. 869-878 (1998).

6. M. S. Daskin and S. H. Owen, “Location models in transportation”, in R. W. Hall, editor,

Handbook of Transportation Science, Kluwer Academic Publishers (2003).

7. T. G. Crainic and G. Laporte, “Planning models for freight transportation”, European Journal

of Operational Research, vol. 98 (1997).

8. T. G. Crainic, “Network design in freight transportation”, European Journal of Operational

Research, vol. 122 (2000).

9. T. G. Crainic and J. Roy, “O. R. tools for tactical freight transportation planning”, European

Journal of Operational Research, vol. 33 (1988).

10. D. Kim, C. Barnhart, K. A. Ware, and G. Reinhardt, “Multimodal express package delivery:

a service network design application”, Transportation Science, vol. 33 (1999).

11. W. B. Powell, “A comparative review of alternative algorithms for the dynamic vehicle al-

location problem”, in B. L. Golden and A. A. Assad, editors, Vehicle Routing: Methods and

Studies, North-Holland (1988).

12. W. B. Powell, P. Jaillet, and A. Odoni, “Stochastic and dynamic networks and routing”, in

M. O. Ball, T. L. Magnanti, C. L. Monma, and G. L. Nemhauser, editors, Handbooks in

Operations Research and Management Science: Network Routing, North-Holland (1995).

13. W. B. Powell, B. Bouzaiene-Ayari, and H. P. Simao, “Dynamic models for freight trans-

portation”, in C. Barnhart and G. Laporte, editors, Handbooks in Operations Research and

Management Science: Transportation, North-Holland (2006).

14. M. Papageorgiou, “Dynamic modeling, assignment an route guidance in trafﬁc networks”,

Transportation Research B, vol. 28-2, pp. 279-293 (1990).

15. M. H. Lighthill and G. B. Whitham, “On kinematics waves II: a theory of trafﬁc ﬂow on

long, crowded roads”, Proceedings of the Royal Society of London series A, vol. 229, pp.

317-345 (1955).

16. P.I. Richards, “Shockwaves on the highway”, Operations Research, vol. 4, pp. 42-51 (1956).

17. D. R. Drew, Trafﬁc ﬂow theory and control, McGraw-Hill (1968).